运筹学,案例分析三：便民超市的网点布设问题
便利超市选址典型分析范例
12 X
解：从图中可以得出目的地的坐标
目的地
x, y
图书馆
6,7
东院食堂
2,5
C D座
10,5
E F座
10,3 28,20
x=∑x/n=28/4=7 y=∑y/n=20/4=5
因此,中心位置是(7,5),正好位于C座前的空地
假定下图描述的问题中运往各地商品数量不一样，而是 如下所示，则重心位置：
公寓：k 公寓东侧门口; l 大学生公寓城11号楼管理室．
淘汰法
淘汰法：考察所有备选方案的各项指标，将 不符合指标的方案排除，挑选出较优方案。 主要考虑：人流量、可行性。 资料来源：根据统计的人流量多少进行评分; 根据方案的可行性大小进行评分。 如下表、图:
人流量—可行性比较表
地点
abcdef ghi j kl
2、经过小组讨论，制定出选址所适宜的方法及一些主考因 素；
3、依次运用各类方法对挑选出的四个备选方案进行比较； 4、得出一个最佳方案； 5、项目总结。
若干地点：
西院：a 综合楼与天才小餐厅之间空地上; b 西院图书馆西侧5米处； c 西院食堂对过； d 体育馆内； e 原学工部；
东院：f 心园餐厅对过； g 东院食堂西侧； h 月牙报告厅附近； i D、E 座的北面教室 j 存车处到C座前空地；
四个备选方案人流量柱型图
3500
3000
2500
2000
1500
1000
500
0
1
2
3
4
析 素经门 选
选
注 ： 以 下 是 采 用 各 种 方 法 进
。营槛
时人
间口
、、
租学
金校 、政 面策 积、 等预 一期 系成
物流网点布局模型的建立及求解
物流运输与配送管理作业物流工程1001班100105113张露露物流网点布局模型的建立及求解物流网点是组织物流活动的基本条件。
由于受物资资源的分布、需求状况、运输条件和自然环境等因素的影响,不同的物流网络布局方案,其物流系统的运营效率和经济效益是不相同的,有时差别甚至很大。
如何设置物流网点,才能使物流费用最小,社会经济效益最佳,对客户的服务质量最好呢?对于多元多品种的物流网点布局问题,由于各个品种都要按照各自的优化方案选择中转点,因此同一用户可能需要同类不同品种的物资,这将分别从几个不同的网点进货,势必造成某些需求两不多的物资的运输工具的利用率降低、运输成本增大的现象。
为此,我们将各用户所需同类不同品种物资的进货相对集中。
希望从某一网点进货的数量应有一个最低的限额。
一，与网点相关的费用网点布局模型通常是以系统的总成本最低位目标函数。
建立模型时主要应该考虑一下几项费用：1)网点建设投资。
网点建设投资包括建筑物、设备和土地征用等费用。
2)网点内部的固定费用。
网点设置以后的人员工资、固定资产折旧以及行政支出等与经营状态无关的费用，称之为网点内部的固定费用，它与网点的位置无关。
3)网点经营费用。
经营费用是提高网点在经营的过程中发生的费用，如进出库费用、保管费用等，它是与经营状态直接相关的费用，即与网点中转量的大小有关。
4)运杂费。
运杂费是物流运输过程中所发生的费用，主要包括运价、途中换乘转装以及支垫物资等发生的费用，很明显，它与运输线，即与网点的位置有关。
物流系统的分析与设计是第三方物流服务或咨询中的一项重要内容,好的供应链管理是从物流系统分析与设计开始的。
物流网点布局方法研究综述在物流研究中,定量的系统分析和系统综合已经受到人们更多的重视,模型是开展这项工作的有效工具,也是开展这项工作的前提和基础。
二物流网点布局模型的约束条件1)资源点向外提供的资源量不超过其生产能力。
2)运达用户的物资等于它的需求。
连锁便利店配送线路优化课程设计范本
连锁便利店配送线路优化课程设计范本引言连锁便利店在城市中的数量逐渐增加，为了满足市民的购物需求，提高配送效率和准时性成为了连锁便利店管理者面临的重要问题。
本课程设计将介绍连锁便利店配送线路优化的方法和技术，旨在帮助学生理解和掌握如何使用运筹学和优化算法解决这一问题。
一、连锁便利店配送问题的定义和背景连锁便利店配送问题是指在满足客户需求的前提下，决定配送线路和顺序，以最小化成本和时间的问题。
在城市中，连锁便利店通常需要面对大量订单和客户，如何合理安排配送线路和减少配送员的行驶距离成为了管理者需要解决的重要问题。
传统的连锁便利店配送问题通常按照顺序逐个处理订单，往往导致配送线路不合理，时间成本高，配送员负担重。
因此，采用优化算法和运筹学方法对配送线路进行优化是提高连锁便利店配送效率的重要手段。
二、连锁便利店配送线路优化方法1. 数据收集与分析在进行连锁便利店配送线路优化前，需要对配送点的相关数据进行收集和分析。
包括订单数量、订单分布、配送点距离等信息。
通过对这些数据的综合分析，可以对配送线路进行初步规划和优化。
2. 车辆路径规划算法车辆路径规划算法是解决配送线路优化问题的核心方法之一。
常用的算法包括遗传算法、蚁群算法、模拟退火算法等。
这些算法通过优化车辆的路径和顺序，使得总体行驶距离最小化，达到减少时间和成本的目的。
3. 配送员工作时间管理除了优化车辆路径，合理安排配送员的工作时间也是提高连锁便利店配送效率的关键。
合理分配配送员的工作时间，避免不必要的等待和空闲，可以减少整体配送时间和成本。
4. 多车辆配送问题在实际情况中，连锁便利店通常有多个配送车辆。
如何合理安排多个车辆的配送线路，从而提高整体效率，是一个需要考虑的问题。
可以通过将问题转化为旅行商问题来解决，同时结合遗传算法等优化算法进行求解。
三、课程设计要求和评分标准本课程设计要求学生能够基于所学知识掌握连锁便利店配送线路优化的方法和技术，通过对实际情景的分析和建模，采用合适的优化算法解决问题。
连锁便利店配送线路优化课程设计范本
连锁便利店配送线路优化课程设计范本课程设计课程名称: 交通运输组织学设计题目: 联华连锁便利店配送线路优化设计学生姓名: 学号: 班级: 院系名称: 交通运输工程学院指导老师: 周骞、叶鸿、王佳年 1 月<交通运输组织学>课程设计课程名称: 交通运输组织学设计题目: 联华连锁便利店配送线路优化设计学生姓名:学号:班级:院系名称: 交通运输工程学院指导老师: 周骞、叶鸿、王佳长沙理工大学课程设计任务书交通运输工程学院交通运输专业班课程名称交通运输组织学题目联华连锁便利店配送线路优化设计学生姓名学号注:1、此任务书由指导老师填写。
如果不够,能够加页;2、此任务书最迟必须在课程设计开始前一周下达给学生;交通运输组织学课程设计指导书一、课程设计目的与要求1、课程设计目的<交通运输组织学>课程是交通运输本科专业的必修课, 是一门理论与实践结合紧密的核心课程。
本课程设计是在该门课程的课堂教学完成之后,为巩固课程涉及到的交通运输组织学方面的方法、理论及应用而开展的。
经过课程设计,使学生能够结合实际背景,应用已学理论,解决实际问题,从而培养学生资料查阅能力、绘图能力、理论联系实际的能力、系统解决问题的逻辑思维能力等,为毕业论文设计及今后从事相关工作打下基础。
2、课程设计要求本课程设计要求学生根据课程涉及的相关内容与方法,结合实际背景,系统解决交通运输组织实际问题。
从背景分析、提出问题、解决问题、主要结论等几个方面开展。
要求课程设计具有系统性、完整性、与课程相关性并具有一定的研究深度。
二、课程设计的依据与资料来源课程设计的依据:①交通运输部客货运组织与管理相关标准与规范②董千里。
交通运输组织学[M] 。
人民交通出版社,④李维斌。
公路运输组织学 [M] 。
人民交通出版社,⑤崔书堂,朱艳茹。
交通运输组织学[M]。
东南大学出版社,⑤戴彤焱。
运输组织学[M]。
机械工业出版社,资料来源:①指导教师提供相关资料;②实际调研收集资料;③相关书籍;④网络资料收集。
离散数学超市选址
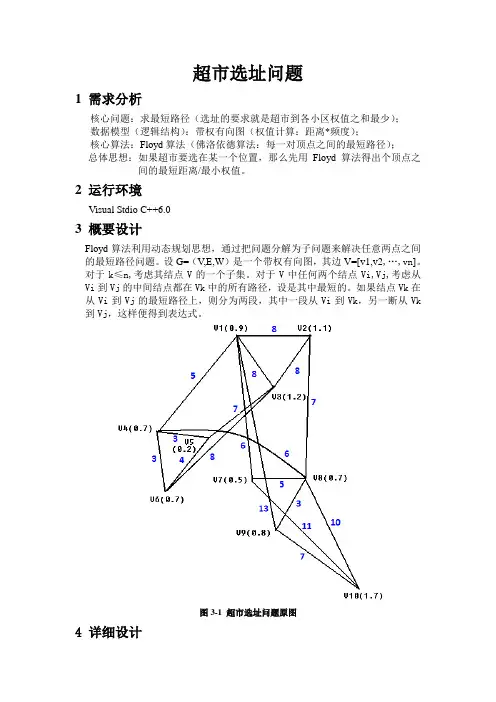
超市选址问题1 需求分析核心问题：求最短路径（选址的要求就是超市到各小区权值之和最少）；数据模型（逻辑结构）：带权有向图（权值计算：距离*频度）；核心算法：Floyd算法（佛洛依德算法：每一对顶点之间的最短路径）；总体思想：如果超市要选在某一个位置，那么先用Floyd算法得出个顶点之间的最短距离/最小权值。
2 运行环境Visual Stdio C++6.03 概要设计Floyd算法利用动态规划思想，通过把问题分解为子问题来解决任意两点之间的最短路径问题。
设G=（V,E,W）是一个带权有向图，其边V=[v1,v2,…,vn]。
对于k≤n,考虑其结点V的一个子集。
对于V中任何两个结点Vi,Vj,考虑从Vi到Vj的中间结点都在Vk中的所有路径，设是其中最短的。
如果结点Vk在从Vi到Vj的最短路径上，则分为两段，其中一段从Vi到Vk，另一断从Vk 到Vj，这样便得到表达式。
图3-1 超市选址问题原图4 详细设计让所有路径加上中间定点1，取A[i][j]与A[i][l] +A[l][j]中较小的值作A[i][j]的新值，完成后得到A（l），如此进行下去，当第k步完成后，A(k)[i][j]表示从i到且路径上的中间顶点的路径序号小于或等于k的最短路径长度。
当第n-1步完成后，得到A（n-1）, A（n-1）即所求结果。
A（n-1）[i][j]表示从i到j 且路径上的中点顶点的序号小于或等于n-1的最短路径长度，即A（n-1）[i][j]表示从i到j最短路径长度。
5调试分析有两个权值，各小区到超市的距离及小区的人数。
图的建立有很大的困难，经过分析这两个值可以合并为一个权值，从而便于分析和解决问题。
6 程序代码#include <string.h>#include <stdio.h>#include <time.h>#include "malloc.h"#include <iostream.h>#define TURE 1#define FALSE 0#define OK 1#define ERROR 0#define OVERFLOW -1#define INF 65535const int MAXVEX=100;typedef char Vextype;typedef struct{Vextype vexs[MAXVEX][MAXVEX];int adj[MAXVEX][MAXVEX];int dis[MAXVEX][MAXVEX];int f[MAXVEX];int n;int e;}Mgraph;void CreatMgraph(Mgraph *G){int i,j,k;printf("请输入小区个数:\n");scanf("%d",&(G->n));printf("请输入小区间的路径数:\n");scanf("%d",&(G->e));printf("请输入小区名称:\n");for(i=0;i<G->n;i++){printf("请输入第%d个小区名称:\n",i);scanf("%s",&G->vexs[i]);}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){G->adj[i][j]=0;G->dis[i][j]=0;G->f[i]=0;}for(k=0;k<G->e;k++){printf("请输入相通的两小区(输入格式:i,j):\n");scanf("%d,%d",&i,&j);printf("请输入相通两个小区间的距离(格式：dis)：\n");scanf("%d",&(G->dis[i][j]));G->adj[i][j]=1;G->adj[j][i]=1;G->dis[j][i]=G->dis[i][j];}for(k=0;k<G->n;k++){printf("请输入第%d个小区的人数:\n",k);scanf("%d",&(G->f[k]));}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){G->dis[i][j]*=G->f[i];if(G->adj[i][j]==0&&i!=j)G->dis[i][j]=INF;}}void Floyed(Mgraph *G){int A[MAXVEX][MAXVEX],path[MAXVEX][MAXVEX]; int i,j,k,pre;int count[MAXVEX];for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){A[i][j]=G->dis[i][j];path[i][j]=-1;count[i]=0;}for(k=0;k<G->n;k++){for(i=0;i<G->n;i++)for(j=0;j<G->n;j++)if(A[i][j]>(A[i][k]+A[k][j])){A[i][j]=A[i][k]+A[k][j];path[i][j]=k;}}cout<<endl<<"Floyed算法求解如下:"<<endl;for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){if(i!=j){cout<<" "<<i<<"->"<<j<<";";if(A[i][j]==INF){if(i!=j)cout<<"不存在路径"<<"\n"<<endl;}else{cout<<"路径长度为:"<<A[i][j]<<"\n";cout<<"路径为:"<<i<<" ";pre=path[i][j];while(pre!=-1){cout<<pre<<"\n";pre=path[pre][j];}cout<<j<<endl;}}}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++){if(A[i][j]==INF)count[i]=0;elsecount[i]=1;}for(i=0;i<G->n;i++)if(count[i]){for(j=0;j<G->n;j++)A[i][0]+=A[i][j];}for(i=0;i<G->n;i++){k=0;if(count[i])if(A[k][0]>A[i][0])k=i;}cout<<"超市的最佳地址为:"<<G->vexs[k]<<endl; }void main(){Mgraph *Gh=NULL;Gh=(Mgraph *)malloc(sizeof(Mgraph)); CreatMgraph(Gh);Floyed(Gh);}7 测试结果7.1 输入7.2 输出8 参考文献：[1].谭浩强编著《C语言程序设计》,清华大学出版社 .[2].严蔚敏编著《数据结构与算法分析》，清华大学出版社.9 课程总结本次题目是设计一个超市选址的问题，在实际生活中，非常实际的一个题目，有着很大的实际用途。
《运筹学》案例5 营业网点设置问题
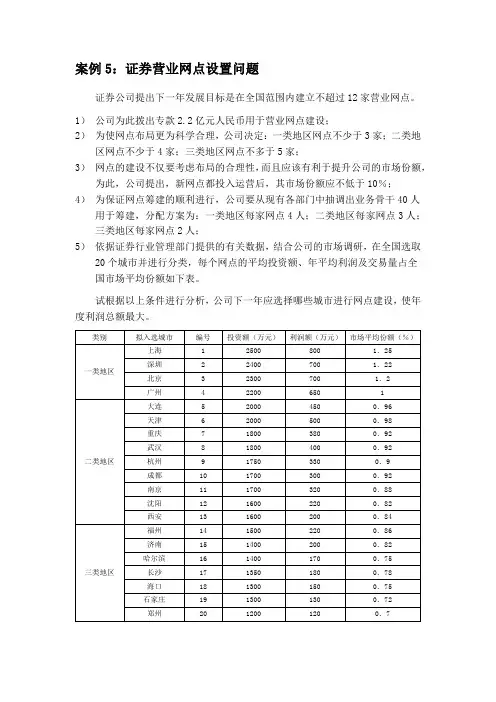
案例5：证券营业网点设置问题
证券公司提出下一年发展目标是在全国范围内建立不超过12家营业网点。
1）公司为此拨出专款2.2亿元人民币用于营业网点建设；
2）为使网点布局更为科学合理，公司决定：一类地区网点不少于3家；二类地区网点不少于4家；三类地区网点不多于5家；
3）网点的建设不仅要考虑布局的合理性，而且应该有利于提升公司的市场份额，为此，公司提出，新网点都投入运营后，其市场份额应不低于10％；
4）为保证网点筹建的顺利进行，公司要从现有各部门中抽调出业务骨干40人用于筹建，分配方案为：一类地区每家网点4人；二类地区每家网点3人；
三类地区每家网点2人；
5）依据证券行业管理部门提供的有关数据，结合公司的市场调研，在全国选取20个城市并进行分类，每个网点的平均投资额、年平均利润及交易量占全国市场平均份额如下表。
试根据以上条件进行分析，公司下一年应选择哪些城市进行网点建设，使年度利润总额最大。
运筹学上机实验-超市网点设计
运筹学上机实验（二）题目：便民超市的网点布设学号：2220113731姓名：谭传芳专业：数学与应用数学一．实验内容与要求南平市规划在其远郊建一卫星城镇，下设20个街区，如下图。
各街区居民数预期为1、4、9、13、17、20各12000人；2、3、5、8、11、14、19各14000人；6、7、10、12、15、16、18各15000人。
便民超市准备在上述街区进行布点。
根据方便就近的原则，在某一街区设点，该点将服务于该街区及相邻街区。
例如在编号为3的街区设一超市点，它服务的街区为1、2、3、4、6。
由于受经费限制，便民超市将在上述20个街区内先设两个点，请提供你的建议：在哪两个街区设点，使其服务范围的居民人数为最多。
二．实验原理根据图示及材料可以总结出以下表格：2、设街区编号为Xi,在第i 个街区设点能服务到的人数为a i令 Xi=1时，表示在第i 街区设点；Xi=0时，表示在第i 街区不设点{10,2..m ax )20,193,2,1(01201201或目标函数：个街区不设点，在第个街区设点，在第==⎩⎨⎧=⋯⋯==∑∑==i i i i ii ii x x a t s x aZ i i i x三．实验步骤：数学模型上面已经建立，下面利用运筹学整数规划模型求解1、打开运筹学软件，点击整数规划，选择纯整数规划，单击菜单中的“新建”2、在变量个数中输入：20，在约束条件中输入：21，选择Max ，然后单击确定3、在目标函数中变量X1，X2，……X19，X20所对应的系数分别填入：4、共设21个约束条件(j=21)，前20个约束条件是为了保证Xi=0或1，第21个约束条件是为了保证从20个街区中选2个。
（1）在约束条件j （j=1、2、3…18、19、20）中：除了变量Xi （当i=j 时）的系数填“1”，其余变量的系数都填“0”，符号都选择“≤”，b 的值都为“1”；（2）在约束条件j （j=21）中：所有变量Xi 的系数都填“1”，符号选择“=”，b 的值为“2”单击“确定”，数据输出如下结果表明：在街区6和14设点时，便民超市可以服务的居民人数最多，预期最多服务人数为208000人。
奥运会临时超市网点设计
A题：奥运会临时超市网点设计摘要对于问卷所提供的数据，用ACCESS和SPSS统计和制表，得出同一人群的不同的乘车分布表、餐饮分布表、消费额分布表，并作出相应分布的直方图。
从直方图可以形象地看出，乘车除私车人数较少外，其余乘车方式基本均衡，吃西餐比吃中餐人少，尤其是年龄段2的人群。
用餐和出行视为两个不同时间段，分别就每个时间段进行计算。
用餐和出行均采用最短路径，然后列出具体路径表，再由此表和已统计出的规律计算经过每个商区人数，然后把用餐和出行计算出的人数相加即得通过该商区人数，也即为通过该商区的人数，该人数除以总人数得人流量，最后绘制出人流量分布表。
根据第一二问的结果，并根据人购物欲望值与商区提供的效用值对应，大MS和小MS在每个商区所提供的效用是不同的，视商区的人流量而定，人流量越大所提供的效用越大。
运用著名的经济学中的生产函数的思想：柯布.道格拉斯生产函数理论，建立起商区效用产出与各商区的大、小MS个数的关系模型。
根据生产函数的产出均衡条件，得出各商区大、小MS的数量近似分布。
根据最后的结果分析总结出经济可行的MS布局方案。
关键字：个人倾向，生产函数，边际效益，效用函数。
一、问题重述2022年北京奥运会中，为了满足观众、游客、工作人员等的购物须求，要在比赛主场馆的周边地区建设临时商业网点，称为迷你超市（MS）网，主要经营食品、奥运纪念品等。
设置时要满足三个基本要求：满足奥运会期间的购物需求、分布基本均衡和商业上盈利。
图1和图2给出了相应的信息在规定的20个商区内设计MS网点。
图3是预演运动的运动场，从问卷调查中，可以得到人流量的归律。
问题1 根据调查数据，找到观众在出行、用餐和购物等方面的归律。
问题2 在奥运期间每位观众每天平均出行两次，并且采用最短路径，算出20个商区的人流量分布。
问题3 要求满足三个基本要求，得出20个商区内MS网点的设计方案。
并且阐明其方法的科学性，是否符合实际。
二、问题分析题1需要找出观众在出行、用餐、购物等方面的规律，附录中给出了某体育场馆的相关调查数据，通过对调查结果的分析发现三次调查的结果基本相似，于是采取按人数求加权平均值。
某某超市物流系统布置诊断分析与优化分析方案
某某大学乐来得超市物流系统布置诊断分析与优化学院专业小组姓名及学号某某大学乐来得超市物流系统布置诊断分析与优化某某大学学生公寓西面、体育场对面的乐来得超市，属于小型生活便利超市，营业时间6:30-23:00之间，主要售卖学生日常用品：方便食品、生活用品等。
本小组以乐来得超市为物流系统，进行了为期三周的实地调研，通过问卷调查以及实地数据记录，对该超市进行了物流系统布置诊断分析与优化。
所谓物流系统是指在一定的时间和空间里，由所需输送的物料和包括有关设备、输送工具、仓储设备、人员以及通信联系等若干相互制约的动态要素构成的具有特定功能的有机整体。
超市物流系统一般系统一样，具有输入、转换及输出三大功能，乐来得超市输入的是“未经服务的顾客”，输出的是“被服务过的顾客”，转换就是“购物及结账”的过程。
以下是超市的简要平面布局图 < 图1 ）、超市通过人数统计表以及小组调查问卷 <样卷）：图1乐来得超市平面布局图II打炉靈库房/后勤处*未购物的同学+购物的同学奶茶超市通过人数统计表时间段前门岀数周一后门岀数实际结账人数前门岀数周二后门岀数实际结账人数前门岀数周三后门岀数实际结账人数前门岀数周四后门岀数实际结账人数前门岀数周五后门岀数实际结账人数前门岀数周六后门岀数实际结账人数前门岀数周日后门岀数实际结账人数7:40-8:00 522 13 122 589 3 150 467 6 182 493 21 174 512 17 132 87 25 32 55 12 33 第9:40-10:00 319 258 153 224 208 103 218 211 110 196 230 99 216 186 83 93 102 44 65 45 15 12:00-12:20 83 142 84 102 344 67 98 314 178 73 290 82 83 252 98 24 121 22 24 32 19 周15:50-16:10 159 398 131 125 369 89 153 403 85 193 382 102 153 406 142 25 35 13 15 32 21 17:50-18:10 124 199 132 142 102 73 176 78 84 153 142 141 163 131 124 32 46 24 42 64 25 7:40-8:00 594 13 88 493 19 153 482 2 153 533 14 132 482 19 83 63 23 18 33 32 12 第9:40-10:00 204 183 115 183 242 102 212 231 103 184 193 93 220 204 159 48 84 42 73 82 42 12:00-12:20 87 174 95 74 329 102 80 321 168 83 313 124 102 311 123 25 69 38 20 73 21 周15:50-16:10 166 351 146 142 354 142 172 329 133 163 383 142 153 363 89 42 102 25 62 111 53 17:50-18:10 122 188 139 153 142 122 152 93 79 183 124 129 153 163 129 34 42 24 82 93 52 7:40-8:00 583 12 89 513 11 102 456 5 168 514 16 83 482 15 131 69 28 22 62 14 14 第9:40-10:00 214 184 104 215 189 110 213 219 101 221 199 87 218 199 99 39 68 25 29 58 29 12:00-12:20 93 382 83 88 420 89 93 329 162 93 329 79 152 399 88 35 45 14 35 42 23 周15:50-16:10 162 385 134 124 382 102 182 392 106 192 329 93 194 310 105 73 83 25 82 52 34 17:50-18:10 142 183 129 185 183 93 143 123 124 193 152 124 142 182 123 102 93 83 92 104 84 注：1、统计的主要是上下课的高峰人数，比较有典型性2、前门岀数加后门岀数为经过的总人数某某大学乐来得超市的调查问卷尊敬的朋友，首先感谢您在百忙之中协助我们小组完成关于乐来得超市物流系 统规划方面的问卷调查。
连锁超市网点铺设方案
连锁超市网点铺设方案1. 引言连锁超市在现代都市生活中扮演着重要角色。
为了满足人们对方便、快捷购物的需求，连锁超市需要在合适的位置建立网点，以便顾客能够快速到达并享受购物体验。
本文将介绍连锁超市网点铺设的方案，包括选址考虑因素和实施步骤。
2. 选址考虑因素在选择连锁超市网点的位置时，需要考虑一系列因素，以确保网点能够获得良好的流量和可持续的经营：2.1 人口密度和消费能力选择人口密度较高且消费能力较强的地区是连锁超市铺设网点的首要因素。
人口密度高意味着潜在顾客数量多，消费能力强则能保证顾客的购买力。
2.2 竞争对手分布在选址时需要考虑竞争对手的分布情况。
选择人口密度高但竞争对手较少的地区，能够帮助连锁超市获得更大的市场份额和利润。
2.3 交通便利性网点应选择交通便利的地点，方便顾客到达。
靠近主干道、公交车站或地铁站的位置通常是较理想的选址。
2.4 周边设施和配套服务周边设施和配套服务的完善程度也是选址的重要考虑因素。
例如，选择附近有学校、办公楼和居民区的地方能够为网点带来更多的顾客流量。
3. 实施步骤3.1 市场调研在确定连锁超市网点铺设方案之前，需要进行市场调研。
市场调研可以帮助连锁超市了解潜在顾客的需求和购物习惯，以及竞争对手的存在和策略。
通过市场调研，可以更好地了解当前市场情况，为选址做出明智的决策。
3.2 选址分析根据市场调研的结果，连锁超市可以开始进行选址分析。
这一步骤需要综合考虑前述的选址考虑因素，对不同地点进行评估和比较。
利用地理信息系统（GIS）和统计数据可以帮助连锁超市进行选址分析。
3.3 选址决策在选址分析的基础上，连锁超市可以进行选址决策。
这一步骤需要综合所有因素，并权衡不同选址地点的优缺点。
选址决策需要综合考虑市场需求、竞争对手、交通便利性和周边配套服务等因素。
3.4 设计和建设选址决策确定后，连锁超市可以开始设计和建设新的网点。
设计和建设包括选择适当的建筑物或商业空间，设计合理的布局和展示区域，以及配置适当的设备和货架。
超市设施布置课程设计
超市设施布置课程设计一、教学目标本课程旨在让学生了解和掌握超市设施布置的基本知识和技能，培养学生对超市布局和设计的审美能力，提高学生对商业空间规划的认识。
知识目标：使学生了解超市的发展历程、各类设施的布置原则和方法，以及超市布局对消费者行为的影响。
技能目标：培养学生能够独立完成超市设施布置方案的设计，提高学生的创新能力和实践能力。
情感态度价值观目标：培养学生对超市设施布置工作的热爱，树立正确的商业道德观念，提高学生对社会零售业的认识。
二、教学内容本课程的教学内容主要包括超市设施布置的基本概念、设计原则、各类设施的布置方法，以及超市布局的实践案例。
1.超市设施布置的基本概念：介绍超市的发展历程、定义及其功能。
2.设计原则：讲解超市设施布置的设计原则，如实用性、美观性、安全性等。
3.各类设施的布置方法：详细介绍货架、收银台、休息区等超市设施的布置方法。
4.超市布局的实践案例：分析国内外典型的超市布局案例，使学生能够更好地理解和应用所学知识。
三、教学方法为了提高教学效果，本课程将采用多种教学方法相结合的方式进行教学。
1.讲授法：讲解超市设施布置的基本概念、设计原则和布置方法。
2.案例分析法：分析国内外典型的超市布局案例，提高学生的实践能力。
3.讨论法：学生进行小组讨论，培养学生的团队协作能力和批判性思维。
4.实验法：安排学生进行超市设施布置的实践操作，锻炼学生的动手能力。
四、教学资源为了支持教学内容和教学方法的实施，本课程将准备以下教学资源：1.教材：选用国内权威出版的《超市设施布置》教材，为学生提供系统的理论知识。
2.参考书：推荐学生阅读相关领域的经典著作，拓宽知识面。
3.多媒体资料：收集相关的视频、图片等多媒体资料，丰富教学手段。
4.实验设备：准备实体超市设施，为学生提供实践操作的机会。
五、教学评估本课程的评估方式包括平时表现、作业、考试等方面，以全面、客观、公正地评价学生的学习成果。
1.平时表现：评估学生在课堂上的参与度、提问回答等情况，以考察学生的学习态度和积极性。
生活中的运筹学案例
生活中的运筹学案例生活中的运筹学案例无处不在，它们展现了运筹学在实际生活中的应用和重要性。
运筹学是一门研究如何有效地组织和管理资源，以最大化效益的学科。
通过分析、建模和优化，运筹学可以帮助人们在生活中做出更加明智的决策，提高效率，节约资源，降低成本，提高生活质量。
下面我们将通过几个生活中的案例来看看运筹学是如何应用的。
首先，我们可以看看购物中的运筹学。
在购物过程中，我们需要考虑如何在有限的预算下购买最多的商品。
这就涉及到了“多重背包问题”，即在有限的背包容量下，如何选择商品来使得总价值最大化。
运筹学可以帮助我们建立数学模型，通过优化算法来解决这个问题，从而使我们在购物时可以更加理性地选择商品，最大化利益。
其次，生活中的旅行也是一个充满运筹学的场景。
在旅行中，我们需要考虑如何安排行程、选择交通工具和酒店，以及如何合理安排时间和预算。
这就涉及到了“旅行商问题”和“背包问题”。
运筹学可以帮助我们制定最佳的旅行计划，通过优化算法来确定最短的旅行路线和最合适的行程安排，使得旅行更加高效和愉快。
另外，生活中的排队问题也是一个典型的运筹学案例。
在超市、银行、医院等场所，我们经常需要排队等候。
如何合理安排队伍，减少等待时间，提高服务效率，是一个重要的问题。
运筹学可以帮助我们通过排队理论和优化算法来设计更加合理的排队系统，从而提高服务质量和顾客满意度。
最后，生活中的日常安排也离不开运筹学的帮助。
比如，如何合理安排工作和学习时间，如何有效规划饮食和锻炼计划，如何管理个人财务和投资等等，都可以通过运筹学的方法来进行优化和改进，使得生活更加有序和高效。
总之，生活中的运筹学案例无处不在，它们展现了运筹学在实际生活中的应用和重要性。
通过分析、建模和优化，运筹学可以帮助人们在生活中做出更加明智的决策，提高效率，节约资源，降低成本，提高生活质量。
希望大家能够在日常生活中更加关注和运用运筹学的方法，使得生活更加美好。
运筹学在服务设施布局规划中的应用
运筹学在服务设施布局规划中的应用运筹学是一门综合运用数学、经济学和工程学等学科知识来研究和解决实际问题的学科。
在现代社会，随着服务业的快速发展，服务设施布局规划成为了一个重要的问题。
运筹学的方法和技术可以帮助决策者合理布局服务设施，提高服务效率，降低成本。
本文将介绍运筹学在服务设施布局规划中的应用。
一、问题描述在服务设施布局规划中，决策者需要考虑多个因素，比如服务范围、设施容量、运输成本、客户需求等等。
为了解决这个问题，运筹学提供了一种优化模型，可以帮助决策者在满足各种约束条件下找到最优解。
二、数学模型运筹学将服务设施的布局问题抽象成数学模型。
以某快递公司为例，假设有n个城市需要布设快递中心，每个城市的快递量与之对应的运输成本不同。
决策者的目标是要找到一种布设方案，使得运输成本最低。
为了解决这个问题，可以使用整数规划方法建立数学模型。
假设x(i,j)表示城市i是否建立快递中心，y(i,j)表示城市i的快递是否运到城市j。
则目标函数可以表示为：Minimize ∑(i,j) c(i,j) * y(i, j)其中，c(i,j)表示从城市i到城市j的运输成本。
约束条件包括：∑(j) y(i, j) = x(i)，表示城市i只能有一个快递中心。
∑(i) y(i, j) >= d(j)，表示城市j的快递需求必须满足。
x(i)和y(i, j)的取值为0或1。
通过求解这个整数规划模型，可以得到最优的快递中心布局方案，从而达到降低运输成本的目的。
三、实例分析为了更好地说明运筹学在服务设施布局规划中的应用，我们以某连锁超市的门店布局问题为例进行实例分析。
假设该连锁超市有n个潜在门店选址点，需要从这些选址点中选取一部分作为实际门店开设点。
决策者的目标是要使得整个区域的服务范围最大化。
为了解决这个问题，可以使用覆盖模型建立数学模型。
假设x(i)表示选址点i是否开设门店，y(j)表示点j是否处于某门店的服务范围内。
（强烈推荐）基于SLP方法进行超市设施规划__毕业论文
（强烈推荐）基于SLP方法进行超市设施规划__毕业论文物流设施布置与设计论文题目：物美超市设施布置与设计目录1 选题背景 (2)2超市布局设计的意义 (2)3 基于SLP 的超市总体布局的步骤 (2)3.1 准备原始资料 (2)3.2 分析物流-作业单位的相互关系 (2)3.3 物流-作业单位 (2)3.4 分析评价各个方案，选出最优方案。
(3)4 步骤实施 (4)4.1 基于销售区之间的联系分析物流-作业单位的相互关系 (4) 4.1.2 根据测量数据作出从至表 (6)4.1.3 根据从至表作出人流排序表 (7)4.2 根据上面分析作出各销售区人流相关表 (7)4.3 基于销售区之间的联系分析非物流-作业单位的相互关系 (8) 4.3.1 非物流关系评级主要由下述理由确定： (8)4.3.2 分析影响销售区之间联系的因素 (8)4.3.3 通过上网搜集的资料，得出以下销售区之间的联系 (8) 4.4 基于上述的分析作出各销售区非物流相关 (9)4.5 作出各销售区综合相互关系表： (9)4.5.1 作综合相互关系表的要求 (9)4.5.2 根据上述要求得出综合相互关系图 (9)4.6 Tompkins关系表技术生成平面布置图 (10)4.6.1 关系工作表 (10)4.6.2 根据关系工作表作出无面积拼块图 (11)4.6.2.1 无面积拼块图的要求 (11)4.6.2.2 得出方案 (11)4.6.3对这些方案，我们可以作一个好坏评级 (12)4.6.3.1评价方法 (12)4.6.3.2 评价结果 (13)4.7 选取方案作出面积图 (13)4.7.1 面积图主要考虑两个问题： (13)4.7.2 根据原来各销售区的面积，各区的长宽可以适当改变，但其面积只可以稍微增加或减少 (13)4.7.3 如下图，为超市平面图 (13)4.7.4 根据拼块图和各销售区摆放及通道设计原则、面积要求得出的各销售区的布局图，命名为一楼改进方案1，方案2。
全国高等学校数学建模大赛典型案例-奥运会临时超市网点设计方案
奥运会临时超市网点设计方案摘要：本文针对2008年奥运会期间，为了能够满足观众、游客、工作人员等在奥运会期间的购物需求的问题，运用运筹学理论和统计分析方法，建立了整数线性规划模型，该模型最大的优点就在于基于现实，且分析时充分利用了各种科学理论知识进行分析计算，例如统计学、图论、概率的随机性、整数规划模型等进行了分析归纳推理，利用了各种软件例如Excel、Access等对数据进行了系统的处理，又利用了C语言，MATLAB等工具对数据进行了精确计算。
所涉及知识面较广，科学分析严密，对现实的考虑分析周到严密，所以就得到了一个具有科学性和实际可行性的整数线性规划模型，在许多城市规划模型中能够很好的使用。
关键词：迷你超市（Mini Supermarket, 记做MS）、人流量、最大消费额。
1．问题的提出：2008年北京奥运会的建设工作已经进入全面设计和实施阶段。
奥运会期间，在比赛主场馆的周边地区需要建设由小型商亭构建的临时商业网点，称为MS网，以满足观众、游客、工作人员等在奥运会期间的购物需求，主要经营食品、奥运纪念品、旅游用品、文体用品和小日用品等。
在比赛主场馆周边地区设置的这种MS，在地点、大小类型和总量方面有三个基本要求：满足奥运会期间的购物需求、分布基本均衡和商业上赢利。
在真实地图的简化图中仅保留了与本问题有关的地区及相关部分：道路（白色为人行道）、公交车站、地铁站、出租车站、私车停车场、餐饮部门等,其中标有A1-A10、B1-B6、C1-C4的黄色区域是规定的设计MS网点的20个商区。
为了得到人流量的规律，一个可供选择的方法，是在已经建设好的某运动场通过对预演的运动会的问卷调查，了解观众（购物主体）的出行和用餐的需求方式和购物欲望。
假设我们在某运动场举办了三次运动会，并通过对观众的问卷调查采集了相关数据。
根据给出的问卷调查数据，找出观众在出行、用餐和购物等方面所反映的规律；假定奥运会期间（指某一天）每位观众平均出行两次，并且出行均采取最短路径。
关于A超市服务网点布局方案优化设计
关于A连锁超市服务网点布局设计优化方案随着物流行业的发展, 物流服务网点的地位也不断突显, 而其选址又是物流服务网点所有工作的首要环节, 物流服务网点的位置恰当与否, 直接关系到整个配送的效率、物流成本以及顾客服务水平, 会对企业的运营产生重要影响。
较佳的物流服务网点选址方案是使商品通过物流服务网点的汇集、中转、分发, 直至输送到需求点的全过程的效益最好。
由于物流服务网点拥有众多建筑物以及固定机械设备, 因此规划得合理与否, 将对物流服务网点的设计、施工与应用, 对其作业质量、安全、作业效率和保证供应, 对节省投资和运营费用等, 都会产生直接和深远的影响。
一、公司简介（一）成立及发展A超市股份有限公司是扬州市的一家小型连锁超市，成立于1997年1月。
公司以“挑战极限，追求卓越”为企业精神，以“低成本、低投入、高效益、高产出”为经营原则，以特许加盟为经营特色，形成了以标准超市、大卖场、便利店为主营业态，以现代化物流和信息化管理为核心技术，以开拓扬州市场、乃至江苏省为目标的经营格局。
至2012年底，拥有连锁门店5家，网点遍布扬州市。
公司坚持发展中调整，调整中提升，以发展，转型，提升为工作指针，通过快速发展，积极转型，有效提升，实现预期的经济目标，为超商事业的发展作出应有贡献。
（二）经营范围该公司主营业务为连锁超市，经营范围为：服装鞋帽，服饰系列配套商品，日用百货，工艺美术品，五金交电，文教用品，中西餐饮，仓储运输，经营进出口业务，建材、装潢材料，超市管理，食品，常用药品，粮食及其制品，连锁加盟，副食品，收购水产品、蔬菜、水果，烟，酒，等。
（三）企业文化该超市有限责任公司，是以经营各类家居用品、文体用品、家电、针织品、服饰类；各类休闲、饮料、烟酒等商品批发、零售业务为主，以统一形象、统一标志、统一经营、统一管理为发展方向的零售连锁经营企业。
经营目标：通过连锁、规模经营，在市场占有一席之地。
用人观念：能者上、平者让、庸者下；落实培训、推行本土化经营特色：满足顾客的需求。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
运筹学案例分析报告
—便民超市的网点布设
班级：1516122
组号：6
姓名、学号
（组长、分工）：吴锴楠、建立数学模型
（组员、分工）：张灿龙、编写lingo程序
（组员、分工）：游泽锋、编写报告
一、案例描述
南平市规划在其远郊建一卫星城镇，下设20个街区，如图所示。
各街区居民数预期为1、4、9、13、17、20各12000人；2、3、5、8、11、14、19各14000人；6、7、10、12、15、16、18各15000人。
便民超市准备在上述街区进行布点。
根据方便就近的原则，在某一街区设点，该点将服务于该街区及相邻街区。
例如在编号为3的街区设一超市点，它服务的街区为1、2、3、4、6。
由于受到经费限制，便民超市将在上述20个街区内先设两个点。
请提供你的建议：在哪两个街区设点，使其服务范围的居民人数为最多。
二、案例中关键因素及其关系分析
1、在某一街区设点，该点将服务于该街区及相邻街区（当街区i或街区i的相邻街区设网点时，街区i受服务）。
当街区i受服务时，受服务居民人数增加ai，各街区
3、要求两个街区设点，使其服务范围的居民人数为最多
三、模型构建
1、决策变量设置
同时每一个街区有受服务和不收服务两种状态,故每个街区可以设置一个0-1变量：
因为每一个街区有设为网点和不设为网点两种状态,故每个街区可以设置一个0-1变量：
2、目标函数的确定：
街区i受服务，受服务居民人数增加ai，该案例目标为使服务范围的居民人数为最多，故目标函数可设为：
3、约束条件的确定
i)便民超市将在20个街区内设两个点，由此可确定一个约束条件：
ii）当街区i和它的相邻街区中设有一个或两个网点时，街区i受服务，即街区i和它的相邻街区对应的各个yi加起来为1或2，此时xi应为1；当街区i和它的相邻街区中没有网点时，街区i不受服务，即街区i和它的相邻街区对应的各个yi加起来为0，此时xi应为0；用[m]表示不超过m的最大整数，由此可确定20个约束条件：
4、数学模型构建
综上，该案例的整个数学模型如下：
s.t.
四、模型求解
1、求解工具及适应性分析
求解工具：Lingo11。
2、求解过程分析
把上面的方程的用lingo写出来，然后在设置为全局最优解，最后运行求解，我们的编程程序如下：
max=x1*12+x2*14+x3*14+x4*12+x5*14+x6*15+x7*15+x8*14+x9*12+x10*15+x11*14+x1 2*15+x13*12+x14*14+x15*15+x16*15+x17*12+x18*15+x19*14+x20*12;
y1+y2+y3+y4+y5+y6+y7+y8+y9+y10+y11+y12+y13+y14+y15+y16+y17+y18+y19+y20=2; x1=@floor((y1+y2+y3+y4+1)/2);
x2=@floor((y1+y2+y3+y6+y9+y11+1)/2);
x3=@floor((y1+y2+y3+y4+y6+1)/2);
x4=@floor((y1+y4+y3+y6+y5+1)/2);
x5=@floor((y4+y5+y7+y8+1)/2);
x6=@floor((y2+y3+y4+y6+y7+y11+y13+1)/2);
x7=@floor((y5+y6+y7+y8+y13+y15+1)/2);
x8=@floor((y5+y7+y8+y15+1)/2);
x9=@floor((y2+y9+y10+y11+1)/2);
x10=@floor((y9+y10+y11+y12+y17+1)/2);
x11=@floor((y2+y6+y9+y10+y11+y12+y13+y14+1)/2);
x12=@floor((y10+y11+y12+y14+y18+y17+1)/2);
x13=@floor((y6+y7+y11+y13+y14+y15+1)/2);
x14=@floor((y11+y12+y13+y14+y15+y16+y18+y20+1)/2);
x15=@floor((y7+y8+y13+y14+y15+y16+1)/2);
x16=@floor((y14+y15+y16+y20+1)/2);
x17=@floor((y10+y12+y17+y18+y19+1)/2);
x18=@floor((y12+y14+y17+y18+y19+y20+1)/2);
x19=@floor((y17+y18+y19+y20+1)/2);
x20=@floor((y14+y16+y18+y19+y20+1)/2);
3、求解结果及分析
经过运行得到的结果为：182，即服务范围内居民人数最多为182*10^3；
其中y6=y14=1,
y1=y2=y3=y4=y5=y7=y8=y9=y10=y11=y12=y13=y15=y16y=17=y18=y19=y20=0
即在第6和第14街区设置网点；
其中x2=x3=x4=x6=x7=x11=x12=x13=x14=x15=x16=x18=x20=1,
x1=x5=x8=x9=x10=x17=x19=0
即第2、3、4、6、7、11、12、13、14、15、16、18、20街区的居民受服务，第1、5、8、9、10、17、19街区的居民不受服务。
五、结论
1、决策效果（结果）的评价
通过严格的案例分析以及我们组全体成员的研究讨论、反思修正以及lingo软件的精密的计算，本案例得出最佳决策结果，在第6和第14街区设置网点，使服务范围的居民人数为最多，为182*10^3.
2、遇到的问题及解决方法
刚开始的时候我们遇到的第一个问题就是如何把xi和yi联系起来，使得满足当街区i 和它的相邻街区中设有一个或两个网点时，即街区i和它的相邻街区对应的各个yi有
为1的时候xi=1，当街区i和它的相邻街区中没有网点时，即街区i和它的相邻街区对应的各个yi都为0时，xi=0；于是我们想把目标规划的的最大化转变为最小化，利用yi<M*xi把xi和yi联系起来，于是我们利用三个服务人数中的ai，减去他们三个中的最大值作为新的ai，这样就能求原规划的最大值就是求新规划的最小值了，但是后来我们经过运算发现得出来的结果是错误的，我们重新讨论了一下，发现那样做的话，新的目标规划里的ai的比例会与原来ai的比例不相同，而我们也没有找出能使得到新的ai比例相同的方法，所以我们最终放弃了这种转变规划的方法。
接着我们经过讨论得出了另外一种方法，就是把每个xi能服务到的所能对应的选点列出来相加，而得到下面原始的目标函数：
Max
z=(y1+y2+y3+y4+1)/2]*x1*12+[(y1+y2+y3+y6+y9+y11+1)/2]*x2*14+[(y1+y2+y3+y4+ y6+1)/2]*x3*14+[(y1+y4+y3+y6+y5+1)/2]*x4*12+[(y4+y5+y7+y8+1)/2]*x5*14+[(y2 +y3+y4+y6+y7+y11+y13+1)/2]*x6*15+[(y5+y6+y7+y8+y13+y15+1)/2]*x7*15+[(y5+y7 +y8+y15+1)/2]*x8*14+[(y2+y9+y10+y11+1)/2]*x9*12+[(y9+y10+y11+y12+y17+1)/2] *x10*15+[(y2+y6+y9+y10+y11+12+13+14+1)/2]*x11*14+[(y10+y11+y12+y14+y18+y17 +1)/2]*x12*15+[(y6+y7+y11+y13+y14+y15+1)/2]*x13*12+[(y11+y12+y13+y14+y15+y 16+y18+y20+1)/2]*x14*14+[(y7+y8+y13+y14+y15+y16+1)/2]*x15*15+[(y14+y15+y16 +y20+1)/2]*x16*15+[(y10+y12+y17+y18+y19+1)/2]*x17*12+[(y12+y14+y17+y18+y19 +y20+1)/2]*x18*15+[(y17+y18+y19+y20+1)/2]*x19*14+[(y14+y16+y18+y19+y20+1)/ 2]*x20*12，经运算后我们得到了两个选点y6和y14，对比图形发现也较为合理，但是经过我们认真检查，发现得出来的xi都是1，然后我们再看回规划发现此时原规划里的xi是不受约束的，为了得到最大值，它会都取1 。
于是，我们再次改进得到新的目标规划如上文。
最后运算得到的结果还是选点y6和y14，各个xi的值也都正确。