平差大全---指导与习题

合集下载

平差习题集

1. 误差来源，测量平差的任务，多余观测的目的。

2. 试用公式说明方差协方差阵与协因数阵之间的关系？协因数阵与权阵之间的关系？在什么情况下它们为对角矩阵？若协因数阵为单位阵表示什么意思？ 3. 已知随机变量y 、z 都是观测值L=[L1、L2、L3]T 的函数，函数关系如下：3162101733241L L L z L L L y +-=++=，已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=420231012LLQ ，证明y 、z 间互不相关。

4. 已知间接平差的模型为V=BX-L ，已知观测值的中误差为Q LL ，试推导Q VV 。

5. 已知独立观测值L 1,L 2的中误差为σ1和σ2，试求下列函数的中误差：（1）122X L L =- （2）211212Y L L L =+6. 某平差问题有15个同精度观测值，必要观测数为8，现选取8个参数，且参数之间有2个限制条件。

若按附有限制条件的条件平差法进行平差，应列出多少个条件方程和限制条件方程？由其组成的法方程有几个？7. 在相同条件下，观测两个角度∠A=30︒00'00"，∠B=75︒00'00"，设对∠A 观测6个测回的权为1，问观测∠B 9个测回的权为多少？8. 在相同观测条件下，应用水准测量测定点A —B —C —D 之间的高差，设路线长度分别为S 1=2km ，S 2=4km ，S 3=6km ，令12km 的高差观测值权为单位权观测，设每公里观测高差中误差为σ，试求各段观测高差之权及单位权中误差。

9. 取一长度为d 的直线之丈量结果的权为1，则长度为D 的直线之丈量结果的权为多少？若长度为D 的直线丈量了n 次，则其算术平均值的权为多少？。

10. 已知一水准网如下图，其中A 、B 为已知点，观测了8段高差，若设E 点高程的平差值与B 、E 之间高差的平差值为未知参数21ˆˆX X 、，按附有限制条件的条件平差法（概括平差法）进行平差时，必要观测个数为，多余观测个数为，一般条件方程个数为，限制条件方程个数为C11. 在已知水准点A 、B （其搞成无误差）间布设设水准线路，如图所示。

测量平差所有习题

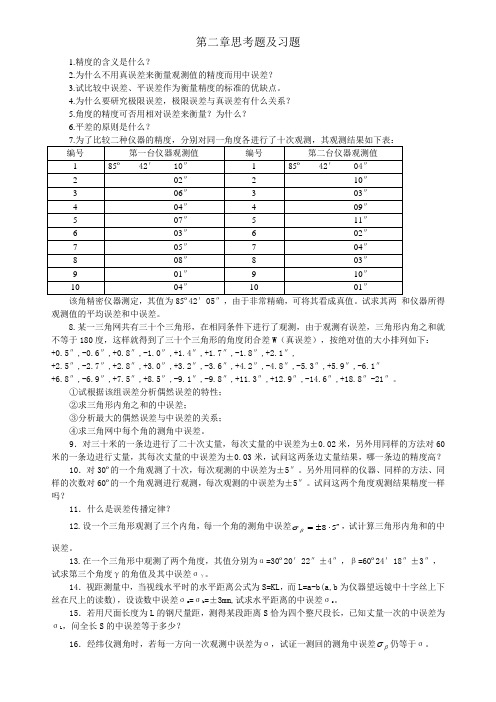
第二章思考题及习题1.精度的含义是什么？2.为什么不用真误差来衡量观测值的精度而用中误差？3.试比较中误差、平误差作为衡量精度的标准的优缺点。

4.为什么要研究极限误差，极限误差与真误差有什么关系？5.角度的精度可否用相对误差来衡量？为什么？6.平差的原则是什么？观测值的平均误差和中误差。

8.某一三角网共有三十个三角形，在相同条件下进行了观测，由于观测有误差，三角形内角之和就不等于180度，这样就得到了三十个三角形的角度闭合差W（真误差），按绝对值的大小排列如下：+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。

①试根据该组误差分析偶然误差的特性；②求三角形内角之和的中误差；③分析最大的偶然误差与中误差的关系；④求三角网中每个角的测角中误差。

9．对三十米的一条边进行了二十次丈量，每次丈量的中误差为±0.02米，另外用同样的方法对60米的一条边进行丈量，其每次丈量的中误差为±0.03米，试问这两条边丈量结果，哪一条边的精度高？10．对30º的一个角观测了十次，每次观测的中误差为±5″。

另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测，每次观测的中误差为±5″。

试问这两个角度观测结果精度一样吗？11．什么是误差传播定律？12.设一个三角形观测了三个内角，每一个角的测角中误差58''⋅±=βσ，试计算三角形内角和的中误差。

13.在一个三角形中观测了两个角度，其值分别为α=30º20′22″±4″，β=60º24′18″±3″，试求第三个角度γ的角值及其中误差σγ。

平差习题库

一、填空题：1、观测条件由观测仪器、____________和_____________三部分构成。

2、观测误差按其性质的不同可分为系统误差和偶然误差，其中____________误差在观测或计算过程中可以采用一定的措施消除或削弱，而___________误差在观测结果中必然存在。

3、测量平差的首要任务是经过数据处理，确定观测值的________________，而__________________________________________也是其必不可少的任务。

4、偶然误差的统计规律性是指：界限性、_______性、_______性和_______性。

5、在某相片上量得一距离长为200㎝，其相对中误差为1/3000,则该距离的绝对中误差为_____________________㎝。

6、测量平差是在______________的基础上利用_______________原理进行的。

7、单位权中误差mo、权Pi和中误差mi之间的关系为_______________________。

8、有一四边形导线环，同精度观测其各内角，共观测5组结果，计算出5个闭合差为﹣8″、9″、7″、﹣5″、-7″，则每组观测值之和中误差为____________，每个导线角观测值中误差___________。

（保留一位小数）9、设某角度观测值的协因数为3，则其观测值的权为_________。

10、观测成果的质量高低__________（能、否）反映观测条件的好坏。

11、理论上我们取3倍中误差为极限误差；而等级控制测量因为观测的精度要求比较高，往往规定______倍中误差为极限误差12、衡量精度常用的几种指标有中误差、___________误差和__________误差。

13、精度是指误差分布的________________程度。

14、由三角形闭合差ω计算测角中误差mβ的公式为______________________。

平差理论及平差基习题集

平差理论及平差基习题集1、在间接平差中，参数X 与平差值L 是否相关？试证明。

答：-111^^2^^^1()(()0T B T T T T T N B PlV B BNbb B Pl L BNbb B E lL L v x xQ x L Q x v Nbb B PQu BNbb P E σ-1-------===-=-=+=+∴==-=σ 2、已知独立观测值L 1、L 2的方差M 1和M 2，求函数211212Y L L L =+的方差。

答：211212112221211212()()Y Y Y L L L L L dL L dL M L L M L M σ=+=++=++3、在相同观测条件下观测A 、B 两个角度，设∠A 观测4测回的权为1，则对∠B 观测9个回合的权是多少？答：2021==114A P σσ20σ221941149LB P σ=== 4、已知观测值向量L21的协方差阵为DLL=3112⎡⎤⎢⎥⎣⎦,又知协因数Q12=1-5，试求观测值。

答：111222200211221202011111220122-1===-13=-1-1=529315513125532LL L L L QL L QL L D Q QL L QL L QL L QL l DL PLL QLL P P σσσσσ---⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦=⎡⎤⎢⎥⎛⎫⎡⎤====⎢⎥ ⎪⎢⎥-⎣⎦⎢⎥⎝⎭⎢⎥⎣⎦==5 、已求得控制网中P 点误差椭圆参数υE=157°30′、E=1.57dm 和F=1.02dm,已知PB 边坐标方位角αPB=217°30′，SPB=5KM,B 为已知点，求方位角中误差^PA σα和边长相对误差^PAPA S S σ。

6、设某平差问题是按条件平差方法进行的，其法方程为：1210-260-246K K -⎡⎤⎡⎤⎡⎤-=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,求联系数12K K ;求单位权方差20σ。

平差理论及平差基习题集

平差理论及平差基习题集1、在间接平差中，参数X 与平差值L 是否相关？试证明。

6、设某平差问题是按条件平差方法进行的，其法方程为：1210-260-246K K -⎡⎤⎡⎤⎡⎤-=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,求联系数12K K ;求单位权方差20σ。

（整理）测量平差习题集

第二部分自测题第一章自测题一、判断题（每题2分，共20分）1、通过平差可以消除误差，从而消除观测值之间的矛盾。

（）2、观测值i L 与其偶然真误差i D 必定等精度。

（）3、测量条件相同，观测值的精度相同，它们的中误差、真误差也相同。

（）4、或然误差为最或然值与观测值之差。

（）5、若X 、Y 向量的维数相同，则YX XY Q Q =。

（）6、最小二乘原理要求观测值必须服从正态分布。

（）7、若真误差向量的数学期望为0，即0=D )(E ，则表示观测值中仅含偶然误差。

（） 8、单位权中误差变化，但权比及中误差均不变。

（）9、权或权倒数可以有单位。

（）10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。

（）二、填空题（每空0.5分，共20分）1、测量平差就是在、测量平差就是在基础上，依据基础上，依据原则，对观测值进行合理的调整，即分别给以适当的别给以适当的，使矛盾消除，从而得到一组最可靠的结果，并进行，使矛盾消除，从而得到一组最可靠的结果，并进行。

2、测量条件包括、测量条件包括、、和，由于测量条件的不可能绝对理想，使得一切测量结果必然含有理想，使得一切测量结果必然含有。

3、测量误差定义为、测量误差定义为，按其性质可分为，按其性质可分为、和。

经典测量平差主要研究的是平差主要研究的是误差。

误差。

4、偶然误差服从、偶然误差服从分布，它的概率特性为分布，它的概率特性为、和。

仅含偶然误差的观测值线性函数服从然误差的观测值线性函数服从分布。

分布。

5、最优估计量应具有的性质为、最优估计量应具有的性质为、和。

若模型为线性模型，则所得最优估计量称为得最优估计量称为，最优估计量主要针对观测值中仅含最优估计量主要针对观测值中仅含误差而言。

要证明某估计量为最优估计量，只需证明其满足某估计量为最优估计量，只需证明其满足性和性和性即可。

平差习题

1 3
，试
写出观测值L 写出观测值 1，L2，L3的中误差及其协方差 σ L L 、σ 和 σ L L 。 LL 2 3 17、协方差的定义式是什么？说明它是怎样描述两个观测值之间的、协方差的定义式是什么？相关关系的？相关关系的？
18、相关观测值向量的协方差阵 X 是怎样定义的？试说明D XX 中各、是怎样定义的？
L1、、
38、设对某量进行三次同精度观测，得独立观测值、设对某量进行三次同精度观测，
L2 、 L3
，
1 L1 V = 1 x − L2 ， 1 L 3
L1 1 x = (1 1 1) L2 由此求得平差值和改正数向量为：，由此求得平差值和改正数向量为： 3 L 3
、
、
14、精度、准确度和精确度分别是怎样定义的？，它们的作用分别、精度、准确度和精确度分别是怎样定义的？，它们的作用分别？，是什么？当观测结果中不存在系统误差时，精确度就是精度吗？是什么？当观测结果中不存在系统误差时，精确度就是精度吗？ 15、设有观测向量X = [ L1 、
21
L2 ]
T
24、、
设函数 Z = F1 X + F2Y ，已知 X 和Y 的协方差阵
D XX , DYY ， X 关于Y 的互协方差阵 D XY 。求 Z
的方差阵 DZZ 和 Z 关于 X 和 Y 的互协方差阵
DZX , DZY 。
25、设有观测向量 L ，其协方差阵为 25、
4 = 3 2
33、、
x
角为
两角之和， L1、 L 2 两角之和， L1 = 32 o18′14′′
，是由16次观测结果平均而得，每次观测中误差为 ± 8′′ ，次观测结果平均而得，是由次观测结果平均而得

测量平差习题集答案

测量平差习题集答案测量平差习题集答案在测量工作中，平差是一项非常重要的环节。

它通过对测量数据进行处理和分析，消除误差，得到更加准确的测量结果。

为了帮助大家更好地理解和掌握平差的方法和技巧，下面将为大家提供一些测量平差习题集的答案。

1. 题目：某测量队在进行水平控制网的测量时，测得A、B两点的水平角为α1=90°30'20"，α2=269°29'40"，A、B两点的距离为1000米。

已知A点的坐标为(1000, 1000)，求B点的坐标。

解答：根据水平角的定义，可以得到以下关系式：α1 = α2 + 180°即90°30'20" = 269°29'40" + 180°化简得90°30'20" = 449°29'40"由于角度超过360°，需要将其转化为小于360°的形式，可以通过减去360°来实现，即：90°30'20" - 360° = 89°29'40"所以，B点的水平角为89°29'40"。

接下来，根据已知的A点坐标和AB距离，可以利用正弦定理来求解B点的坐标。

设B点的坐标为(x, y)，则有：(x - 1000)^2 + (y - 1000)^2 = 1000^2根据正弦定理，可以得到以下关系式：sin(89°29'40") = (x - 1000) / 1000化简得：(x - 1000) = 1000 * sin(89°29'40")解得：x ≈ 1999.999同理，可得：y ≈ 1000.000所以，B点的坐标为(1999.999, 1000.000)。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2．某单位购买了一台新水准仪，经过检测其精度知道，用该仪器单程测量1km 的高差中误 1. 间接平差公式汇编，设观测值的协因数阵为LL Q ，求未知参数平差值的协因数阵。

3．差是5mm 。

该单位接到一个工程任务，其中之一是需要在指定位置建立一个水准点，要求该水准点的高程中误差不大于10mm 。

经过勘查，距该水准点附近有两个高级已知水准点，一个相距约10km ，另外一个相距约20km ，现在两已知水准点之间经过新建的水准点布设一条附合路线，问用新购的水准仪进行单程测量是否满足精度要求。

（使用间接平差解答）。

3．最简单形式的单导线严密平差问题：等精度观测三个角，测角中误差"5=βσ，观测了两条边，cm cm S S 0.2,5.221==σσ，使用间接平差列观测方程并线性化。

4. 在直角多边形中（如图），测得三边之长为21L L 、及3L ，试列出该图的误差方程式。

5．在三角形ABC中，测得不等精度观测值如下：，1,3.11205111="'︒=P β2,9.21088822="'︒=P β，2,4.28314033="'︒=P β，若选取直接观测值的平差值为未知参数，试按照间接平差计算各角的平差值。

6．如图所示的直角三角形ABC 中，已知AB=100.00m （无误差），测得边长AC 和角度A ，得观测值为ml 470.1151=，,5559292"'︒=l 其中误差分别为,51mm l ±=σ,42"±=l σ试按间接平差法求三角形ABC中的平差值。

7. 图4.3中,C B A 、、是已知点, 21P P 、为待定点,网中观测了12个角度和6条边长。

已知测角中误差为5.1''±，边长测量中误差为0.2±cm ，起算数据及观测值分别列表于表4.1和表4.2。

表4.1点号坐标 (m)坐标方位角边长 (m) x y A BC4899.846 8781.945 4548.795130.812 1099.443 7572.62214 00 35.77 123 10 57.974001.117 7734.443表4.2 编号观测角编号观测角编号观测边（m ） 1 2 3 4 56 84 07 38.2 37 46 34.9 58 05 44.1 33 03 03.2 126 01 55.720 55 02.3 7 8 9 10 1112 74 18 16.8 77 27 59.1 28 13 43.2 55 21 09.9 72 22 25.852 16 20.5 13 14 15 16 1718 2463.94 3414.71 5216.23 6042.94 5085.085014.99 8. 是否可以将误差方程式看作附有未知数的条件式？试按附有未知数的条件平差导出普通间接平差的基础方程。

9. 在附有未知数的条件平差当中，试证明：（1）未知数向量X 与改正数向量V 是互不相关的；（2）平差值函数0ˆf X f L f TX T ++=φ与改正数向量V 是互不相关的。

图4.318 17 1615 14 13 12 11 10 9 8 7 6 5 43 2 1 A B C P P10. 试证明：在附有条件的间接平差法中，（1）改正数向量V 与平差值向量Lˆ是互不相关的；（2）联系数向量K 与未知数的函数0f X f T +=φ也是互不相关的。

11. 设有误差方程i i L x v -=ˆ，已知观测值i L （i=1，2，…，n ），精度相同，且权1=i P ，按间接平差法求得参数x 的估值为∑=-==ni iTT n L l B B B x11)()(ˆ试证：未知参数估值xˆ具有无偏性； 12. 设未知数321,,x x x 间互相误差独立，试求未知数函数332211x f x f x f F ++=的权倒数F p /1。

测量平差试题一一、正误判断。

正确“T ”，错误“F ”。

（20 分） 1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．观测值与最佳估值之差为真误差（）。

4．系统误差可用平差的方法进行减弱或消除（）。

5．权一定与中误差的平方成反比（）。

6．间接平差与条件平差一定可以相互转换（）。

7．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

8．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

9．定权时0σ可任意给定，它仅起比例常数的作用（）。

10．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

二、用“相等”或“相同”或“不等”填空（8 分）。

已知两段距离的长度及其中误差为300.158m ±3.5cm; 600.686m ±3.5cm 。

则： 1．这两段距离的中误差（）。

2．这两段距离的误差的最大限差（）。

3．它们的精度（）。

4．它们的相对精度（）。

三、选择填空。

只选择一个正确答案（25 分）。

1．取一长为d 的直线之丈量结果的权为 1，则长为D 的直线之丈量结果的权D P =（）。

a) D d b) d D c) 22D d d) 22dD 2.有一角度测 20 测回，得中误差±0.42 秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（）。

a) 25 b) 20 c) 45 d) 5 3.某平面控制网中一点P ，其协因数阵为：⎢⎣⎡⎥⎦⎤=YY YX XY XX XX Q Q Q Q Q =⎢⎣⎡⎥⎦⎤--5.025.025.05.0 单位权方差20σ =±2.0。

则P 点误差椭圆的方位角 T=（）。

a) 90 b) 135 c) 120 d) 454.设L 的权为1，则乘积4L 的权P=（）。

a) 1/4 b) 4 c) 1/16 d) 16 5.设⎢⎣⎡⎥⎦⎤21y y ＝⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤--213112x x ；⎢⎣⎡⎥⎦⎤=4113XX D ,设F = y2+ x1，则2F m =（）。

a) 9 b) 16 c) 144 d) 36四、某平差问题是用间接平差法进行的，共有 10 个独立观测值，两个未知数，列出 10 个误差方程后得法方程式如下（20分）：⎢⎢⎣⎡⎥⎥⎦⎤⎢⎣⎡⎥⎦⎤--∧∧2182210x x ＝⎢⎣⎡⎥⎦⎤--146 且知[pll]=66.0。

求：1．未知数的解 2．单位权中误差0m 3．设F = ∧∧+2134x x ；求Fp 1五、试用文字符号列出下列三角网的条件方程式。

六、在某测边网中，设待定点P 1的坐标为未知参数，即[]11ˆTX X Y =，平差后得到ˆX的协因数阵为ˆˆ0.250.150.150.75XX Q ⎡⎤=⎢⎥⎣⎦，且单位权方差220ˆ 3.0cm σ=，（1）计算P 1点纵、横坐标中误差和点位中误差；（2）计算P 1点误差椭圆三要素E E F ϕ、、；（3）计算P 1点在方位角为90方向上的位差。

(17分)试题一答案一、FFFFT TTTTF二、相等相等相同不等三、aabcd四、0=-∧BPl x PB B T⎢⎣⎡⎥⎦⎤--=⎢⎣⎡⎥⎦⎤--⎢⎣⎡⎥⎦⎤--=-∧21146822101x2、tn PVV T -±=0σ⎢⎣⎡⎥⎦⎤--⎢⎣⎡⎥⎦⎤---=-=∧-2114666)(1x PB B pl l PV V TtT=32 其中 n =10,t = 28320±=σ2±= ][⎢⎢⎣⎡⎥⎦⎤=222134σσFFQ ⎢⎣⎡⎥⎦⎤34021σσσ==Fp 1=FF Q =25五.六. （1）3ˆˆˆ1.532x y p cm cm cm σσσ===，，（2） 1.540.79E E cm F cm ϕ== =74.5或254.5，，（3）90ˆ 1.5cm ψσ==测量平差试题一一、正误判断。