分岔图做法[1]
绘制Duffing振子的分叉图的程序

绘制Duffing振子的分叉图的程序这些程序思想有些可能不正确,有问题,自己改进,我不再负责对这些程序解释。
因为我都不知道道理在哪里。
但是期望您能在程序的提示下,进一步的做改进或者改正,以期获得更为精确的结果。
别照搬和迷恋别人的程序!% % %%%% 绘制Duffing振子的庞加莱截面图的程序% % buchang:已知激励下步长数值的大小, % % tend程序仿真达到150个激励周期的总时间,% clear;clc% global m c k1 k3 F0 omega%%m=1;c=0.1;k1=0;k3=1;omega=1;F0=12 % x0=[3;4];%tstart=0;Tbushu=600;buchang=(2*pi/o mega)/Tbushu;tend=(2*pi/omega)*150; % tspan=[tstart:buchang:tend];% [t,y]=ode45('dafin3',tspan,x0);%count=find(t>(2*pi/omega*40));% 去掉前40个周期的激励时间以消除瞬态响应的影响% Y=y(count,:);%TData=Y(1:Tbushu,1)-Y((Tbushu+1):Tbu shu*2,1);% [maxvalue,indices]=max(abs(TData)) %pointnumber=round((tend-2*pi/omega* 40)/buchang/Tbushu)-1;% dis=zeros(pointnumber,1);% velo=zeros(pointnumber,1);% for i=1:pointnumber%dis(i,1)=Y(Tbushu*(i-1)+indices,1);%velo(i,1)=Y(Tbushu*(i-1)+indices,2);% end% figure,plot(dis,velo,'b.','markersize',5);% %%%% 绘制Duffing振子的分叉图的程序% clear;clc% global m c k1 k3 F0 omega;% m=1;k1=0;k3=1;omega=1;F0=12;% range=[0.01:0.01:1];% YY=[];k=0;% for c=range% k=k+1;% y0=[3,4];% tspan=[0:0.01:200];% [t,Y]=ode45('dafin3',tspan,y0);% count=find(t>100);% Y=Y(count,:);% % 画x的分岔图。
分岔与混沌

化会引起特征值的变化,当控制参数达到分
岔参数值时,系统稳定性发生质的变化,它
可以表现为 ( ) 在复平面的运动。由此也可以
定义三种分岔类型:
2022/1/10
机械系统与振动国家重点实验室
9
叉型分岔
霍普分岔
特征值 为
实数,沿复
平面的实轴由
负变正穿过虚
轴。
平衡点
x 0 和 x= ,
x 0,
而对应特征值则为
0
0
x2
对于图3,当 c时,平衡态的一个分支是稳定的;然而当 c时,这
一支就变得不稳定了;一旦当 c 有新的平衡分支解 x 又变成稳
定的了,这种情况被称为超临界分岔。反过来,若新的平衡分支解x
2022/1/10
机械系统与振动国家重点实验室
22
庞加莱-伯克霍夫(PB)规范形方法
考虑微分方程
x=f(x),x∈Rn
(1)
设f(x)足够光滑,且f(0)=0。
现在研究对于某个给定正整数r≥2,通过坐标的多项式变换,
使得在f的泰勒展开式中直到r次的项都有比较简单的形式。
庞加莱伯克霍夫范式定理 设f(x)是Cr向量场(r≥2),f
23
庞加莱-伯克霍夫(PB)规范形方法
需要注意:
1.对于给定的r来说,r阶PB范式的取法一般不是唯一的。
2.在平衡点附近,截断规范形系统与原来的系统的拓扑结
构往往有密切的关系,但并不一定相同。一般来说,对于
给定的r,r阶PB范式到底能在多大程度上反映原系统的定
性性态仍然是一个未完全解决的问题。
3.尽管如此,在大量研究中发现,阶数不太高的PB范式通
分岔图做法[1]
![分岔图做法[1]](https://img.taocdn.com/s3/m/ff8b4155be23482fb4da4c67.png)
>>混沌研究总结篇------一、分岔图(1.Chen系统)先打个提纲,这几天把自己混沌相关知识研究学习内容总结一下。
首先简绍几个基本概念:一、自治系统一个n阶自治的连续动态系统可以表示为可以理解为对于自治的连续系统,上相量场f是不依赖于时间t的。
二、非自治系统一个n阶非自治的连续动态系统可以表示为可以理解为对于非自治的连续系统,向量场f不仅依赖于状态变量x,而且依赖于时间t,如Duffing振子。
三、庞加莱映射庞加莱映射是一个传统的用来离散化连续系统的方法。
庞加莱映射可以用(n-1)阶的离散映射来取代n阶的连续系统。
庞加莱映射的用处正在于减小系统的阶数,并且在连续系统和离散系统之间建立了一座桥梁。
对于n阶自治系统,其对应的解对就着轨迹。
当选择作为一个(n-1)维的超平面,这样轨迹将穿越超平面。
难点主要是超平面的选取,使其对应的解穿越超平面,就可以得到一个领域内的庞加莱映射。
对于n阶非自治系统,若其外加强迫力的最小周期是T,j最终的庞加莱映射可以定义为相应的轨道P(xk)是对某个轨迹每隔T时刻采样一次获得,这种操作和每隔T时刻的频闪观测仪的行为很相似。
所以要想得到一个系统的庞加莱映射,这段话一定要好好理解,当真真知道这中间说的含义,庞加莱映射这么画其实也已经知道国。
四、分岔图分岔图的横坐标是一个变化的参数,纵坐标是你要求的某一个量的随着各参数的变化情况,而poincare则是我们选取横坐标上的某参数的某一个具体值时截面图,只不过poincare截面的选取其实可以是任意的。
下面主要研究的混沌系统有:Logistic、Henon、Lorenz、Duffing、Rossler、Chen、混沌电机模型等系统1.Chen系统先说Chen系统,因为和课题有一定的关系,而且自己以后起家也得从Chen 系统入手。
系统方程如下:dx/dt=a*(y-x)dy/dt=(c-a)*x+c*y-x*zdz/dt=x*y-b*z就是对此方程中不同参数a、b、c下对系统画分岔图,研究混沌系统(1)给定a、c,画b关于系统的分岔图结果如下图所示CODE:function fenchatuchenclc;clearXA=35;XC=28;Z=[];for XB=linspace(2,5.5,100);options = odeset('RelTol',1e-6,'AbsTol',[1e-4 1e-4 1e-5]);[T,X]=ode45('chen',[0,50],[-5 0 5],options,XA,XB,XC);n=length(X);for k=round(n/2):nif abs(X(k,1))<1Z=[Z,XB+abs(X(k,2))*i];endendendfigureplot(Z,'.','markersize',1)title('chen映射分岔图')xlabel('b'),ylabel('|x| where x=0')这组代码不完全是自己的,现在见解其中一些方法在进行自己系统的绘制,这个程序的具体原理我会在后面给出来的。
第七节 分岔管
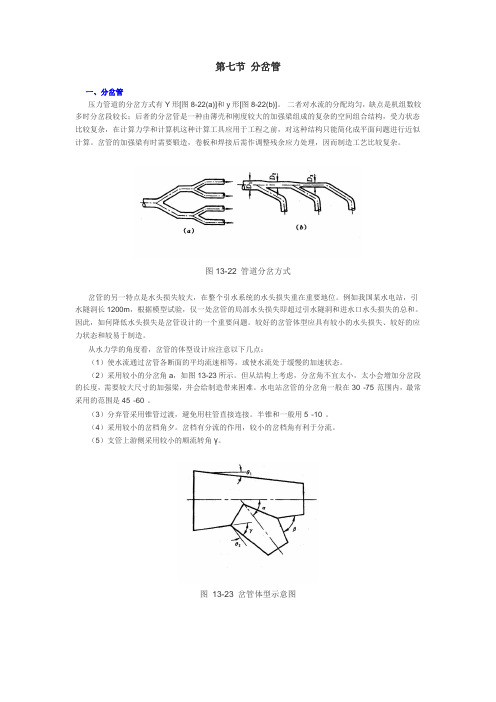
第七节分岔管一、分岔管压力管道的分岔方式有Y形[图8-22(a)]和y形[图8-22(b)]。
二者对水流的分配均匀,缺点是机组数较多时分岔段较长;后者的分岔管是一种由薄壳和刚度较大的加强梁组成的复杂的空间组合结构,受力状态比较复杂,在计算力学和计算机这种计算工具应用于工程之前,对这种结构只能简化成平面问题进行近似计算。
岔管的加强梁有时需要锻造,卷板和焊接后需作调整残余应力处理,因而制造工艺比较复杂。
图13-22 管道分岔方式岔管的另一特点是水头损失较大,在整个引水系统的水头损失重在重要地位。
例如我国某水电站,引水隧洞长1200m,根据模型试验,仅一处岔管的局部水头损失即超过引水隧洞和进水口水头损失的总和。
因此,如何降低水头损失是岔管设计的一个重要问题。
较好的岔管体型应具有较小的水头损失、较好的应力状态和较易于制造。
从水力学的角度看,岔管的体型设计应注意以下几点:(1)使水流通过岔管各断面的平均流速相等,或使水流处于缓慢的加速状态。
(2)采用较小的分岔角a,如图13-23所示。
但从结构上考虑,分岔角不宜太小,太小会增加分岔段的长度,需要较大尺寸的加强梁,并会给制造带来困难。
水电站岔管的分岔角一般在30°-75°范围内,最常采用的范围是45°-60°。
(3)分弃管采用锥管过渡,避免用柱管直接连接。
半锥和一般用5°-10°。
(4)采用较小的岔档角夕。
岔档有分流的作用,较小的岔档角有利于分流。
(5)支管上游侧采用较小的顺流转角γ。
图13-23 岔管体型示意图以上各点有时难于同时满足,例如,增加支管锥角有助于减小γ,但又不可避免地会加大β,但前者对水流的影响较大。
岔管的水力要求和结构要求也存在矛盾,例如,较小的分岔角对水流有利,但对结构不利,因为分岔角越小,管壁互相切割的破口越大,加强梁的尺寸也就越大,而且过小的夹角会使岔档部位的焊接困难,又例如,支管用锥管过渡对水流有明显的好处,但不可避免地会使主支间的破口加大;等等。
3.1-分岔

4.霍夫型分岔
分岔分析
1/(2t C) 0
/(1 Ce2t ) 0
参数μ从负变到正,从焦点
产生出极限环,这种分岔称
霍夫分岔。分岔点位于μ=0。
4.霍夫型分岔
极限环
Hopf 分岔有超临界和亚临界的区别
二 平方映射与倍周期分岔
1. 平方映射 2. 平方映射的不动点及其稳定性 3. 平方映射的周期解
第 n 代数量: Nn 第 n+1 代数量: Nn1
A 如不考虑生存环境对种群生存的影响,第 n 代与第 n+1代有
如下关系:
Nn1 RN n
当 R >1,种群数量将线性地无限制增长。
1.平方映射
平方映射导出—生态平衡方程
B 种群受环境制约,数量有最大限额 N0 ,种群繁殖空间 N 0 N n ,第 n 代与第 n+1代关系
数学模型
dx
dt dy
y x[ (x 2 x y[ (x 2
y 2 )] y 2 )]
dt
引入极坐标
x2 y2
x cos
y
sin
求导
d
dt
(
2
)
d 1
dt
代入原方程
令正弦余弦系数 相等
dx
dt dy
d
dt
d
cos cos
sin cos
dt dt
Nn1 KNn (N0 Nn )
N n1
N n (1
Nn N0
)
K N0
xn1 xn (1 xn )
xn Nn / N0
1.平方映射
平方映射计算
方程展开 xn1 xn (1 xn ) xn xn2
非线性电路系统的动力学行为及其分岔分析

非线性电路系统的动力学行为及其分岔分析非线性电路系统的动力学行为及其分岔分析摘要:非线性电路系统在动力学行为方面具有丰富的特性,它们可能表现出稳定、震荡、混沌等不同的动态行为。
本文将介绍非线性电路系统的动力学行为,并采用分岔分析方法对其进行研究。
一、引言在电子工程领域,非线性电路系统是一类重要的研究对象。
相比于线性电路系统,非线性电路系统的特点是输入与输出之间的关系不是简单的比例关系,而是更为复杂的非线性关系。
由于非线性关系的存在,非线性电路系统在动力学行为方面具有较为丰富的特性。
因此,了解非线性电路系统的动力学行为对于电子工程领域的研究和应用具有重要意义。
二、非线性电路系统的动力学行为非线性电路系统的动力学行为往往表现为稳定、震荡和混沌等不同的行为模式。
1. 稳定行为当非线性电路系统中的稳定解存在且稳定时,系统的输出将收敛到该稳定解。
这种行为模式常见于放大器、滤波器等电路系统中。
稳定解的存在为非线性电路系统的正常工作奠定了基础。
2. 震荡行为在一些特定的条件下,非线性电路系统可能表现出震荡行为。
震荡行为是指系统的输出在一定的时间范围内呈现周期性变化的特征。
震荡行为常见于振荡器电路系统中,如LC振荡电路、RC相移振荡电路等。
震荡行为的存在为电子工程中的时钟电路、无线电收发系统等提供了基础。
3. 混沌行为非线性电路系统在某些特定的条件下还可能表现出混沌行为。
混沌行为是指系统的输出呈现出无规律、无确定性的变化特征。
混沌行为往往需要较复杂的非线性元件和电路结构才能产生,具有一定的应用价值。
例如,混沌发生器可用于保密通信、随机数生成等领域。
三、非线性电路系统的分岔分析分岔分析是一种研究非线性系统动力学行为的重要工具。
它通过改变系统中的某个参数,观察系统响应的变化,从而揭示系统的稳定性和动态特性。
1. 变量选择在分岔分析中,需要选择适当的变量来描述系统的动力学行为。
常用的变量选择包括电压、电流、相位差等。
[转载]分岔图绘制不同方法的总结、比较(转)
![[转载]分岔图绘制不同方法的总结、比较(转)](https://img.taocdn.com/s3/m/c3a41200a31614791711cc7931b765ce05087afd.png)
[转载]分岔图绘制不同⽅法的总结、⽐较(转)原⽂地址:分岔图绘制不同⽅法的总结、⽐较(转)作者:海武⼠分岔图绘制不同⽅法的总结、⽐较2008-03-14 08:13经过近期的研究发现,⽬前对于系统单参数分岔图的计算共有以下的⼏种⽅法:1)最⼤值法即对系统微分⽅程(组)进⾏求解,对求解的结果⽤getmax函数进⾏取点,并绘图。
2)Poincare截⾯法对系统参数的每⼀次取值,绘制其Poincare截⾯,进⽽得到其分岔图。
这种⽅法需要注意的是,⾃治系统的Poincare截⾯是选取⼀超平⾯,平⾯上点的分布即构成⼀Poincare截⾯,⾮⾃治系统的Po incare截⾯则是根据系统激励的频率进⾏取点并绘图。
本帖将以Lorenz系统为例,对这两种⽅法进⾏⽐较⾸先对第⼆种⽅法进⾏阐述。
编程如下(matlab)Lorenz系统:function dy = Lorenz(t,y)% Lorenz系统% 系统微分⽅程:% dx/dt = -a(x-y)% dy/dt = x(r-z)-y% dz/dt = xy-bz% a=y(4)% r=y(5)% b=y(6)dy=zeros(6,1);dy(1)=-y(4)*(y(1)-y(2));dy(2)=y(1)*(y(5)-y(3))-y(2);dy(3)=y(1)*y(2)-y(6)*y(3);dy(4)=0;dy(5)=0;dy(6)=0;随r的分岔图求解程序:——按照x=y平⾯取截⾯function Lorenz_bifur_rZ=[];for r=linspace(1,500,1000);% 舍弃前⾯迭带的结果,⽤后⾯的结果画图[T,Y]=ode45('Lorenz',[0,1],[1;1;1;16;r;4]);[T,Y]=ode45('Lorenz',[0,50],Y(length(Y),:));Y(:,1)=Y(:,2)-Y(:,1);% 对计算结果进⾏判断,如果点满⾜x=y,则取点for k=2:length(Y)f=k-1;if Y(k,1)<0if Y(f,1)>0y=Y(k,2)-Y(k,1)*(Y(f,2)-Y(k,2))/(Y(f,1)-Y(k,1)); Z=[Z r+abs(y)*i];endelseif Y(f,1)<0y=Y(k,2)-Y(k,1)*(Y(f,2)-Y(k,2))/(Y(f,1)-Y(k,1)); Z=[Z r+abs(y)*i];endendendendplot(Z,'.','markersize',1)title('Lorenz映射分岔图')xlabel('r'),ylabel('|y| where x=y')结果如图1所⽰。
基于Matlab实现离散系统分岔图的绘制

基于Matlab实现离散系统分岔图的绘制⽬录1.⼀维离散分岔图2.⼆维离散分岔图3.封⾯图绘制1.⼀维离散分岔图⼀维那⾮常简单哈,就循环着画呗,以下举两个简单的例⼦:% x(n+1)=1-r*x(n)^2% (r∈(0,2),x∈[-1,1])的分⽀混沌图。
hold onf=@(x,r)1-r.*x.^2;r=0:.01:2;x=0; % x初值for n=1:1000x=f(x,r);if n>100 % 稳定后开始绘图plot(r,x,'k.','MarkerSize',1);drawnowendend% Logistic系统% x(n+1)=r*x(n)-r*x(n)^2% (r∈(2.6,4),x∈(0,1])的分⽀混沌图。
hold onf=@(x,r)r.*x-r.*x.^2;r=2.6:.01:4;x=0.6; % x初值for n=1:1000x=f(x,r);if n>100 % 稳定后开始绘图plot(r,x,'k.','MarkerSize',1);drawnowendend横坐标代表参数的数值,纵坐标表⽰该参数数值下序列可能的取值,n>100再开始画图是为了让序列通过迭代稳定下来,事实上我么可以不设置n>100,同时将颜⾊设置为随着n变化的渐变⾊,可以发现⼏乎看不出渐变来,该序列稳定的很快(以下是绘图部分代码的微调):c1=[0 0.4470 0.7410];c2=[0.6350 0.0780 0.1840];N=1000;for n=1:Nx=f(x,r);plot(r,x,'.','Color',(n.*c1+(N-n).*c2)./N,'MarkerSize',2);drawnowend当然我们可以设置n为奇数和偶数时绘制不同颜⾊,下图所⽰,对于该系统⽽⾔,其序列的数值是反复横跳的(以下是绘图部分代码的微调):当然可以设置更多颜⾊:for n=1:1000x=f(x,r);switch mod(n,4)case 3,plot(r,x,'.','Color',[0.4660 0.6740 0.1880],'MarkerSize',2);case 2,plot(r,x,'.','Color',[0.8500 0.3250 0.0980],'MarkerSize',2);case 1,plot(r,x,'.','Color',[0 0.4470 0.7410],'MarkerSize',2);case 0,plot(r,x,'.','Color',[0.6350 0.0780 0.1840],'MarkerSize',2);enddrawnowend2.⼆维离散分岔图绘制Henon系统的分岔图:定住b值不变,改变a值,观察y序列,不同b值时绘制效果不同:% x(n+1)=1+y(n)-a*x(n)^2% y(n+1)=b*x(n)% Henon系统hold onfx=@(x,y,a)1+y-a.*x.^2;fy=@(x,b)b.*x;a=0:.002:1.4;b=0.2;x=0;y=0;for n=1:800lx=x;ly=y;x=fx(lx,ly,a);y=fy(lx,b);if n>100 % 稳定后开始绘图plot(a,y,'k.','MarkerSize',1);drawnowendendb=0.2时绘制效果b=0.3时绘制效果3.封⾯图绘制经典体现理科⽣⼯科⽣艺术情怀环节,我们怎么能够将分岔图的美忽视?感觉⼤家很多也是因为看封⾯图点进来的,虽然不短,但还是把代码放⼀下叭,原理很简单,构造⼀个矩阵统计各个位置点数量,然后依据点数量映射到颜⾊:图⼀% x(n+1)=1+y(n)-a*x(n)^2% y(n+1)=b*x(n)% Henon系统fx=@(x,y,a)1+y-a.*x.^2;fy=@(x,b)b.*x;a=0:.002:1.4;b=0.3;x=0;y=0;% 填充矩阵pntMat=zeros(451,701);for n=1:12000lx=x;ly=y;x=fx(lx,ly,a);y=fy(lx,b);disp(['进度:[',num2str(n),'/12000]']);ty=round((y+0.4)*500);ta=a*500;index=round((ta).*451+ty);pntMat(index)=pntMat(index)+1;end% 矩阵上下翻转(坐标y轴⽅向与图⽚序数相反)pntMat=flipud(pntMat);% 绘图imagesc(pntMat);caxis([0,50])ax=gca;hold on;ax.XTick=[];ax.YTick=[];% 颜⾊映射map=[0.1294 0.0549 0.1725;0.2196 0.1608 0.2902;0.3882 0.1804 0.4941;0.4392 0.1922 0.4706;0.5333 0.2235 0.4392;0.6471 0.2588 0.3686;0.7137 0.2745 0.3294;0.7725 0.3059 0.2902;0.8510 0.3725 0.2275;0.9137 0.4196 0.1804;0.9608 0.5020 0.2000;0.9765 0.5529 0.2078;0.9804 0.6431 0.2549;0.9843 0.6627 0.2706;0.9765 0.7176 0.3412;0.9765 0.7686 0.4000;0.9765 0.8118 0.4902;0.9725 0.8510 0.5961;0.9882 0.9020 0.6667;1.0000 0.9451 0.8431;1.0000 0.9961 0.9804;1.0000 1.0000 1.0000];Xi=1:size(map,1);Xq=linspace(1,size(map,1),800);map=[interp1(Xi,map(:,1),Xq,'linear')',...interp1(Xi,map(:,2),Xq,'linear')',...interp1(Xi,map(:,3),Xq,'linear')'];colormap(map)图⼆% x(n+1)=1-r*x(n)^2% (r∈(0,2),x∈[-1,1])的分⽀混沌图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
>>混沌研究总结篇------一、分岔图(系统)先打个提纲,这几天把自己混沌相关知识研究学习内容总结一下。
首先简绍几个基本概念:一、自治系统一个n阶自治的连续动态系统可以表示为可以理解为对于自治的连续系统,上相量场f是不依赖于时间t的。
二、非自治系统一个n阶非自治的连续动态系统可以表示为可以理解为对于非自治的连续系统,向量场f不仅依赖于状态变量x,而且依赖于时间t,如Duffing振子。
三、庞加莱映射庞加莱映射是一个传统的用来离散化连续系统的方法。
庞加莱映射可以用(n-1)阶的离散映射来取代n阶的连续系统。
庞加莱映射的用处正在于减小系统的阶数,并且在连续系统和离散系统之间建立了一座桥梁。
对于n阶自治系统,其对应的解对就着轨迹。
当选择作为一个(n-1)维的超平面,这样轨迹将穿越超平面。
难点主要是超平面的选取,使其对应的解穿越超平面,就可以得到一个领域内的庞加莱映射。
对于n阶非自治系统,若其外加强迫力的最小周期是T,j最终的庞加莱映射可以定义为相应的轨道P(xk)是对某个轨迹每隔T时刻采样一次获得,这种操作和每隔T时刻的频闪观测仪的行为很相似。
所以要想得到一个系统的庞加莱映射,这段话一定要好好理解,当真真知道这中间说的含义,庞加莱映射这么画其实也已经知道国。
四、分岔图分岔图的横坐标是一个变化的参数,纵坐标是你要求的某一个量的随着各参数的变化情况,而poincare则是我们选取横坐标上的某参数的某一个具体值时截面图,只不过poincare截面的选取其实可以是任意的。
下面主要研究的混沌系统有:Logistic、Henon、Lorenz、Duffing、Rossler、Chen、混沌电机模型等系统系统先说Chen系统,因为和课题有一定的关系,而且自己以后起家也得从Chen系统入手。
系统方程如下:dx/dt=a*(y-x)dy/dt=(c-a)*x+c*y-x*zdz/dt=x*y-b*z就是对此方程中不同参数a、b、c下对系统画分岔图,研究混沌系统(1)给定a、c,画b关于系统的分岔图结果如下图所示CODE:function fenchatuchenclc;clearXA=35;XC=28;Z=[];for XB=linspace(2,,100);options = odeset('RelTol',1e-6,'AbsTol',[1e-4 1e-4 1e-5]);[T,X]=ode45('chen',[0,50],[-5 0 5],options,XA,XB,XC);n=length(X);for k=round(n/2):nif abs(X(k,1))<1Z=[Z,XB+abs(X(k,2))*i];endendendfigureplot(Z,'.','markersize',1)title('chen映射分岔图')xlabel('b'),ylabel('|x| where x=0')这组代码不完全是自己的,现在见解其中一些方法在进行自己系统的绘制,这个程序的具体原理我会在后面给出来的。
后面将陆续简绍其它混沌系统分岔图、吸引子、时间序列、功率普等的求取。
混沌研究总结篇------一、分岔图(混沌电机系统)今天算是把混沌电机模型跑出一组分岔图,和理论预期基本一样。
2.混沌电机模型系统模型如下:dx/dt = z*y - xdy/dt = -z*x - y+gama*zdz/dt= dita*(y - z)仿真结果如下:通过波形我们可以看出,当gama=左右出现分岔,当gama=7左右时,出现二周期;当gama=左右,系统工作在混沌状态下。
由此,通过调整gama参数,可以得到系统工作在周期或是混沌状态下。
当gama=20时,得到系统的吸引子如下,可以看出,系统工作在混沌状态下。
混沌研究总结篇------一、分岔图(3.其于的一些自治系统)系统系统形式如下:dx/dt = a*(y - x)dy/dt = R*x - y -x*zdz/dt= x*y - b*z仿真结果:系统系统形式如下: dx/dt = -y - zdy/dt = x + a*y dz/dt= b + z*(x - c)仿真结果:系统x(n+1)=1+a*x(n)^2+y(n) y(n+1)=b*x(n)仿真结果:系统x(n+1)=a*(1-x(n))*x(n) 仿真结果:混沌研究总结篇------一、分岔图(4.一些非自治系统)下面简绍一个非自系统分岔图的画法:(不断完善)对于非自治系统的Poincare截面一般选为其周期激振的整周期倍,poincare截面取点就是每个周期里取一个相空间里的点作图采用的方法叫频闪法。
系统系统方程如下:dx/dt=ydy/dt=-x-x^3-det*y-gama*cos(wt)仿真结果:混沌研究总结篇------二、Lyapunov指数(1.连续系统)关于Lyapunov指数指数的计算,网上也有很多总结,比较总结好的一个是出自(百思论坛),这上面总结的很详细,具体用法,应用场合都简绍到了,下面我主要以此为依据,把自己的想法写下。
参考书目:吕金虎《混沌时间序列分析及其应用》、邹国棠《混沌电机驱动及其应用》参考文献:《李雅普诺夫指数谱的研究与仿真》等一、基本概念混沌系统的基本特点就是系统对初始值的极端敏感性,两个相差无几的初值所产生的轨迹,随着时间的推移按指数方式分离,lyapunov指数就是定量的描述这一现象的量。
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。
对于系统是否存在动力学混沌, 可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov 指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。
Lyapunov指数的和表征了椭球体积的增长率或减小率,对Hamilton 系统,Lyapunov指数的和为零; 对耗散系统,Lyapunov指数的和为负。
如果耗散系统的吸引子是一个不动点,那么所有的Lyapunov指数通常是负的。
如果是一个简单的m维流形(m = 1或m = 2分别为一个曲线或一个面) ,那么,前m 个Lyapunov指数是零,其余的Lyapunov指数为负。
不管系统是不是耗散的,只要λ1 > 0就会出现混沌。
微分动力系统L yapunov指数的性质对于一维(单变量) 情形,吸引子只可能是不动点(稳定定态) 。
此时λ是负的。
对于二维情形, 吸引子或者是不动点或者是极限环。
对于不动点,任意方向的δxi , 都要收缩, 故这时两个Lyapunov指数都应该是负的, 即对于不动点, (λ1 ,λ2 ) = ( - , - ) 。
至于极限环,如果取δxi 始终是垂直于环线的方向,它一定要收缩,此时λ < 0;当取δxi沿轨道切线方向,它既不增大也不缩小,可以想像,这时λ = 0。
事实上,所有不终止于定点而又有界的轨道(或吸引子) 都至少有一个Lyapunov指数等于零,它表示沿轨线的切线方向既无扩展又无收缩的趋势。
所以极限环的Lyapunov指数是(λ1 ,λ2 ) = (0, - ) 。
在三维情形下有(λ1 ,λ2 ,λ3 ) = ( - , - , - ) :稳定不动点;(λ1 ,λ2 ,λ3 ) = (0, - , - ) :极限环;(λ1 ,λ2 ,λ3 ) = (0, 0, - ) :二维环面;(λ1 ,λ2 ,λ3 ) = ( +, +, 0) :不稳极限环;(λ1 ,λ2 ,λ3 ) = ( +, 0, 0) :不稳二维环面;(λ1 ,λ2 ,λ3 ) = ( +, 0, - ) :奇怪吸引子。
李雅谱诺夫指数小于零,则意味着相邻点最终要靠拢合并成一点,这对应于稳定的不动点和周期运动;若指数大于零,则意味着相邻点最终要分离,这对应于轨道的局部不稳定,如果轨道还有整体的稳定因素(如整体有界、耗散、存在捕捉区域等),则在此作用下反复折叠并形成混沌吸引子。
指数越大,说明混沌特性越明显,混沌程度越高。
二、lyapunov指数的求取(主要参考网上给出的那篇总结)1. 关于连续系统Lyapunov指数的计算方法连续系统LE的计算方法主要有定义方法、Jacobian方法、QR分解方法、奇异值分解方法,或者通过求解系统的微分方程,得到微分方程解的时间序列,然后利用时间序列(即离散系统)的LE求解方法来计算得到。
最常用的主要以定义方法、Jacobian方法做主要介绍内容。
这两种方法的计算方法在这里不做简绍,很容易查到,下面说下其具体应用场合:一般地,如果已知系统方程(当然系统不能太过复杂)时,则计算Lyapunov 指数采用定义法、Jacobian方法要精确、简单些!Jacobian方法我们可以使用LET工具箱,基本原理就是首先求解出连续系统微分方程的近似解,然后对系统的Jacobian矩阵进行QR分解,计算Jacobian矩阵特征值的乘积,最后计算出LE和分数维。
对于我们觉的连续系统,如Lorenz、Henon、Duffing等的Lyapunov指数都可以用定义法或是Jacobian方法求取。
(1)下面是那篇总结中给出的计算Rossler吸引子的Lyapunov指数结果:(2)关于LET工具箱下载地址:使用手册:这个软件可以计算自己编写的程序,点击Run Let Main program,然后选择setting,输入自己编辑的函数文件(按照软件要求的格式),同时进行各种参数设置即可进行计算。
下面说明一下该工具箱:(参考oct)(1) LET工具箱适用于连续系统,如Logistic、Henon、Lorenz、Duffing、Rossler、Chen,但对时间序列的LE求解不适用(2)在进行LET求解之前,需要注意应将非自治系统写成自治系统的形式,然后参考工具箱给出的Lorenz、Rossler系统的例子,将微分方程定义函数写成标准形式(3)用let求解Lyapunov指数,在设置窗口中设置相关参数即可!具体设置界面如下:点击Run Let Main program后得到如下:选择setting后后得到如下:(1)在ODE Function处填写自己编的函数文件名,m文件格式一定要与给的Demo相同,参考Henon或是Lorenz系统这m文件,很容易写出自己的函数文件。
(2)在Intial Condition处填写系统的初值,如Heno映射的初值[0;0],直接写0 0即可。
