fgk算法编码过程
编码与解码算法原理与实现

编码与解码算法原理与实现一、引言编码和解码是计算机科学中的两个重要概念。
编码是指将信息从一种形式转换为另一种形式,而解码则是将编码后的信息转换回原始形式。
在计算机领域,编码和解码算法被广泛应用于数据传输、存储以及安全等方面。
本文将详细介绍编码与解码算法的原理和实现步骤。
二、编码算法原理与实现步骤编码算法是将信息转换为另一种形式的过程。
常见的编码算法包括Base64、哈夫曼编码等。
下面以Base64编码算法为例,介绍其原理和实现步骤。
1. 原理Base64编码算法是一种用64个字符来表示任意二进制数据的方法。
它将原始信息分割成固定长度的块,并将每个块转换为对应的Base64字符。
转换的过程包括以下步骤:- 将原始信息转换为二进制数据;- 对二进制数据进行分割,每个分割后的块长度为24位,不足24位的在末尾补0;- 对每个24位块进行转换,将其分割为4个6位的块;- 将每个6位块转换为对应的Base64字符;- 将转换后的Base64字符拼接起来,即为编码后的结果。
2. 实现步骤Base64编码算法的实现可以分为以下几个步骤:- 将原始信息转换为二进制数据:首先,将原始信息转换为ASCII码表示的字符;然后,将每个字符转换为对应的二进制数据;- 对二进制数据进行分割,每个分割后的块长度为24位:将二进制数据按照每24位进行分割,并在末尾补0;- 对每个24位块进行转换,将其分割为4个6位的块:将每个24位块拆分为4个6位的块,保存起来备用;- 将每个6位块转换为对应的Base64字符:将每个6位的块转换为对应的Base64字符;- 将转换后的Base64字符拼接起来,即为编码后的结果:将转换后的Base64字符按照顺序拼接起来,即可得到编码后的结果。
三、解码算法原理与实现步骤解码算法是将编码后的信息转换回原始形式的过程。
下面以Base64解码算法为例,介绍其原理和实现步骤。
1. 原理Base64解码算法是将Base64编码后的信息转换回原始形式的方法。
算术编码与解码

算术编码与解码1、编码过程算术编码方法是将被编码的一则消息或符号串(序列)表示成0和1之间的一个间隔(Interval),即对一串符号直接编码成[0,1]区间上的一个浮点小数。
符号序列越长,编码表示它的间隔越小,表示这一间隔所需的位数就越多。
信源中的符号序列仍然要根据某种模式生成概率的大小来减少间隔。
可能出现的符号概率要比不太可能出现的符号减少范围小,因此,只正加较少的比特位。
在传输任何符号串之前,0符号串的完整范围设为[0,1]。
当一个符号被处理时,这一范围就依据分配给这一符号的那一范围变窄。
算术编码的过程,实际上就是依据信源符号的发生概率对码区间分割的过程。
输入:一个字符串输出:一个小数考虑某条信息中可能出现的字符仅有a b c 三种,要压缩保存的信息为bccb。
假设对a b c 三者在信息中的出现概率一无所知(采用自适应模型),暂时认为三者的出现概率相等,也就是都为1/3,将0 - 1 区间按照概率的比例分配给三个字符,即a 从0.0000 到0.3333,b 从0.3333 到0.6667,c 从0.6667 到 1.0000。
用图形表示就是:+-- 1.0000 | Pc = 1/3 | | +-- 0.6667 | Pb = 1/3 | | +-- 0.3333 | Pa = 1/3 | | +-- 0.0000对于第一个字符b,选择b 对应的区间0.3333 - 0.6667。
这时由于多了字符b,三个字符的概率分布变成:Pa = 1/4,Pb = 2/4,Pc = 1/4。
再按照新的概率分布比例划分0.3333 - 0.6667 这一区间,划分的结果可以用图形表示为:+-- 0.6667 Pc = 1/4 | +-- 0.5834 | | Pb = 2/4 | | | +-- 0.4167 Pa = 1/4 | +-- 0.3333接着字符c,上一步中得到的 c 的区间0.5834 - 0.6667。
p算法,k算法,破圈法,穷举法,ew算法,d算法,bf算法,fw算法的基本原理和应用场合 -回复

p算法,k算法,破圈法,穷举法,ew算法,d算法,bf算法,fw算法的基本原理和应用场合-回复这是一篇关于几种常见算法的基本原理和应用场合的文章,我们将一一回答你提出的问题。
首先,让我们来了解一下最常见的算法之一——穷举法。
穷举法的基本原理是通过遍历所有可能的解空间,从中找到满足条件的解。
它的应用场合包括但不限于密码破解、密码学中的攻击问题、组合问题、排列问题等。
接下来,我们来介绍下破圈法。
破圈法是一种用于解决循环链表中环的问题的算法。
它的基本原理是使用快慢指针来检测链表中是否存在环,如果存在环,则通过慢指针每次向前移动一步,快指针每次向前移动两步的方式,最终两个指针会相遇于环的起点。
因此,破圈法的应用场合主要是解决链表中环的问题,例如判断链表是否有环、找到环的起点等。
下一种算法是ew算法。
ew算法的全称是Exponent Weighted algorithm,是一种加权指数算法。
这个算法的基本原理是通过对历史数据进行加权取值,使得最新数据的权重更高,从而反映最新数据的变化情况。
它的应用场合主要是用于计算带有时间概念的数据的指数平滑移动平均值,例如股票价格的预测、网络流量的预测等。
接下来,让我们来介绍一下d算法。
d算法是一种图搜索算法,用于解决有向图的单源最短路径问题。
它的基本原理是通过迭代更新节点的距离值,直到找到从源节点到目标节点的最短路径为止。
d算法的应用场合包括路由选择、网络优化、数据挖掘等。
接下来,我们来介绍bf算法。
bf算法的全称是Bellman-Ford算法,它是一种用于解决带有负权边的图的单源最短路径问题的算法。
bf算法的基本原理是通过反复松弛边的操作来逐步更新节点的距离值,直到找到从源节点到目标节点的最短路径为止。
bf算法的应用场合主要是解决带有负权边的网络中的路由选择问题,例如计算机网络中的数据包路由等。
最后,让我们来介绍一下fw算法。
fw算法的全称是Floyd-Warshall算法,它是一种用于解决带有负权边的有向图的多源最短路径问题的算法。
GMSK调制解调原理和应用
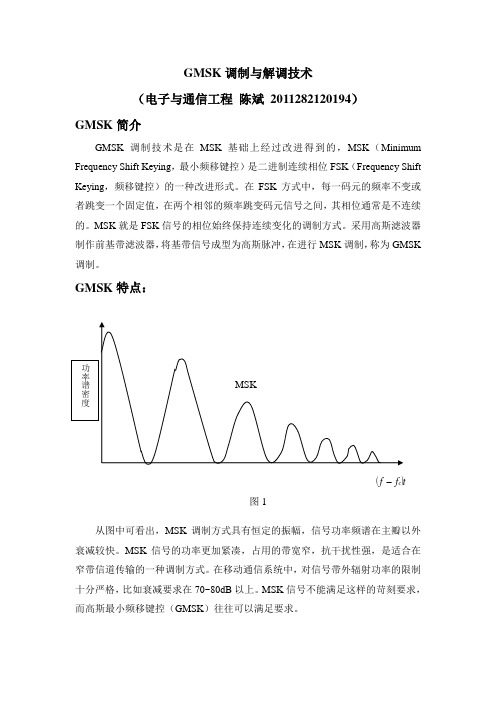
GMSK调制与解调技术(电子与通信工程陈斌2011282120194)GMSK简介GMSK调制技术是在MSK基础上经过改进得到的,MSK(Minimum Frequency Shift Keying,最小频移键控)是二进制连续相位FSK(Frequency Shift Keying,频移键控)的一种改进形式。
在FSK方式中,每一码元的频率不变或者跳变一个固定值,在两个相邻的频率跳变码元信号之间,其相位通常是不连续的。
MSK就是FSK信号的相位始终保持连续变化的调制方式。
采用高斯滤波器制作前基带滤波器,将基带信号成型为高斯脉冲,在进行MSK调制,称为GMSK 调制。
GMSK特点:()t f-f c图1从图中可看出,MSK调制方式具有恒定的振幅,信号功率频谱在主瓣以外衰减较快。
MSK信号的功率更加紧凑,占用的带宽窄,抗干扰性强,是适合在窄带信道传输的一种调制方式。
在移动通信系统中,对信号带外辐射功率的限制十分严格,比如衰减要求在70~80dB以上。
MSK信号不能满足这样的苛刻要求,而高斯最小频移键控(GMSK)往往可以满足要求。
GMSK 调制GMSK 调制的一般原理MSK 调制是调制指数为0.5的二进制调频,其基带信号为矩形波形。
为了压缩MSK 信号的功率,可在MSK 调制前加入高斯低通滤波器,称为预调制滤波器。
对矩形进行滤波后,得到一种新型的基带波形,使其本身和尽可能高阶的导数连续,从而得到较好的频谱特性。
GMSK 调制原理方框图如下所示。
输出 为了有效地抑制MSK 的带外辐射并保证进过预调制滤波后的已调信号能采用简单的MSK 相干检测电路,预调制滤波器必须具有以下特性:1.带宽窄并且具有陡峭的截止特性;2.冲击响应的过冲较小;3.滤波器输出脉冲面积为一常量,该常量对应的一个码元内的载波相移为2π。
其中,条件1是为了抑制高频分量;条件2是为了防止过大的瞬时频偏;条件3是为了使调制指数为0.5.高斯低通滤波器的传输函数为()⎪⎭⎫ ⎝⎛=-fa f H 22exp (1.1)式中,a 是与高斯滤波器的3dB 带快b B 有关的一个常数。
算术编码工作原理

算术编码工作原理在给定符号集和符号概率的情况下,算术编码可以给出接近最优的编码结果。
使用算术编码的压缩算法通常先要对输入符号的概率进行估计,然后再编码。
这个估计越准,编码结果就越接近最优的结果。
例: 对一个简单的信号源进行观察,得到的统计模型如下:∙60% 的机会出现符号中性∙20% 的机会出现符号阳性∙10% 的机会出现符号阴性∙10% 的机会出现符号数据结束符. (出现这个符号的意思是该信号源'内部中止',在进行数据压缩时这样的情况是很常见的。
当第一次也是唯一的一次看到这个符号时,解码器就知道整个信号流都被解码完成了。
)算术编码可以处理的例子不止是这种只有四种符号的情况,更复杂的情况也可以处理,包括高阶的情况。
所谓高阶的情况是指当前符号出现的概率受之前出现符号的影响,这时候之前出现的符号,也被称为上下文。
比如在英文文档编码的时候,例如,在字母Q 或者q出现之后,字母u出现的概率就大大提高了。
这种模型还可以进行自适应的变化,即在某种上下文下出现的概率分布的估计随着每次这种上下文出现时的符号而自适应更新,从而更加符合实际的概率分布。
不管编码器使用怎样的模型,解码器也必须使用同样的模型。
一个简单的例子以下用一个符号串行怎样被编码来作一个例子:假如有一个以A、B、C三个出现机会均等的符号组成的串行。
若以简单的分组编码会十分浪费地用2 bits来表示一个符号:其中一个符号是可以不用传的(下面可以见到符号B正是如此)。
为此,这个串行可以三进制的0和2之间的有理数表示,而且每位数表示一个符号。
例如,“ABBCAB”这个串行可以变成0.011201(base3)(即0为A, 1为B, 2为C)。
用一个定点二进制数字去对这个数编码使之在恢复符号表示时有足够的精度,譬如0.001011001(base2) –只用了9个bit,比起简单的分组编码少(1 – 9/12)x100% = 25%。
这对于长串行是可行的因为有高效的、适当的算法去精确地转换任意进制的数字。
iq信号fsk psk调制算法

FSK (Frequency Shift Keying,频移键控) 和PSK (Phase Shift Keying,相移键控) 是两种常见的数字调制算法,用于将数字信号调制成模拟信号。
下面分别介绍FSK 和PSK 的调制算法。
1. FSK (Frequency Shift Keying) 调制算法:
FSK 是一种通过改变载波频率来传输数字信息的调制技术。
在FSK 中,不同的数字值被映射到不同的频率,以传输二进制数据。
FSK 调制算法的基本步骤如下:
- 确定两个不同频率的载波信号,通常分别代表二进制数字0 和1。
- 对要调制的数字信号进行编码,将二进制0 和1 映射到对应的频率值。
- 将编码后的数字信号与载波信号相乘得到调制后的信号。
2. PSK (Phase Shift Keying) 调制算法:
PSK 通过改变载波相位的方式来传输数字信息。
在PSK 中,不同的数字值被映射到不同的相位,以传输二进制数据。
PSK 调制算法的基本步骤如下:
- 确定多个相位值,通常为0°、90°、180°、270°,分别代表二进制数字00、01、10、11。
- 对要调制的数字信号进行编码,将二进制数字映射到对应的相位值。
- 将编码后的数字信号与载波信号相乘得到调制后的信号。
这些是FSK 和PSK 调制算法的基本步骤,具体实现可能因使用的编程语言和使用的调制器件而有所差异。
在实际应用中,还可能需要考虑调制器件的特性、误码率控制等因素。
p算法,k算法,破圈法,穷举法,ew算法,d算法,bf算法,fw算法的基本原理和应用场合

P算法,也称为顺序取端的谱列姆(Prim)算法,其基本原理是在无向图中任取一端作为起始点,置邻接阵为全零阵。
然后选取一个顶点Vj1,作子图G1={Vj1}。
接着比较G1到G-G1中各边长度,取最小的。
把所连接端Vj2并入G1得G1 = {Vj1,Vj2}。
如此迭代下去,可以得到最终的树状结构。
K算法的主要步骤是使用并查集数据结构,将边权值排序,然后从权值最小的边开始考察,依次考察权值依次变大的边。
每考察一条边,就要考虑这条边的两个顶点是否已经在同一个集合中,若没有,则将这两个顶点所在的集合进行合并。
考察完所有的边之后,就可以得到最小生成树的集合。
破圈法主要用于解决最小生成树问题,其基本思想是在每一步选择一条最短的边,并尝试将其加入最小生成树中,同时检查是否会形成环。
如果会形成环,则不选择这条边;否则,将该边加入最小生成树中。
穷举法的基本思想是在可能的解空间中穷举出每一种可能的解,并对每一个可能解进行判断,从中筛选出问题的答案。
这种方法的关键步骤是划定问题的解空间,并在该解空间中一一枚举每一种可能的解。
FSK解码原理及实现方法

FSK解码原理及实现方法1.解码数学原理条件:FSK的频率为:1200/2200-->1/0;wc = 1700,即(1200+2200)/2,设delta = +500/-500;T是采样周期则:1200 可表示为cos((wc-delta)*t);2200 可表示为cos((wc+delta)*t);设第n次采样值为cos((wc+/-delta)*(t-T)),第n+1采样值为cos((wc+/-delta)*t).有:value(n)*value(n+1) =cos((wc+/-delta)*t)*cos((wc+/-delta)*(t-T))= [cos((wc+/-delta)*t+(wc+/-delta)*(t-T))+cos((wc+/-delta)*t-(wc+/-delta)*(t- T))]/2= [cos(2*(wc+/-delta)*t-(wc+/-delta)*T) + cos((wc+/-delta)*T)]/2(1)(H) (L)将(1)式通过一个低通滤波器,则(1)式的(H)项即2位频率被滤掉,只剩下(L)项: (1)--->Lowpass filter--->cos((wc+/-delta)*T)再看:cos((wc+/-delta)*T) = cos(wc*T+/-delta*T) (2)IF: wc*T = PI/2则cos(wc*T+/-delta*T) = cos(PI/2+/-delta*T)= -/+sin(delta*T) (3)(3)式则是FSK的值,2.滤波器.对于来电显示,下面这段程序可以达到解码的要求定义:#define FSKBUF 4byte g_cADCResult;//A/D的采样值int currentx,currenty,lastx,last_sample;int g_iFSKBuf[FSKBUF];int g_iFSKAvg;int g_iFSKBuf1[FSKBUF];int g_iFSKAvg1;int g_iFSKBuf2[FSKBUF];int g_iFSKAvg2;byte g_cFSKBufPoint;//在滤波之前将变量初化为0程序实现:(每次采样要做以下工作,注意采样频率和CID的波特率不是倍数关系currentx = g_cADCResult;currenty = last_sample;last_sample = currentx;//last sample in currenty,now sample in currenx; currenty *= currentx;//cos(t)*cos(t-T) = -/+sin(delta*T); //------avg--lowpass filter;g_iFSKAvg -= g_iFSKBuf[g_cFSKBufPoint];g_iFSKBuf[g_cFSKBufPoint] = currenty;g_iFSKAvg += currenty;currenty = g_iFSKAvg;//---------end filter;g_iFSKAvg1 -= g_iFSKBuf1[g_cFSKBufPoint];g_iFSKBuf1[g_cFSKBufPoint] = currenty;g_iFSKAvg1 += currenty;currenty = g_iFSKAvg1;//second filter overg_iFSKAvg2 -= g_iFSKBuf2[g_cFSKBufPoint];g_iFSKBuf2[g_cFSKBufPoint] = currenty;g_iFSKAvg2 += currenty;currenty = g_iFSKAvg2;//third filter overg_cFSKBufPoint++;g_cFSKBufPoint %= FSKBUF;if(currenty>0){//接收到bit 1}else{//接收到bit 0}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FGK算法编码过程
1. 引言
FGK算法(Fenwick-Greedy-Kruskal algorithm)是一种常用于数据压缩和编码的
算法。
它是一种基于字典树的前缀编码算法,通过将出现频率较高的字符用较短的二进制码表示,从而实现对数据进行压缩。
在本文中,我们将详细介绍FGK算法的编码过程,并给出相应的示例。
2. FGK算法概述
FGK算法通过构建一颗字典树(也称为前缀树或者Trie树)来实现对数据的编码。
字典树是一种多叉树,其中每个节点代表一个字符或者字符序列,并且从根节点到任意一个叶子节点所经过的路径上所代表的字符序列唯一。
FGK算法主要包含两个步骤:初始化和编码。
在初始化阶段,构建初始的字典树。
在编码阶段,遍历输入数据,并通过字典树将每个字符映射为相应的二进制码。
3. FGK算法初始化
在初始化阶段,我们需要构建初始的字典树。
首先创建一个空节点作为根节点。
然后遍历输入数据中每个字符,并按照以下规则插入到字典树中: - 如果字符已存
在于字典树中,则什么都不做。
- 如果字符不存在于字典树中,则将字符插入到
字典树的合适位置,并为该节点创建一个唯一的编号(用于后续编码时使用)。
以下是FGK算法初始化的示例:
输入数据: abracadabra
初始字典树:
root
/ \
a(1) b(2)
/ \
b(3) r(4)
/ \ \
r(5) d(6) a(7)
/ \
c(8) d(9)
/ \
a(10) b(11)
4. FGK算法编码
在编码阶段,我们需要遍历输入数据,并通过字典树将每个字符映射为相应的二进制码。
具体步骤如下: 1. 初始化空字符串code,用于存储编码结果。
2. 遍历输入数据中的每个字符: - 在字典树中查找当前字符对应的节点。
- 将该节点的编号转换为二进制,并将其添加到code末尾。
3. 返回最终的编码结果code。
以下是对输入数据”abracadabra”进行FGK算法编码的示例:
输入数据: abracadabra
编码结果:
a -> 01
b -> 10
r -> 11
a -> 01
c -> 001
a -> 01
d -> 000
a -> 01
b -> 10
r -> 11
a -> 01
最终编码结果: 0110010101000100011011010110010101
5. 总结
在本文中,我们介绍了FGK算法的编码过程。
该算法通过构建字典树,并将出现频率较高的字符用较短的二进制码表示,从而实现对数据的压缩。
FGK算法的编码过程包括初始化和编码两个步骤,其中初始化阶段构建初始的字典树,编码阶段通过字典树将每个字符映射为相应的二进制码。
希望本文能够对你理解FGK算法的编码过程有所帮助!。
