信号与系统电子教案(3版.本.燕 (22)
信号与系统电子教案(3)_绪论(3)(本科2013)

(3)把各个阶数降低了的导数及输出函数分别通过各自 的标量乘法器,一起与输入函数相加,加法器的输出就 是最高阶导数。
第六节系统模型及其分类
二、系统的数学模型和框图模型
4.构造系统模拟图的一般规则
n阶系统
y ( n ) (t ) a n 1 y ( n 1) (t ) a1 y ' (t ) a 0 y x (t ) y ( n ) (t ) x (t ) a n 1 y ( n 1) (t ) a1 y ' (t ) a 0 y
是一种理想的系统。(如以后要讲的理想滤波器)
第六节系统模型及其分类
三、系统模型分类
8.稳定系统与非稳定系统
一个系统,若对有界的激励f(.)所产生的响应yf(.)也是有 界时,则称该系统为有界输入有界输出稳定,简称稳定。 即若│f(.)│<∞,其│yf(.)│<∞ 则称系统是稳定的。
本课程主要研究:集中参数的、线性非时变的 连续时间和离散时间系统(线性时不变,linear time-invariant,缩写为LTI),以后简称LTI系统。
信号与系统
Signals and Systems
郑州大学物理工程学院 电子科学与仪器实验中心 赵书俊 Tel:67780976 Email:zhaosj@
绪
论
第一章 绪 论
信号与系统
信号的描述、分类和典型示例 连续时间信号的运算 阶跃信号与冲激信号 信号的分解
正交函数分量 利用分形理论描述信号
第五节信号的分解
一、直流分量与交流分量
f (t ) f D f A (t )
《信号与系统教案》课件

《信号与系统教案》PPT课件第一章:信号与系统概述1.1 信号的概念与分类定义:信号是自变量为时间(或空间)的函数,用于描述物理量或信息。
分类:模拟信号、数字信号、离散信号、连续信号等。
1.2 系统的概念与分类定义:系统是由输入信号、系统本身和输出信号三部分组成的。
分类:线性系统、非线性系统、时不变系统、时变系统等。
第二章:信号的运算与处理2.1 信号的运算加法、减法、乘法、除法等基本运算。
叠加原理与分配律。
2.2 信号的处理滤波器、放大器、采样与量化等。
第三章:线性时不变系统的性质3.1 齐次性定义:若系统对于任意输入信号f(t),其输出信号y(t)都满足y(t)=af(t),则称系统为齐次系统。
3.2 叠加性定义:若系统对于两个输入信号f1(t)和f2(t)的输出信号y1(t)和y2(t)满足y1(t)+y2(t)=a(f1(t)+f2(t)),则称系统为叠加系统。
3.3 时不变性定义:若系统对于任意输入信号f(t),其输出信号y(t-t0)与输入信号f(t-t0)的输出信号y(t)相同,则称系统为时不变系统。
第四章:傅里叶级数与傅里叶变换4.1 傅里叶级数定义:将周期信号分解为正弦、余弦信号的和。
傅里叶级数的展开与系数计算。
4.2 傅里叶变换定义:将信号从时域转换到频域。
傅里叶变换的性质与计算方法。
第五章:拉普拉斯变换与Z变换5.1 拉普拉斯变换定义:将信号从时域转换到复频域。
拉普拉斯变换的性质与计算方法。
5.2 Z变换定义:将信号从时域转换到离散域。
Z变换的性质与计算方法。
第六章:信号与系统的时域分析6.1 系统的时域响应定义:系统对输入信号的响应称为系统的时域响应。
系统的时域响应的计算方法。
6.2 系统的稳定性定义:系统在长时间内能否收敛到一个稳定状态。
判断系统稳定性的方法。
第七章:信号与系统的频域分析7.1 傅里叶变换的应用频谱分析:分析信号的频率成分。
滤波器设计:设计线性时不变系统的滤波器。
信号与系统_郑君里_第三版_课件资料

2017/10/8
6
积分器:
R
C vo ( t )
微分器: C
vi(t)
vi(t)
R
vo ( t )
电视系统:
黑灰白 消息 变换器 发射机 信道 (空间) 接收机 变换器
黑灰 白 消息
(图像) (摄像机)
(显像管) (图像)
2017/10/8
7
1.2 信号分类和典型信号
1.2.1 信号的分类
对于各种信号,可以从不同角度进行分类。
2017/10/8
1.2.3 奇异信号
在信号与系统分析中,经常要遇到函数本身有不连续 点或其导数与积分有不连续点的情况,这类函数统称为奇 异函数或奇异信号。 一、单位斜变信号 斜变信号指的是从某一时刻开始随时间正比例增长的 信号。其表示式为
R(t ) t , (t 0)
R(t) 1 0 1 t
sin t Sa (t ) t
Sa (t )
1
2
2017/10/8
2
t
12
Sa (t )
1
2
2
t
Sa t 的性质:
(1) Sa t 是偶函数,在 t 正负两方向振幅都逐渐 衰减。 (2)
0
Sa(t )dt
2
Sa(t ) dt
13
2017/10/8 4
1.1 引论
信号:一种物理量(电、光、声)的变化。
消息:待传送的一种以收发双方事先约定的方式组成的符号,
如语言、文字、图像、数据等。
电信号:与消息(语言、文字、图像、数据)相对应的变化的电流或
信号与系统教案 温艳老师

8/3 ,它的周期为N= M(2π/ β) ,N = 8 (M=3) (2)sin(2k) 的数字角频率为 β1 = 2 rad;由于2π/ β1 = π为无理数, 故f2(k) = sin(2k)为非周期序列 。 (3)sin(3πk/4) 和cos(0.5πk)的数字角频率分别为 β1 = 3π/4 rad, β2 = 0.5π rad 由于2π/ β1 = 8/3, 2π/ β2 = 4为有理数,故它们的周期分别为N1 = 8 , N1 = 4,故f1(k) 为周期序列,其周期为N1和N2的最小公倍数8。
f(k)= {…,0,1,2,-1.5,2,0,1,0,…} ↑ k=0
第20页
通常将对应某序号m的序列值称为第m个样点的“样值”
■
信号与系统
1.1.1 信号的分类
3. 周期信号和非周期信号
周期信号(period signal)是定义在(-∞,∞)区 间,每隔一定时间T (或整数N),按相同规律重复 变化的信号。 连续周期信号f(t)满足 f(t) = f(t + mT),m = 0,±1,±2,… 离散周期信号f(k)满足 f(k) = f(k + mN),m = 0,±1,±2,… 满足上述关系的最小T(或整数N)称为该信号的周期。 不具有周期性的信号称为非周期信号。
上启下的作用 。
第4页
■
信号与系统
课程特点
• 与《电路分析》比较,更抽象,更一般化; • 应用数学知识较多,用数学工具分析物理概念;
(信号与系统课程的核心,是教会我们如何利用数学工
具,解决实际工程问题)
• 主要工具: 微分、积分、线性代数、复变函数、微分方 程 、差分方程;
第5页
■
信号与系统
信号与系统电子教案(3版.本.燕 (4)

2、系统的分类
连续系统 离散系统 混合系统 串联系统 并联系统 反馈系统
信号与系统 1.3-3
系统的串联 系统的并联 系统的反馈连接
图3
3、线性时不变系统
线性系统与非线性系统
信号与系统 1.3-4
若f1( t ) y1( t ),f2( t ) y2( t ) 则对于任意常数a1和a2,有
a1 f1( t ) + a2 f2( t ) a1 y1( t ) + a2 y2( t ) 则为线性系统。
非线性系统不满足上述齐次性和可加性。
信号与系统 1.3-5
4、线性系统的特性:
微分特性:若f ( t ) y( t ),则 f (t) y(t)
积分特性:若f ( t ) y( t ),则
信号与系统 1.3-7
图4 时不变特性示意图
线性时不变系统(LTI): 系统既是线性的,又是时不变的; 或系统的方程为线性常系数微分方程。
信号与系统 1.3-86、因 Nhomakorabea系统与非因果系统
因果系统:在激励信号作用之前系统不产生响应。 否则为非因果系统。
图5
信号与系统 1.3-9
7、系统分析: 建立模型(数学) 时域分析 频域(变换域)分析 系统特性
单输入---出系统 与多输入---出系统
end
t
t
0 f ( )d 0 y( )d
频率保持性:信号通过线性系统后不会产生新的频
率分量。 尽管各频率分量的大小和相位可能发生
变化。
信号与系统 1.3-6
5、时不变系统与时变系统
时不变系统:系统的元件参数不随时间变化; 或系统的方程为常系数。 否则为时变系统。
信号与系统电子教案
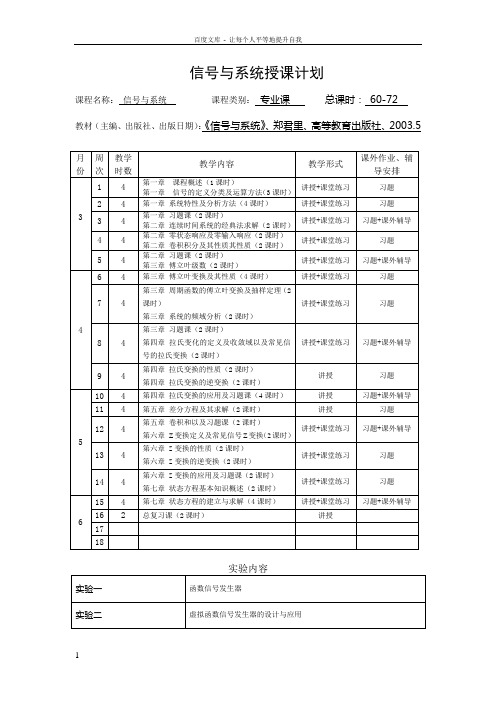
信号与系统授课计划课程名称:信号与系统课程类别:专业课总课时:60-72教材(主编、出版社、出版日期):《信号与系统》、郑君里、高等教育出版社、2003.5第一章绪论(8-10课时)本章是信号与系统课程的总论,包括信号与系统课程概述和一些基本概念,简单来说就是要讲清楚什么是信号、什么是系统、以及信号与系统之间是什么关系的问题。
主要内容包括:信号与系统课程概述、信号与系统课程的主要内容、信号的定义及常见信号介绍以及信号的运算、系统的定义与分类以及系统的分析方法介绍等。
本章内容是全书内容的浓缩、是基础、是引言,所以非常重要。
一、主要知识点如下:1、信号与系统课程概述主要包括:(1)信号与系统课程的产生与发展(2)信号与系统课程与其他课程的联系(3)信号与系统的应用领域2、信号的定义与分类、信号的运算主要包括:(1)信号的定义与分类(2)信号的运算3、系统的定义、分类及分析方法主要包括:(1)系统的定义及分类(2)线性时不变系统四大特性及判断方法二、本章知识重难点分析1、信号的定义及分类是重点,其中关于周期信号的定义及信号周期的计算是难点,同样关于连续时间信号与离散时间信号的定义与区别也是难点。
2、几种特殊信号的定义是本课程的重点内容,包括单位阶跃信号、单位冲激信号的定义与运算。
其中单位阶跃信号与单位冲激信号的定义与性质是难点。
3、信号的运算也是本章知识的重点内容,特别是信号直流分量与交流分量、信号奇分量与偶分量等的分解运算,信号的尺度、位移、反折运算等。
4、系统的定义及分类是重点5、线性时不变系统的定义及四大特性,其中四大特性(微积分、时不变、线性、因果性)的定义与判断是难点,特别是线性性是非常重要的内容。
6、线性时不变系统的分析方法是本章的重点7、系统的描述方法,框图与方程,框图与方程之间的关系与转换方法,其中框图与方程之间的转换关系是难点。
三、本章知识点课时安排1、信号与系统课程概述(2课时)2、信号的定义与分类、信号的运算(3课时)3、系统的定义、分类及分析方法(3课时)第二章连续时间系统的时域分析(6-8课时)LTI连续系统的时域分析过程可以理解为建立并求解线性微分方程,因其分析过程涉及的函数变量均为时间t,故称为时域分析法。
信号与系统电子教案 (3)

第3章 信号与系统的频域分析
引言:
有小则有大,有分则有合; 有之以为利,无之以为用。 信号各有异,频域是灵魂。
学习重点:
• 周期信号分解为三角级数和指数形式; • 周期信号频谱的特点; • 非周期信号的频谱函数; • 信号的频带宽度; • 傅氏变换的性质和应用。
• 系统的频率特性(系统函数); • 不失真传输条件; • 信号通过低通滤波器; • 采样定理及其应用; • 频分复用与时分复用。
信号与系统电子教案

信号与系统讲课打算课程名称:信号与系统课程类别:专业课总课时:60-72教材(主编、出版社、出版日期):《信号与系统》、郑君里、高等教育出版社、2003.5实验内容第一章绪论(8-10课时)本章是信号与系统课程的总论,包括信号与系统课程概述和一些大体概念,简单来讲确实是要讲清楚什么是信号、什么是系统、和信号与系统之间是什么关系的问题。
要紧内容包括:信号与系统课程概述、信号与系统课程的要紧内容、信号的概念及常见信号介绍和信号的运算、系统的概念与分类和系统的分析方式介绍等。
本章内容是全书内容的浓缩、是基础、是引言,因此超级重要。
一、要紧知识点如下:一、信号与系统课程概述要紧包括:(1)信号与系统课程的产生与进展(2)信号与系统课程与其他课程的联系(3)信号与系统的应用领域二、信号的概念与分类、信号的运算要紧包括:(1)信号的概念与分类(2)信号的运算3、系统的概念、分类及分析方式要紧包括:(1)系统的概念及分类(2)线性时不变系统四大特性及判定方式二、本章知识重难点分析一、信号的概念及分类是重点,其中关于周期信号的概念及信号周期的计算是难点,一样关于持续时刻信号与离散时刻信号的概念与区别也是难点。
二、几种特殊信号的概念是本课程的重点内容,包括单位阶跃信号、单位冲激信号的概念与运算。
其中单位阶跃信号与单位冲激信号的概念与性质是难点。
3、信号的运算也是本章知识的重点内容,专门是信号直流分量与交流分量、信号奇分量与偶分量等的分解运算,信号的尺度、位移、反折运算等。
4、系统的概念及分类是重点五、线性时不变系统的概念及四大特性,其中四大特性(微积分、时不变、线性、因果性)的概念与判定是难点,专门是线性性是超级重要的内容。
六、线性时不变系统的分析方式是本章的重点7、系统的描述方式,框图与方程,框图与方程之间的关系与转换方式,其中框图与方程之间的转换关系是难点。
三、本章知识点课时安排一、信号与系统课程概述(2课时)二、信号的概念与分类、信号的运算(3课时)3、系统的概念、分类及分析方式(3课时)第二章持续时刻系统的时域分析(6-8课时)LTI持续系统的时域分析进程能够明白得为成立并求解线性微分方程,因其分析进程涉及的函数变量均为时刻t,故称为时域分析法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 电路的微分方程为
信号与系统 4.4-4
对方程两边取拉普拉斯变换,有
sUC (s) uC (0 ) 2UC (s) 2
式中,UC(s)为uC(t)对应的象函数。把uC(0-) =2代入方程,则有 UC (s)(s 2) 4
即
UC
(s)
s
4
2
取反变换得
h(t) uC (t) 4e2t (t)
将在电感两端产生高压,由高压打火点燃汽油而发 动。设R=2,L=1H,C=0.25F,试求t 0时的电 压uL(t)及其最大值。
图8
信号与系统 4.4-15
解 首先做电路的s域模型,如图8(c)所示。其中 起始状态
iL
(0
)
12 2
A
6A
uC (0 ) 0
由网孔方程可得
I
(s)
12 s
LiL
(0
信号与系统 4.4-5
例
设有RLC串联电路,输人uS(t)=δ(t),电路的初始状态
为零。设L=1 H,C=1/3F,R=4Ω,以uC(t)为输出,
求冲激响应h(t)。
图3 解 由电路可得微分方程
信号与系统 4.4-6
即 代人数据得 对上式两边取拉普拉斯变换,利用微分性质,得
从而有 利用部分分式展开法得
因 uC( 0 ) = 2V,则方程的拉氏变换为
RI
(s)
L[sI
(s)
i(0 )]
uc (0 ) s
I (s) sC
10 s
信号与系统 4.4-8
得电流象函数
反变换得
I
(s)
10 s
Li(0
)
uc
(0 s
)
R sL 1
sC
8
s2 10s 250
i(t) 8 e5t sin(15t) (t)
sy(0 )
y(0 )]
3[sY (s)
y(0 )]
2Y (s)
s
1
3
即
Y (s) s2 8s 6 (s 1)(s 2)(s 3)
展开分式确定系数后,有
y(t) = L1[Y(s)]=4.5et 4e2t + 0.5e3t ( t 0 )
信号与系统 4.4-3
例 如图2所示的RC电路,设uC(0-)=2V,试求响应u C(t)。图中 R=1Ω,C=0.5F 。
图6
➢ 电感元件
u(t) L di(t) dt
取变换
U (s) sLI (s) Li(0 )
或 I (s) 1 U (s) i(0 )
sL
s
信号与系统 4.4-11
图7
信号与系统 4.4-12
➢ 基氏定律和S域阻抗(导纳)
KCL : I (s) 0 KVL : U (s) 0
阻抗:
Z(s) U(s) I (s)
导纳:
Y(s) 1 I(s) Z(s) U (s)
ZR (s) R
ZL (s) sL
ZC (s)
1 sC
正弦稳态与复频域分析的对比:
信号与系统 4.4-13
➢ S域模型应用
信号与系统 4.4-14
例 图8(a)为某汽车点火系统的电路模型,12V电源为 汽车蓄电池,L为点火线圈。当开关在t = 0断开时,
4.4 系统的S域分析
1、 微分方程的S域求解
思想:
信号与系统 4.4-1
取变换
时域模型
S域模型
反变换
解S域方程
时域响应
图1
信号与系统 4.4-2
例 设有方程
y(t) 3y(t) 2y(t) e3t , t 0
y(0) 1, y(0) 2, 求y(t)当 t ms 时,电感电压达最大值为
4
uLmax 12000V
end
)
R sL 1
2
12 6 s s 106
sC
0.25s
6s 12 6s 12 s2 2s 20002 s2 20002
s2
6s 20002
信号与系统 4.4-16
反变换得
i(t) 6cos(2000t) (t 0)
故有
uL (t)
L
di dt
12000sin(2
000t)
取上式的反变换,得冲激响应
信号与系统 4.4-7
例 对于图4所示电路,已知R = 10Ω,L = 1H,C =
0.004F,求i ( t )。
L
解 其KVL方程为
图4
Ri(t)
L
di(t) dt
uc
(0 )
1 C
t
i( )d
0
10
令 i( t ) I( s ), u( t ) U( s ),i( 0 ) = 0,
15
2、 电路的S域模型与应用
➢ 电阻元件
u(t) Ri(t) 取变换
U (s) RI (s)
信号与系统 4.4-9
图5
➢ 电容元件
i(t) C du(t) dt
取变换
I (s) sCU (s) Cu(0 )
或 U (s) 1 I (s) u(0 )
sC
s
信号与系统 4.4-10
