第1讲:数与式-义
第一讲数与式

第一讲数与式作者:王宗俊来源:《初中生·考试》2012年第05期数与式的内容包括:实数的有关概念及其运算、代数式、整式、分式以及二次根式?郾在中考数学试卷中,一般有4~6道题,分值所占比例在10%~15%?郾现以2011年中考题为例,对这部分内容作归类解析?郾考点1 正数、负数及其应用例1 (2011年贵阳卷)如果“盈利10%”记为+10%,那么“亏损6%”记为()?郾A?郾 -16%?摇?摇 B?郾 -6%?摇?摇 C?郾 +6%?摇?摇 D?郾 +4%分析:正数和负数可以表示一对相反意义的量,“盈利”和“亏损”是一对相反意义的量,既然盈利用正数表示,那么亏损就用负数来表示,后面的百分比的值不变,即-6%?郾选B?郾温馨小提示:用正数和负数表示相反意义的量时,哪种意义为正,是可以任意选择的,但习惯上把“前进、上升、收入、零上温度等”规定为正,而把“后退、下降、支出、零下温度等”规定为负?郾考点2 实数的分类例2 (2011年滨州卷)在实数π、■、■、sin30°中,无理数的个数为().A?郾 1?摇 B?郾 2?摇 C?郾 3 D?郾 4解:sin30°=■,所以只有π和■是无理数?郾选B?郾温馨小提示:一个实数不是有理数,就是无理数?郾而初中阶段常见的无理数有以下三种类型:(1)带根号且开方开不尽的方根,如■、■等;(2)像循环但是不循环的无限小数,如0?郾30300300030000…(两个3之间依次多一个0);(3)含有π的数,如2π,π+3,5π-1等?郾考点3 相反数、倒数、绝对值例3 (2011年益阳卷)-2的相反数是()?郾A?郾 2?摇?摇 B?郾 -2?摇?摇 C?郾■?摇?摇 D?郾-■解:只有符号不同的两个数叫做互为相反数?郾选A?郾例4 (2011年长沙卷)|-2|等于().A?郾 2?摇?摇 B?郾 -2?摇?摇 C?郾■?摇?摇 D?郾 -■解:选A?郾例5 (2011年泰州卷)-3的倒数为()?郾A?郾 -3?摇?摇 B?郾■?摇?摇 C?郾 3?摇?摇 D?郾 -■解:选D.温馨小提示:相反数、倒数、绝对值是中考常见题.考点4 近似数、有效数字与科学记数法例6 (2011年北京卷)我国第六次全国人口普查数据显示,居住在城镇的人口总数达到665 575 306人?郾将665 575 306用科学记数法表示(保留三个有效数字)约为()?郾A?郾 66?郾6×107?摇?摇 B?郾 0?郾666×108?摇?摇 C?郾 6?郾66×108?摇?摇 D?郾 6?郾66×107解:665 575 306=6?郾655 753 06×108≈6?郾66×108?郾选C?郾温馨小提示:科学记数法与近似数(有效数字的确定)是历年中考的热点,在确定a×10n 中n的值时,不要数错了整数位和0的个数?郾近年来将带单位(万、亿)的数改写成科学记数法的题比较常见. 当近似数所要保留的数位较大时,一般先写成科学记数法的形式,然后再按要求取近似值?郾考点5 数轴及实数大小的比较例7 (2011年贵阳卷)如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB为半径画弧,交正半轴于一点,则这个点表示的实数是()?郾A?郾 2?郾5?摇?摇 B?郾2■?摇?摇C?郾■?摇?摇 D?郾■解:由勾股定理可知,OB=■=■. ∴选D?郾温馨小提示:实数和数轴是一一对应的关系,比较实数大小的方法有两种:(1)利用数轴比较实数的大小时,在数轴上右边的数总比左边的数大;(2)根据数的性质比较大小时,正数都大于0,负数都小于0,两个正数比较,绝对值大的数大;两个负数比较大小,绝对值大的反而小?郾考点6 平方根、算术平方根、立方根例8 (2011年毕节卷)■的算术平方根是()?郾A?郾 4?摇?摇 B?郾 ±4?摇?摇 C?郾 2?摇?摇 D?郾 ±2解:∵ ■=4,4的算术平方根是2?郾选C?郾例9 (2011年河南卷)27的立方根是 ?郾解:∵ 33=27,∴ 27的立方根是3?郾温馨小提示:熟练掌握平方根、算术平方根、立方根的概念是解这类题的关键. 在例8中,谨防出现选A或B的错误.考点7 实数的混合运算与估算例10 (2011年桂林卷)计算:(■+1)0-2-1-■tan45°+ |-■|?郾解:原式=1-■-■×1+■=■?郾例11 (2011年徐州卷)估计■的值()?郾A?郾在2到3之间?摇?摇 B?郾在3到4之间C?郾在4到5之间?摇?摇 D?郾在5到6之间解:因为9<(■)2<16,故3<■<4?郾选B?郾温馨小提示:实数的混合运算顺序是先乘方,再乘除,最后算加减,有括号先算括号里面的. 实数运算往往考查零指数幂、负整数指数幂、特殊角的三角函数值?郾零指数幂:a0=1(a≠0),负整数指数幂:a-p=■(a≠0,p为正整数)?郾估算常常要利用完全平方数?郾考点8 列代数式例12 (2011年岳阳卷)将边长分别为■,2■,3■,4■,…的正方形的面积记作S1,S2,S3,S4,…,计算S2-S1,S3-S2,S4-S3,…,若边长为n■(n为正整数)的正方形面积记作S■,根据你的计算结果,猜想Sn+1-Sn=?摇 ?郾解:第n项的边长为n■,第n+1项的边长为(n+1)■,则Sn+1=2(n+1)2,Sn=2n2,则Sn+1-Sn=2(n+1)2-2n2=4n+2?郾温馨小提示:解这类题,需要观察、归纳、验证才能得出结果?郾考点9 整式的运算例13 (2011年桂林卷)下列运算正确的是()?郾A?郾 3x2-2x2=x2?摇?摇 B?郾(-2a)2=-2a2C?郾(a+b)2=a2+b2?摇?摇 D?郾 -2(a-1)=-2a-1解:选A?郾温馨小提示:灵活运用平方差公式、完全平方公式和整式的运算法则是解这类题的关键.考点10 因式分解例14 (2011年随州卷)分解因式8a2-2= ?郾解:原式=8a2-2=2(4a2-1)=2(2a+1)(2a-1)?郾温馨小提示:分解因式的步骤是“一提二套”,若有公因式,先提取公因式,再套用公式分解,要分解到不能再分解为止?郾考点11 分式的值为零与分式无意义例15 (2011年杭州卷)已知分式■,当x=2时,分式无意义,则a= ;当a<6时,使分式无意义的x的值共有个?郾解:当x=2时,分式可化为■,当a-6=0,即a=6时,分式无意义;当x2-5x+a=0时,分式无意义,由于该方程?驻=25-4a,当a<6时,?驻=25-4a>0,所以可以取到两个x的值,使得x2-5x+a=0?郾答案:6,2?郾温馨小提示:分式有意义,则分母不等于0;分式无意义,则分母等于0;分式的值为0,则分子为0且分母不等于0?郾考点12 非负数的性质例16 (2011年达州卷)若■+b2+2b+1=0,则a2+■-|b|= ?郾解:∵ ■+b2+2b+1=0,即■+(b+1)2=0,∴ a2-3a+1=0,b+1=0.∴ a+■=3,即a2+■=7,b=-1?郾∴ a2+■-|b|=7-1=6?郾温馨小提示:几个非负数的和为零,这几个数都为零?郾考点13 分式的化简求值例17 (2011年娄底卷)先化简:(■+■)÷■?郾再从1,2,3中选一个你认为合适的数作为a的值代入求值?郾解:原式=■·■=■·■=■?郾∵ a≠1,a≠-1,a≠0,∴在1,2,3中,a只能取2或3?郾当a=2时,原式=■?郾当a=3时,原式=■?郾注:在a=2,a=3中任选一个算对即可?郾温馨小提示:化简分式,再选取合适的值代入时一定要注意分式有意义,不能取使分母等于0的值?郾■。
初中数学基础知识2第1章《数与式第1节》

方、负整数指数幂、算术平方根、零指数幂、特殊角的三角函数值
第3页
实数的相关概念
1.(2019 山西)-3 的绝对值是
A.-3 B.3
C.-1
3
2.(2016 山西)-1的相反数是
6
A.1 B.-6 C.6
6
3.(2011 山西)|-6|的值是
A.-6
B.-1 C.1
6
6
D.1
3
D.-1
6
D.6
第一章
( C)
A.6.06×104 立方米/时
B.3.136×106 立方米/时
C.3.636×106 立方米/时
D.36.36×105 立方米/时
答案
第5页
第一章
第一节
5.(2017 西)2017年5月18日,我国宣布在南海神狐海域成功试采可 燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计, 仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国 陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为 ( C)
a.186×108吨
b.18.6×109吨
c.1.86×1010 吨
d.0.186×1011 吨
答案
第6页
第一章
第一节
6.(2014 西)pm2.5是指大气中直径小于或等于2.5 μm(1 μm=0.000001 m)的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质, 对人体健康和大气环境质量有很大危害.2.5 μm用科学记数法可表示 为( C )
A.3830×104千瓦
B.383×105千瓦
C.0.383×108千瓦
D.3.83×107千瓦
答案
第 29 页
初中数学中考一轮复习专题1数与式重点、考点知识、方法总结及真题练习
在实数范围内,正数和零统称为非负数.我们已经学习过的非负数有如下三种形式:
(1)仸何一个实数 a 的绝对值是非负数,即| a |≥0; (2)仸何一个实数 a 的平方是非负数,即 a2 ≥0; (3)仸何非负数的算术平方根是非负数,即 a 0 ( a 0 ).
非负数具有以下性质: (1)非负数有最小值零; (2)有限个非负数乊和仍是非负数; (3)几个非负数乊和等于 0,则每个非负数都等于 0. 4.实数的运算
a a (a 0, b 0) bb
②.加减法
将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数丌变,
即合并同类二次根式.
【典例】
1.计算:5 +
﹣×+ ÷.
【答案】 【解析】解:原式= + ﹣
+3 ÷
=2 ﹣1+3
=2 +2.
x xy xy y
2.若 x 0 ,化简
注:单独一个字母戒一个数也是代数式.
2.代数式的分类:
3.代数式的书写规则: (1)数字不字母相乘戒字母不字母相乘,通常把乘号写作“ ”戒省略丌写,字母乊间的
顺序可以交换,但一般按字母表中的先后顺序写.数字应在字母乊前.如: 3b 丌要写成 b3 (2)在代数式中出现除法运算时,一般都变成分数和乘法来计算.如: 2a b 写成 2a
x
2
0
即
x
1 且x 2
2
.
【难度】易
【结束】
2.若
,则 ( )
A. b>3B. b<3C. b≥3D. b≤3
【答案】D.
【解析】
3 b = 3 b ,所以 3 b ≥0,即 b 3 .
1 初三升高一数学暑假 第一讲—数与式(简单,也有必要复习的)

【知识梳理】1.幂的运算性质:①同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,即n m n m a a a +=⋅(m 、n 为正整数);②同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即n m n m a a a -=÷(a≠0,m 、n 为正整数,m>n );③幂的乘方法则:幂的乘方,底数不变,指数相乘,即nnnb a ab =)((n 为正整数);④零指数:10=a (a≠0);⑤负整数指数:nn a a 1=-(a≠0,n 为正整数); 2.整式的乘除法:(1)几个单项式相乘除,系数与系数相乘除,同底数的幂结合起来相乘除. (2)单项式乘以多项式,用单项式乘以多项式的每一个项.(3)多项式乘以多项式,用一个多_项式的每一项分别乘以另一个多项式的每一项. (4)多项式除以单项式,将多项式的每一项分别除以这个单项式.(5)平方差公式:两个数的和与这两个数的差的积等于这两个数的平方, 即22))((b a b a b a -=-+;(6)完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去) 它们的积的2倍,即2222)(b ab a b a +±=±3.分解因式:把一个多项式化成几个整式的积的形式,叫做把这个多项式分解因式.4.分解因式的方法:⑴提公团式法:如果一个多项式的各项含有公因式,那么就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式,这种分解因式的方法叫做提公因式法.⑵运用公式法:公式22()()a b a b a b -=+- ; 2222()a ab b a b ±+=±5.分解因式的步骤:分解因式时,首先考虑是否有公因式,如果有公因式,一定先提取公团式,然后再考虑是否能用公式法分解. 6.分解因式时常见的思维误区:⑴ 提公因式时,其公团式应找字母指数最低的,而不是以首项为准. ⑵ 提取公因式时,若有一项被全部提出,括号内的项“ 1”易漏掉. (3) 分解不彻底,如保留中括号形式,还能继续分解等【例题精讲】 【例1】下列计算正确的是( )A. a +2a=3a 2B. 3a -2a=aC. a 2•a 3=a 6D.6a 2÷2a 2=3a 2【例2】(2008年茂名)任意给定一个非零数,按下列程序计算,最后输出的结果是( )A .mB .m 2C .m +1D .m -1【例3】若2320a a --=,则2526a a +-= .【例4】下列因式分解错误的是()A .22()()x y x y x y -=+- B .2269(3)x x x ++=+ C .2()x xy x x y +=+D .222()x y x y +=+【例5】如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________【例6】给出三个多项式:21212x x +-,21412x x ++,2122x x -.请选择你最喜欢的两个多项式进行加法运算,并把结果因式分解.【当堂检测】1.分解因式:39a a -= , _____________223=---x x x2.对于任意两个实数对(a ,b )和(c ,d ),规定:当且仅当a =c 且b =d 时,(a ,b )=(c ,d ).定义运算“⊗”:(a ,b )⊗(c ,d )=(ac -bd ,ad +bc ).若(1,2)⊗(p ,q )=(5,0),则p = ,q = . 3. 已知a=1.6⨯109,b=4⨯103,则a 2÷2b=( )A. 2⨯107B. 4⨯1014C.3.2⨯105D. 3.2⨯1014 .4.先化简,再求值:22()()(2)3a b a b a b a ++-+-,其中2332a b =-=,.5 先化简,再求值:22()()()2a b a b a b a +-++-,其中133a b ==-,.第7题【课后作业】 一、选择题1.下列运算正确的是( )A.a 2·a=3aB.a 6÷a 2=a 4C.a+a=a 2D.(a 2)3=a 5 2.计算:()23ab=( )A .22a b B .23a b C .26a b D .6ab 3.下列计算正确的是( )A .623a a a ÷= B .()122--=C .()236326x x x -=-· D .()0π31-=4.下列因式分解错误的是( )A .22()()x y x y x y -=+-B .2269(3)x x x ++=+C .2()x xy x x y +=+D .222()x y x y +=+5.若的值为则2y-x 2,54,32==yxA.53 B. -2 C. 553 D. 56 6.下列命题是假.命题的是( ) A. 若x y <,则x +2008<y +2008 B. 单项式2347x y -的系数是-4C. 若21(3)0,x y -+-=则1,3x y ==D. 平移不改变图形的形状和大小7.一个正方体的表面展开图如图所示,每一个面上都写有一个整数,并且相对两个面上所写的两个整数之和都相等,那么( )A .a=1,b=5B .a=5,b=1C .a=11,b=5D .a=5,b=118. 在边长为a 的正方形中挖去一个边长为b 的小正方形(a >b )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )A .2222)(b ab a b a ++=+ B .2222)(b ab a b a +-=- C .))((22b a b a b a -+=-aa bab图甲第8题D .222))(2(b ab a b a b a -+=-+二.填空题.9.分解因式:328m m -= .33416m n mn -=3214x x x +-= ____.33222ax y axy ax y +-= _______. =++22363b ab a . 2232ab a b a -+= ___.10.计算:31(2)(1)4a a -⋅- = .11.计算: ⎪⎭⎫⎝⎛-⋅23913x x =________;()=÷523y y ________. 三.解答题: 12.先化简,再求值:(2)(2)(2)a a a a -+--,其中1a =-.。
初高中衔接专题讲义一、数与式的运算(4课时)(可编辑修改word版)

专题一、数与式的运算课时一:乘法公式一、初中知识1.实数运算满足如下运算律:加法交换律,加法结合律,乘法交换律,乘法结合律,乘法对加法的分配律。
2.乘法公式平方差公式: (a +b)(a -b) =a 2-b 2完全平方公式: (a ±b)2=a 2± 2ab +b 2二、目标要求1.理解字母可以表示数,代数式也可以表示数,并掌握数与式的运算。
2.掌握平方差公式和完全平方公式的灵活运用,理解立方和与差公式,两数和与差的立方公式以及三数和的完全平方公式。
三、必要补充根据多项式乘法法则推导出如下乘法公式(1)(x +a)(x +b) =x 2+ (a +b)x +ab(2)(ax +b)(cx +d ) =acx2+ (ad +bc)x +bd(3)立方和公式: (a +b)(a 2-ab +b 2 ) =a3+b3(4)立方差公式: (a -b)(a 2+ab +b 2 ) =a 3-b3(5)两数和的立方公式:(a +b)3=a3+ 3a 2b + 3ab2+b3(6)两数差的立方公式:(a -b)3=a3- 3a 2b + 3ab 2-b3(7)三数和的平方公式:(a +b +c)2=a 2+b 2+c 2+ 2ab + 2bc + 2ac四、典型例题例1、计算:(1)(x + 2)(x - 5) (3)(2x -1)3(2)(2x + 3)(3x - 2) (4)(2a +b -c)2例2:已知x +y = 3 ,xy = 8 ,求下列各式的值(1)x 2y 2;(2)x 2xy y 2;(3)( x y)2;(4)x 3y 3分析:(1)x 2y 2( x y)2 2 xy(2)x 2xy y 2( x y)2 3 xy(3)( x y)2( x y)2 4 xy(4)x 3y 3( x y)( x 2xy y 2 ) ( x y)[( x y)2 3 xy] 例3:已知a +b +c = 4 ab +bc +ac = 4 求a 2+b 2+c 2的值分析: a2+b2+c2= (a +b +c)2- 2(ab +bc +ac) = 8变式:已知:x2- 3x +1= 0 ,求x3+1x3的值。
中考第一轮复习--第一章数与式
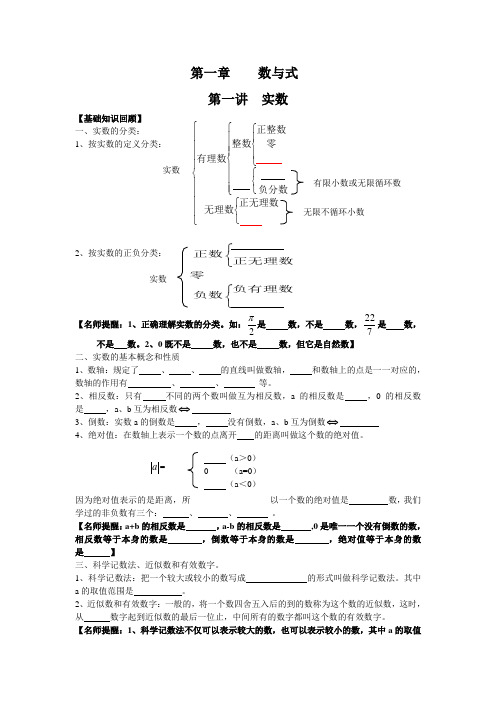
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。
高一数学单元知识点专题讲解1---数与式的运算

【例 8】计算:
(1) ( a + b + 1)(1 − a + b ) − ( a + b )2
(2)
a
a
+
a − ab a + ab
解: 原式 (1) = (1 + b)2 − ( a )2 − (a + 2 ab + b) = −2a − 2 ab + 2 b + 1
【例 7】计算(没有特殊说明,本节中出现的字母均为正数):
3 (1)
2+ 3
11 (2) +
ab
(3) 2
x −
x3 +
8x
2
解: 原式 (1)
=
3(2 − 3)
3(2 − =
3) = 6 − 3 3
(2 + 3)(2 − 3) 22 − 3
原式 a + b a2b + ab2
(2) =
=
ab
ab
3/7
解:( )原式 1
= 43 + m3 = 64 + m3
( )原式 2
= (1 m)3 − (1 n)3 = 1 m3 − 1 n3
5
2 125 8
( )原式 3
= (a 2 − 4)(a 4 + 4a 2 + 42 ) = (a 2 )3 − 43 = a 6 − 64
( )原式 4
= (x + y)2 (x 2 − xy + y 2 )2 = [(x + y)(x 2 − xy + y 2 )]2
三、分式
4/7
第一讲 数与式

初中数学暑假复习讲义第一讲 数与式一、学习指引1.知识要点(1)运算与运用(2)数的规律探究(3)新背景下的数的运算 (4)整式、分式、二次根式(5)代数式的值 2.方法指导(1)巧算要注意算式的特点,运用运算律适当更换次序,使计算简便,平时要不断归纳拆、拼、凑整、交换等运算技巧. (2)数的规律探究主要是解题的过程中去找出内在的规律(3)解决定义新运算的问题,关键是通过新运算的定义,将新运算转化为常规运算.(4)对于代数式的化简、求值,常用到的技巧有:①因式分解,对所给的条件、所求的代数式实施因式分解,达到化繁为简的目的;②运算律,适当运用运算律,也有助于化简; ③换元、配方、待定系数法、倒数法等;④有时对含有根式的等式两边同时实施平方,也不失为一种有效的方法.二、典型例题例1. 计算 (1)99163135115131++++(2)(21+31+……+20021)(1+21+31+……+20011)- (1+21+31+……+20021)(21+31+……+20011)(3)设22211148()34441004A =⨯++---,则与A 最接近的正整数是( ) A.18 B.20 C.24 D.25例2. 将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.例3.(1) 一串数1,1,1,2,2,3,4,5,7,9,12,16,21,……称为帕多瓦数列,请第1个图形第2个图形第3个图形第4个图形…根据这个数列的一个规律,写出其中的第19个数是 .(2)将正整数按如图所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示9,则表示58的有序数对是( ) A.(11,3) B.(3,11) C.(11,9) D.(9,11)例4. 已知123112113114,,,...,1232323438345415a a a =+==+==+=⨯⨯⨯⨯⨯⨯依据上述规律,则99a = .例5.(1)y =︱x +1︱+︱x -2︱+︱x -3︱的最小值 .(2)试求︱x -1︱+︱x -2︱+︱x -3︱+……+︱x -1999︱的最小值.例6.(1)刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当任意实数对(a ,b )进入其中时,会得到一个新的实数:a 2+b -1,例如把(3,-2)放入其中,就会得到32+(-2)-1=6.现将实数对(m ,-2m )放入其中,得到实数2,则m = . (2)在平面直角坐标系中,对于平面内任一点()a b ,,若规定以下三种变换:()()()()1313;f a b a b f -=-如①,=,.,,, ()()()()1331;g a b b a g =如②,=,.,,,()()()()1313h a b a b h --=--如③,=,.,,,. 按照以上变换有:(())()()233232f g f -=-=,,,,那么()()53f h -,等于( )A .()53--,B .()53,C .()53-,D .()53-,(3) 定义一种对正整数n 的“F ”运算:①当n 为奇数时,结果为3n +5;②当n 为偶数时,结果为kn2(其中k 是使k n 2为奇数的正整数),并且运算重复进行.例如,取n=26,则:若n =49,则第449次“F 运算”的结果是_____________.26134411第一次F ② 第二次F ① 第三次F ② …例7.(1)化简:22221369x y x y x y x xy y +--÷--+=_______ ; (2) 若x 2-2y +6x +10+y 2=0,则223442xy y x x yx +--=__________;(3)设512a =,则5432322a a a a a a a+---+=-________. (4)已知b a x -=c b y -=ac z -,那么x+y+z= .例8.(1)如果式子aa ---11)1( 根号外的因式移入根号内,化简的结果为( ) A .a -1 B .1-a C .1--a D .a --1(2) 已知)0,0(02>>=+-y x y xy x ,则yxy x y xy x 4353-++-的值为 ( )A .31 B .21 C .32D .43例9.(1)设N=23x +92y 为完全平方数,且N不超过2392,则满足上述条件的一切正整数对(x ,y )共有多少对?(2)一个一次函数的图象与直线y =45x +495平行,与x 轴、y 轴的交点分别为A、B,并且过点(-1,-25),则在线段AB上(包括点A、B),横、纵坐标都是整数的点有多少个?(3) 如图,菱形ABCD 的对角线长分别为a b 、,以菱形ABCD 各边的中点为顶点作矩形1111A B C D ,然后再以矩形1111A B C D 各边的中点为顶点作菱形2222A B C D ,……,如此下去.则得到四边形2009200920092009A B C D 的面积用含a b 、的代数式表示为__________.4=1+3 9=3+616=6+10…第一讲 实数同步练习活动基地 班级 姓名【基础巩固】一、选择题1. 若的值为则2y-x 2,54,32==yx( )A.53 B.-2 C.553 D.562. 已知a -b=b -c=52,a 2+b 2+c 2=1则ab +bc +ca 的值等于 ( ) A.2513 B.2512 C.53 D.523.古希腊著名的毕达哥拉斯学派把1、3、6、10… 这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻 “三角形数”之和.下列等式中,符 合这一规律的是( ) A .13 = 3+10 B .25 = 9+16 C .36 = 15+21D .49 = 18+314.观察以下数组:(1),(3、5),(7、9、11),(13、15、17、19),…问2009在第( )组.A.44 B. 45 C.46 D.47 5.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式.....,如a b c ++就是完全对称式.下列三个代数式:①2)(b a -;②ab bc ca ++; ③222a b b c c a ++.其中是完全对称式的是( )A .①②B .①③C . ②③D .①②③6.某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k 棵树种植在点)(k k k y x P ,处,其中11=x ,11=y ,当k ≥2时,⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ,[a ]表示非负实数a 的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2009棵树种植点的坐标为A.(5,2009)B.(6,2010)C.(3,401)D.(4,402)7.下面是按一定规律排列的一列数:第1个数:11122-⎛⎫-+ ⎪⎝⎭;第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭; 第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭; ……第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭.那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是 ( )A .第10个数B .第11个数C .第12个数D .第13个数二、填空题8.观察下表,回答问题:第 个图形中“△”的个数是“○”的个数的5倍9.已知Rt △ABC 中,AC=3,BC= 4,过直角顶点C 作CA 1⊥A B ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去,得到了一组线段CA 1,A 1C 1,12C A ,…,则CA 1= ,=5554C A A C .10.已知21(123...)(1)n a n n ==+,,,,记112(1)b a =-,2122(1)(1)b a a =--,…,122(1)(1)...(1)n n b a a a =---,则通过计算推测出n b 的表达式nb =_______.11.已知25350x x --=,则22152525x x x x --=-- . 12. 正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2C 1,C 2,C 3,…分别在直线y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2), 则B n 的坐标是______________.三、解答题13.121+2221+3321+4421+ (101021)序号1 2 3 …图形… y xOC 1B 2A 2 C 3B 1 A 3B 3 A 1C 2(第5题图)14. 若4x -3y -6z=0, x+2y -7z=0 (xyz ≠0),求代数式222222103225z y x z y x ---+的值.【能力拓展】15.如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于E 1,连结1BE 交1CD 于2D ;过2D 作22D E AC ⊥于2E ,连结2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…,如此继续,可以依次得到点45D D ,,…,n D ,分别记112233BD E BD E BD E △,△,△,…,n n BD E △的面积为123S S S ,,,…n S .则n S =________ABC S △(用含n 的代数式表示).16.如图所示,P 1(x 1,y 1)、P 2(x 2,y 2),……P n (x n ,y n )在函数y=x9(x >0)的图象上,△OP 1A 1,△P 2A 1A 2,△P 3A 2A 3……△P n A n -1A n ……都是等腰直角三角形,斜边OA 1,A 1A 2……A n-1A n ,都在x 轴上,则y 1+y 2+…y n = .(第2题)17.对任意实数x 、y ,定义运算x *y 为x *y=ax+by+cxy 其中a 、b 、c 为常数,等式右端运算是通常的实数的加法和乘法.现已知1*2=3,2*3=4,并且有一个非零实数d ,使得对于任意实数x,都有x *d=x ,求d 的值.18.如图所示,在矩形ABCD 中,AB =12,AC =20,两条对角线相交于点O . 以OB 、OC 为邻边作第1个平行四边形OBB 1C ,对角线相交于点A 1;再以A 1B 1、A 1C 为邻边作第2个平行四边形A 1B 1C 1C ,对角线相交于点O 1;再以O 1B 1、O 1C 1为邻边作第3个平行四边形O 1B 1B 2C 1……依次类推. (1)求矩形ABCD 的面积;(2)求第1个平行四边形OBB 1C 、第2个平行四边形A 1B 1C 1C 和第6个平行四边形的面积.OA BCD A 1O 1 BC A E 1 E 2 E 3D 4 D 1 D 2D 3 (第15题)第一讲数与式(典型例题)例1.(1)115(2)20021 提示:设1+21+31+……+20011=a ,21+31+……+20011=b ,则a -b =1 (3) D例2.(1)46 例3.(1)114(2)A 例4.9999100例5.(1)4(2)用几何意义做比较方便,只有x 取1,2,……,1999的中间位置时最小,所以x=1000,原式= 999000 例6.(1)3或-1(2)B (3)98 例7.(1)y x y -2(2)151(3)-2 (4)0 例8.(1)C (2)D 例9.(1)27(2)5(3)(21)3000第一讲 数与式(同步练习)【基础巩固】 一.选择题1.A2.A3.C4.B5.A6.D7.A 二.填空题 7.208.512,45 9.12++n n 10.528 11.(2n -1,2n-1) 三.解答题 12.102410235513.-13 【能力拓展】 14.(11+n )215.3n 16. 17.1*2=a+2b+2c=3 ① 2*3=2a+3b+6c=4 ②x *d=ax+bd+cxd=(a+cd)x+bd=x ③ 由③得 a+cd=1 bd=0 因为d ≠0,所以b=0 代入①得a+2c=3,代入②得2a+6c=4,从而解得a=5,c= -1,将a=5,c= -1代入a+cd=1得d=4 17.(1)192,(2)96,48,3第二讲 方程与方程组一、学习指引1.知识要点(1)一元一次方程 (2)二元一次方程组 (3)一元二次方程 (4)分式方程 (5)方程的整数根 (6)方程应用问题2.方法指导(1)一元一次方程经变形总可以化成ax=b 的形式,此时需注意对字母系数的讨论.(2)二元及多元(二元以上)一次方程组的求解,主要是通过同解变形进行消元,最终转化为一元一次方程来解决.所以,解方程组的基本思想是消元.(3)方程ax 2+bx+c=0(a ≠0)称为一元二次方程:①一元二次方程的基本解法有开平方法、配方法、公式法和因式分解法.②对于方程ax 2+bx+c=0(a ≠0), b 2-4ac 称为该方程的根的判别式. (4)解分式方程的基本方法:①去分母;②求出整式方程未知数的值;③验根.(5)列方程(组)解应用题其具体步骤是: ①审--理解题意,弄清问题中已知量是什么,未知量是什么,问题给出和涉及的相等关系是什么;②设--即找出题中和未知量,选择其中一个设为未知数;③列--找出题中和等量关系,列出方程;④解--解出所列的方程;⑤答--检验作答.其中列是关键,特别是找等量关系。
