无机材料科学基础第九章习题
无机材料科学基础综合测试9
测试九问答与计算1．（5分）Si和Al的原子量非常接近（分别为28.09和26.98），但SiO2及Al2O3的密度相差很大（分别为 2.65 g/cm3及 3.96 g/cm3）试运用晶体结构及鲍林规则说明这一差别。
2．（15分）石墨、云母和高岭石具有相似的结构，请分析它们结构的区别以及由此引起的性质上的差异。
3．（1）（5分）在MgO晶体中，肖特基缺陷的生成能为6 ev，分别计算 25 ℃和 1600℃时热缺陷的浓度。
（2）（5分）如果MgO晶体中，含有百万分之一的Al2O3杂质，则在 1600 ℃时，MgO晶体中是热缺陷占优势还是杂质缺陷占优势？请说明原因。
4．（15分）非化学计量缺陷的浓度与周围气氛的性质、压力大小相关，如果增大周围氧气的分压，非化学计量化合物的密度将发生怎样的变化？为什么？5．（10分）在组成为16Na2O.xB2O3.(84-x)SiO2的熔体中，当x<15 mol％时，增加B2O3的含量使粘度升高；当x> 15mol％时，增加B2O3的含量，反而会使粘度降低，为什么？6．（10分）用Na2CO3和Na2SiO3分别稀释同一粘土泥浆，试比较电解质加入量相同时，两种泥浆的流动性、触变性和坯体致密度的大小。
7．（10分）试说明中各项所代表的意义，并解释同样是间隙扩散机构，为什么在相同的温度下，杂质在介质中的扩散系数比介质本身形成间隙离子的扩散系数大？8．（10分）扩散系数与哪些因素有关？为什么？为什么可以认为浓度梯度大小基本上不影响D值，但浓度梯度大则扩散得快又如何解释？9．（1）（8分）当测量氧化铝－水化物的分解速率时，一个学生发现在等温实验期间，重量损失随时间线性增加到50％左右。
超出50％时重量损失的速率就小于线性规律。
线性等温速率随温度指数地增加，温度从 451℃增加到 493℃时速率增大10倍，试计算反应活化能。
（2）（7分）何谓矿化剂？在固相反应中加入少量矿化剂可促进反应加速进行，解释其原因。
无机材料科学基础课后习题答案9
1．碳酸钙的加热分解：。
试用一般热力学方程求分解反应的及分解温度？答案：1123K提示：查表获得有关热力学数据，计算800-1400K间的，再作图，=0所对应的温度为即为分解温度。
解：由《硅酸盐热力学》查得下列数据H。
298=∑（△H。
生，298）产物-∑（△H。
生，298）反应物=-151.90×103-94.05×103+288.45×103=42.5×103卡/摩尔△G。
298=∑△G。
生，298）产物-∑△G。
生，298）反应物=-1.44.40×103-94.26×103+269.78×103=31.12×103卡/摩尔因为△a=11.67+10.55-24.98=-2.76△b=1.08×10-3+2.16×10-3-5.24×10-3=-2×10-3△c=-1.56×105-2.04×105+6.20×105=2.6×105△H.=△H.298-△a·298-1/2△b（298）2+△c（298）-=42500+2.76×298+1/2×2×10-3×（298）2+2.6×105×（298）-1=44283.76积分常数I=（△G..298-△H.）（298）-+△aln298+1/2△b·298+1/2△c（298）-2=-44.17-15.72-0.298+1.46=-58.73因为当△G。
〉0时，CaCO3不能自发分解，当△G。
〈0时，CaCO3自发分解，所以，△G。
=0的温度为CaCO3开始分解的温度由热力学方程△GT。
=△H。
-△aTlnT-1/2△bT2-1/2△CT-+IT令△G。
T=0 解得方程得T=1123K2．碳酸钙的加热分解：。
无机材料科学基础答案第六,七,九,十章习题答案
6-1 略。
6-2 什么是吉布斯相律？它有什么实际意义？解：相律是吉布斯根据热力学原理得出的相平衡基本定律，又称吉布斯相律，用于描述达到相平衡时系统中自由度数与组分数和相数之间的关系。
一般形式的数学表达式为F＝C－P＋2。
其中F为自由度数，C 为组分数，P为相数，2代表温度和压力两个变量。
应用相率可以很方便地确定平衡体系的自由度数。
6-3 固体硫有两种晶型，即单斜硫、斜方硫，因此，硫系统可能有四个相，如果某人实验得到这四个相平衡共存，试判断这个实验有无问题？解：有问题，根据相律，F=C-P+2=1-P+2=3-P，系统平衡时，F=0 ，则P=3 ，硫系统只能是三相平衡系统。
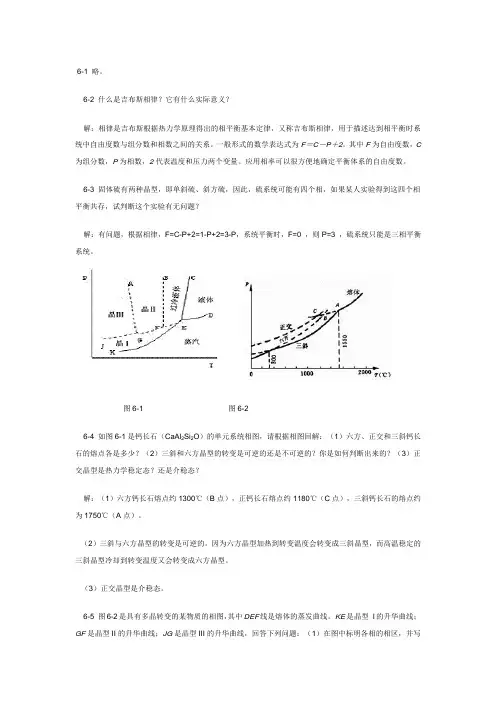
图6-1 图6-26-4 如图6-1是钙长石（CaAl2Si2O）的单元系统相图，请根据相图回解：（1）六方、正交和三斜钙长石的熔点各是多少？（2）三斜和六方晶型的转变是可逆的还是不可逆的？你是如何判断出来的？（3）正交晶型是热力学稳定态？还是介稳态？解：（1）六方钙长石熔点约1300℃（B点），正钙长石熔点约1180℃（C点），三斜钙长石的熔点约为1750℃（A点）。
（2）三斜与六方晶型的转变是可逆的。
因为六方晶型加热到转变温度会转变成三斜晶型，而高温稳定的三斜晶型冷却到转变温度又会转变成六方晶型。
（3）正交晶型是介稳态。
6-5 图6-2是具有多晶转变的某物质的相图，其中DEF线是熔体的蒸发曲线。
KE是晶型I的升华曲线；GF是晶型II的升华曲线；JG是晶型III的升华曲线，回答下列问题：（1）在图中标明各相的相区，并写出图中各无变量点的相平衡关系；（2）系统中哪种晶型为稳定相？哪种晶型为介稳相？（3）各晶型之间的转变是可逆转变还是不可逆转变？解：（1）KEC为晶型Ⅰ的相区，EFBC 过冷液体的介稳区，AGFB晶型Ⅱ的介稳区，JGA晶型Ⅲ的介稳区，CED是液相区，KED是气相区；（2）晶型Ⅰ为稳定相，晶型Ⅱ、Ⅲ为介稳相；因为晶型Ⅱ、Ⅲ的蒸汽压高于晶型Ⅰ的，即它们的自由能较高，有自发转变为自由能较低的晶型Ⅰ的趋势；（3）晶型Ⅰ转变为晶型Ⅱ、Ⅲ是单向的，不可逆的，多晶转变点的温度高于两种晶型的熔点；晶型Ⅱ、Ⅲ之间的转变是可逆的，双向的，多晶转变点温度低于Ⅱ、Ⅲ的熔点。
习题和思考题
《无机材料科学基础》习题和思考题第一章晶体1.球体按立方最紧密堆积方式堆积，取出立方晶胞，画出立方晶胞中的四面体空隙和八面体空隙的位置分布图。
2.用鲍林规则分析氧化镁晶体结构。
已知镁离子半径为0.65Å，氧离子半径为1.40Å。
（1）确定晶胞中质点的位置坐标；（2）计算每个晶胞中含氧化镁“分子”数，（3）已知晶胞常数a=4.20 Å，求氧化镁堆积系数和密度，（4）氧化镁晶体中最邻近的两个镁离子中心距为多少？次邻近的两个镁离子中心距为多少？最邻近和次邻近的两个氧离子中心距为多少？（5）画出氧化镁晶胞的（111）、（110）、（100）面的质点分布图并在图上标出氧离子的密排方向，求个面的面密度。
3．已知纤锌矿结构中存在两套硫离子和两套锌离子的六方底心格子，并已知锌离子填充在硫离子最紧密堆积体的四面体空隙中，现以一套硫离子的等同点为基准取六方晶胞，画出晶胞中的质点分布图，计算晶胞中所含式量分子数。
4．完成下表5. 六方最紧密堆积与四方最紧密堆积的堆积密度相同，为什么许多氧化物是以氧离子的立方最紧密堆积为基础，而较少以六方最紧密堆积为基础？6. 用鲍林规则分析镁橄榄石的结构：P48 图2-18（1）标记为50的Mg2+与哪几个氧离子配位形成[MgO6]八面体？写出O2+的标高；（2）标记为25的两个O2+与哪几个镁离子配位？写出Mg2+离子的标高；（3）标记为75的O2+离子与哪几个镁离子配位？写出Mg2+离子的标高；（4）标记为0和50的两个Mg2+的[MgO6] 八面体共用几个顶点？写出O2+的标高；（5）[SiO4] 和 [MgO6] 之间、[MgO6]和[MgO6] 八面体之间有那些连接方式？（6）镁橄榄石的晶胞是什么形状？计算晶胞中含有的式量分子数。
第二章晶体缺陷1.氧化镁为氯化钠型结构，氧化锂为反萤石型结构，在两种结构中氧离子都作立方最紧密堆积，为什么在氧化镁中主要的热缺陷是肖特基型，而在氧化锂中却是弗伦克尔型？萤石型结构的氧化物晶体中常见的热缺陷估计主要是什么类型？为什么？2.已知氯化钠晶体中肖特基缺陷形成焓为2.2ev，而氧化镁晶体中肖特基缺陷形成焓为6ev，试分别计算400℃时氯化纳晶体与氧化镁晶体中肖特基缺陷的浓度。
第9章-相变(无机材料科学基础)
第二节 液－固相变
一、液－固相变过程热力学
（一）相变过程中的不平衡状态及亚稳区
➢ 但是实际上，要冷却到比相变温 度更低的某一温度例如C，(气液)和E(液-固)点时才能发生相变， 即凝结出液相或析出固相。
➢ 这种理论上应发生相变而实际上 不能发生相转变的区域(阴影区) 称亚稳区。亚稳区内，旧相能以 亚稳态存在，新相还不能生成。
相变成核位垒：临界半径 rK 时，系统中单位体积自由能变化为：
GK
32 3
n 3
GV2
16
n 3
GV2
1 3
16
n 3
GV2
1 3
AK
其中：AK
4rK2 n
16
n 3
GV2
GK — 成核位垒，相变发生时必须 克服的位垒。
系统内能形成 rK 大小的粒子数 nK ： nk exp Gk
GS LS ALS r 2 SM LM
➢新相晶核与成核基体的接触角为： cos LM MS
➢非均匀成核临界核胚半径： rk*
2 LS
GV
LS
➢非均匀成核时的临界成核位垒：
Gk*
16 3
LS
3G 2
[2 cos 1 cos 2 ]
4
V
Gk* GK f
f 2 cos 1 cos 2
二、液-固相变过程动力学
成核（核化）：晶核形成过程 析晶
长大（晶化）：晶核长大过程
1、均匀成核
成核速率：单位时间内单位体积的液相中生成的晶核数目
成核速率IV=单位体积中临界核胚数 NK×与临界尺寸的核相接触的原子数 Ni×单个原子与临界尺寸的核相撞而附 于其上的频率v
I ni nk
无机及分析化学-第九章答案
无机及分析化学-第九章答案无机及分析化学-第九章答案第九章习题解答1．离子键无饱和性和方向性，而离子晶体中每个离子有确定的配位数，二者有无矛盾？答：二者无矛盾。
离子键无饱和性和方向性是由离子特征决定的。
只要离子晶体里自带有不同的电荷就会有库伦作用，无论周围的空间有多少带有相异电荷的离子，都会产生库伦吸引力，这就决定了离子键的不饱和性，而电荷相异的离子在任意方向的这种作用依然存在。
即没有固定方向，不存在方向性。
而离子在离子晶体由于空间条件及离子本身大小的限制，使一个离子周围只能有确定数目的作用，即配位数一定。
但相邻的离子间库伦引力依然存在，故两者不矛盾。
2．下列双原子分子或离子，哪些可稳定存在？哪些不可能稳定存在？请将能稳定存在的双原子分子或离子按稳定性由大到小的顺序排列起来。
H 2 He 2 He 2+ Be 2 C 2 N 2 N 2+答： H 2σ1s 2 键级=1202=- He 2σ1s 2σ1s *2 键级=0222=-He 2+σ1s 2σ1s *1 键级=5.0212=- Be 2σ1s 2σ1s *2σ2s 2σ2s *2 键级=0244=- C 2σ1s 2σ1s *2σ2s 2σ2s *2π2py 2π2pz 2 键级=2248=- N 2σ1s 2σ1s *2σ2s 2σ2s *2π2py 2π2pz 2σ2px 2 键级=32410=- N 2+ σ1s 2σ1s *2σ2s 2σ2s *2π2py 2π2pz 2σ2px 1键级=5.2249=- 稳定存在的分子或离子：H 2 He 2+ C 2 N 2 N 2+ 不能稳定存在的分子或离子：He 2 Be 2稳定性次序：N 2>N 2+>C 2>H 2>He 2+3．第二周期某元素的单质是双原子分子，键级为1是顺磁性物质。
(1)推断出它的原子序号； (2)写出分子轨道中的排布情况；答：(1)原子序号5(2)B 2 σ1s 2σ1s *2σ2s 2σ2s *2π2py 1π2pz 14．在BCl 3和NCl 3分子中，中心原子的氧化数和配体数都相同，为什么二者的中心原子采取的杂化类型、分子构型却不同？答：BCl 3与NCl 3分子中，中心原子不同，中心原子的电子结构不同，使得两者的中心原子采用不同的杂化方式：B采用的是sp2杂化，每个杂化轨道的的夹角是120o，与Cl原子以3p x轨道形成3个σ键，分子呈平面三角形。
无机材料科学基础课后习题
晶体结构2、（1）一晶面在x、y、z轴上的截距分别为2a、3b、6c，求出该晶面的米勒指数；（2）一晶面在x、y、z轴上的截距分别为a/3、b/2、c，求出该晶面的米勒指数。
解：（1）h:k:l=1/2:1/3:1/6=3:2:1,∴该晶面的米勒指数为（321）；（2）（321）5、已知Mg2+半径为0.072nm，O2-半径为0.140nm，计算MgO晶体结构的堆积系数与密度。
解：MgO为NaCl型，O2-做密堆积，Mg2+填充空隙。
rO2- =0.140nm，rMg2+=0.072nm，z=4，晶胞中质点体积：(4/3×πr O2-3+4/3×πrMg2+ 3)×4，a=2(r++r-)，晶胞体积=a3，堆积系数=晶胞中MgO体积/晶胞体积=68.5%，密度=晶胞中MgO质量/晶胞体积=3.49g/cm3。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
解：体心：原子数2，配位数8，堆积密度55.5%；面心：原子数4，配位数6，堆积密度74.04%；六方：原子数6，配位数6，堆积密度74.04%。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃，NaC1为80l℃, 请说明这种差别的原因。
解：u=z1z2e2N0A/r0×(1-1/n)/4πε0，e=1.602×10-19，ε0=8.854×10-12，N0=6.×1023，NaCl：z1=1，z2=1，A=1.748，n Na+=7，n Cl-=9，n=8，r0=2.81910-10m，u NaCl=752KJ/mol；MgO：z1=2，z2=2，A=1.748，n O2-=7，n Mg2+=，n=7，r0=2.1010m，u MgO=392KJ/mol；∵u MgO> u NaCl，∴MgO的熔点高。
9、证明等径圆球面心立方最密堆积的空隙率为25．9％；解：设球半径为a，则球的体积为4/3πa3，求的z=4，则球的总体积（晶胞）4×4/3πa3，立方体晶胞体积：(2a)3=16a3，空间利用率=球所占体积/空间体积=74.1%，空隙率=1-74.1%=25.9%。
无机材料科学基础课后习题答案
名师整理优秀资源4.1 名词解释（a）弗伦克尔缺陷与肖特基缺陷；（b）刃型位错和螺型位错解：（a）当晶体热振动时，一些能量足够大的原子离开平衡位置而挤到晶格点的间隙中，形成间隙原子，而原来位置上形成空位，这种缺陷称为弗伦克尔缺陷。
如果正常格点上原子，热起伏后获得能量离开平衡位置，跃迁到晶体的表面，在原正常格点上留下空位，这种缺陷称为肖特基缺陷。
（b）滑移方向与位错线垂直的位错称为刃型位错。
位错线与滑移方向相互平行的位错称为螺型位错。
4.2试述晶体结构中点缺陷的类型。
以通用的表示法写出晶体中各种点缺陷的表示符号。
试举例写出CaCl2中Ca2+置换KCl中K+或进入到KCl间隙中去的两种点缺陷反应表示式。
解：晶体结构中的点缺陷类型共分：间隙原子、空位和杂质原子等三种。
在MX晶体中，间隙原子的表示符号为MI或XI；空位缺陷的表示符号为：VM或VX。
如果进入MX晶体的杂质原子是A，则其表示符号可写成：AM或AX（取代式）以及Ai（间隙式）。
当CaCl2中Ca2+置换KCl中K+而出现点缺陷，其缺陷反应式如下：++2Cl CaCl Cl2CaCl2中Ca2+进入到KCl间隙中而形成点缺陷的反应式为：+2CaCl+2Cl Cl24.3在缺陷反应方程式中，所谓位置平衡、电中性、质量平衡是指什么？解：位置平衡是指在化合物MaXb中，M格点数与X格点数保持正确。
电中性是指在方程式两边应具有相同的b：X=a：M的比例关系，即．名师整理优秀资源有效电荷。
质量平衡是指方程式两边应保持物质质量的守恒。
4.4（a）在MgO晶体中，肖特基缺陷的生成能为6ev，计算在25℃和1600℃时热缺陷的浓度。
（b）如果MgO晶体中，含有百万分之一mol的Al2O3杂质，则在1600℃时，MgO晶体中是热缺陷占优势还是杂质缺陷占优势？说明原因。
解：（a）根据热缺陷浓度公式：（－）exp由题意△G=6ev=6×1.602×10-19=9.612×10-19JK=1.38×10-23 J/KT1=25+273=298K T2=1600+273=1873K-5110=1.92：×exp 298K-9×10=8exp1873K：（b）在MgO中加入百万分之一的Al2O3杂质，缺陷反应方程为：[ ]杂质。
无机非金属材料科学基础习题
第一章【习题】名词解释：等同点、结点、空间点阵、晶体、对称、对称型、晶系、晶类、布拉菲格子、晶胞、晶胞参数、晶体定向、晶面指数、晶向指数、晶带轴定律? 略述从一个晶体结构中抽取点阵的意义和方法？空间点阵与晶体结构有何对应关系？什么叫对称性？晶体的对称性有何特点，为什么？晶体中有哪些对称要素，用国际符号表示。
试找出正四面体、正八面体和立方体中的所有对称元素，并确定其所属点群、晶系。
根据什么将14种布拉维点阵分成七个晶系？各晶系特点如何？为什么14种布拉维点阵中有正交底心而无四方底心和立方底心点阵型式？以图说明。
说明七个晶系的对称特点及晶体几何常数的关系。
什么叫单位平行六面体（或单位）？在三维点阵中选取单位平行六面体应遵循哪些原则？为什么？a≠b≠c, α=β=γ=90℃的晶体属于什么晶系？a≠b≠c, α≠β≠γ≠90°的晶体属什么晶系？能否据此确定这二种晶体的布拉维点阵？一个四方晶系晶体的晶面，其上的截距分别为3a、4 a，6c，求该晶面的晶面指数。
四方晶系晶体a＝b，c＝1/2a。
一晶面在X、Y、Z轴上的截距分别为2a, 3b和6c。
给出该晶面的密勒指数。
某一晶面在x、y、z三个坐标轴上的截距分别为1a，∞b,3c，求该晶面符号。
在正交简单点阵、底心点阵、体心点阵、面心点阵中分别标出（110）、（011）、（101）三组晶面，并指出每个晶面上的结点数。
在立方晶系中画出下列晶面：a）（001）；b）（110）；c）（111）。
在所画的晶面上分别标明下列晶向：a）[210]；b）[111]；c）[101]。
试说明在等轴晶系中，（111）、（111）、（222）、（110）与（111）面之间的几何关系。
在立方晶系晶胞中画出下列晶面指数和晶向指数：（001）与[210]，(111)与[112]，(110)与[111]，（322）与[236]，(257)与[111]，(123)与[121]，(102)，(112)，(213)，[110]，[111]，[120]，[ 321]。
无机材料科学基础试卷
无机材料科学基础试卷第一篇：无机材料科学基础试卷一、名词解释（20分）：1.不一致熔融化合物，连线规则答：不一致熔化合物是一种不稳定的化合物，加热到一定温度会发生分解，分解产物是一种液相和一种固相，液相和固相的组成与化合物组成都不相同。
（2.5分）连线规则：将一界线（或其延长线）与相应的连线（或其延长线）相交，其交点是该界线上的温度最高点。
（2.5分）2.非本征扩散，稳定扩散非本征扩散：受固溶引入的杂质离子的电价和浓度等外界因素所控制的扩散。
或由不等价杂质离子取代造成晶格空位，由此而引起的质点迁移。
（2.5）稳定扩散：若扩散物质在扩散层dx内各处的浓度不随时间而变化，即dc/dt=0。
这种扩散称稳定扩散。
（2.5分）3.非均匀成核, 一级相变非均匀成核：是指借助于表面、界面、微粒裂纹器壁以及各种催化位置等而形成晶核的过程一级相变：体系由一相变为另一相时，如两相的化学势相等但化学势的一级偏微商(一级导数)不相等的称为一级相变。
（2.5）4.晶粒生长，二次再结晶晶粒生长：平衡晶粒尺寸在不改变其分布的情况下，连续增大的过程。
（2.5分）二次再结晶：是少数巨大晶粒在细晶消耗时成核长大的过程。
（2.5分）5.一致熔融化合物，三角形规则答：一致熔融化合物是一种稳定的化合物，与正常的纯物质一样具有固定的熔点，熔化时，产生的液相与化合物组成相同。
（2.5分）三角形规则：原始熔体组成点所在副三角形的三个顶点表示的物质即为其结晶产物；与这三个物质相应的初初晶区所包围的三元无变量点是其结晶结束点。
（2.5分）6.晶粒生长，二次再结晶晶粒生长：平衡晶粒尺寸在不改变其分布的情况下，连续增大的过程。
（2.5分）二次再结晶：是少数巨大晶粒在细晶消耗时成核长大的过程。
（2.5分）7.液相独立析晶，切线规则答：液相独立析晶：是在转熔过程中发生的，由于冷却速度较快，被回收的晶相有可能会被新析出的固相包裹起来，使转熔过程不能继续进行，从而使液相进行另一个单独的析晶过程，就是液相独立析晶。
第9章习题及答案_无机材料科学基础
第九章相变过程9-1 名词解释：一级相变二级相变扩散型相变无扩散型相变扩散控制的长大界面控制的长大9-2 什么叫相变？按照相变机理来划分，可分为哪些相变?9-3 分析发生固态相变时组分及过冷度变化相变驱动力的影响。
9-4 马氏体相变具有什么特征？它和成核－生成相变有何差别?9-5 试分析应变能及表面能对固态相变热力学、动力学及新相形状的影响。
9-6 请分析温度对相变热力学及动力学的影响。
9-7 调幅分解与脱溶分解有何异同点？调幅分解所得到的显微结构与性能有何特点？9-8 当一种纯液体过冷到平衡凝固温度（T0）以下时，固相与液相间的自由焓差越来越负。
试证明在温度T0附近随温度变化的关系近似地为：，式中∆H V <0为凝固潜热。
9-9 在纯液体平衡凝固温度T0以下，临界相变势垒随温度下降而减小，于是有一个使热起伏活化因子exp为极大值的温度。
试证明当T＝T0/3时，exp有极大植。
（提示：利用表达式）9-10 为什么在成核一生长机理相变中，要有一点过冷或过热才能发生相变?什么情况下需过冷，什么情况下需过热？9-11 何谓均匀成核？何谓不均匀成核？晶核剂对熔体结晶过程的临界晶核半径r*有何影响?9-12 在不均匀成核的情况下，相变活化能与表面张力有关，试讨论不均匀成核的活化能△G h*与接触角θ的关系，并证明当时，△G h*是均匀成核活化能的一半。
9-13 铁的原子量为55.84，密度为7.3g/cm3，熔点为1593℃，熔化热为11495J/mol，固－液界面能为2.04×10－5J/cm2，试求在过冷度为10℃、100℃时的临界晶核大小，并估计这些晶核分别由多少个晶胞所组成（已知铁为体心立方晶格，晶格常数a＝0.305nm）。
9-14 熔体冷却结晶过程中，在1000℃时，单位体积自由焓变化△G V418J/cm3；在900℃时是2090J/cm3。
设固－液界面能5×10－5J/cm2，求：（1）在900℃和1000℃时的临界晶核半径；（2）在900℃和1000℃时进行相变所需的能量。
《无机材料科学基础》第九章复习题及答案
12.陶瓷的显微结构主要由哪些基本因子构成？
答：陶瓷是由晶体、玻璃体和气孔组成的多晶多相材料，其显 微结构包括晶体的种类和含量，晶粒尺寸和形状，玻璃相的含 量和分布情况，晶粒之间、晶粒与玻璃相之间的界面，气孔的 数量、尺寸、分布等。
13.氧化铝烧结到接近理论密度时，可使可见光几乎透过100％， 用它来装钠蒸气（在超过大气压的压力下）作为路灯。为通过 烧结实现这一点，请你列出研究方案。
2. 烧结的推动力和晶粒生长的推动力。并比较两者的大小？
解：烧结推动力是粉状物料的表面能（γsv）大于多晶烧结体 的晶界能（γgb），即γsv>γgb。 晶粒生长的推动力是晶界两侧物质的自由焓差，使界面向晶 界曲率半径小的晶粒中心推进。烧结的推动力较大，约为 4~20J/g。晶粒生长的推动力较小，约为0.4~2J/g，因而烧结推 动力比晶粒生长推动力约大十倍。
无机材料科学基础
第断题：（正确的打，错误的打）
1. 烧结中始终可以只有一相是固态。
（×）
2. 液相烧结与固相烧结的推动力都是表面能。
（√）
3. 二次再结晶对坯体致密化有利。
（×）
4. 扩散传质中压应力区空位浓度<无应力区空位浓度<张应力
区空位浓度。
（√）
5. 晶粒长大源于小晶体的相互粘结。
答：制备透明氧化铝陶瓷的主要技术措施是：（1）采用高纯 氧化铝原料，Al2O3>99.9%，无杂质和玻璃相；（2）添加 0.1～0.5%MgO，在晶粒表面生成镁铝尖晶石，降低晶界移动 速度，抑制晶粒生长；（3）在氢气或真空中烧结，促进气孔 扩散；（4）采用热压烧结，提高制品致密度。
6.试说明晶界能总是小于相邻二个晶粒表面能之和？
解：在恒温恒压条件下增加单位表面积时体系自由能的增量称 为表面能，而形成单位新界面所需要的能量称为界面能。表面 能和界面能的本质是处在表面或界面上的质点受到不对称力场 作用，与晶体内部质点相比具有较高的能量。晶粒的表面能指 晶粒与气相接触，界面能通常指两个晶粒相接触。显然，晶粒 与气相接触时，表面质点受到力场的不对称性远远大于两个晶 粒相接触时。因此，界面能总是小于相邻二个晶粒表面能之和。
材料科学基础5---9章习题
第5章材料的形变和再结晶1. 有一70MPa应力作用在fcc晶体的[001]方向上，求作用在（111）和（111）滑移系上的分切应力。
答案:矢量数性积a×b=ïaï×ïbï Þ = a×bïaï×ïbï滑移系：（负号不影响切应力大小，故取正号）滑移系：2. Zn单晶在拉伸之前的滑移方向与拉伸轴的夹角为45°，拉伸后滑移方向与拉伸轴的夹角为30°，求拉伸后的延伸率。
答案 :如图所示，AC和A’C’分别为拉伸前后晶体中两相邻滑移面之间的距离。
因为拉伸前后滑移面间距不变，即AC=A’C’故3. 已知平均晶粒直径为1mm和0.0625mm的a-Fe的屈服强度分别为112.7MPa和196MPa,问平均晶粒直径为0.0196mm的纯铁的屈服强度为多少？答案:解得∴4. 铁的回复激活能为88.9 kJ/mol，如果经冷变形的铁在400℃进行回复处理，使其残留加工硬化为60%需160分钟，问在450℃回复处理至同样效果需要多少时间？答案:（分）5. 已知H70黄铜（30%Zn）在400℃的恒温下完成再结晶需要1小时，而在390℃完成再结晶需要2小时，试计算在420℃恒温下完成再结晶需要多少时间？答案：再结晶是一热激活过程，故再结晶速率：，而再结晶速率和产生某一体积分数所需时间t成反比，即∝∴在两个不同的恒定温度产生同样程度的再结晶时，两边取对数；同样故得。
代入相应数据，得到t3 = 0.26 h。
1．有一根长为5 m，直径为3mm的铝线，已知铝的弹性模量为70GPa，求在200N的拉力作用下，此线的总长度。
答案2．一Mg合金的屈服强度为180MPa，E为45GPa，a）求不至于使一块10mm⨯2mm的Mg板发生塑性变形的最大载荷；b）在此载荷作用下，该镁板每mm的伸长量为多少？答案3. 已知烧结Al2O3的孔隙度为5%，其E=370GPa。
《材料科学基础》习题及参考答案
形核功，还是可以成核的。
答案
(7)测定某纯金属铸件结晶时的最大过冷度，其实测
值与用公式ΔT=0.2Tm计算值基本一致。
答案
(8) 某些铸件结晶时，由于冷却较快，均匀形核率N1
提高，非均匀形核率N2也提高，故总的形核率为N=
N1 +N2。
答案
返回
53
(9) 若在过冷液体中，外加10 000颗形核剂，则结晶
❖ ②比较Cu-10% Sn合金铸件和Cu-30%合金铸件的铸造性能 及铸造组织，说明Cu-10% Sn合金铸件中有许多分散砂眼的 原因。
③ω(Sn}分别为2%，11%和15%的青铜合金，哪一种可进行 压力加工?哪种可利用铸造法来制造机件?
答案
返7回8
❖ 9.如下图所示，已知A，B，C三组元固态完全不互溶，质量 分数分别84%A,，10%B，10%C的O合金在冷却过程中将进 行二元共晶反应和三元共晶反应，在二元共晶反应开始时， 该合金液相成分(a点)为60%A，20%B，20%C，而三元共 晶反应开始时的液相成分(E点)为50%A，10%B，40%C。
答案
返回
6
❖ 6.位错受力后运动方向处处垂直于位错线，在运动
过程中是可变的，晶体作相对滑动的方向应是什么
方向？
答案
❖ 7.位错线上的割阶一般如何形成？
答案
❖ 8.界面能最低的界面是什么界面？
答案
❖ 9. “小角度晶界都是由刃型位错排成墙而构成的”这
种说法对吗？
答案
返回
7
三、综合题
❖ 1. 作图表示立方晶体的（123）（0 -1 -2） （421）晶面及[-102][-211][346]晶向。 答案
❖ 9. 在Fe中形成1mol 空位的能量为104. 67kJ，
材料科学基础第九章答案
第九章答案9-2什么叫相变？按照相变机理来划分，可分为哪些相变?解：相变是物质系统不同相之间的相互转变。
按相变机理来分，可以分为扩散型相变和非扩散型相变和半扩散型相变。
依靠原子或离子长距离扩散进行的相变叫扩散型相变。
非扩散型型相变指原子或离子发生移动，但相对位移不超过原子间距。
9-3分析发生固态相变时组分及过冷度变化相变驱动力的影响。
解：相变驱动力是在相变温度下新旧相的体自由能之差（），而且是新相形成的必要条件。
当两个组元混合形成固溶体时，混合后的体系的自由能会发生变化。
可以通过自由能-成分曲线来确定其相变驱动力的大小。
过冷度是相变临界温度与实际转变温度之差，相变形核的热力学条件是要有过冷度。
已知驱动力与过冷度之间的关系是：,这进一步说明了形核的热力学条件。
9-4马氏体相变具有什么特征？它和成核－生成相变有何差别?解：马氏体相变是替换原子经无扩散切变位移(均匀或不均匀)并由此产生形状改变和表面浮凸、曾不变平面应变特征的一级形核、长大的相变。
特征：具有剪切均匀整齐性、不发生原子扩散、相变速度快、相变有一定范围、有很大的切变型弹性应变能。
成核－生长过程中存在扩散相变，母相与晶相组成可相同可不同，转变速度较慢，无明显的开始和终了温度。
9-5试分析应变能及表面能对固态相变热力学、动力学及新相形状的影响。
解：物质的表面具有表面张力σ,在恒温恒压下可逆地增大表面积dA,则需功σdA,因为所需的功等于物系自由能的增加,且这一增加是由于物系的表面积增大所致,故称为表面自由能或表面能。
应变能和表面能可以影响相变驱动力的大小，和新相的形状。
9-6请分析温度对相变热力学及动力学的影响。
解：当温度降低，过冷度增大，成核势垒下降，成核速率增大，直至达到最大值；当温度继续下降，液相粘度增加，原子或分子扩散速率下降。
温度过高或过低对成核和生长速率均不利，只有在一定的温度下才有最大成核和生长速率。
9-7调幅分解与脱溶分解有何异同点？调幅分解所得到的显微结构与性能有何特点？解：调幅分解通过扩散偏聚由一种固溶体分解成与母相结构相同而成分不同的两种固溶体。
材料科学基础课程习题
材料科学基础课程习题第⼀章原⼦排列与晶体结构1. fcc 结构的密排⽅向是，密排⾯是，密排⾯的堆垛顺序是，致密度为，配位数是 ,晶胞中原⼦数为，把原⼦视为刚性球时，原⼦的半径r 与点阵常数a 的关系是；bcc 结构的密排⽅向是，密排⾯是 ,致密度为 ,配位数是 ,晶胞中原⼦数为，原⼦的半径r 与点阵常数a 的关系是；hcp 结构的密排⽅向是，密排⾯是，密排⾯的堆垛顺序是，致密度为，配位数是 ,，晶胞中原⼦数为，原⼦的半径r 与点阵常数a 的关系是。
2. Al 的点阵常数为0.4049nm ，其结构原⼦体积是，每个晶胞中⼋⾯体间隙数为，四⾯体间隙数为。
3. 纯铁冷却时在912ε发⽣同素异晶转变是从结构转变为结构，配位数，致密度降低，晶体体积，原⼦半径发⽣。
4. 在⾯⼼⽴⽅晶胞中画出晶⾯和晶向，指出﹤110﹥中位于（111）平⾯上的⽅向。
在hcp 晶胞的（0001）⾯上标出晶⾯和晶向。
5. 求和两晶向所决定的晶⾯。
6 在铅的（100）平⾯上，1mm 2有多少原⼦？已知铅为fcc ⾯⼼⽴⽅结构，其原⼦半径R=0.175×10-6mm 。
第⼆章合⾦相结构⼀、填空1）随着溶质浓度的增⼤，单相固溶体合⾦的强度，塑性，导电性，形成间隙固溶体时，固溶体的点阵常数。
2）影响置换固溶体溶解度⼤⼩的主要因素是（1）；（2）；（3）；（4）和环境因素。
3）置换式固溶体的不均匀性主要表现为和。
4）按照溶质原⼦进⼊溶剂点阵的位置区分，固溶体可分为和。
5）⽆序固溶体转变为有序固溶体时，合⾦性能变化的⼀般规律是强度和硬度，塑性，导电性。
6）间隙固溶体是，间隙化合物是。
⼆、问答1、分析氢，氮，碳，硼在α-Fe 和γ-Fe 中形成固溶体的类型，进⼊点阵中的位置和固溶度⼤⼩。
已知元素的原⼦半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，α-Fe ：0.124nm ，γ-Fe ：0.126nm 。
第9章习题及答案_无机材料科学基础
第九章相变过程9-1 名词解释：一级相变二级相变扩散型相变无扩散型相变扩散控制的长大界面控制的长大9-2 什么叫相变？按照相变机理来划分，可分为哪些相变?9-3 分析发生固态相变时组分及过冷度变化相变驱动力的影响。
9-4 马氏体相变具有什么特征？它和成核－生成相变有何差别?9-5 试分析应变能及表面能对固态相变热力学、动力学及新相形状的影响。
9-6 请分析温度对相变热力学及动力学的影响。
9-7 调幅分解与脱溶分解有何异同点？调幅分解所得到的显微结构与性能有何特点？9-8 当一种纯液体过冷到平衡凝固温度（T0）以下时，固相与液相间的自由焓差越来越负。
试证明在温度T0附近随温度变化的关系近似地为：，式中∆H V <0为凝固潜热。
9-9 在纯液体平衡凝固温度T0以下，临界相变势垒随温度下降而减小，于是有一个使热起伏活化因子exp为极大值的温度。
试证明当T＝T0/3时，exp有极大植。
（提示：利用表达式）9-10 为什么在成核一生长机理相变中，要有一点过冷或过热才能发生相变?什么情况下需过冷，什么情况下需过热？9-11 何谓均匀成核？何谓不均匀成核？晶核剂对熔体结晶过程的临界晶核半径r*有何影响?9-12 在不均匀成核的情况下，相变活化能与表面张力有关，试讨论不均匀成核的活化能△G h*与接触角θ的关系，并证明当时，△G h*是均匀成核活化能的一半。
9-13 铁的原子量为55.84，密度为7.3g/cm3，熔点为1593℃，熔化热为11495J/mol，固－液界面能为2.04×10－5J/cm2，试求在过冷度为10℃、100℃时的临界晶核大小，并估计这些晶核分别由多少个晶胞所组成（已知铁为体心立方晶格，晶格常数a＝0.305nm）。
9-14 熔体冷却结晶过程中，在1000℃时，单位体积自由焓变化△G V418J/cm3；在900℃时是2090J/cm3。
设固－液界面能5×10－5J/cm2，求：（1）在900℃和1000℃时的临界晶核半径；（2）在900℃和1000℃时进行相变所需的能量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第九章习题与答案
一、判断正误
1、烧结中始终可以只有一相是固态。
（对）
2、液相烧结与固相烧结的推动力都是表面能。
（对）
3、二次再结晶对坯体致密化有利。
（错）
4、扩散传质中压应力区空位浓度<无应力区空位浓度<张应力区空位浓度。
（对）
5、晶粒长大源于小晶体的相互粘结。
（错）
6、一般来说，晶界是气孔通向烧结体外的主要扩散通道。
一般来说，晶界是杂质的富集之
地。
（对）
二、填空
1、烧结的主要传质方式有：蒸发-凝聚传质、扩散传质、流动传质和溶解-沉淀传质四种，这四种传质过程的坯体线收缩ΔL/L与烧结时间的关系依次为ΔL/L=0、ΔL/L～t2/5、ΔL/L～t和ΔL/L～t1/3。
三、选择
1、在烧结过程中，只改变气孔形状不引起坯体收缩的传质方式是（a、c）。
a．表面扩散 b．流动传质 c．蒸发-凝聚 d．晶界扩散
2、在烧结过程中只改变坯体中气孔的形状而不引起坯体致密化的传质方式是（b）。
a. 流动传质
b. 蒸发—凝聚传质
c. 溶解—沉淀
d. 扩散传质
四、问答题
1、典型的传质过程有哪些？各采用什么烧结模型？分析产生的原因是什么？
答：典型的传质过程有：固相烧结的蒸发-凝聚传质、扩散传质，液相烧结的流动传质、溶解-沉淀传质。
固相烧结的蒸发-凝聚传质过程采用中心距不变的双球模型。
固相烧结的扩散传质、液相烧结的流动传质、溶解-沉淀传质过程采用中心距缩短的双球模型。
原因：蒸发—冷凝：压力差ΔP；扩散传质：空位浓度差ΔC；流动传质：应力—应变；
溶解—沉淀：溶解度ΔC（大、小晶粒溶解度不同；自由表面与点接触溶解度）。
2、试述烧结的推动力和晶粒生长的推动力。
并比较两者的大小。
答：烧结推动力是粉状物料的表面能（γsv）大于多晶烧结体的晶界能（γgb），即γsv>γgb。
晶粒生长的推动力是晶界两侧物质的自由焓差，使界面向晶界曲率半径小的晶粒中心推进。
烧结的推动力较大，约为4~20J/g。
晶粒生长的推动力较小，约为0.4~2J/g，因而烧结推动力比晶粒生长推动力约大十倍。
3、在制造透明Al2O3材料时，原始粉料粒度为2μm，烧结至最高温度保温0.5h，测得晶粒尺寸为10μm，试问保温2h，晶粒尺寸多大？为抑制晶粒生长加入0.1％MgO，此时若保温2h，晶粒尺寸又有多大？
解：1、G 2-G02 = kt
= 2 μm, G = 10 μm, t = 0.5 h，得
代入数据：G
k = (102-22)/0.5 (μm2/h)
=192 (μm2/h)
则，保温2h后，晶粒尺寸应为：
2 =192⨯2+22 = 388
G 2 = kt + G
G = 19.7 μm
3 2、加入0.1% MgO，防止二次再结晶，抑制晶界迁移，则应用晶粒生长公式：G 3-G
= kt
将已知数据代入公式求得 k ：
3 )/t =(103-23)/0.5 = 198
4 (μm3/h)
k = (G 3-G
此时保温2h后，晶粒尺寸应为：
3 = 198
4 ⨯2 + 23 = 3976
G 3 = k t + G
G = 15.8 μm
4、在烧结期间，晶粒长大能促进胚体致密化吗？晶粒长大能够影响烧结速率吗？试说明之。
答：晶粒生长是界面移动的结果，并不是原子定向向颈部迁移的传质过程，因而不能促进胚体致密化。
晶界移动可以引起原子跃迁，也可使气孔移入晶粒内，从而影响烧结速率。
因而晶界移动速率需进行控制。
5、说明影响烧结的因素？
答：1、粉末的粒度。
细颗粒增加了烧结推动力，缩短原子扩散距离，提高颗粒在液相中的溶解度，从而导致烧结过程的加速。
2、外加剂的作用。
在固相烧结中，有少量外加剂可与主晶相形成固溶体，促进缺陷增加，在液相烧结中，外加剂改变液相的性质（如粘度，组成等），促进烧结。
3、烧结温度：晶体中晶格能越大，离子结合也越牢固，离子扩散也越困难，烧结温度越高。
4、保温时间：高温段以体积扩散为主，以短时间为好，低温段为表面扩散为主，低温时间越长，不仅不引起致密化，反而会因表面扩散，改变了气孔的形状而给制品性能带来损害，要尽可能快地从低温升到高温，以创造体积扩散条件。
5、气氛的影响：氧化，还原，中性。
6 、成形压力影响：一般说成型压力越大颗粒间接触越紧密，对烧结越有利。
6、试说明晶界能总是小于相邻二个晶粒表面能之和。
答：在恒温恒压条件下增加单位表面积时体系自由能的增量称为表面能，而形成单位新界面所需要的能量称为界面能。
表面能和界面能的本质是处在表面或界面上的质点受到不对称力场作用，与晶体内部质点相比具有较高的能量。
晶粒的表面能指晶粒与气相接触，界面能通常指两个晶粒相接触。
显然，晶粒与气相接触时，表面质点受到力场的不对称性远远大于两个晶粒相接触时。
因此，界面能总是小于相邻二个晶粒表面能之和。
7、在扩散传质的烧结过程中，使坯体致密的推动力是什么？哪些方法可促进烧结？说明原因。
答：在扩散传质的烧结过程中，系统内不同部位（颈部、颗粒接触点、颗粒内部）空位浓度不同，导致原子或质点由颗粒接触点向颈部迁移，填充到气孔中。
因此使坯体致密化的推动力是空位浓度差。
对于扩散传质：（1）控制原料的起始粒度非常重要，颗粒细小的原料可促进烧结，因为颈部增长速率x/r与原料起始粒度r的3/5次方成反比；（2）温度对烧结过程有决定性作用，扩散系数与温度呈指数关系，因此提高温度可加速烧结。
8、晶界遇到夹杂物时会出现几种情况，从实现致密化目的考虑，晶界应如何移动？怎样控制？
答：烧结初期，晶界上气孔数目很多，此时气孔阻止晶界移动，Vb=0。
烧结中、后期，温度控制适当，气孔逐渐减少。
可以出现Vb=Vp，此时晶界带动气孔以正常速度移动，使气孔保持在晶界上，气孔可以利用晶界作为空位传递的快速通道而迅速汇集或消失。
继续升温导致Vb》Vp，晶界越过气孔而向曲率中心移动，气孔包入晶体内部，只能通过体积扩散排除，这是十分困难的。
从实现致密化目的考虑，晶界应带动气孔以正常速度移动，使气孔保持在晶界上，气孔可以利用晶界作为空位传递的快速通道而迅速汇集或消失。
控制方法：控制温度，加入外加剂等。
9、晶粒生长与二次再结晶的特点，以及造成二次再结晶的原因和二次再结晶的方法。
答：晶粒生长：坯体内晶粒尺寸均匀地生长，服从Dl∝d／f公式；平均尺寸增长，不存在晶核，界面处于平衡状态，界面上无应力；晶粒生长时气孔都维持在晶界上或晶界交汇处。
二次再结晶:是个别晶粒异常生长，不服从上式；二次再结晶的大晶粒的面上有应力存在，晶界数大于10的大晶粒，成为二次再结晶的晶核；二次再结晶时气孔被包裹到晶粒内部。
从工艺控制考虑，造成二次再结晶的原因主要是原始粒度不均匀、烧结温度偏高。
防止二次再结晶的最好方法是引入适当的添加剂，它能抑制晶界迁移，有效地加速气孔的排除；控制烧结温度；选择原始粒度的均匀原材料。
10、影响陶瓷烧结的主要因素有哪些？
答：（1）原始粉料的粒度；（2）外加剂的作用；（3）烧结温度与保温时间；（4）盐类的选择及煅烧条件；（5）气氛的影响；（6）成型压力。
11、陶瓷的显微结构主要由哪些基本因子构成？
答：陶瓷是由晶体、玻璃体和气孔组成的多晶多相材料。
其显微结构包括晶体的种类和含量，晶粒尺寸和形状，玻璃相的含量和分布情况，晶粒之间、晶粒与玻璃相之间的界面，气孔的数量、尺寸、分布等。
12、氧化铝烧结到接近理论密度时，可使可见光几乎透过100％，用它来装钠蒸气（在超过大气压的压力下）作为路灯。
为通过烧结实现这一点，请你列出研究方案。
答：制备透明氧化铝陶瓷的主要技术措施是：（1）采用高纯氧化铝原料，Al2O3>99.9%，无杂质和玻璃相；（2）添加0.1～0.5%MgO，在晶粒表面生成镁铝尖晶石，降低晶界移动速度，抑制晶粒生长；（3）在氢气或真空中烧结，促进气孔扩散；（4）采用热压烧结，提高制品致密度。