恒定磁场的旋安培环路定律
合集下载
磁场3(安培环路定理、洛仑兹力)
8-4 稳恒磁场的安培环路定理
一、安培环路定理 静电场的环路定理 磁场的环路定理 1.推导
LE dl 0 B dl ?
L
以无限长直导线为例
推广
1). 圆形环路
B dl LB dl cos 0 B Ldl
L
I
l
r
B
0 I 2 r 0 I B 2 r 2 r
cd
0 NI
B (2r )
0 NI
匝数
0 NI B 2 r
I
I
场点距中心 的距离
3. 均匀通电直长圆柱体的磁场 已知: 无限长载流圆柱体,半径 R 电流强度为 I,电流均匀分布 空间任一点 P ,如图 求:该点的磁感应强度? -------磁场分布
I
R
μ0μ
解: 1. 内部磁场 • 对称性分析 • 做对称性环路
3. B 是全空间电流的贡献,
但只有I内 对环流
B d l 有贡献。
L
4.说明磁场为非保守场称为涡旋场
三、环路定律的应用（重点） B dl 0 I i内
一般步骤: 1.对称性分析 2.做对称性环路
L i
3.用环路定理解题
B dl 0 Ii内
B
二. 应用-------霍耳效应 1879年霍耳（A.H.Hall） 1.定义: 在匀强磁场 B 中，金属导体板通有电流 I B，在与 I 和 B 都垂直上下表面出现横向电势差的现象 实验指出：
பைடு நூலகம்
B
b
IB UH b IB U H RH b
a
++++++++
一、安培环路定理 静电场的环路定理 磁场的环路定理 1.推导
LE dl 0 B dl ?
L
以无限长直导线为例
推广
1). 圆形环路
B dl LB dl cos 0 B Ldl
L
I
l
r
B
0 I 2 r 0 I B 2 r 2 r
cd
0 NI
B (2r )
0 NI
匝数
0 NI B 2 r
I
I
场点距中心 的距离
3. 均匀通电直长圆柱体的磁场 已知: 无限长载流圆柱体,半径 R 电流强度为 I,电流均匀分布 空间任一点 P ,如图 求:该点的磁感应强度? -------磁场分布
I
R
μ0μ
解: 1. 内部磁场 • 对称性分析 • 做对称性环路
3. B 是全空间电流的贡献,
但只有I内 对环流
B d l 有贡献。
L
4.说明磁场为非保守场称为涡旋场
三、环路定律的应用（重点） B dl 0 I i内
一般步骤: 1.对称性分析 2.做对称性环路
L i
3.用环路定理解题
B dl 0 Ii内
B
二. 应用-------霍耳效应 1879年霍耳（A.H.Hall） 1.定义: 在匀强磁场 B 中，金属导体板通有电流 I B，在与 I 和 B 都垂直上下表面出现横向电势差的现象 实验指出：
பைடு நூலகம்
B
b
IB UH b IB U H RH b
a
++++++++
磁场的安培环路定理
电荷均匀分布
E
2 0r
E0
E
2 0r
E
r 2 0 R2
E 2 0r
电流均匀分布
B 0I 2r
B0
B 0I 2r
B
0 Ir 2R 2
B 0I 2r
(16)磁场的安培环路定理 （2）面对称
无限大载流导体薄板
I
已知：导线中电流强度 I
单位长度
位置移动
I1 I2
I4
I3
l
不变
? B dl 0 Ii 0 ( I2 I3 )
? 改变
?
不变
(16)磁场的安培环路定理
注意3
安培环路定理
n
B dl 0 Ii
i 1
当电流呈体分布时 B dl 0 S j dS
闭合路径包围的电流为电流
导线匝数n
解：分析对称性
磁力线如图 作积分回路如图
ab、cd与导体板等距
dB
ba
.........
cd
(16)磁场的安培环路定理
计B算 d环l 流abBdl cos 0
c
b
Bdl
cos
2
cd Bdl cos 0
da
Bdl
cos
2
B ab B cd
2B ab
l
B B1 B2 B3
Bdl
l
0 (I 2
I3)
【总结】以上结果对任意 形状的闭合电流（伸向无 限远的电流）均成立.
安培环路定理
11-5真空中磁场的安培环路定理
L
0 I d d L 2 L 0 I 2
1 2
L1
L2
I
o I B 2 r
A
0
B
L2 L1
规定：与L绕向成右旋关系 Ii > 0 与L绕向成左旋关系 Ii < 0 例如：
I2
I1
I3
L
I4
I
L
I I I 1 2 3 i
0 I
2πr
r
B
B 外 方向与I指向满足右旋关系
B内 0
B外
O
R
r
练习：同轴的两筒状导线通有等值反向的电流I,
求 B 的分布。
(1) r R2 , B 0
0 I ( 2) R1 r R2 , B 2r
R2
R1
I
r I
( 3) r R1 , B 0
0 j B
2
0 j x arctg 2π z z 2
0 zj 1
o
x
0 j
2
解二、用安培环路定理
j
z
l
在对称性分析的基础上
x
选如图安培环路 得：B
由：
L
B dl 2lB 0 jl
0 j
2
思考：如果载Байду номын сангаас平面不是无限宽， 思考 能否用叠加原理求解？ 能否用安培环路定理求解？
例4. 求无限长载流圆柱形导体的磁场分布. 对称性分析：
L
dI
r
dI dI o r dI
dB
dB
I
0 I d d L 2 L 0 I 2
1 2
L1
L2
I
o I B 2 r
A
0
B
L2 L1
规定：与L绕向成右旋关系 Ii > 0 与L绕向成左旋关系 Ii < 0 例如：
I2
I1
I3
L
I4
I
L
I I I 1 2 3 i
0 I
2πr
r
B
B 外 方向与I指向满足右旋关系
B内 0
B外
O
R
r
练习：同轴的两筒状导线通有等值反向的电流I,
求 B 的分布。
(1) r R2 , B 0
0 I ( 2) R1 r R2 , B 2r
R2
R1
I
r I
( 3) r R1 , B 0
0 j B
2
0 j x arctg 2π z z 2
0 zj 1
o
x
0 j
2
解二、用安培环路定理
j
z
l
在对称性分析的基础上
x
选如图安培环路 得：B
由：
L
B dl 2lB 0 jl
0 j
2
思考：如果载Байду номын сангаас平面不是无限宽， 思考 能否用叠加原理求解？ 能否用安培环路定理求解？
例4. 求无限长载流圆柱形导体的磁场分布. 对称性分析：
L
dI
r
dI dI o r dI
dB
dB
I
大学物理安培环路定理
10-4 安培环路定理静电场的一个重要特征是电场强度E 沿任意闭合路径的积分等于零，即0d =⋅⎰l E l，那么，磁场中的磁感强度B 沿任意闭合路径的积分⎰⋅ld lB 等于多少呢？可以证明：在真空的稳恒磁场中，磁感强度B 沿任一闭合路径的积分（即B 的环流）的值，等于0μ乘以该闭合路径所包围的各电流的代数和，即∑⎰==⋅ni lI10 d il B μ （10-8）安培环路定理与静电场环路定理的比较 讨论：安培环路定理的证明如图(a)所示，有一通有电流I 的长直载流导线垂直于屏幕平面，且电流流向垂直屏幕平面向内. 在屏幕平面上取两个闭合路径1C 和2C ，其中闭合路径1C 内包围的电流为I ，而在闭合路径2C 内没有电流. 从图（b ）可以看出，由于磁感强度B 的方向总是沿着环绕直导线的圆形回路的切线方向，所以对闭合路径1C 或2C 上任意一线元l d ，磁感强度B 与l d 的点积为ϕαd cos d d Br l B ==⋅l B式中r 为载流导线至线元l d 的距离. 由第10-2节二中例1的式（2），上式可写成ϕμϕμd π2d π2d 00Ir rI==⋅l B （1）对于图（a ）的闭合回路1C ，ϕ将由0增至π2. 于是，磁感强度B 沿闭合路径1C 的环流为这就是真空中磁场的环路定理，也称安培环路定理。
它是电流与磁场之间的基本规律之一。
在式（10-8）中，若电流流向与积分回路呈右螺旋关系，电流取正值；反之则取负值。
⎰⎰===⋅1000π2π2d π2d CIIIμμϕμl B （2）可见，真空中磁感强度B 沿闭合路径的环流等于闭合路径所包围的电流乘以0μ，而与闭合路径的形状无关.然而，对于图（a ）中的闭合路径2C ，将得到不同的结果，当我们从闭合路径2C 上某一点出发，绕行一周后，角ϕ的净增量为零，即⎰=0d ϕ于是，由式（1）可得⎰=⋅20d c l B （3）比较式（2）和式（3）可以看出，它们是有差别的. 这是由于闭合路径1C 包围了电流，而闭合路径2C 却未包围电流. 于是我们可以得到普遍的安培环路定理：沿任意闭合路径的磁感强度B 的环流为⎰∑=⋅20d c I μl B式中∑I 是该闭合路径所包围电流的代数和 人物简介：安培简介安培(Andre Marie Ampere,1775-1855)，法国物理学家，对数学和化学也有贡献，他在电磁理论的建立和发展方面建树颇丰。
10恒定磁场 - 安培环路定律
L
I1 I1
L
I2 I 3 I1
（ ） 0 I1 I 2
问
1） B 是否与回路 L 外电流有关？ 2）若 B d l 0 ，是否回路 L上各处 B 0？ L 是否回路 L 内无电流穿过？
4.4 磁偶极子
1 定义： 磁偶极子是指所围成的
面积趋近于0时的载流回路， 用矢量磁偶极矩表示。
0 M A dV 4π V R 4π
J M M
0
M en S R dS
磁化电流模型
两种磁化电流密度与磁化强度的关系为 ：
K M M en
4.5 磁媒质
总结以上分析可得：
① 媒质中磁偶极子产生的磁场，可以看做是由磁化电流
产生的磁场（见公式4-5-10和4-5-11）。 分布的磁化电流所产生的磁场等效地描述； ② 与自由电流一样，磁化电流也遵从毕奥--沙伐定律产 生恒定磁场；
图 磁偶极子受磁场力而转动
4.5 磁媒质
1 磁化的概念：
无外磁场作用时，介质对外不 显磁性， n mi 0
i 1
图3.2.14 介质的磁化
在外磁场作用下，磁偶极子 发生旋转， n
mi 0
i 1
4.5 磁媒质
2 磁化强度：
磁媒质中单位体积内磁偶极矩的矢量和定义为
磁化强度。
M lim
m
i 1
n
i
V 0
V
（A/m）
矢量磁位：
0 m eR A 2 dV 4 V R
磁偶极子模型
4.5 磁媒质
3 等效磁化电流密度：
磁化后，媒质中形成新的电流，称为磁化电流。形成磁化 电流的电子仍然被束缚在原子或分子周围，所以又称为束缚电
I1 I1
L
I2 I 3 I1
（ ） 0 I1 I 2
问
1） B 是否与回路 L 外电流有关？ 2）若 B d l 0 ，是否回路 L上各处 B 0？ L 是否回路 L 内无电流穿过？
4.4 磁偶极子
1 定义： 磁偶极子是指所围成的
面积趋近于0时的载流回路， 用矢量磁偶极矩表示。
0 M A dV 4π V R 4π
J M M
0
M en S R dS
磁化电流模型
两种磁化电流密度与磁化强度的关系为 ：
K M M en
4.5 磁媒质
总结以上分析可得：
① 媒质中磁偶极子产生的磁场，可以看做是由磁化电流
产生的磁场（见公式4-5-10和4-5-11）。 分布的磁化电流所产生的磁场等效地描述； ② 与自由电流一样，磁化电流也遵从毕奥--沙伐定律产 生恒定磁场；
图 磁偶极子受磁场力而转动
4.5 磁媒质
1 磁化的概念：
无外磁场作用时，介质对外不 显磁性， n mi 0
i 1
图3.2.14 介质的磁化
在外磁场作用下，磁偶极子 发生旋转， n
mi 0
i 1
4.5 磁媒质
2 磁化强度：
磁媒质中单位体积内磁偶极矩的矢量和定义为
磁化强度。
M lim
m
i 1
n
i
V 0
V
（A/m）
矢量磁位：
0 m eR A 2 dV 4 V R
磁偶极子模型
4.5 磁媒质
3 等效磁化电流密度：
磁化后，媒质中形成新的电流，称为磁化电流。形成磁化 电流的电子仍然被束缚在原子或分子周围，所以又称为束缚电
大学物理-磁场 安培环路定律
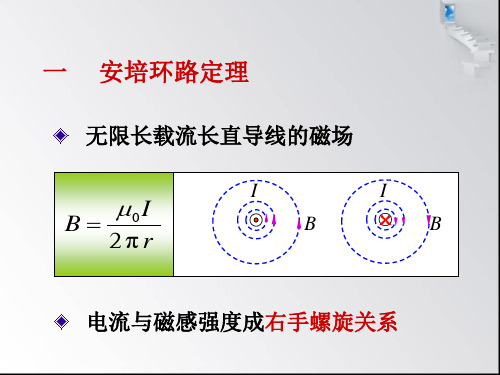
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义：通过任意闭合曲面的磁通
量必等于零（故磁场是无源的）.
B B1 B2 B3
Bdl
l
0(I2 I3)
推广：
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中，磁感强度 B沿任
一闭合路径的积分的值，等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定： I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 （1）对称性分析：环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图，作安培环路
abcda，应用安培环路 定理
b
l B d l 2a B dl
安培环路定律—恒定磁场的旋度方程
磁场是有旋场(涡旋场)，与磁场的散度方程一致
磁感线与电流垂直并相互交链
恒定磁场有旋性的直接证明
B A ( A) 2 A
A 0 Jc (r)dV
4 V
R
0
4
V
J
c
(r
)
1 dV R
0 Jc (r) dV
4 V
R
0 Jc (r) dS 0
4 S R
4 V
R
0
4
V
Jc (r)2
1 R
dV
0 V Jc (r) (r r)dV
R r r
2 1 4 (r r)
r r
冲激函数
0Jc (r )
B 0Jc (r )
Bdl l
S ( B) dS 0
S JC dS 0
Ii
4.3 安培环路定律— 恒定磁场的旋度方程
电工基础教研室 由佳欣
真空中的安培环路定律
Bdl l
0
S JC dS 0Ii来自在真空稳恒磁场中，B 沿任一闭合路径的积分，等于0 乘以
该闭合路径所包围的各电流的代数和
B 对任意闭合曲线L 的环流不恒等于零，磁场是非保守立场，
没有磁势的概念
B 0JC
R r r
1 1 RR
(F) F F (F) F F
恒定电流场是无源场
Jc 0
由于所有电流分布被包含在积分区域内，因此没有电流通过 界面S，面积分为零，则有 A 0
恒定磁场有旋性的直接证明
B A ( A) 2 A
2 A 0 2 Jc (r) dV
11-6 安培环路定理
d
B1
I
r1
B2 dl 2 dl1
0 I 0 I B1 dl1 r1d d 2 r1 2π
r2
0 I 0 I B2 dl2 r2 d d 2 r2 2π
l
B1 dl1 B2 dl2 0 B d l 0
L4
第十一章 恒定磁场
11 – 6 安培环路定理
B dl 0
L
④ 穿过 L 的电流： 对 B 和 LB dl 均有贡献 不穿过 L 的电流： 对 L 上各点 B 有贡献 对 LB dl 无贡献 B : 与空间所有电流有关 B 的环流： 只与穿过环路的电流代数和有关
(1) 回路 L 内的 I (2) 回路 L 内的 I (3) 回路 L 内的 I (4) 回路 L 内的 I
第十一章 恒定磁场
不变， L 上各点的B 不变. 不变， L 上各点的B 改变. 改变， L 上各点的B 不变. 改变， L 上各点的B 改变.
11 – 6 安培环路定理
l
R R
L
r
2π r 2 πr 0 r R B d l 0 I 2 l πR 2 0 Ir 0 r B 2π rB 2 I 2 2π R R
第十一章 恒定磁场
B
0 I
B
dB
I
.
dI
B
11 – 6 安培环路定理
B
的方向与 I 成右螺旋
0 r R,
例 如图，流出纸面的电流为 2 I ，流进纸面的电 流为 I ，则下述各式中哪一个是正确的? （） (1)
(2) (3) (4)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
密度为 J ，求两圆柱重叠部分的磁感应强度。
解：
C B dl 0 I
y
左边圆柱
2 r1 B1 0 r12 J
B1
a1
0 r1J
2
右边圆柱
r1
r2
O1 d
O2
x
2 r2 B2 0 r22 J
B2
a2
0 r2J
2
B B1 B2
0 J
2
d
r ay
电磁场理论基础第四章
电磁场理论基础第四章
B A yax A xay
是否可能是某区域
的磁感应强度?若是,求相应的电流分布。
例3：证明矢量磁位A1
ax cos y ay sin x
和 A2
ay
sin x
x sin
y
给出相同的磁感应强度，并证明它们得自相同的电流分布。
它们是否满足矢量泊松方程，为什么？
例4：两个半径为 a 的圆柱体，轴间距为 d ，d 2 a 。除两
例5：半径为
a
的长圆柱面上有密度为
J
的面电流，分别求
S
下述两种情况下的圆柱内、外的磁感应强度。
⑴
电流方向沿
a
方向；
⑵
电流方向沿
az
方向。
解： ⑴
B
az
Bz
r
在圆柱内、外， B 0
B
a
Bz r
0
由此可知，磁场是一个与 ，z 和 r 无关的常量。
⑵
电磁场理论基础第四章
例2：判断矢量函数
圆柱重叠部分外，柱内有大小相等，方向相反的电流，
密度为 J ，求两圆柱重叠部分的磁感应强度。
二、矢量磁位的计算 1、直接应用矢量磁位的计算公式。
2、求解矢量磁位的泊松方程或拉普拉斯方程。
三、电流的计算
四、磁通量的计算
五、力的计算
电磁场理论基础第四章
例2：判断矢量函数
B A yax
Axay
是否可能是某区域
的磁感应强度?若是,求相应的电流分布。
解：
由
B
0
，可知此矢量函数可以是某区域的
和
A2
ay
sin x
x sin y
给出相同的磁感应强度，并证明它们得自相同的电流分布。
它们是否满足矢量泊松方程，为什么？
解：
1
1
J1 0 B1
0
a x cos y a y sin x
J2
1
0
B2
1
0
a x cos y a y sin x
2 A1
2
ax
cos
的磁场。
B
解：
l B d l 0I
B
2B l 0 JSl
B 0 JS
2
在平面上方：B
0J
2
S
ax
在平面下方：
B
0J S
2
ax
dB2 y
dB
P
dB1 d
dl2
o
a
lc
dl1
x
b
真空中恒定磁场的计算：
电磁场理论基础第二章
一、磁感应强度的计算 1、直接应用磁感应强度的计算公式。 2、应用安培环路定理。 3、由矢量磁位的旋度求。
磁感应强度。
ax
ay az
J
1
0
B
1
0
x
y z
Ay Ax 0
2A
0 az
电磁场理论基础第四章
例3：证明矢量磁位 A1
ax
cos
y ay
sin x
和
A2
ay
sin x
x sin y
给出相同的磁感应强度，并证明它们得自相同的电流分布。
它们是否满足矢量泊松方程，为什么？
y ay
sin x
ax cos y a y sin x 0J1
2 A2
2
ay
sin
x
x sin
y
ay
sin
x
x
sin
y
0J2
这是由于 A1 满足库仑规范，而 A2不满足库仑规范。
电磁场理论基础第四章
例4：两个半径为 a 的圆柱体，轴间距为 d ，d 2 a 。除两
圆柱重叠部分外，柱内有大小相等，方向相反的电流，
第四章 恒定磁场
4.1 安培定理与磁感应强度 4.2 恒定磁场的散度和矢量磁位 4.3 恒定磁场的旋度 4.4 物质的磁化 4.5 恒定磁场的基本方程 4.6 标量磁位 4.7 边界条件
B A
A
2
A
A 0
2
A
2
A
0J
0J
B 0J
安培环路定律的微分形式
S B dS S 0J dS
C B dl 0I
安培环路定律的积分形式
B
0 I 2r
a
证明：
C
B dl
0I
1、安培环路与磁力线重合
d
dl
B
rB
C
2、安培环路与磁力线不重合
z
l 2
R
dz z r r
0
l2 I
3、安培环路不交链电流
C B dl 0
M(,, z)
C
4、安培环路与若干根电流交链 C B dl 0 Ik
Px, y, z
r
C
例题：求无限长同轴线 各处的磁感应强度。
r B
0 Ir 2 a2
r a
ra
c ba
z
r
r B
0 I 2 r
r a
arb
r B
0 I 2 r
1
r2 c2
b2 b2
r a
r
B0
cr
brc
Br
0 I 2a
0 I 2b
a bc
例题：计算电流面密度为 JS的
无限大的均匀电流平面
解：
ax
ay az
B1 A1 x
y
z
az
cosy sin x 0
ax
ay
B2 A2 x
y
az
az
cos
x
sin
y
z
0 sin x x sin y 0
显然，两者的磁场相同。
电磁场理论基础第四章
例3：证明矢量磁位 A1
ax
cos
y ay
sin x