用matlab画分段函数y
MATLAB求分段函数最大值如何用MATLAB求分段函数的最小值和最大值

MATLAB求分段函数最大值如何用MATLAB求分段函数的最小值和最大值分段函数是一个由多个子函数组成的函数,每个子函数在定义域的不同区间上有不同的定义。
它通常用于描述真实世界中的非连续现象,如电子设备的开关状态或者非线性系统的行为。
要用MATLAB求解分段函数的最小值和最大值,我们可以按照以下步骤进行:1. 定义分段函数。
首先,我们需要将分段函数表示为一个MATLAB函数。
这可以通过使用if-else语句来实现。
以一个简单的分段函数为例,假设我们要计算以下分段函数在定义域[0,10]上的最小值和最大值:f(x)=x^2,0<=x<5f(x)=10,5<=x<=10我们可以用以下代码来定义这个分段函数:```function y = piecewise_function(x)if x >= 0 && x < 5y=x^2;elseif x >= 5 && x <= 10y=10;elsey=NaN;%处理定义域之外的情况endend```2.创建一个数值范围。
要计算分段函数的最小值和最大值,我们需要在定义域内创建一个数值范围。
在本例中,定义域为[0,10],我们可以用以下代码来创建一个包含许多离散点的数值范围:```x_range = linspace(0, 10, 100); % 在0到10之间创建100个离散点```这将创建一个包含100个离散点的向量x_range,这些点均匀分布在[0,10]之间。
3. 计算分段函数的值。
使用定义的数值范围和分段函数定义的MATLAB函数,我们可以计算每个离散点的函数值。
我们可以使用一个for 循环来实现这一点:```y_values = zeros(1, length(x_range)); % 创建一个包含每个离散点函数值的向量for i = 1:length(x_range)y_values(i) = piecewise_function(x_range(i));end```这将计算每个离散点的函数值,并将它们存储在一个向量y_values 中。
matlab大m法分段函数

matlab大m法分段函数MATLAB大M法是解决非线性规划问题的一种常用方法,也称为“大M惩罚因子法”或“人工变量法”。
该方法的基本思想是通过引入人工变量和一个大的正的M值,将原问题转化为一个辅助问题,然后通过寻找辅助问题的最优解来近似原问题的最优解。
具体来说,MATLAB大M法可以用于求解如下形式的非线性规划问题:最小化f(x)约束g(x)≤0h(x)=0lb ≤ x ≤ ub其中,f(x)为目标函数,g(x)≤0为不等式约束条件,h(x)=0为等式约束条件,lb和ub为变量x的下界和上界。
MATLAB大M法的基本步骤如下:1. 将目标函数和约束条件转化为标准形式:将不等式约束条件g(x)≤0和变量x的上下界lb≤x≤ub转化为等式约束条件:g(x)+s=0,其中s为松弛变量;lb - x = 0,其中x为原变量,lb为下界;x - ub = 0,其中x为原变量,ub为上界。
2.引入人工变量和大M值:对于每个不等式约束条件g(x)≤0,引入人工变量a和大的正的M值,得到约束条件:g(x)+s-Ma≤0;a≥0。
3.构建辅助问题:将目标函数加上大M值乘以人工变量,构造辅助问题:最小化f(x)+Ma4.求解辅助问题:使用MATLAB等工具求解辅助问题,得到辅助问题的最优解x*和人工变量的最优解a*。
5.判断辅助问题的最优解:若辅助问题的最优解中a*>0,则说明原问题无可行解,结束算法;否则,继续进行下一步。
6.去除人工变量:在原问题中去除人工变量a,即将约束条件g(x)+s-Ma≤0中的人工变量a去除。
7.求解原问题:使用MATLAB等工具求解去除人工变量后的原问题,得到原问题的最优解x*。
通过以上步骤,可以利用MATLAB大M法求解非线性规划问题。
需要注意的是,在设置大M值时需要选择一个足够大的值以确保人工变量a总是为0,同时又不至于导致数值问题或算法收敛困难。
另外,该方法适用于一般的非线性规划问题,但对于特定的问题可能存在更有效的求解方法。
Matlab建模训练3 图形绘制
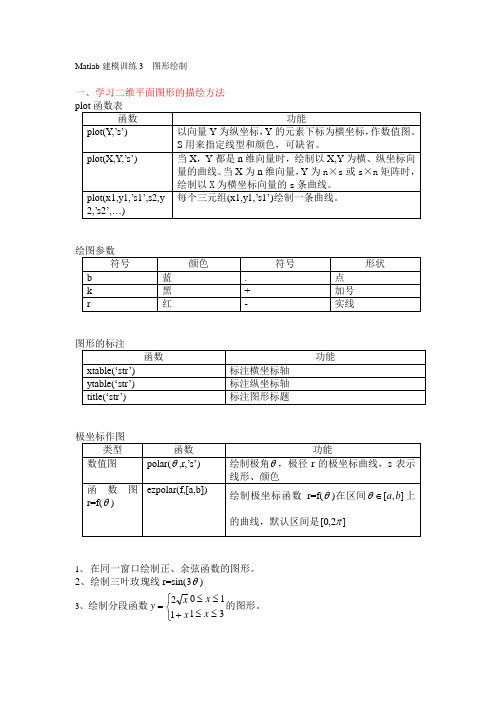
Matlab 建模训练3 图形绘制一、学习二维平面图形的描绘方法1、 在同一窗口绘制正、余弦函数的图形。
2、绘制三叶玫瑰线r=sin(3θ)3、绘制分段函数311012≤≤≤≤⎩⎨⎧+=x x xx y 的图形。
二、学习空间曲线的绘制1、sin cos cos ,06sin ,06.x t t x t ty t t t y t t t z t z tππ==⎧⎧⎪⎪=≤≤=≤≤⎨⎨==⎪⎪⎩⎩及2、 绘制空间曲线sin ,cos ,x t t y t z ===三、学习空间曲面的绘制例 绘制函数sin z x =4个子图的不同特征。
[X,Y]=meshgrid(-4:0.2:4); Z=X.*sin(sqrt(X.^2+Y .^2)); subplot(2,2,1) mesh(Z)subplot(2,2,2) mesh(X,Y ,Z) subplot(2,2,3)surf(X,Y,Z)subplot(2,2,4)surfc(X,Y,Z)ezsurf命令彩色表面图,调用格式与ezmesh相同。
二维图形的视例 分别用命令ezmesh(22,22x y -≤≤-≤≤)和ezsurf(04,14x y ≤≤-≤≤)作函数例 绘制函数22xy z xe --=的图形,并在各坐标设置点观察图形。
功能在默认区域0,2x y π≤≤上画z=f(x,y)高线图,a x y b ≤≤上画z=f(x,y)的等高线图,a x b c y d ≤≤≤≤上画z=f(x,y)例 绘制函数sin cos(),,,,2222z x x y x y ππππ⎡⎤⎡⎤=++∈-∈-⎢⎥⎢⎥⎣⎦⎣⎦的二维等高线和填充等高线。
例 绘制多峰函数()()()222222211351311053x y x y x y x z x ex y e e--+-+---⎛⎫=----- ⎪⎝⎭,在[][],,,x y ππππ∈-∈-上的图形以及二维等高线、二维填充等高线和三维等高线的图形。
利用Matlab绘制各类特殊图形的实例代码

利⽤Matlab绘制各类特殊图形的实例代码Matlab绘图介绍强⼤的绘图功能是Matlab的特点之⼀,Matlab提供了⼀系列的绘图函数,⽤户不需要过多的考虑绘图的细节,只需要给出⼀些基本参数就能得到所需图形,这类函数称为⾼层绘图函数。
此外,Matlab还提供了直接对图形句柄进⾏操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、⽂字等)看做⼀个独⽴的对象,系统给每个对象分配⼀个句柄,可以通过句柄对该图形元素进⾏操作,⽽不影响其他部分。
Matlab绘制特殊图形1. 绘制极坐标图说明:使⽤polarplot函数绘制极坐标图,每组数据表⽰⼀条闭合曲线,共有20条曲线构成20条封闭同⼼曲线。
t = linspace(0,2*pi,500);y = 1+0.3*sin(20*t)+0.1*sin(30*t)+0.1*sin(40*t);polarplot(t,y,t,1.1*y,t,1.2*y,t,1.3*y,t,1.4*y,t,1.5*y,t,1.6*y,t,1.7*y,t,1.8*y,t,1.9*y,...t,2.0*y,t,2.1*y,t,2.2*y,t,2.3*y,t,2.4*y,t,2.5*y,t,2.6*y,t,2.7*y,t,2.8*y,t,2.9*y,'linewidth',1.5);2. 单条曲线绘制分段函数(反⽐例函数y=1/x)说明:反⽐例函数在x接近于0时,趋近于奇异(1/0 趋近于⽆穷⼤),使⽤nan⾮数对图形进⾏镂空,可以实现⼀条曲线绘制y=1/x的整个定义域。
x = linspace(-3,3,500);f = @(x) 1./x;y = f(x);for ii = 1:length(x)if abs(x(ii))<0.03x(ii) = nan;y(ii) = nan;endendplot(x,y)legend('y=1/x')3. 正⽅体内绘制随机分布的颜⾊⽚图说明:使⽤plot3绘制正⽅体12条边,使⽤fill3函数绘制颜⾊⽚,颜⾊⽚位置和填充颜⾊随机⽣成。
浅谈分段函数在Matlab下图像画法

理论探讨浅谈分段函数在M a tla b下图像画法赵丹时文俊(郑州升达经贸管理学院基础咅卩,河南郑州451191 )【摘要】继《M a t l a b分 数图像画法的几点注记》后,继续探讨了应用M a t l a b实现分段函数的另外两种画法,并将图像 平 广到三 中来。
【关键词】M a t l a b软件;分 数;图像数学的三大软件分别为M a t l a b,M a t h e m a t i c a,M a p l e,而M a t a l b作为数 件之一,用 的。
它具有强大的作图功能,能处理各种数 数 ,准确的 的型、颜色、数据等,因为了更好的将数学运用活和习,学好M a t l a b是必不 的。
我们在实际 的处过程中经常会 数 ,尤其分数的 ,我们在这里 下分 数在M a t l a b软件下的 。
《M a t l a b教程及实训》中关于用M a t l a b画分 数图的程序有些不妥,这种情况 后的习题中也有所体现,分析如下:根据函数绘制一条曲线,函数为『0.5e_0.5#2-3"2-""+# > 1! (", #)={0.7e_#2-6"2-1<"+j"1[0.5e-0%#2-3"2+"x+y"-1程序如下:x=0 :0.1 :10;y= x;i f(x+ y)>1z= 0.5 # e xp(-0. 5 # y."2 - 3 # x.r-x);e ls e iZ(x+y)<=K1z= 0.5 # e xp(-0. 5 # y."2 - 3 # x.r+ x);e ls ez= 〇.7 # e x p % -y."2-6#y."2);e n d:lo t3 (乂,y,z)该程序中不仅 输 误,逻辑错误,我们来分析一下原因:(1)第一个i f语句的条件判断(x+ y)> 1,也 (x+y)行 之和里的所有的 全部 1,条件的逻辑判断才会真,为假。
matlab分段函数求不定积分

matlab分段函数求不定积分以MATLAB分段函数求不定积分为题,我们将探讨如何使用MATLAB 来计算分段函数的不定积分。
分段函数是由多个不同的函数组成的函数,每个函数在不同的区间内定义。
计算分段函数的不定积分可以分为两个步骤:确定函数的定义域和求解每个定义域上的不定积分。
我们需要确定分段函数的定义域。
定义域是指函数在哪些区间上有定义。
例如,我们考虑一个简单的分段函数:f(x) = 2x, 当x < 0f(x) = x^2, 当x >= 0在这个例子中,函数的定义域可以分为两个区间:x < 0和x >= 0。
在MATLAB中,我们可以使用if语句来表示分段函数的定义域:```matlabfunction y = f(x)if x < 0y = 2*x;elsey = x^2;endend```接下来,我们需要求解每个定义域上的不定积分。
不定积分是指对函数进行积分得到的结果,不包含上下限。
在MATLAB中,我们可以使用int函数来计算不定积分。
对于上面的例子,我们可以使用以下代码来计算不定积分:```matlabsyms xif x < 0F = int(2*x, x);elseF = int(x^2, x);end```在这个例子中,我们使用了符号变量x来表示变量。
然后,我们使用if语句来根据x的值选择不同的积分表达式。
最后,我们将结果保存在变量F中。
需要注意的是,MATLAB中的int函数只能计算符号函数的不定积分,而不是数值函数的不定积分。
如果我们想要计算数值函数的不定积分,我们需要使用数值积分方法,如梯形法则或辛普森法则。
例如,假设我们想要计算函数f(x) = 2x在区间[0, 1]上的不定积分。
我们可以使用trapz函数来计算梯形法则的不定积分:```matlabx = linspace(0, 1, 100);y = 2*x;F = trapz(x, y);```在这个例子中,我们使用linspace函数生成了一个包含100个点的等间距向量x,表示区间[0, 1]。
分段函数的运算与可视化的MATLAB实现

fntnvl vnpi s g A L B. 1 曲 t U fr yM T A e u e tn fid f uco a eig e o t i T A nuu h G I e db A L Bt m ri s ns i u ni nun M 0 e o e h n ao ok o
维普资讯
20 牟g2 0 6 1期
中圈分类号 :P0 . T 3 16 文献标 识码 : A 文章 编号 :09— 52 2o )2 13— 3 10 25 (o6 1 —0 1 0
分 段 函数 的运 算 与 可视 化 的 M T A A L B实 现
。 _
柏 瞳 .tl ̄lt ll t l i i
1 操作界 面与功能
为了方便工程技术人员求解分段函数 的问题 。 使工程技术人员等使用用户只须输入分段函数的表 达式就可得出所需要 的运算结果 。本 文探讨 运用
MA L B的 图形用 户 界 面 ( U ) 程 实现 分 段 函 数 TA G I编
吴 晟 ,李开友 斌 ,罗 ,郭 洪
(.昆明理工大学信息工程与自动化学院,昆明 605;2 1 5 1 .四川机电学院,攀枝花 670) 0 100
摘
要 :探 讨 了应 用 M T_ AI AB实现分 段 函数 的绘 图并 求 出给 定 点处 的 函数 值 。通 过 MA I TAB提
,
Ab t a t T i p p r i u s d ta o e l e te p o o e s b e t n fn t n a d n me a o ft e sr c : h s a e s se l t w t rai l lt ft u s ci ci n u r t n o 1 d c 1 h o z 1 h o u o i I
高等数学实验matlab

式函数a0+a1x+a2x2作为经验公式n ),此时偏差平方和函数为
W=
(a
0
+a1xi
+a
2
x
2 i
-yi
)
2
i=1
其中n为数据点的数目。要使偏差平方和函数W最小,需要
n
n
n
na0 a1 xi a2 xi2 yi
i 1
i 1
i 1
a0
n
xi a1
n
xi2 a2
n
xi3
即拟合函数为 y=14.7391+0.1973139x-0.000339492x2
从图1-10可以看出拟合效果比较好,但是是否还可以更好呢? 一般而言,拟合次数的提高可以使得拟合效果变好,但是并 不是次数越高越好。现在提高拟合次数,将基函数由1,x,x2 修改为{1,x,x2,x3}(三次拟合),{1,x,x2,x3,x4}(四次拟合 )……,得到拟合图1-5至图1-9。
67
101
135
202
259
336
404
25.72
32.29
34.03
39.45
43.15
43.46
40.83
471 30.75
【实验方案】
设y代表土豆产量,x代表氮肥的施肥量。显然,y和x之间应该 有某种关系,假设y与x之间的关系为函数关系,则问题就转 化拟为合已问知题数。据点(xi,yi)位置关系,寻找函数y=y(x)。这就是数据
设计性实验
实验一 数据拟合问题 实验二 复利问题
第1章函数与极限—设计性实验
实验一 数据拟合问题
【实验目的】 1.加深对函数基本概念的理解 2.讨论了函数的实际应用问题 3.掌握Matlab软件中有关函数、画图等命令 【实验要求】 掌握函数基本知识,Matlab软件
