气体热现象的微观意义
高二物理气体热现象的微观意义
(3)从总体上看气体分子沿各个方向运动的机 会均等,因此对大量分子而言,在任一时刻向 容器各个方向运动的分子数是均等的。 (4)大量气体分子的速率是按一定规律分布, 呈“中间多,两头少”的分布规律,且这个分 布状态与温度有关,温度升高时,平均速率会 增大。
二.气体压强微观解释
1.气体压强是大量分子频繁的碰撞容器壁而产生 的. 2.影响气体压强的两个因素: (1)气体分子的平均动能,从宏观上看由气体的温 度决定.
例1.从微观领域解释:一定质量的理想气体,在 状态发生变化时,至少有两个状态参量同时发 生变化,而不可能只有一个参量发生变化,其它 两个参量不变.
例2.对一定质量的理想气体,下列四个论述中正 确的是( B ) A.当分子热运动变剧烈时,压强必增大 B.当分子热运动变剧烈时,压强可以不变 C.当分子间的平均距离变大时,压强必变小 D.当分子间的平均距离变大时,压强必变大
例3.关于地面附近的大气压强,甲说:”这个压强 就是地面每平方米面积的上方整个大气柱的压 力,它等于该气柱的重力”,乙说:”这个压强是 由地面附近那些做无规则运动的空气分子对每 平方米地面的碰撞造成的”,丙说:”这个压强既 与地面上方单位体积内气体分子数有关,又与地 面附近的温度有关” .你认为( ) A A.只有甲的说法正确 B.只有乙的说法正确 C.只有丙的说法正确 D.三种说法都有道理
一.气体分子运动的特点
(1)气体间的距离较大,分子间的相互作用力十分微 弱,可以认为气体分子除相互碰撞及与器壁碰撞外不受 力作用,每个分子都可以在空间自由移动,一定质量的 气体的分子可以充满整个容器空间,无一定的形状和体 积。 (2)分子间的碰撞频繁,这些碰撞及气体分子与器壁
的碰撞都可看成是完全弹性碰撞。气体通过这种碰撞 可传递能量,其中任何一个分子运动方向和速率大小 都是不断变化的,这就是杂乱无章的气体分子热运动。
理想气体的压强及温度的微观解释

理想气体的压强及温度的微观解释在普通物理热学的教学中,对理想气体的压强、温度的学习和讨论时,学生对压强、温度的微观实质理解困难,特别是对宏观规律的微观解释与分析问题。
文章从理想气体分子模型的建立和统计假设的提出,对压强、温度的实质进行讨论,从而使学生得到正确理解,并学会用微观理论解释和研究宏观现象和规律的分析方法。
标签:理想气体;微观模型;压强;温度;微观本质在物理的学习和研究中,经常会讨论和分析一些物理现象和规律,很多物理现象和规律,是可以通过实验观察和验证的宏观规律,而表征分子、原子运动性质的微观量,很难用观察或实验直接测定。
宏观量与微观量之间必然存在着联系,要更深入地认识和研究宏观规律,必须对宏观规律的微观本质进行分析。
通过对理想气体的几个宏观规律与微观实质的关系对比和分析,帮助我们认识和理解气体动理论的有关规律,并掌握这一研究方法。
1 理想气体模型及状态方程1.1 理想气体模型。
所谓理想气体是指重力不计,密度很小,在任何温度、任何压强下都严格遵守气体实验定律的稀薄气体。
理想气体是一种理想化的物理模型,是对实际气体的科学抽象。
理想气体的微观特征是:分子间距大于分子直径10倍以上,分子间无相互作用的引力和斥力,分子势能为零,其内能仅由温度和气体的量决定,内能等于分子的总动能。
温度提高,理想气体的内能增大;温度降低,理想气体的内能减小。
实际气体抽象为理想气体的条件:不易被液化的气体,如氢气、氧气、氮气、氦气、空气等,在压强不太大、温度不太低的情况下,所发生的状态变化,可近似地按理想气体处理。
分子本身的线度与分子之间的距离相比可忽略不计,视分子为没有体积的质点;除碰撞瞬间外,分子之间及分子与容器壁之间没有相互作用力,不计分子所受的重力;分子之间及分子与器壁之间作完全弹性碰撞,没有能量损失,气体分子的动能不因碰撞而损失。
容器各部分分子数密度等于分子在容器中的平均密度n=NV,式中,n是气体分子数密度,N是气体的总分子数,V是气体容器的容积;沿空间各个方向运动的分子数目是相等的;气体分子的运动在各个方向机会均等,不应在某个方向更占优势,即全体分子速度分量vx、vy和vz的平均值vx=vy=vz=0。
3.6热力学第二定律的微观意义
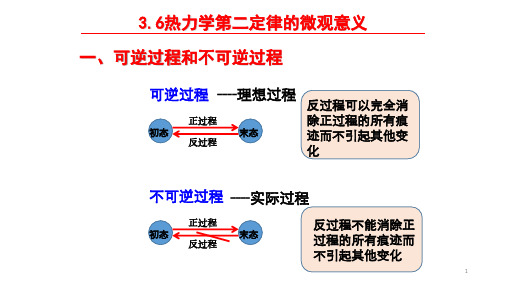
初态
末态
正过程反过程
反过程可以完全消除正过程的所有痕迹而不引起其他变化
初态
末态
正过程反过程
反过程不能消除正过程的所有痕迹而不引起其他变化
可逆过程不可逆过程----理想过程
----实际过程
3.6热力学第二定律的微观意义
一、可逆过程和不可逆过程
★如何判断一个过程是否可逆?
准静态绝热膨胀
可逆!
A C
B
Q
绝热自由膨胀
A
不可逆!有且仅有准静态、无能量耗散的过程是可逆过程。
二、热力学第二定律的微观意义
1.实质
一切与热现象有关的实
际宏观过程都是不可逆
的。
★落叶永离,覆水难收,逝
者如斯…都是不可逆过程。
2.统计规律
不可逆性是分子微观统计行为的宏观表现。
从微观上看,任何热力学过程总包含大量分子的无序运动状态的变化。
热力学第二定律指明大量分子运动的无序程度的变化规律:自然过程总是沿着大量分子运动从有序状态向无序状态变化的方向进行。
典型案例:
隔
板
A中:四个理想气体分子(N=4) B中:真空
A
B
614
4
11/164/16
4/16
1/16
6/16
A B
热力学第二定律的微观意义:
孤立系统内部所发生的过程,总是由热力学概率小(包含微观态数目少)的宏观态向热力学概率大(包含微观态数目多)的宏观态方向进行。
气体的温度与分子运动

气体的温度与分子运动气体是物质存在的状态之一,其特点是分子之间的间隔较大,分子运动自由而混乱。
气体的温度与分子运动之间存在着密切的关系,温度的升高会使气体分子的运动速度增加,而温度的降低则会导致气体分子的运动速度减慢。
本文将探讨气体的温度与分子运动之间的关系,并从微观角度解释这一现象。
一、气体的分子运动气体分子是以高速无规则运动的方式存在的。
根据动理论,气体分子不断地做无规则的热运动,具有三种基本运动状态:平动、转动和振动。
其中平动是最主要的运动形式,指的是分子在容器内的直线运动。
分子的平动速度与运动趋势是完全随机的,没有特定的方向。
二、气体温度的概念气体温度是指气体中分子热运动状态的一种表征,它反映了气体分子的平均动能。
温度的高低决定了分子热运动的剧烈程度。
通常,我们使用摄氏度(℃)或开尔文(K)来表示气体的温度。
三、温度与分子平均动能的关系根据气体动理论,气体分子的平均动能与温度成正比。
具体来说,当温度升高时,气体分子的平均动能也会增加;反之,温度降低时,气体分子的平均动能减少。
这是因为温度的增加意味着气体分子获得更多的热能,分子的平均速度也会增加。
在恒定体积下,气体分子的速度增加意味着分子碰撞的频率增加,分子间碰撞的力量也会增强。
同时,分子速度的增加也增加了分子与容器壁之间的碰撞频率和力量,从而增加了气体的压力。
四、温度与分子速度的关系温度与气体分子速度之间存在一定的关系。
根据麦克斯韦-玻尔兹曼分布定律,分子速度与温度之间的关系可以用以下公式表示:v = √(2kT/m)其中,v代表气体分子的速度,k为玻尔兹曼常数,T为温度,m为气体分子的质量。
由于速度与温度成正比,所以当温度升高时,分子速度也会增加。
这与我们前面提到的气体分子的平均动能与温度成正比的结论相一致。
五、温度对气体性质的影响温度的变化对气体性质有着明显的影响。
温度的升高会使气体分子的运动更加剧烈,气体分子之间碰撞的频率和力量增加,导致气体的压力增大。
气体微观解释

气体是由分子或原子组成的物质的一种状态。
在气体状态下,分子或原子之间存在大量的间隙,它们以高速运动,并且彼此之间相互碰撞。
气体的微观解释涉及到以下几个方面:
1.分子运动:气体分子以高速无规则运动,沿直线路径做匀速直线运动,同时也做碰撞运动。
这种运动是随机的,即分子的速度和方向是无规则的。
2.分子间相互作用:在气体状态下,分子之间存在较弱的相互作用力,通常为范德华力。
由于这种力较弱,分子之间的距离较大。
因此,气体分子间相互作用力的影响相对较小。
3.分子间碰撞:由于分子的高速运动和无规则运动,它们会频繁地相互碰撞。
这些碰撞是弹性碰撞,即在碰撞后分子的动能和总能量守恒,但方向和速度可能发生变化。
4.气体的体积:由于气体分子之间存在较大的间隙,并且分子运动是无规则的,气体没有固定的形状和体积,能够充满容器的全部可用空间。
综上所述,气体的微观解释是指气体分子的高速无规则运动、分子间相互作用力的较弱和碰撞的弹性特性。
这些特性使得气体表现出其宏观性质,如可压缩性、扩散性和可变形性。
热力学第二定律,微观解释

结论:内能不能全部转化为机械能,机械能可以全 部转化为内能
2、开尔文表述: 内能和机械能转化的方向性
不可能从单一热库吸收热量,使之完全变成 功,而不产生其他影响
3、第二类永动机:从单一热源吸收热量,使之 用来全部用来做功,而不硬气其他变化的热机
第二类永动机不能制成:违背热力学第二定律, 不违背能量守恒定律
热量不能自发地从低温物体传给高温物体。
热量可以从低温物体传给高温 物体吗?
电冰箱通电: 热量从低温物体传给高温物体 电冰箱断电: 热量从低温物体传温物体
高温热库
Q1 制冷机 Q2
w
低温热库
Q2 W Q1
能量守恒
高温热库
Q1 热机 Q2
热机效率:
w
W ≤100% Q1
低温热库
Q1 Q2 W
第一类永动机不能制成:违背能量守恒定律
练一练
4、能量耗散
人类没办法把流散掉的内能重新收集起来加 以利用的现象 能量耗散:能量数量不少,能量品质下降
热力学第一定律
热力学第二定律
热力学第二定律的微观解释
1.有序和无序
2.宏观态和微观态
宏观态:符合某种规定、规则的状态,叫做热力学系 统的宏观态。 微观态:在宏观状态下,符合另外的规定、规则的状 态叫做这个宏观态的微观态。
10.4热力学第二定律
10.5热力学第二定律的微观解释
热力学第二定律 一、结论:
1、一切涉及热现象的宏观自然过程都具有 方向性或都不可逆的 2、虽然一切宏观自然过程都满足能量守恒, 但不是符合能量守恒的过程都能真的发生 二、热力学第二定律
1、意义:反映宏观自然过程方向性的定律
2、克劳修斯表述: 热传导的方向性
一课一练气体热现象的微观意义

2011学年第二学期每课导学要点第4节气体热现象的微观意义主备人:王富根一、教学目标.在物理知识方面的要求:(1)能用气体分子动理论解释气体压强的微观意义,并能知道气体的压强、温度、体积与所对应的微观物理量间的相关联系。
(2)能用气体分子动理论解释三个气体实验定律。
.通过让学生用气体分子动理论解释有关的宏观物理现象,培养学生的微观想像能力和逻辑推理能力,并渗透“统计物理”的思维方法。
.通过对宏观物理现象与微观粒子运动规律的分析,对学生渗透“透过现象看本质”的哲学思维方法。
二、重点、难点分析.用气体分子动理论来解释气体实验定律是本节课的重点,它是本节课的核心内容。
.气体压强的微观意义是本节课的难点,因为它需要学生对微观粒子复杂的运动状态有丰富的想像力。
三、教具计算机控制的大屏幕显示仪;自制的显示气体压强微观解释的计算机软件。
【典型例题】气体压强大小反映了气体分子运动的哪些特征呢?这应从气体对容器器壁压强产生的机制来分析。
先让学生看用计算机模拟气体分子运动撞击器壁产生压强的机制:显示出如图1所示的图形:向同学介绍:如图所示是一个一端用活塞(此时表示活塞部分的线条闪烁3~5次)封闭的气缸,活塞用一弹簧与一固定物相连,活塞与气缸壁摩擦不计,当气缸内为真空时,弹簧长为原长。
如果在气缸内密封了一定质量的理想气体。
由于在任一时刻气体分子向各方向上运动的分子数相等,为简化问题,我们仅讨论向活塞方向运动的分子。
大屏幕上显示图2,即图中显示的仅为总分子数的合,(图中显示的“分子”暂呈静态)先看其中一个(图2中涂黑的“分子”闪烁2~3次)分子与活塞碰撞情况,(图2中涂黑的“分子”与活塞碰撞且以原速率反弹回来,活塞也随之颤抖一下,这样反复演示3~5次)再看大量分子运动时与活塞的碰撞情况:大屏幕上显示“分子”都向活塞方向运动,对活塞连续不断地碰撞,碰后的“分子”反弹回来,有的返回途中与别的“分子”相撞后改变方向,有的与活塞对面器壁相碰改变方向,但都只显示垂直于活塞表面的运动状态,而活塞被挤后有一个小的位移,且相对稳定,如图3所示的一个动态画面。
知识讲解 气体热现象的微观意义

气体热现象的微观意义【学习目标】1.知道气体分子的运动特点,知道气体分子的运动遵循统计规律.2.知道气体压强的微观意义.3.知道三个气体实验定律的微观解释.4.了解气体压强公式和推导过程.【要点梳理】要点一、统计规律1.统计规律由于物体是由数量极多的分子组成的,这些分子并没有统一的运动步调,单独看来,各个分子的运动都是不规则的,带有偶然性,但从总体来看,大量分子的运动却有一定的规律,这种规律叫做统计规律.2.分子的分布密度分子的个数与它们所占空间的体积之比叫做分子的分布密度,通常用n 表示.3.气体分子运动的特点(1)气体分子之间的距离很大,失约是分子直径的10倍.因此除了相互碰撞或者跟器壁碰撞外,气体分子不受力的作用,在空间自由移动.(2)分子的运动杂乱无章,在某一时刻,向着任何一个方向运动的分子都有,而且向各个方向运动的气体分子数目都相等.(3)每个气体分子都在做永不停息的运动,常温下大多数气体分子的速率都达到数百米每秒,在数量级上相当于子弹的速率.(4)气体分子的热运动与温度的关系○1温度越高,分子的热运动越激烈.○2理想气体的热力学温度T 与分子的平均动能k E 成正比,即:k T aE (式中a 是比例常数),因此可以说,温度是分子平均动能的标志.要点诠释:理想气体没有分子势能,所以其内能仅由温度决定,温度越高,内能越大,温度越低,内能越小.要点二、对气体的微观解释1.气体压强的微观意义(1)气体压强的大小等于气体作用在器壁单位面积上的压力.(2)产生原因:大量气体分子无规则运动碰撞器壁,形成对器壁各处均匀的持续的压力而产生.(3)决定因素:一定气体的压强大小,微观上决定于分子的平均动能和单位体积内的分子数;宏观上决定于气体的温度T 和体积V2.对气体实验定律的微观解释(1)一定质量的气体,分子的总数是一定的,在温度保持不变时,分子的平均动能保持不变,气体的体积减小到原来的几分之一,气体的密度就增大到几倍,因此压强就增大到几倍,反之亦然,所以气体压强与体积成反比,这就是玻意耳定律.(2)一定质量的气体,体积保持不变而温度升高时,分子的平均动能增大,因而气体压强增大,温度降低时,情况相反,这就是查理定律所表达的内容.(3)一定质量的气体,温度升高时要保持压强不变,只有增大气体体积,减小分子的分布密度才行,这就是盖一吕萨克定律所表达的内容.要点三、分子的平均动能1.分子的平均动能物体分子动能的平均值叫分子平均动能.温度是分子平均动能的标志,温度越高,分子平均动能越大.物体内部各个分子的运动速率是不相同的,所以分子的动能也不相等.在研究热现象时,有意义的不是一个分子的动能,而是物体内所有分子动能的平均值——分子平均动能.物体的温度是大量分子热运动剧烈程度的特征,分子热运动越剧烈,物体的温度越高,分子平均动能就越大,所以说温度是分子平均动能的标志这是对温度这一概念从物体的冷热程度的简单认识,进一步深化到它的微观含义、本质的含义.2.判断气体分子平均动能变化的方法(1)判断气体的平均动能的变化,关键是判断气体温度的变化,因为温度是气体分子平均动能的标志.(2)理解气体实验定律的微观解释关键在于理解压强的微观意义.要点四、宏观、微观的区别与联系1.宏观、微观的区别与联系从宏观上看,一定质量的气体仅温度升高或仅体积减小都会使压强增大,从微观上看,这两种情况有没有什么区别?分析:因为一定质量的气体的压强是由单位体积内的分子数和气体的温度决定的.气体温度升高,即气体分子运动加剧,分子的平均速率增大,分子撞击器壁的作用力增大,故压强增大.气体体积减小时,虽然分子的平均速率不变,分子对容器的撞击力不变,但单位体积内的分子数增多,单位时间内撞击器壁的分子数增多,故压强增大,所以这两种情况下在微观上是有区别的.2.气体压强的公式现在从分子动理论的观点推导气体压强的公式.设想有一个向右运动的分子与器壁发生碰撞(图8-5-1),碰撞前的速率为v ,碰撞前的动量为mv ,碰撞后向左运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过定量分析得出: ★ 通过定量分析得出:理想气体的热力学 温度T与分子的平均动能成正比 与分子的平均动能成正比. 温度 与分子的平均动能成正比
T = a Ek
a
为比例常数
★ 温度是分子平均动能的标志
● 气体压强 的微观意义 思考: 思考:
从微观角度看
1.气体对容器的压强 是如何产生的? 是如何产生的?
甲:我很怕坐飞机,我问过专家,每架飞机上 我很怕坐飞机,我问过专家, 有炸弹的概率是万分之一. 有炸弹的概率是万分之一.万分之一虽然 很小,但还没小到可以忽略不计的程度, 很小,但还没小到可以忽略不计的程度, 所以我以前从来不坐飞机。 所以我以前从来不坐飞机。 乙:可是你今天为什么来坐飞机了? 可是你今天为什么来坐飞机了 甲:我又问过专家,每架飞机上有一颗炸弹的概率是万分之一, 我又问过专家,每架飞机上有一颗炸弹的概率是万分之一, 但每架飞机上同时有两颗炸弹的概率只有亿分之一. 但每架飞机上同时有两颗炸弹的概率只有亿分之一.这已经 小到可以忽略不计了。 小到可以忽略不计了。 乙:但两颗炸弹与你坐不坐飞机有什么关系? 但两颗炸弹与你坐不坐飞机有什么关系? 甲:当然有关系啦.不是说同时有两颗炸弹的概率很小吗,我 当然有关系啦.不是说同时有两颗炸弹的概率很小吗, 现在自带了一颗炸弹,飞机上再有一颗几乎是不可能的, 现在自带了一颗炸弹,飞机上再有一颗几乎是不可能的, 所以我才放心地来坐飞机! 所以我才放心地来坐飞机! 乙:#¥%&…我和你想的一样,我也带了一颗! ¥ …我和你想的一样,我也带了一颗!
是大量气体分子频繁地碰撞 器壁而产生的
2.压强的大小可能和 什么因素有关? 什么因素有关?
“大米模拟实验”——气体压强的微观解释 大米模拟实验” 大米模拟实验 气体压强的微观解释
【实验一】 实验一】
在某高度, 将大米连续倒在秤盘上,观察示数 在更高的位置,将大米连续倒在秤盘上,观察示数 实验现象: 位置越高, 实验现象: 位置越高,台秤的示数越大 结论:大米的动能越大, 结论:大米的动能越大,对秤盘压强越大 类比:气体分子平均动能越大, 类比:气体分子平均动能越大,气体压强越大
}
–
气体压强增大(减小) 体压强增大(减小)
请自己解释查理定律和 请自己解释查理定律和盖—吕萨克定律 查理定律 吕萨克定律 ◆ 查理定律 一定质量的某种气体, 一定质量的某种气体,在体积不变的情 况下, 与热力学温度T成正比 况下,压强 p与热力学温度 成正比 与热力学温度 ◆ 盖—吕萨克定律 吕萨克定律 一定质量的某种气体, 一定质量的某种气体,在压强不变的情 况下,其体积V与热力学温度 与热力学温度T成正比 况下,其体积 与热力学温度 成正比
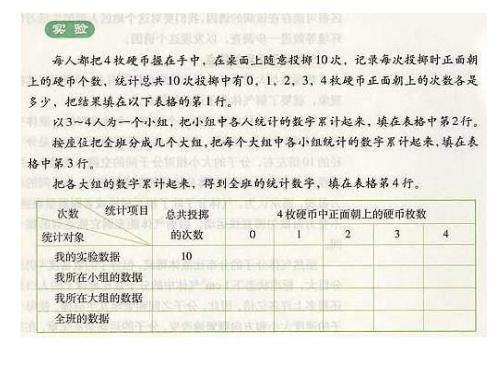
次数 统计对象 我的实验数据 我所在大组的数据 全班的数据 统计项目 总共投掷 的次数 10 4枚硬币中正面朝上的硬币枚数 0 1 2 3 4
上面的实验给我们什么启示? 上面的实验给我们什么启示
1、个别随机事件的出现具有偶然性 、 2、大量随机事件的整体会表现出一定的 、
规律性
这种规律就是统计规律
三、气体热现象的微观意义 ● 气体温度 的微观意义
图象观察与思考
1、 图中氧气分子速率分布是否 、 存在统计规律? 存在统计规律? 存在统计规律 2、 0℃和100℃氧气分子速率分 、 ℃ ℃ 布有什么相同的统计规律? 布有什么相同的统计规律? 都呈中间多两头少的分布规律 3、 对比 ℃和100℃氧气分子速率 、 对比0℃ ℃ 分布图象,有什么不同? 分布图象,有什么不同? 温度越高, 温度越高,分子平均速率越大
掷币实验
【实验目的】研究随机事件的出现是否存在规律性 实验目的】 实验方法】 【实验方法】 1、将4枚硬币握在手中,在桌面上随意投掷10次。 、 枚硬币握在手中,在桌面上随意投掷 次 枚硬币握在手中 2、记录每次投掷时正面朝上的硬币数。 、记录每次投掷时正面朝上的硬币数。 3、统计共10次投掷中有 、1、2、3、4枚硬币正面朝上的 、统计共 次投掷中有 次投掷中有0、 、 、 、 枚硬币正面朝上的 次数,并将结果填入表格中。 次数,并将结果填入表格中。
▲气体分子的平均动能 (温度) 温度) 体积) ▲气体分子的密集程度 (体积)
● 对气体实验定律 的微观解释 ◆ 玻意耳定律
一定质量的气体,在温度不变的情况下,压强 与 一定质量的气体,在温度不变的情况下,压强p与 体积V成反比
▲ 玻意耳定律的微观解释
T不变 不变 V减小 减小 增大) (增大) 分子平均动能不变 分子密集程度 增大(减小) 增大(减小)
课后作业: 课后作业 1.阅读课本 29《科学漫步》 阅读课本P 科学漫步》 阅读课本 2.想一想生活中表现统计规律的事例 想一想生活中表现统计规律的事例
一、随机性与统计规律
1、在一定条件下,若某事件必然出现,这个事件 、在一定条件下,若某事件必然出现, 叫做必然事件 2、若某件事不可能出现,这个事件叫做 、若某件事不可能出现 出现,
不可能事件
3、若在一定条件下某事件可能出现,也可能不出现, 、若在一定条件下某事件可能出现,也可能不出现, 这个事件叫做随机事件
温度
【实验二】 实验二】
在相同高度, 将大米更密集倒在 大米更密集倒在秤盘上,观察示数 大米更密集倒在 实验现象: 实验现象: 倒在秤盘上的大米越密集, 倒在秤盘上的大米越密集,示数越大
类比:气体分子越密集, 类比:气体分子越密集,气体压强越大 体积
结
论:
气体压强的大小跟两个因素有关: 气体压强的大小跟两个因素有关:
二、气体分子运动的特点
气体分子距离比较大, 分子间作用力很弱, ● 气体分子距离比较大, 分子间作用力很弱,分子除了相互 碰撞或跟器壁碰撞外不受力而做匀速直线运动, 碰撞或跟器壁碰撞外不受力而做匀速直线运动,因而会充满 它能达到的整个空间 ●气体分子数量巨大,之间频繁地碰撞,分子速度大小和方向 气体分子数量巨大,之间频繁地碰撞, 运动杂乱无章, 频繁改变 ,运动杂乱无章,任何一个方向运动的气体分子都 有,各个方向运动的分子数目基本相等
