量子化学第五章分子轨道理论
第五章量子化学

k s 1 p的成键能力 可求得 f
k
fk f s 1 f p 3(1 )
fk 大小随大小而变。
若α=0, 若α=1/4, 若α=1/2, 若α=3/4, 若α=1,
fk 3 1.732 f p
fk 2, 为fk 最大值
杂化轨道:在一个原子中不同原子轨道的线性
组合称为原子的轨道杂化 ,杂化后的原子轨道
称为杂化轨道。 杂化的目的:更有利于成键。 杂化的动力:受周围原子的影响。
杂化的规律 ★ 轨道的数目不变,空间取向改变 ;
★ 杂化轨道能与周围原子形成更强的σ键,或安 排孤对电子,而不会以空的杂化轨道存在。
杂化轨道理论的基本假定: (1)杂化轨道是参加杂化的原子轨道的线性组合, 其数学表达为:
,
BeCl2的分子结构。
BeCl2
Cl
Be:
2s
2p
Be
Cl
2s, 2p轨道
2p
2p
2s
2s
激发
sp
sp杂化
2p
BeCl 2的形成
Be采用sp杂化 -------生成BeH2
BeH2 Be sp杂化
S轨道要平均分配到两个杂化轨道中去,α=1/2,同 理β=1/2
1 3 F 3 1.932 2 2
第五章 多原子分子结构
5.1 杂化轨道理论
1. 杂化轨道理论提出的实验基础
• 1931年Pauling提出,为了解释键角的变化。
H2S:∠H-S-H=92º H2O:∠H-O-H=104.5º NH3:∠H-N-H=107º CH4:四个C-H键等价,键角109º 28'
2. 杂化轨道理论 杂化:中心原子轨道的线性组合
第五章_分子轨道理论

轨道进行简单的介绍。
四 、配位化合物中的分子轨道理论
要点:
A、配体原子轨道通过线性组合,构筑与中心原子 轨道对称性匹配的配体群轨道。 B、中心原子轨道与配体群轨道组成分子轨道。
金属与配体间σ分子轨道(d轨道能级分裂)
1.可形成σ分子轨道的中心原子轨道 在八面体配合物MX6中,每个配体可提供一个Pz 轨道用于形成σ分子轨道。
(2)分子轨道由原子轨道线性组合而成的,而且
组成的分子轨道的数目同互相化合原子的原子轨道
的数目相同。 (3)分子中电子的排布遵从原子轨道电子排布三 原则,即能量最低原理、泡利不相容原理和洪特规 则。
1. 原子轨道线性组合的方式
形成LCAO-MO的三原则:
linear combination of atomic orbital-molecular orbital
分子轨道理论的作用:
1. 可以解释包括羰基配合物、 π 配合物等特殊配合物 在内的配位键的形成;
2. 可以计算出所形成配合物分子轨道能量的高低;
3. 可以定量地解释配合物的某些物理和化学性质;
不足:
计算分子轨道能量的高低需要冗长的计算,非常繁琐;
通常采用简化或某些近似的方法来得到分子轨道能量的相对 高低。这里只定性地对常见的八面体配位构型配合物得分子
分子 H2 He2 He2+
键级
磁性
1s σ
1s
σ 1s*1 1s
分子 Li2 Be2 B2 C2 N2 O2 + O2 O2 F2 Ne2 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ 1s21s2σ
出的一个序列。 N2[(σ1s)2(σ1s*)2(σ2s)2(σ2s*)2(π2py)2(π2pz)2(σ2px)2]
第五章分子轨道理论

那
caa cbb
应用线性变分方法,则
ca (H aa E) cb (H ab ESab ) 0 ca (H ab ESab ) cb (Hbb E) 0
令
a H aa , b Hbb , H ab , 且忽略Sab
ccaa
(a
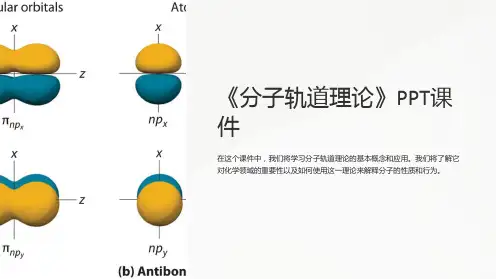
分子轨道按其对称性及特定的节面加以分类
通常分为 , , 等类型。
1、 分子轨道:对键轴呈圆柱形对称的分子轨道。
轨道
呈中心对称的轨道—成键 轨道 呈中心反对称的轨道—反键 轨道
如
np
np
成键 g ( p ) 反键 u ( p )
2、 分子轨道:对于一个含键轴的节面呈反对称的轨道。
轨道
呈中心反对称的轨道—成键 轨道 呈中心对称的轨道—反键 轨道
2 NM RNM 2 ij rij
排斥能
ZN
Ni rNi
核与电子的吸引势能
一、分子轨道:
分子轨道可由体系中原子轨道线性组合得到(LCAO)
n
ij ci1i1 ci2i2 cijij ,
j 1
i 1,2,
式中 ij 分子轨道 cij 组合系数 ij 原子轨道
分子轨道——分子中单个电子的运动状态(即单电子波函数)。 二、分子轨道形成的原则: MO可由AO线性组合得到:
只有对称性相同的AO才能组成MO。
S ab a* bd
对称性允许 + +
对称性不允许 -
++ -+-+
相长 相消
2、最大重叠原则:
从 h 的表达式中可看出,当 a b 一定时,
如 使得h
*a Hˆ bd ESab
《分子轨道理论》课件
1 分子轨道能级的定义 2 分子轨道能级的计算 3 电子在分子轨道中的
我们将学习分子轨道能级
方法
分布
的概念和定义。了解它们
我们将探讨计算分子轨道
我们将研究分子轨道中电
是如何描述分子中电子的
能级的方法,如分子轨道
子的分布规律和性质。了
能量和分布。
的线性组合和量子化学计
解电子在不同分子中的行
算方法。
为。
原子轨道的定义
我们将学习原子轨道的基本概念和定义。了解它们是如何描述原子中电子的运动状态和能量 分布。
原子轨道的分类
我们将讨论原子轨道的不同类型,例如s轨道,p轨道,d轨道和f轨道。每种轨道有不同的形 状和能量。
原子轨道的数量
我们将研究不同原子中轨道的数量。了解不同原子的电子排布和轨道填充规则。
第三章:分子轨道
结论
通过这个课件,我们总结了分子轨道理论的主要内容和意义。理解了它对化 学领域的重要作用,并学习了如何应用这一理论解释分子的行为和性质。
《分子轨道理论》PPT课 件
在这个课件中,我们将学习分子轨道理论的基本概念和应用。我们将了解它 对化学领域的重要性以及如何使用这一理论来解释分子的性质和行为。
第一章:引言
本章将介绍分子轨道理论的背景和意义。我们将探讨为什么要发展这一理论 以及它对我们理解化学反应和分子结构的重要性。
第二章:原子轨道
1
分子轨道的定义
我们将学习分子轨道的概念和定义。了解它们是如何描述分子中电子的运动和分布。
2
分子轨道的分类
我们将讨论分子轨道的不同类型,如σ轨道和π轨道。每种轨道对分子的性质和化学反应起着 不同的作用。
3
分子轨道的数量
第五章简单分子轨道理论.

0 1 x 1
0 0 0 1 x
1 0 0 1 0 x 1 1 x 1 0 0 1 x 1 x
x 4 3x 2 1 0 1 x 2 (3 5 ) 2
x 1 (3 5 ) 1.618,0.618 2
E1 a 1.618
E3 a 0.618
能级图
E
1 2
1
(1 2 )
E
E
2 (2)丁二烯。为简便起见,我们假定所有的键是等长的,每个碳原 子有一个未杂化的轨道,它们组成分子轨道
(1 2 )
a11 a22 a33 a44
x 1 0 0
x x1 0
1 x 1 0
E
由E即可求出a1与a2。 由E
H11 ( )S11 a1 H12 ( )S12 a2 0 H 21 ( )S 21 a1 H 22 ( )S 22 a2 0
由于
H11 H 22
m n
n
* C n En m n C n En Cm 2 m n n
E0 En (n 1,2,)
E E0 C n
2
C
n
2 n
1
E E0 * ˆ H d E 0
如果波函数没有归一化,则能量平均值 * ˆ H d E * d
E2 a 0.618
E4 a 1.618
由这些能量值即可求出每个原子轨道前面的系数。由久期行列式得 到下列的方程组:
a1 x a 2 0 a a x a 0 1 2 3 a 2 a 3 x a 4 0 a 3 a 4 x 0
分子轨道理论

分子轨道理论1. 引言分子轨道理论是化学中的一种重要理论,它用量子力学的原理解释了分子的电子结构和化学性质。
本文将介绍分子轨道理论的基本概念、应用以及相关的计算方法。
2. 基本概念2.1 原子轨道在分子轨道理论中,首先要了解的是原子轨道。
原子轨道是描述单个原子中电子运动的波函数。
根据量子力学的原理,一个原子可以存在多个不同的原子轨道,每个原子轨道都对应着不同的能量状态。
2.2 分子轨道当两个或更多个原子靠近形成化学键时,原子轨道会互相重叠,形成新的分子轨道。
分子轨道描述的是电子在整个分子中的运动状态。
根据分子轨道理论,分子轨道可以分为两类:成键分子轨道和反键分子轨道。
成键分子轨道对应着电子的主要分布区域,而反键分子轨道则对应着电子分布相对较少的区域。
2.3 分子轨道能级分子轨道能级与原子轨道能级类似,分子轨道的能量随着轨道的能级增加而增加。
有时,分子轨道能级之间会有一定的能隙,这种能隙反映了分子稳定性的特征。
3. 分子轨道的应用分子轨道理论可以解释大量的化学现象和性质,下面列举了几个常见的应用:3.1 化学键的形成分子轨道理论提供了解释化学键产生的机制。
当两个原子靠近并形成化学键时,原子轨道会发生线性组合形成分子轨道。
通过分子轨道理论,我们可以理解不同类型的化学键(如共价键、离子键和金属键)是如何形成的以及其性质的差异。
3.2 分子轨道的能级顺序分子轨道理论还可以预测分子轨道的能级顺序,从而解释分子的化学性质。
能级较低的分子轨道通常具有较高的稳定性,从而决定了分子的化学反应性质。
3.3 分子光谱在分子光谱中,分子轨道理论被广泛应用。
分子轨道理论可以解释分子在吸收或发射光的过程中所发生的能级跃迁,从而解释不同光信号的产生和分子结构的变化。
4. 分子轨道的计算方法4.1 原子轨道模型著名的原子轨道计算方法包括Hartree-Fock方法和密度泛函理论。
这些方法通过求解原子的薛定谔方程,得到原子轨道及其能量。
分子轨道理论教学课件
密度泛函理论
01
密度泛函理论是一种更高效的计算方法,它将多电子系统的薛 定谔方程简化为单电子系统的方程。
02
它通过电子密度而不是波函数来描述多电子系统,从而大大减
少了计算量。
密度泛函理论在计算化学中得到了广泛应用,可以用于预测分
03
子的电子结构和性质。
分子力学方法
1
分子力学方法是一种基于经典力学原理的计算方 法,它通过势能面来描述分子的运动。
分子轨道理论认为分子中的电子是在一系列的分子轨道上运 动,每个分子轨道都由一个波函数表示,描述了电子在分子 中的运动状态。
分子轨道理论的发展历程
分子轨道理论的起源可以追溯到20世纪初,当时科学家开始尝试用量子力学来描述 分子中的电子行为。
在20世纪30年代,德国物理学家马克思·玻恩和英国化学家罗伯特·玻恩等人发展了 分子轨道理论的基本框架,为后续的研究奠定了基础。
或能级表。
分子轨道能级与化学反应的关系
03
分子轨道能级与化学反应的活化能、反应速率和反应机理等密
切相关,是理解和预测化学反应的重要依据。
03
分子轨道的计算方法
哈特里-福克方法
01
哈特里-福克方法是分子轨道理论 中最早的数值计算方法,它基于 变分原理,通过求解薛定谔方程 来计算分子轨道。
02
该方法适用于较小的分子,但对 于较大的分子和复杂的化学环境 ,计算量会变得非常大。
原子轨道有特定的形状和取向,如球 形、哑铃形、纺锤形等,这些形状和 取向决定了原子中电子云的分布。
分子轨道的形成
1 2 3
分子轨道的概念
分子轨道是指由两个或多个原子轨道相互作用形 成的能量状态,是分子整体的运动状态。
(精品课件)7.分子轨道理论-new
H2:
1
ψ H2 = σ1s (1) + σ1s (2) = 2 ⎡⎣ϕ A,1s (1) + ϕ B,1s (1)⎤⎦ ⎡⎣ϕ A,1s (2) − ϕ B,1s (2)⎤⎦
S-S轨道 LCAO
5. 分子轨道理论:
p-p轨道LCAO σ键 σ* 键
π 键 π* 键
5. 分子轨道理论:
BO = 1 BO = 0.5 (三电子σ键 ) BO = 0 (不形成稳定分子)
He2分子不能稳定存在,但是He2+或He22+可以稳定存在
5. 分子轨道理论:
Li2
Be2
气体 r = 267.3 pm D= 101kJ/mol
不存在
5. 分子轨道理论:
顺 磁 性 成 单 电 子
B2只存在 π 键无 σ 键
2s AO of O
σs
MO of NO
00 NO
NO
5. 分子轨道理论:
5. 分子轨道理论:
5. 分子轨道理论:
5. 分子轨道理论:
共轭π键 离域π键 大 π键
Π
6 6
5. 分子轨道理论:
形成π键的电子不局限于两个原子的区域,而是在参加成键
的多个原子形成的分子骨架中运动,这种化学键称为离域π键。
若满足以下两个条件,就可形成离域π键:
(1) 成键的原子共面(或共曲面),每个原子可提供一个垂直
于平面的p轨道 。
(2) π电子数小于参加成键原子的p轨道总数的二倍。
离域π键一般用
Π
m n
表示,n为参与成键的原子轨道数,m为电
子数。
5. 分子轨道理论:
非键轨道 n : nonbonding molecular orbital 能量较之原子轨道基本不变的分子轨道。
分子轨道理论的基本概念
分子轨道理论的基本概念分子轨道理论是描述分子内电子结构的理论基础,是理解和预测分子性质的重要工具。
它通过对分子中电子行为的定量描述,为我们提供了深入理解分子结构和化学性质的途径。
本文将介绍分子轨道理论的基本概念,包括分子轨道的形成、分子轨道能级、分子轨道的排布规律等内容。
分子轨道分子轨道是描述整个分子内所有电子运动状态的波函数。
在分子轨道理论中,通过线性组合原子轨道(Linear Combination of Atomic Orbitals, LCAO)方法,可以得到分子轨道波函数。
例如,两个氢原子相互结合形成氢气分子的过程中,每个原子的1s轨道可以线性组合形成一个成键分子轨道和一个反键分子轨道。
这种过程称为成键和反键形成。
通过这种方式形成的分子轨道波函数,可以用来描述氢气分子内电子的运动状态。
分子轨道能级根据量子力学原理,不同类型的分子轨道具有不同的能级。
一般来说,成键分子轨道的能级较低,反键分子轨道的能级较高。
在填充电子时,按照Pauli不相容原理和Hund规则,电子会依次填充到较低能级的成键分子轨道上,直到所有电子填充完毕。
这种填充顺序决定了分子的稳定性和化学性质。
分子轨道排布规律根据对称性和能量原理,我们可以确定不同类型分子轨道在空间中的排布规律。
以双原子分子为例,通过简单的组合对称性和量子力学计算,可以得到成键σ、反键σ、成键π和反键π四种主要类型的分子轨道。
每一种类型的分子轨道在空间中具有特定形状和取向,并且对应着不同的能级。
分子轨道理论在实践中的应用凭借其对化学键性质和反应活性等方面的深刻认识,分子轨道理论在近现代化学研究中扮演了重要角色。
它被广泛应用于有机合成设计、催化剂设计、光催化材料设计等领域。
例如,在有机合成设计中,我们可以通过对不同配体结构下电荷传递与空间排布特性进一步加深对反应机制及活性位点与其实际功能之间关联作用进一步了解。
结论总之,分子轨道理论为我们提供了揭示和预测化学现象背后原理的新视角,并且在许多实际应用中发挥着重要作用。
第5章 分子轨道理论
久 期 方 程
8
3、H2+的线性变分法的解
c1 ac2 b
⑴、线性变分函数的选取
使ra<<rb和R,
则1 和1 0 rb R
H ˆ 12111 2 ra rb R
Hˆ 12 1
2
ra
薛定谔方程 (12 1)E
2
ra
则变分函数 ψ = c1φa+c2φb
9
⑵、久期方程 久期行列式及其解
时,具有键轴轴对称性,对键轴呈圆柱形对 称性 。
成键 g ( p ) 反键 u ( p )
31
σ轨道(同核分子)
2s-2s 反键 2s*/u2s 中心对称
成键 2s /g2s 中心反对称
2pz 2pz 反键 2pz */u2pz
成键 2zp/g2pz
异核双原子分子,不具中心对称性。
32
②、 轨道
σ分子轨道外,应同时考虑2s-2pz间的组合,即应
考虑两原子的 2sa,2sb,2pz,a2pzb,四个原子轨道组
合成四个σ分子轨道。 2pxa 2px, b2pxa 2px组b合形
成一对简并的π轨道 .
顺序: K2Kg2u1u3g1g3u
42
⒋O2+,O2,F2+,F2
O和F的2s和2pz能级差别较大,不必考虑2s2pz之间的作用. 分子轨道次序如下:
E * Hˆd (c1ac2b)H ˆc1ac2bd
*d
(c1ac2b)2d
c1 2
aH ˆad2c1c2 aH ˆbdc2 2 bH ˆbd c1 2 a 2d2c1c2 abdc2 2 b 2d
10
引入 :
HaaaH ˆadHbb bH ˆbd
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章分子轨道理论5.1 Hatree-Fock 方程Hatree-Fock 近似,也就是分子轨道近似,是量子化学中心之一,分子中的电子占据轨道,这是化学家头脑中很容易想到的。
首先,我们推导一下Hatree-Fock 方程。
由于绝大多数分子都是闭壳层的,因此我们都可以用单slater 行列式作为其波函数,即12N C f f f ψ=设我们有正交集i j ij f f δ= 则一、二阶约化密度矩阵为:'*'11111''111112''21212''112122(,)()()(,)(,)1(,;,)2(,)(,)i i ix x f x f x x x x x x x x x x x x x ρρρρρρ∧∧∧∧∧∧==∑改写一下(Dirac ):*'*'11122*'*'2122''1212()()()()12()()()()1[()()()()]2NNi i i i iiNNj j j j jjN i j i j i jj i i jf x f x f x f x f x f x f x f x f x f x f x f x f f f f ρ∧≠==-∑∑∑∑∑12(1)(1,2)1(1)[(1,2)(1,2)]2(1,2)(1,2)1[]2r r Ni i i j i j i j j i ii ji i i ii i i i Ni i i j i j i j j i iijE T h T g f h f f f g f f f f g f f f f g f f f f g f f E f h f f f g f f f f g f f ρρ∧∧∧∧≠=+=+--=+-∑∑∑∑因为i=j 时,=0不影响上式因此现在就是要利用变分法,看在限制i j ij f f δ=下,什么样i f 的会使E 最小,所以要利用Lagrange 乘子法:**()Nij i j ij ij iji ij ij Nij i jij ij iji j i j j i ij ij ji ij L E f f f L E f f L f f f f f f εεδεδεεεεεεε=--=-=∴=∑∑ 对变分,为常数,可不管。
其中为Lagrange 乘子直接作变分可以,也可以先将[]矩阵对角化:实的:厄米的,即[]矩阵为厄米的,即[]为厄米矩阵,总可以找到Unitary 酋矩阵U 使之对角化定义新基底{}'if ,它与{if 有酋交换关系:'''''1i i j ji j j ijj ijjf U f f f U f U f f f Uf U ++-=====∑∑∑及写成矩阵元形式:这样,1[]2i i i j i j i j j i iijij i jijL f h f f f g f f f f g f f f f ε=+--∑∑∑在新基底下:''1''''11''''111111[2]11[2j j ji ij k l k l ki lj ik jlijijklk l l k ki lj ik jl ij i j ki jlijkljiij ki ij jl ki ij jl k kli iiN Ni i i j i j i j j iij E f h f U U f f g f f U U U U f f g f f U U U U f f U U UU U U U U L L f h f f f g f f f f g f f εεεεδ--------+=+--====+-∑∑∑∑∑∑∑∑且则去掉'号有:]Ni i i iijf f ε-∑现在进行变分:0L δ=0[()]i i j i j j j i i ii jiL f h f f g f f f g f f fδδε==+-++=∑∑∑共轭项式子中全体,共轭项为0又因电子相互独立,坐标不相关,因此求和中每一项须为0,即()i j i j j j i i ijh f f g f f f g f f fε+-=∑此式即为Hatree-Fock方程。
形式的写出来:()()Fi i iFh i f fh iε=其中为Hatree-Fock算子若定义算子iJ(库伦算子)及iK(交换算子)*12212*12212*212212()()(1,2)()()()()(1,2)()()()(1,2)[()()](1)(1)(1)-(1)Ni i j j ijNi i j i jjNj j ijNi i j j ijNi i j i jjFi iFiJ f x f x g f x f x dxK f x f x g f x f x dxf xg P f x f x dxJ f f g f fK f f g f fHFh h J Kh f======+∑⎰∑⎰∑⎰∑∑即则方程有形式:i iij iifHatree Fockfεεε=-称为正则方程(因[]对角化至得来)为正则分子轨道。
5.2 Hatree-Fock方程解的性质①(1)Fh为厄米算子{}{}*22122*22122(1)(1)()(1)()(1)(1)(()(1)())(1)(1)-F j j jF j j jF F F i i i iF i i i i h h f x gdx P f x h h f x gdx f x h h h f f f h f f ρεεε++++=+-=+-∴==∴=∑⎰∑⎰F 则为厄米的,应有本征函数完全集Hatree-Fock 方程,构成本征函数完全集,相应的本征值为,可看出:是由轨道决定的,h 为一个积分微分方程,对于分子体系一般是不可解的,以后我们要讨论求解HF 方程(Roothaan 的工作)②HF 算子的轨道及轨道能量 HF 算子的本征函数i f 为轨道对于一个N 电子体系,将i ε排序12εε<那么HF 算子的前N 个轨道为占据轨道,一般用,,a b c 大于N 的轨道为非占据轨道,或虚轨道,,,r s i ε称为轨道能量。
轨道总能量:[]F i i iiNi i i j i j i j j i i ijf h ff h f f fg f f f f g f f εε===+-∑∑∑∑而刚才我们已经给出了体系的能量(用密度矩阵方法)101[]2,[][][]Ni i i j i j i j j i iijNa b Na b a Nr b aE f h f f f g f f f f g f f E E a h a ab g ab ab g ba a h a ab g ab ab g ba N r h r rb g rb rb g br εεεεψε=≠≠=+-≠>=+-∴=+-⎫⎪⎪⎪⇒⎬⎪⎪⎪⎭=+-∑∑∑∑∑ 占据轨道能量:当a=b 时,上式第二项为——个占据轨道基态,单slater 行列式————b ——a 虚轨道能量:③Koopmans ’定理 概念:冻结轨道近似:加入或拿掉一个轨道上的电子,并不影响其它轨道,N 电子体系总能量为: 1[]2NNaabE a h a ab g ab ab g ba =+-∑∑,N-1电子体系总能量为:11[]2NN a ca cb cE a h a ab g ab ab g ba -≠≠≠=+-∑∑即去掉c 轨道则体系电离势为1N N c IP E E ε-=-=-证明:NE 重写N-1为部分 + 一个带(c )的部分:1111[]21[]21[]2()[]1[2NNa ca cb cNa cb cNa cb cNN Nca cN N rN aE a h a c h c ab g ab ab g ba g cb cb g bc ac g ac ac g ca Ionization Potential IP IP E E c h c ac g ac ac g ca E E E a h a r h r ab εε≠≠≠=≠≠=-≠++=++-+-+-=-=---=--=-=++∑∑∑∑∑∑从而 为:并且,体系电子亲和势可类似求出:即11]1[]21[]2[]000,0Nab NaNbNN N rac r N N r g ab ab g ba ar g ar ar g ra rb g rb rb g br E E r h r ar g ar ar g ra E E εεεε++-+-+-∴-=---=-<∴><>>∑∑∑∑一般电离能而为虚轨道,不好说。
若则电子亲和势,即,则N+1体系比N 体系更稳定。
上面两条式子就是Koopmans 定理的内容。
它将电离势与电子亲和势与轨道能量联系起来,可是实际应用中有局限性。
Koopmans 定理局限性:1. 忽略了电子重排——松弛效应2. 忽略了电子相关3. 忽略了相对论效应所以,电离势的计算,若要尽量准确的话,还需要加上对2,3的修正。
但在Hatree-Fock 方程基础上,我们只能最多对1进行修正。
文献中有两种电离势定义: 垂直电离势:即离子与分子都用分子的几何(来修正)绝热电离势:,M M +分别优化(修正,考虑松弛) ④Brillouin 定理 薛氏方程H E ψψψ∧=为H 真实,准确基态而HF 方法用单slater 行列式0ψ来近似ψ,H ∧在0ψ下有平均值000H E ψψ∧=00000001000,():NF i aaHatree Fock Hamiltonian H H HF Hamiltonian H h i H ψψεψεεε∧∧∧=∧-===∑∑其实为的本征函数其中:本征值,我们要求体系真实基态,必须包括其它形式的slater 行列式,即对HF 基态修正,我们总可以写成:00,0000000001[]rr a a r ar a r a r ra a r a r r r a aara Nb Fa a c c c c H H H H H a h r ab g rb ab g br a h r a r ψψψψψψψψψψψψψψψψψψψψεεδ∧∧∧∧∧==++=+⎛⎫ ⎪ ⎪ ⎪⎝⎭=+-===∑∑其中为HF 基态为中a 被虚轨道r 取代,为第一激发态,现在我们只考虑某一单激发态,则其对应的本征方程为HC=EC 我们现在来求Hamiltonian 矩阵:H=00000arrr aa H H H ψψψψ∧∧⎛⎫ ⎪ ⎪ ⎪⎝⎭所以矩阵中,非对角元为,则H 为:H=也即HF 基态在某种意义上“稳定的”,因其不能由考虑单激发态而得到修正。
