分数除法讲义
分数除法 讲义

( )相当于这样的2份,2/3对应的数量是()。
②甲的 相当于乙。把( )平均分为5份,把()看作单位“1”,
( )相当于这样的3份,3/5对应的数量是()。
③现价是原价的 。把( )平均分为40份,把()看作单位“1”,( )
相当于这样的3份,3/40对应的数量是()。现价比原价少的部分对应的分率是()。
④小红的书比小明少 。把( )平均分为8份,把()看作单位“1”,( )
相当于这样的7份,7/8对应的数量是()。小明的书对应的分率是()。
例2、根据已知条件用“——”线标出单位“1”的量,再写出数量关系式。
(1)白兔只数的 是黑兔的只数。(2)已经修了公路全长的 。
(3)二班植树棵数相当于一班的 。(4)今年棉花产量比去年增加 。
例9、一项工作,由甲单独做需要10天;由乙单独做需要12天.如果两人合做,几天才能完成?
课后作业
3、六年级有男生100人,女生有80人。
(1)男生人数是女生的几分之几?
(2)女生是男生的几分之几?
(3)女生是全年级学生的几分之几?
(4)男生人数比女生多几分之几?
3、某生产队挖一条长300米的水渠,第一天挖了全长的1/4,挖了多少米?还剩多少米?
2、整数的倒数小于它本身。
3、真分数的倒数大于它本身。
4、假分数的倒数小于或等于它本身。
5、1的倒数是1,0没有倒数。
积与乘数的关系:一个数(零除外)乘大于1的数,积比第一个因数大;乘小于1的数,积比第一个因数小;乘以1,积与第一个因数相等。
商的大小与除数的关系:一个数(零除外)除以小于1的数,商大于被除数;除以大于1的数,商小于被除数;除以1,商德
第三讲分数除法讲义

第三讲分数除法讲义(1)一、倒数的概念、特征以及特殊数的倒数。
1、倒数:乘积是一的两个数互为倒数。
强调:互为倒数的意义。
2、整数的倒数小于它本身。
3、真分数的倒数大于它本身。
4、假分数的倒数小于或等于它本身。
5、1的倒数是1,0没有倒数。
6、积与乘数的关系:一个数(零除外)乘大于1的数,积比第一个因数大;乘小于1的数,积比第一个因数小;乘以1,积与第一个因数相等。
7、商的大小与除数的关系:一个数(零除外)除以小于1的数,商大于被除数;除以大于1的数,商小于被除数;除以1,商等于被除数。
二、基础题1、求一个分数的倒数,只要把( )2、 的倒数是( ),( )的倒数是7,1的倒数是( ),0( )3、261时=( )分钟 ; 12.5时=( )分钟 ;453时=( )分钟 4、24等于乙数的倒数,乙数是( )。
5、( )是40的倒数,45是( )的倒数。
二、分数除法的意义分数除法的意义和法则:意义:分数除法与整数除法的意义完全相同,都是已知两个数的积与其中一个因数,求另一个因数的运算。
法则:甲数除以乙数(不为0),等于甲数乘乙数的倒数。
甲数、乙数可以是整数、小数和分数。
一个数(0除外)除以真分数,商>被除数。
一个数(0除外)除以1,商=被除数。
一个数(0除外)除以假分数(大于1),商<被除数【例1】:1)说一说下面各除法算式所表示的意义。
769÷ 251310÷ 14157÷ 10918÷2)列式计算。
①把78平均分成4份,每份是多少? ②已知一个数的32是24,求这个数? ③已知两个因数的积是98,其中的一个因数是40,求另一个因数? 【例2】比较大小。
432743()÷ 545454()÷ 237323()÷小结:整数除以分数,可以转化为乘以这个分数的倒数计算,分数除以分数,可以用被除数乘以除数的倒数计算。
【例3】一个正方体的表面积是43平方米,那么这个正方体一个面的面积是多少平方米?【例4】一辆汽车53小时行36千米,平均每小时行多少千米?四、 课堂练习1、简便运算: 611×360÷7 1÷1001÷10001 454×1353-454×3.62、光明小学六(1)班有学生45人,约占全校人数的1.5%,全校大约有学生多少人?3、一段铁丝长20米,剪成每段4/5米,可以剪成几段?4、 58X = 40 \F(2,5) X = \F(4,9) ×\F(3,8)5、154除51的商,再除以253,商是多少?6、154除以51的商,再除以253,商是多少?五、综合训练判断正误1. 35÷5 = \F(5,3) ×5 ( ) 2、4分米的15和5分米的错误!相等。
分数除法讲义

倒数与分数除法1、了解倒数、分数除法的意义教学目的2、掌握计算方法3、会运用在实际冋题中重点:计算方法及实际问题中的运用难点:实际问题中的运用教学内【知识点一】:倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1。
例如:a>b=1则a、b互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1>=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a的倒数为1;分数b的倒数是空。
a a b1真分数的倒数是假分数,真分数的倒数大于1,也大于它本、身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2用倒数解决问题、(1)用转化的方法解决倒数问题例题1: 一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小3 3 7例题2:如果aX _ = bX— = cX —,且a,b,c均不为0,把a, b,c这三个数按从大到小的顺4 5 3序排列。
(3):用假设的方法解决倒数问题1例题3:两个连续自然数的倒数差是12,求这两个自然数。
小结:解决此类问题,解可以假设其中一个自然数是a,另一个为a+1,再根据题意中的数量关系求【巩固练习二】31、3的倒数是(812、一X()2 ),0.25 和()互为倒数。
18)X 2 = 1X( )= 3 X( )= 17213. 一个自然数与它的倒数的差是21-22,这个数是多少?4 2 14.如果X X - = y X -=z X 1,且X, y,z均不为0,请按照从小到大的顺序排列这三个数。
分数除法讲义【精选】

课 题倒数与分数除法教 学 目 的1、了解倒数、分数除法的意义2、掌握计算方法3、会运用在实际问题中重 难 点重点:计算方法及实际问题中的运用 难点:实际问题中的运用教 学 内 容【知识点一】 :倒数1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。
单独一个数不能称为倒数。
(必须说清谁是谁的倒数)(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。
例如:a×b=1则a 、b 互为倒数。
2、求倒数的方法:①求分数的倒数:交换分子、分母的位置。
②求整数的倒数:整数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1×1=10没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a 的倒数为a 1 ;分数 a b的倒数是ba 。
1、真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。
假分数的倒数小于或等于1。
带分数的倒数小于1。
2、用倒数解决问题(1)用转化的方法解决倒数问题例题1:一个自然数与它的倒数的和是5.2,这个自然数是多少?小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。
整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小 例题2:如果a ×43 = b ×53 = c ×37,且a ,b ,c 均不为0,把a ,b ,c 这三个数按从大到小的顺序排列。
(3): 用假设的方法解决倒数问题 例题3:两个连续自然数的倒数差是121,求这两个自然数。
小结:解决此类问题,可以假设其中一个自然数是a ,另一个为a+1,再根据题意中的数量关系求解【巩固练习二】1、83的倒数是( ),0.25和( )互为倒数。
2、21×( )=( )×718=1×( )=3×( )=13. 一个自然数与它的倒数的差是212221,这个数是多少?4.如果x ×74 = y ×92=z ×21,且x ,y ,z 均不为0 ,请按照从小到大的顺序排列这三个数。
分数除法(一)ppt课件

目
CONTENCT
录
• 分数除法概述 • 分数除法的基本性质 • 分数除法的计算实例 • 分数除法的应用实例 • 分数的乘除混合运算
01
分数除法概述
分数除法的定义
02
01
03
分数除法是一种数学运算,通常表示为两个分数相除 。
分数除法是将一个分数除以另一个分数的结果。
例如,将一个分数2/3除以另一个分数3/4,即表示为 (2/3) ÷ (3/4)。
分数乘除混合运算的技巧和注意事项
通分
在进行分数的乘除混合运算时, 常常需要运用通分的技巧,将不 同的分母变为相同的分母,以便
于计算。
约分
在分数的乘除混合运算中,约分 也是一个常用的技巧。通过约分 ,可以简化分数的形式,从而更
方便地进行计算。
灵活运用公式
在进行分数的乘除混合运算时, 需要灵活运用各种公式,以便于
快速准确地得到结果。
THANK YOU
感谢聆听
进行运算
将分子相除,分母相乘得到结果
。例如,$\frac{3}{4}
Hale Waihona Puke \div\frac{2}{3} = \frac{3}{4} \times
\frac{3}{2}$。
03
分数除法的计算实例
简单的分数除法计算实例
题目
计算 1/2 ÷ 3/4
答案
1/2 ÷ 3/4 = 2/3
解释
首先,将除法转换为乘法,即 (1/2) × (4/3)。分子乘以一个数,分母除以同一个数,可 以得到新的分数。所以,1/2 × 4/3 = 2/3。
乘法是加法的重复
分数乘法可以看作是加法的重复,即把相同的数加起来。例如,$\frac{3}{4} \times 3 = \frac{3}{4} + \frac{3}{4} + \frac{3}{4}$。
人教版六年级数学上册 分数除法 讲义

分数除法 讲义知识点一、分数除法的意义及运算法则例1、计算(1)20÷310×45 (2)34÷38÷118 (3)(15−16)÷110(4)30÷(14+15) (5)716×45−79÷143(6)310÷0.5×23(7)(43+415)÷15÷16总结:1、除以一个不为0的数,等于乘以它的________。
这样除法问题就可以转化为乘法问题来解决。
2、带分数要转化为_______,小数要转化为_______,再找出它们的倒数。
3、除法没有分配律!乘法才有分配律。
4、注意运算顺序,先乘除,后加减,审题时看清楚。
的倒数是(),()的倒数是0.75.例2、156例3、0.125的倒数是(),3的倒数是()。
性质:○10(1)一个正数乘以一个小于1的数,结果比原来小。
例如10×34○10(2)一个正数乘以一个大于1的数,结果比原来大。
例如10×54性质:○10(1)一个正数除以一个小于1的数,结果比原来_____。
例如10÷34(2)一个正数除以一个大于1的数,结果比原来_____。
例如10÷5○104总结:“将未知的知识转化为已知的知识来解决”、“化难为易”、“化繁为简”这样的思想叫做“化归思想”。
例4、在○里填上>、<或=。
(1)95÷16○95(2)37÷9○37(3)53÷83○53(4)38÷12○38÷2(5)95÷1.5○95÷0.3(6)34÷0.7○34÷4.2知识回顾:乘法和除法互为____运算。
例5、不为0的三个数A、B、C,如果A×B=C,那么C÷B=A,C÷A=B例6、如果3×4=12,那么12÷4=3,12÷3=4分数除法、小数除法、整数除法的意义是相同的...。
人教6上分数除法讲义

章节复习考点讲义(人教版)人教版数学六年级上册章节考点精讲精练第三单元《分数除法》知识点一:倒数的认识1.倒数的意义乘积是1的两个数互为倒数。
倒数具备两个条件:一是两个数;二是乘积是1。
2.互为倒数的两个数特点如果两个数都是分数,那么两个分数的分子和分母正好颠倒了位置;如果一个是整数,则另一个分数的分子是1,分母是这个整数。
3.求一个数倒数的方法知识互联网知识导航(1)通过计算,乘积是1的两个数互为倒数。
(2)交换这个数的分子和分母的位置。
4.特殊的1的倒数是1,0没有倒数。
知识点二:分数除法的计算法则一个数除以一个不等于0的数,等于乘这个数的倒数。
知识点三:分数四则混合运算规律1. 只有乘、除法,按照从左到右的顺序依次进行计算。
2. 在没有括号的算式里,既有加、减法又有乘、除法,要先算乘、除法,再算加、减法。
3. 在一个有小括号的算式里,应该先算小括号里面的,后算小括号外面的。
知识点四:分数除法的应用题1.解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:方程法:(1)找出单位“1”,设未知量为x;(2)找出题中的等量关系式;(3)列出方程并解答;(4)检验并写出答案。
2. “已知比一个数多(少)几分之几的数是多少,求这数”的问题的解法:方程法:根据题中的等量关系:“单位‘1’的量×(1±几分之几)=已知量”或“单位‘1’的量±单位‘1’的量×几分之几=已知量”,设单位“1”的量为x,列方程解答。
3. 已知两个量的和(差),其中一个量是另一个量的几分之几,求这两个量的问题的解法:有两个量都是未知的,先把谁看作单位“1”都可以,设其中一个量为未知数x,用这个量表示另一个量,然后找出等量关系,列方程解答出一个量,再解答第二个量。
4. 利用抽象的“1”解决实际问题:工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
(完整版)分数除法讲义.doc
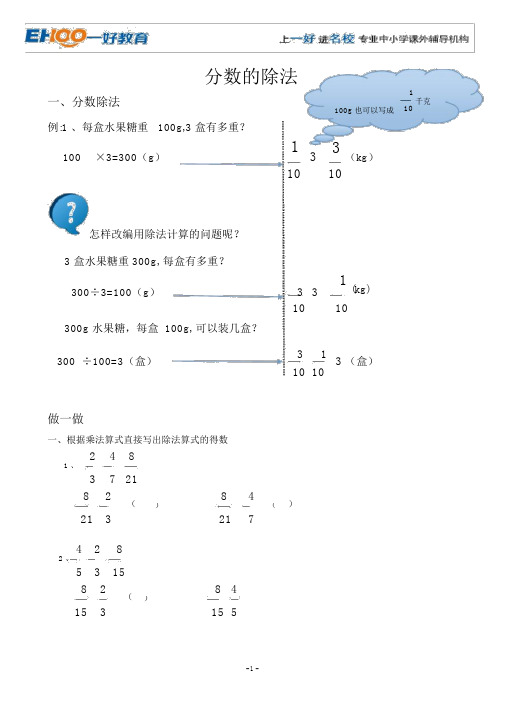
分数的除法一、分数除法例:1 、每盒水果糖重 100g,3 盒有多重? 100g 也可以写成 110千克100 ×3=300(g )133(kg )10 10怎样改编用除法计算的问题呢?3 盒水果糖重 300g, 每盒有多重?300÷3=100(g )3 3 1(kg)1010300g 水果糖,每盒 100g, 可以装几盒?300 ÷100=3(盒)3 13 (盒)10 10做一做一、根据乘法算式直接写出除法算式的得数2 4 8 1 、7 21 38 2(8 4 )21 3 )(2174 2 82 、3 15 58 2( 8 4 15 3 )5154 2、把一张纸的平均分成 2 份,每份是这张纸的几分之几?自己试着折一折,5算一算。
42 份,就是把 4 个 1把 5 平均分成5 平1 ,就是2 均分成两份, 每份就是两个5 544 25 25把4 平均分成 2 份,每份就是455的 1,也就是412524 4 15 225 如果把这张纸的4平均分成 3份,每份是这张纸的几分之几?5453根据上面的折纸实验和算式,你能发现什么规律?3、小明2小时走 2km,小红5小时走了5km。
谁走得快些?312 62小明平均每小时走: 23 怎么计算呢?画个图试试吧想:先求1小时走了多少千米,也就是求 2 的1,即21。
再求 3 个1小时走了3 2 2 3多少千米,即 2 1 3 。
22 2 1333 (km)32 22 2小红平均每小时走:5 5 5 122(km)6 12 6 512为什么写成“”答:小明走得快。
通过以上两个例子,你发现了什么?分数除法的计算法则:甲数除以乙数(0除外),等于甲数乘乙数的倒数。
做一做一、用你发现的规律计算下面各题。
9 3 2381024897 4 16 5二、直接写出得数。
1 1= 4÷12=8 3= 13=3 ÷12 7 9 ÷7 ÷4 10 14 5 5 9 35 ÷11 = 11 ÷ 21= 8 ÷6 = 10 ÷5 =三、填一填。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2、55比45多几分之几?
【巩固练习】
1、填空
千克是 千克的(),()米的 是50米。
2、找出题中的等量关系。
(1)白兔的只数为30,占总只数的 。(2)桌子的数量比椅子的数量多 。
() =()()×(1 )=()
(2)甲数正好是乙数的 。()× =()
3、六一班有男生32人,占全班总人数的 。六一班共有学生多少人?
【知识点二】:分数除法的意义及计算法则
1、分数除法的意义:
乘法:因数×因数=积除法:积÷一个因数=另一个因数
分数除法与整数除法的意义相同,表示已知两个因数的积和其中一个因数,求另一个因数的运算。
2、分数除法的计算法则:
除以一个不为0的数,等于乘这个数的倒数。
4、规律(分数除法比较大小时):
(1)、当除数大于1,商小于被除数;
3、小明家九月份电话费24元,相当于八月份的 ,八月份电话费多少元?
4、口算比赛,小明做对了 ,正好54题。小明做了多少题?
5、一个长方形的面积是 平方米,长 米,宽多少米?
4、食堂运来一批大米,已经吃去600千克,正好吃去 ,这批大米共多少千克?
5、汽车厂8月份比7月份多生产500辆,已知8月份比7月份增产 。7月份生产汽车多少辆?
(1)找出单位“1”,列等量关系式。(2)单位“1”的量未知,列方程解答。
2、一杯水喝去了80克,正好占这杯水的 ,这杯水多少克?
3、一张桌子比一把椅子贵30元,这个数目正好相当于椅子价钱的 。椅子和桌子各多少钱?
【作业】
一、填空
1、 千克大豆可以榨油 千克,1千克大豆能榨油()千克,要榨1千克油需要()千克大豆。
0没有倒数,因为任何数乘0积都是0,且0不能作分母。
非零整数a的倒数为 ;分数 的倒数是 。
1、真分数的倒数是假分数,真分数的倒数大于1,也大于它本身。假分数的倒数小于或等于1。带分数的倒数小于1。
2、用倒数解决问题
(1)用转化的方法解决倒数问题
例题1:一个自然数与它的倒数的和是5.2,这个自然数是多少?
例题3:两个连续自然数的倒数差是 ,求这两个自然数。
小结:解决此类问题,可以假设其中一个自然数是a,另一个为a+1,再根据题意中的数量关系求解
【巩固练习二】
1、 的倒数是(),0.25和()互为倒数。
2、 ×()=()× =1×()=3×()=1
3.一个自然数与它的倒数的差是21 ,这个数是多少?
4.如果x× = y× =z× ,且x,y,z均不为0,请按照从小到大的顺序排列这三个数。
(2)、判断两个数是否互为倒数的唯一标准是:两数相乘的积是否为“1”。
例如:a×b=1则a、b互为倒数。
2、求倒数的方法:
①求分数的倒数:交换分子、分母的位置。
②求整数的倒数:数分之一。
③求带分数的倒数:先化成假分数,再求倒数。
④求小数的倒数:先化成分数再求倒数。
3、1的倒数是它本身,因为1×1=1
2、9÷ 可以表示为()
A 9÷4×3 B 9×3÷4 C 9÷3×4 D 9÷3÷4
3、小红的邮票除以 与小明相等,那么小红的邮票()小明。
A多于B少于C等于D无法比较
4、12÷ 与12× 相比()
A意义相同B结果相同C结果和意义相同
【知识点三】:分数除法解决问题
(未知单位“1”的量(用除法):已知单位“1”的几分之几是多少,求单位“1”的量。)
(1)方程:根据数量关系式设未知量为X,用方程解答。
(2)算术(用除法):分率对应量÷对应分率=单位“1”的量
3、求一个数是另一个数的几分之几:就一个数÷另一个数
例:30是45的几分之几?
4、求一个数比另一个数多(少)几分之几:两个数的相差量÷单位“1”的量或:
①求多几分之几:大数÷小数– 1
②求少几分之几:1 -小数÷大数
11、一辆汽车从甲地去乙地,已经行了120千米,相当于全程的 。两地相距多少千米?
12、601班男生人数比女生多 ,女生30人,全班多少人?
13、一批水果,苹果是梨的 ,梨又是香蕉的 。苹果150千克,香蕉多少千克?
14.商店有120辆电瓶车,第一天卖出总数的 ,第二天卖出的比第一天的 多10辆。第二天卖出多少辆?
6、小兰的邮票比小军多24枚,这个数目正好是小军的 。小兰和小军各有多少枚邮票?
7、汽车厂8月份生产500辆,已知8月份比7月份增产 。7月份生产汽车多少辆?
8、美术班有男生20人,是女生的 ,女生有多少人?
9、甲铁块重 吨,相当于乙铁块的 。乙铁块重多少吨?
10、一本故事书162页,张杨今天看了 ,他明天从第几页开始看?
(2)、当除数小于1(不等于0),商大于被除数;
(3)、当除数等于1,商等于被除数。
【巩固练习】
1.计算题:
1、口算
6÷ 9÷ 32÷ ÷
÷ ÷ ÷ ÷
4、计算
÷ ÷ ( + )÷ ÷0.2×
3、求未知数X:
x=15 x÷ = x÷ =18
二.判断:
1、28除以 的商()28乘 的积。
A大于B小于C等于D无法比较
分数应用题中,两种数量相比的关键句非常多如:“是”、“比”“占”、“相当于”、“等于”。在含有上述几个字的句子中,后面的那个数量通常就作为标准量,也就是单位“1”。或看“的”、“几分之几的”前面的那几个字眼,就是单位“1”。
1、分数除法的数量关系式和分数乘法解决问题中的关系式相同:
(1)分率前是“的”:单位“1”的量×分率=分率对应量
分数除法讲义
课题
倒数与分数除法
教学目的
1、了解倒数、分数除法的意义
2、掌握计算方法
3、会运用在实际问题中
重难点
重点:计算方法及实际问题中的运用
难点:实际问题中的运用
教学内容
【知识点一】:倒数
1、倒数的意义:乘积为1的两个数互为倒数。
(1)、倒数是两个数的关系,它们互相依存,不能单独存在。单独一个数不能称为倒数。(必须说清谁是谁的倒数)
2、一个数的 是28,这个数是()。 里包含()个 。
3、把 × = 改写成两道除法算式。()()
4、在○里填上>、<或=。 ÷ ○ ÷6○ ÷ ○ ×2
二、列式计算:
① 是 的几分之几?一个数的 是45,这个数是多少?
三,应用题
1、一个人血液占体重的 。小明体内血液约4千克,他的体重约多少千克?
2.有白糖12千克,每 千克装成一包,共可以装几包?
小结:已知一个自然数与它的倒数的和,可以把这个和分成整数和纯小数(或真分数)两部分。整数部分就是这个自然数,纯小数(或真分数)部分就是这个自然数的倒数。
1、用假设的方法比较数的大小
例题2:如果a× = b× = c× ,且a,b,c均不为0,把a,b,c这三个数按从大到小的顺序排列。
(3):用假设的方法解决倒数问题
单位“1”的量=分率对应的量÷分率
1、分率前是“多或少”的意思:单位“1”的量×(1 分率)=分率对应量
单位“1”的量=分率对应量÷(1 分率)
例1、一批煤,烧去60吨,正好少去这批煤的 ,这批煤多少吨?
例2、一批煤,第一天烧去了60吨,第二天比第一天多少了 ,第二天烧了多少吨?
2、解法:(建议:最好用方程解答)
