第5节
第五节 两个重要极限

类型5: 幂指式的极限,先利用幂的有关运 算把式子变换成含有标准式,再用公式
求.
练习
3 x 2x 求 lim( ) . x 2 x
极限的常用计算方法
1.代入法
x 4 3x 8 lim 2 x 2 x x 3
0 2.多项式的 型,分子分母同时分解, 0 约掉同为无穷小的公因
第5节 两个重要极限
sin x 1. lim 1. x 0 x
sin x 观察函数 当 x 0时的变化趋势 . x
y sin x x
sin x 重要极限lim 1的使用要求: x 0 x
1、式中含有三角函数的分式; 2、分母与正玄函数的角变量相同; 3、角变量趋近于0. sin x 重要极限lim 1的推广(类型四) : x 0 x 公式 要求
x
1 2
例5
计算li m 1 x .
x 0 2 x
解 方法1 令 u = -x,因为 x 0 时 u 0,
( 所以 l i m 1 x l i m 1 u)
x 0 2 x u0
2 u
lim
u0
1
(1 u)
1 . 2 2 1 e u
x 0
2 5 x
答案: e
6
有时,所给函数在自变量的某个趋向 下,底的极限为1,指数的极限为无穷,
人们称这类极限为1 ”型未定式. “
1 重要极限lim 1 e的使用要求: x x
(1)幂指式的底是由1与一个接近于0的变量和 (2)底中的变量与指数间互为倒数.
sin x x 0 lim lim 1 ( 型) x 0 x 0 sin x x 0 sin 推广: lim lim 1(上下一致) 0 0 sin
第五节图乘法
4m C 4m
MP图(kN·m)
须注意两点:一是对于斜杆CD, 解:求解本题∆DV时,须注意两点:一是对于斜杆 ,应以杆 轴为基线计算;二是对于阶形住AC,应按EI不同分段图乘 不同分段图乘。 轴为基线计算;二是对于阶形住 ,应按 不同分段图乘。 (1)作MP图 作
A1 = 2 × 12.65 × 45 = 379.5 3
§6-5 图乘法
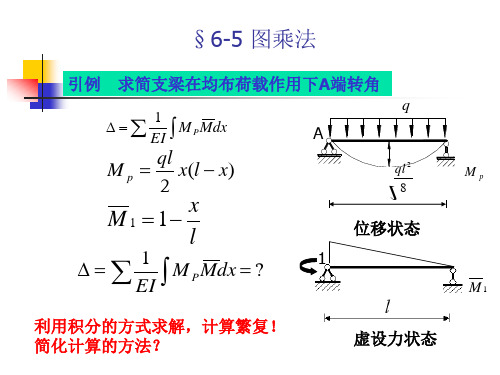
求简支梁在均布荷载作用下A端转角 引例 求简支梁在均布荷载作用下 端转角
1 ∆=∑ ∫ M P Mdx EI
q
A
ql 2 8
ql M p = x(l − x) 2
Mp
x M 1 = 1− l
1 ∆=∑ ∫ M P Mdx = ? EI
利用积分的方式求解,计算繁复! 利用积分的方式求解,计算繁复! 简化计算的方法? 简化计算的方法? 1
2.5kN/m D 2EI (12.65m) 3EI B 8m 4EI A 12m
20kN 100 A2 C A3 20 B A4 A A5
(45)
A1
D
4m C 4m
140
MP图(kN·m)
1 A2 = × 12.65 × 100 = 632.5 2
A4 =
A5 =
1 × 8 × 20 = 80 2
A q B l/2 l
ql 2 ( ) 32
ql
C l/2
并按A 作MP图,并按 1、A2、A3、A4四部 分划分,如图6-22b所示 分划分,如图 所示
∆CV 1 = ( A1 y01 + A2 y02 + A3 y03 − A4 y04 ) EI 1 = EI 1 l ql 2 l l ql 2 3 )× + ( × )× l ( × × 3 2 2 4 2 2 2
第五节 两角和与差的正弦、余弦和正切公式

数学
第五节
两角和与差的正弦、余弦和正切公式
结束
7 3 25 2. (人教 A 版教材习题改编)已知 sin(α-π)= , 则 cos 2α=________.
5
2- 3 tan 7.5° 2 3.计算: =________. 2
1-tan 7.5°
数学
第五节
两角和与差的正弦、余弦和正切公式
结束
能利用两角差的余弦公式推导出二倍角的正弦、余弦、正切公式, 了解它们的内在联系.
数学
第五节
两角和与差的正弦、余弦和正切公式
结束
(二)小题查验
1.判断正误
θ 2θ (1)cos θ=2cos -1=1-2sin 2 2
2
( √ )
(2)二倍角的正弦、余弦、正切公式的适用范围是任意角 ( × )
(3)存在角 α,使得 sin 2α=2sin α 成立 ( √ )
tan(α+β)(1-tan αtan β),且对任意角 α,β 都成立
( × )
数学
第五节
两角和与差的正弦、余弦和正切公式
结束
3 2.(人教 A 版教材例题改编)已知 sin α=- ,α 是第四象限角,则 5
π 10 cosα+4=________.
7 2
1 2 . 3.计算 cos 42°cos 18° -cos 48°cos 72° 的值为________
π 1 2 4 . ( 北师大版教材例题改编 ) 若 tan(α + β) = , tan β-4 = ,则 5 4
3 π 22 . tanα+ 的值为________
4
数学
第五节
两角和与差的正弦、余弦和正切公式
5第五节 ISM CODE解析

1.2.2 公司的安全管理目标应当包括:
1 提供船舶营运的安全做法和安全工作环境; 2 针对已认定的所有风险制定防范措施; 3 不断提高岸上及船上人员的安全管理技能,包括安全及环境保护方面的应 急准备。
1.2.3 安全管理体系(目标)应当保证:
1 符合强制性规定及规则; 2 对国际海事组织、主管机关、船级社和海运行业组织所建议的适用的规则 、指南和标准予以考虑。 35期三管考
ISM规则目标包含三层意思,ISM规则总目标、公司的安全管理目标、安全管理体系目标 ,试问安全管理体系目标是: ①提供船舶营运的安全方法及安全的工作环境 ②对所有已标识的危害建立防范措施 ③持续提高岸上及船上人员的安全管理技能,包括安全及环境保护方面的应急部署 ④符合强制性规定与规则 ⑤对有关机构、组织所建议的适用的规则、指南、及标准予以考虑。 A. ①+②+③ B. ①+④+⑤ C. ④+⑤ D. ①~⑤
武汉理工大学 WuHan University of Technology
A部分 实施
1 ቤተ መጻሕፍቲ ባይዱ则 1.1 定义
以下定义适用于本规则的A和B两部分。 1.1.1 “国际安全管理(ISM)规则”系指由国际海事组织大会通过的,并可由该组织 予以修正的“国际船舶安全营运和防止污染管理规则”。 1.1.2 “公司”系指船舶所有人,或已承担船舶所有人的船舶营运责任并在承担此种 责任时同意承担本规则规定的所有责任和义务的任何组织或法人,如管理人或光船 承租人。 1.1.3 “主管机关”系指船旗国政府。
1.1.11 “周年日”系指对应于有关文件或证书有效期届满之日的每一年中的该月该日 。
1.1.12 “公约”系指经修正的1974年国际海上人命安全公约。
新人教版八年级物理上册第四章第五节《光的色散》精品课件

课堂练习
迁移训练 2
10.冬天,在商店购买红外线烤火炉,看起来发出淡红色的光,这是因为( B ) A.红外线本身就是一种淡红色的光 B.烤火炉的电热丝在发出红外线的同时还发出少量红色的光 C.红外线中有一部分是看得见的,有一部分是看不见的 D.以上说法都错误
课堂练习
迁移训练 2 11.如图所示,将一束太阳光投射到玻璃三棱镜上,在棱镜后侧光屏上的AB范 围内观察到不同颜色的光,则( D ) A.A处应是紫光 B.只有AB之间有光 C.将照相底片放到AB范围B处的外侧,底片不会感光 D.将温度计放到AB范围A处的外侧,会看到温度上升
①紫外线可以促进人体维生素D的合成
适当照射紫外线,有助于人体合成维生素D,维生素D能 促进身体对钙的吸收,对于骨骼的生长和身体健康的许多方 面都有好处。
②紫外线消毒灭菌
紫外线消毒柜
紫外线灭菌灯
紫外线灯看起来是淡蓝色的,那是因为除了紫外线,它还 发出少量蓝光和紫光。紫外线本身是看不见的。
③紫外线能使荧光物质发光
光的色散实验
1.光的色散:白光(太阳光)经过三棱镜被分解成红、橙、黄、绿、蓝、靛、紫 等多种颜色的光。 2.白光是复合光,是由各种单色光混合而成的。
3.例如:彩虹外侧是红色,内侧是紫色
彩虹是太阳光传播中被空气中的水滴反射、折射而产生的色散现象。
小结
1.太阳光(白光)可以分解为红、橙、黄、绿、 蓝、靛、紫七种颜色的光。 2.太阳光(白光)是复合光。 3.红光、绿光、蓝光等是单色光。
把太阳光分解成七种不同的色光,按红、橙、黄、绿、蓝、靛、 紫的顺序排列起来就是太阳的可见光谱。
1.红外线
太阳光的光谱中红光外侧的不可见光叫做红外线。。
红外线
可视光线
第五节 国防概述5

第五节国防概述5一.选择题(单选):1.中央总部战区包括下列哪个战区?A.中东阿拉伯战区B.东欧战区C.西欧战区D.亚太战区答案:A2.自卫型国家代表?A.中华人民共和国B.美国C.英国D.巴西答案:A3.下面哪个国家不是一元联盟代表?A.美国B.日本C.韩国D.英国答案:D4.制定三步走战略的是?A.俄罗斯B.美国C.日本D.捷克答案:C5.珍宝岛保卫战发生在哪一年?A.1949B.1959C.1969D.1979 答案:C二.判断题:1.国防的性质是由国家的社会制度和国家的政策所决定的.(√)2.一国的社会制度不同,其国防的要求和国防也不同,因而,国防的目标也各不相同.(√)3.一个国家的经济支撑是一个国家的国防支撑.(√)4.中华人民共和国是自卫型国家.(√)5.多元体联盟是指有国家主体地位.(×)三.选择题(多选):1.联盟型国防包括?A.一元体B.两元体C.多元体D.三元体答案:AC2.不是扩张型国防的代表是?A.巴西B.法国C.德国D.美国答案:ABC3.不是自卫型国防的代表是?A.印度B.中国C.巴基斯坦D.孟买答案:ACD4.一元体联盟代表是?A.萨特阿拉伯,以色列B.美国,日本,韩国C.苏联,中国D.中国朝鲜答案:BC5.下列属于北约成员国的是?A.匈牙利B.沙特阿拉伯C.俄罗斯D.西班牙答案:AD。
高二生物(人教版)第五节细胞中的无机物课件
自由水 结合水
浸泡
增加自由水含量
降温
结合水
升温 新陈代谢 越旺盛,其___ 抗逆 性越小 比值越大,_________
自由水/结合水
缓慢 ,___ 抗逆 性越大 比值越小,新陈代谢越_____
4.烘干一粒小麦种子然后把它烧掉,
烘干时失去的是什么物质? 有机物 燃烧的是什么物质? 剩下的是什么物质? 无机盐
同种生物不同组织器官的 含水量不同。
表三:在人的不同发育期体内含水量的比较
不同发育期 幼儿 成年 老年
质量分数/%
77
52~65
51
根据上表你能得出的结论:
同种生物不同的生长发育时 期,含水量也不同 ,幼儿多 于老年。
2.水在细胞中的存在形式、定义、功能
形式
自由水
95.5%
定
义
功
能
良好溶剂、 以游离形式存在,可以 参与化学反应 自由流动 为细胞提供液体环境 运输营养物质和代谢废物 与细胞内其它物质相结 合的水 是细胞结构的组成成分
最基本元素: C 蛋白质(氨基酸) :是生命活动的主要承担者 核酸 :是遗传信息的携带者 (核苷酸) 糖类(单糖) :是生物体的主要能源物质,是细胞结构 的重要组成成分 化合物 脂质: 磷脂和胆固醇是细胞结构的重要组成成分。脂肪 是细胞中良好的储能物质。 水:是细胞结构的重要组成成分,一切生命活动都 离不开水。 无机盐: (三条略)
恢复正常 说明该种无机盐是该植物所必需的
综合练习: 种水稻时,农民把稻种放在水中浸泡一段时间,随着浸泡时间延长, 种子逐渐变甜了,萌发的种子与干燥的种子相比,自由水 /结合水的 值 ,新陈代谢速率___ 。种子变甜是由于淀粉转化 大 麦芽糖、葡萄糖 快
(化工原理)第五节 对流传热系数关联式
Nu=0.26Re0.6Pr0.33
应用范围 Re>3000
特错列征管尺距寸最狭管处外的径距do,离流应速在取(流x1-体do通)和过2每(排t2-管d0 子)中二最者狭之窄中通取小道者处。的速度。 管束排数应为10,若不是10,上述公式的计算结果应乘以下表的系数
流体无相变时的对流传热系数-12
流体有相变时的传热系数-12
二、液体的沸腾
大容积沸腾 管内沸腾
流体有相变时的传热系数-13
1.液体沸腾曲线
气化核心 泡核沸腾 或泡状沸腾 临界点 膜状沸腾
流体有相变时的传热系数-14
2.沸腾传热系数的计算
泡核沸腾传热系数的计算式
α=1.163Z(Δt)2.33 (Eq. Mostinki) 式中 Δt——壁面过热度,℃。
上式应用条件为: pc>3O00KPa, R = 0.01~0.9,q<qc 式中 Z——与操作压强及临界压强有关的参数,W/(m2•℃),其计
算式为:
流体有相变时的传热系数-16
3.影响沸腾传热的因素
(1)液体性质 (2)温度差Δt (3)操作压强 (4)加热壁面
4-5-5 壁温的估算
2.流体在换热器的管间流动
换热器内装有圆缺形挡板时,壳方流体的对流 传热系数的关联式如下:
应用范围 Re =2×1O3~10×105 特征尺寸 当量直径de 定口性温温度度的算除术μ平w均取值壁。温外,均取为液体进、出
流体无相变时的对流传热系数-13
管子为正方形排列 :
管子为正三角形排列 :
(2)高粘度的液体
应用范围 Re>10000,0.7<Pr<16700,L/d>60 特征尺寸 取为管内径di 定性温度 除μw取壁温外,均取为液体进、出
第3-5节钻扩铰锪
5、群钻显著提高了切削性能和刀具耐 用度。群钻对麻花钻主要作了三方面 的修磨: (1)在麻花钻的主后刀面上磨出两个 对称的月牙槽,形成三尖、七刃双顶 角; (2)修磨横刃,使其为原长的1/5-1/7, 并加大横刃前角; (3)对于直径大于15mm的钻头,在刀 刃的一边磨出分屑槽。
二、扩孔和铰孔 1、扩孔
2、钻头受力分析: 在各切削刃上: 轴向力Ff 径向力Fp 切向力Fc 总的扭矩: M=M0+M01+M横 轴向力: F=F0+F01+Fpe 轴向力主要由横刃产生, 扭矩主要由主刃产生。
3、麻花钻的几何角度主要有螺旋角、顶角、前角、后 角和横刃斜角。
4、麻花钻的缺点 刚度差、导向性差 横刃产生的轴向力很大 切屑与孔壁剧烈摩擦 半封闭式切削,润滑、 散热、排屑条件很差 精度低,加工质量差
切削液在较高的压力下由工件孔壁与钻杆外表 面之间的空隙进入切削区进行冷却、润滑,并将切屑经钻头的 排屑孔冲入钻杆内部向后排出。内排屑深孔钻适合加工直径 20mm以上、深径比不超过100的孔。 由于内排屑深 孔钻可以避免 切屑划伤孔壁 故加工质量较 高,精度达 IT9-7,Ra值 达3.2μm。
套料钻:中空结构,切削刃分布在四周,加工孔时它只切出
一个环形的孔,而中间留下的料芯可二次使用。适于加工直 径大于60mm的深孔及贵重材料。新型孔Βιβλιοθήκη 工刀具新型孔加工刀具完
谢谢!
毕
三、锪孔及其它孔加工刀具
用锪钻(或其他代用刀具) 加工沉头孔的方法称为锪孔。 锪孔钻有平底锪钻和锥面锪 钻。也可以用麻花钻刃磨掉 两主刃形成。
扁钻
轴向尺寸小、刚性好,结构简单、制造容易,便于采用先进 刀具材料,换刀方便,适用于数控机床,尤其在加工大直径孔 (D>38mm)时,更是比麻花钻经济。
第五节 焦耳定律
一、电动 1.电功 (1)电功的定义:电场力对电荷做的功,叫做电功. (2)电功的表达式:W=qU=UIt. 即一段电路上的电功就等于这段电路两端的电压、电 路中的电流和通电时间的乘积. (3)单位:焦耳,符号为J.
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
2.电功率 (1)定义:电流所做的功跟完成这些功所用时间的比值叫做电功 率. W (2)表达式:P= t =UI. (3)单位:瓦特,符号W. (4)物理意义:表示电流做功的快慢. P1 P2 2 (5)串联电路中:由P=I R知 R = R =…=I2,电阻越大,功率越 1 2 大,并联电路中:由P=U2/R知P1R1=P2R2=…=U2,电阻越小,功 率越大.
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
变式迁移 2.关于电功和焦耳热,下列说法错误的是( B ) A.在纯电阻电路中,计算电功可用公式W=I2Rt B.在非纯电阻电路中,计算电功可用公式W=I2Rt C.在非纯电阻电路中,计算焦耳热用Q=I2Rt D.在纯电阻电路中,计算焦耳热可以用Q=UIt=W=I2Rt
电动机启动后车灯功率减少了 ∆P=P灯1-P灯2=43.2 W 故正确选项为B.
答案:B
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
祝
您
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
第二章 恒定电流
第5节 焦耳定律 节
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
课前导读
人教版·物理 选修 人教版 物理·选修 物理 选修3-1
1.所谓电流做功,实质上是导体中的________对自由 电荷的________在做功. 2.电流在一段电路中所做的功等于这段电路________、 电路中的______、______三者的乘积,即W=________. 3.单位时间内电流所做的功叫做电功率.电流在一段电 路上做功的功率P等于________与这段电路________的乘 P ________. 积,即P=________. 4.电流通过纯电阻电路做功时,电能全部转化为 . 5.电热Q=________,热功率P=________. 6.若电路中有电动机或电解槽,电能除转化为内能外, 还转化为________或________,它们之间遵从能量守恒.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 第五节一、选择题1.(2014·长春模拟)椭圆x 2+4y 2=1的离心率为( ) A .32 B .34C .22D .23[答案] A [解析] 先将x 2+4y 2=1化为标准方程x 21+y 214=1,则a =1,b =12,c =a 2-b 2=32.离心率e =c a =32. 2.已知椭圆的一个焦点为F (0,1),离心率e =12,则椭圆的标准方程为( )A .x 22+y 2=1B .x 2+y 22=1 C .x 24+y 23=1D .y 24+x 23=1[答案] D[解析] 由已知,c =1,∵e =c a =12,∴a =2,∴b =a 2-c 2= 3.∴椭圆的标准方程为y 24+x 23=1,故选D .3.(文)(教材改编题)如果方程x 2+ky 2=2表示焦点在y 轴上的椭圆,那么实数k 的取值范围为( )A .(0,1)B .(1,2)C .(0,2)D .(0,1][答案] A[解析] 方程可化为x 22+y 22k =1,焦点在y 轴上,则有2k>2,即k <1,又k >0,∴0<k <1.(理)设0≤α<2π,若方程x 2sin α-y 2cos α=1表示焦点在y 轴上的椭圆,则α的取值范围是( )A .⎝⎛⎭⎫0,3π4∪⎝⎛⎭⎫7π4,2π B .⎣⎡⎭⎫π2,3π4C .⎝⎛⎭⎫π2,3π4D .⎝⎛⎭⎫3π4,3π2[答案] C[解析] 化为x 21sin α+y 2-1cos α=1,∴-1cos α>1sin α>0,故选C .4.中心在原点,焦点在x 轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是( )A .x 281+y 272=1B .x 281+y 29=1C .x 281+y 245=1D .x 281+y 236=1[答案] A[解析] 依题意知:2a =18,∴a =9,2c =13×2a ,∴c =3,∴b 2=a 2-c 2=81-9=72,∴椭圆方程为x 281+y 272=1. 5.设F 1,F 2是椭圆E :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 2PF 1是底角为30°的等腰三角形,则E 的离心率为( )A .12B .23C .34D .45[答案] C[解析] 设直线x =3a2与x 轴交于点M ,则∠PF 2M =60°,在Rt △PF 2M 中,PF 2=F 1F 2=2c ,F 2M =3a2-c ,故cos60°=F 2M PF 2=32a -c2c =12,解得c a =34,故离心率e =34.6.(2014·全国大纲高考)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点为F 1、F 2,离心率为33,过F 2的直线l 交C 于A 、B 两点,若△AF 1B 的周长为43,则C 的方程为( )A .x 23+y 22=1B .x 23+y 2=1C .x 212+y 28=1D .x 212+y 24=1[答案] A[解析] 本题考查了椭圆的定义,离心率的计算,根据条件可知c a =33,且4a =43,得a =3,所以c =1,b 2=2,故C 的方程为x 23+y 22=1.二、填空题7.若椭圆x 22+y 2m =1的离心率为12,则实数m =________.[答案] 32或83[解析]e 2=c 2a 2=1-b 2a 2,则1-m 2=14或1-2m =14,解得m =32或m =83. 8.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1,F 2在x 轴上,离心率为22.过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为16,那么C 的方程为________. [答案] x 216+y 28=1[解析] 本题主要考查椭圆的定义及几何性质. 依题意:4a =16,即a =4,又e =c a =22,∴c =22,∴b 2=8.∴椭圆C 的方程为x 216+y 28=1.9.已知动点P (x ,y )在椭圆x 225+y 216=1上,若A 点坐标为(3,0),|AM →|=1,且PM →·AM →=0,则|PM →|的最小值是________.[答案]3[解析] ∵PM →·AM →=0,∴AM →⊥PM →. ∴|PM →|2=|AP →|2-|AM →|2=|AP →|2-1. ∵椭圆右顶点到右焦点A 的距离最小, ∴故|AP →|min =2,∴|PM →|min = 3. 三、解答题10.已知椭圆C 1:x 24+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率.(1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B 分别在椭圆C 1和C 2上,OB →=2OA →,求直线AB 的方程. [解析] 由已知可设椭圆C 2的方程为y 2a 2+x 24=1(a >2),其离心率为32,故a 2-4a =32,则a =4, 故椭圆C 2的方程为y 216+x 24=1.(2)设A ,B 两点的坐标分别为(x A ,y A ),(x B ,y B ),由OB →=2OA →及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4,所以x 2A =41+4k 2, 由OB →=2OA →,得x 2B =161+4k 2,y 2B =16k 21+4k 2,将x 2B ,y 2B 代入y 216+x 24=1中,得4+k 21+4k 2=1, 即4+k 2=1+4k 2,解得k =±1. 故直线AB 的方程为y =x 或y =-x . 一、选择题1.已知以F 1(-2,0),F 2(2,0)为焦点的椭圆与直线x +3y +4=0有且仅有一个交点,则椭圆的长轴长为( )A .3 2B .2 6C .27D .4 2[答案] C[解析] 设椭圆方程为mx 2+ny 2=1(0<m <n ),联立方程组:⎩⎪⎨⎪⎧mx 2+ny 2=1x +3y +4=0,消去x 得:(3m +n )y 2+83my +16m -1=0,Δ=192m 2-4(16m -1)(3m +n )=0,整理得: 3m +n =16mn ,即:3n +1m =16.又c =2,焦点在x 轴上,故1m -1n=4,联立解得:⎩⎨⎧m =17n =13,故长轴长为27.2.从椭圆x 2a 2+y 2b 2=1(a >b >0)上一点P 向x 轴作垂线,垂足恰为左焦点F 1,A 是椭圆与x轴正半轴的交点,B 是椭圆与y 轴正半轴的交点,且AB ∥OP (O 是坐标原点),则该椭圆的离心率是( )A .24B .12C .22D .32[答案] C[解析] 本题考查了椭圆离心率的求法.根据x 2a 2+y 2b 2=1可得F 1(-c,0),P (-c ,b 2a ),故OP 与AB 的斜率分别是k OP =-b 2ac ,k AB=-b a ,根据OP ∥AB 得-b 2ac =-ba,即b =C .由于a 2=b 2+c 2,即a 2=2c 2,故e =c a =22.二、填空题3.(2014·安徽高考)若F 1,F 2分别是椭圆E :x 2+y 2b 2=1(0<b <1)的左、右焦点,过点F 1的直线交椭圆E 于A 、B 两点.若|AF 1|=3|F 1B |,AF 2⊥x 轴,则椭圆E 的方程为________.[答案] x 2+32y 2=1[解析] 如图,由题意,A 点横坐标为c , ∴c 2+y 2b 2=1, 又b 2+c 2=1,∴y 2=b 4,∴|AF 2|=b 2, 又∵|AF 1|=3|BF 1|,∴B 点坐标为(-53c ,-13b 2),代入椭圆方程得,⎩⎪⎨⎪⎧(-53c )2+(-13b 2)2b 2=1,b 2=1-c 2,∴⎩⎨⎧c 2=13,b 2=23方程为x 2+32y 2=1.4.(文)(2014·江西高考)设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左右焦点为F 1,F 2,过F 2作x轴的垂线与C 相交于A ,B 两点,F 1B 与y 轴相交于点D ,若AD ⊥F 1B ,则椭圆C 的离心率等于________.[答案]33[解析] 本题是椭圆综合性质的考查,∵AB ⊥x 轴,不妨设A (c ,b 2a ),B (c ,-b 2a ),又∵D 是F 1B 与y 轴的交点,可求得D (0,-b 22a)且为BF 1的中点.∵AD ⊥F 1B ,∴△F 1AB 为等腰三角形,∴|AF 1|=|AB |=2·b 2a ,∴|AF 1|+|AF 2|=2·b 2a +b 2a =3·b 2a ,由椭圆定义得3·b 2a =2a ,∴b 2a 2=23,∴c 2a 2=13,∴e =33. (理)(2014·江西高考)过点M (1,1)作斜率为-12的直线与椭圆C :x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,若M 是线段AB 的中点,则椭圆C 的离心率为________.[答案]22[解析] 由题意可设A (x 1,y 1),B (x 2,y 2),则可得⎩⎨⎧x 21a 2+y 21b2=1(a >b >0), ①x 22a 2+y22b 2=1(a >b >0).②①-②,并整理得x 1+x 2a 2(y 1+y 2)=-y 1-y 2b 2(x 1-x 2).(*)∵M 是线段AB 的中点,且过点M (1,1)的直线斜率为-12,∴x 1+x 2=2,y 1+y 2=2,k =y 1-y 2x 1-x 2=-12.∴(*)式可化为1a 2=12b2,即a 2=2b 2=2(a 2-c 2),整理得a 2=2c 2, 即c 2a 2=12.∴e =c a =22. 三、解答题5.设椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点(0,4),离心率为35.(1)求C 的方程;(2)求过点(3,0)且斜率为45的直线被C 所截线段的中点坐标.[解析] (1)将(0,4)代入C 的方程得16b2=1,∴b =4,又e =c a =35得a 2-b 2a 2=925,即1-16a 2=925,∴a =5,∴C 的方程为x 225+y 216=1.(2)过点(3,0)且斜率为45的直线方程为y =45(x -3).设直线与C 的交点为A (x 1,y 1),B (x 2,y 2), 将直线方程y =45(x -3)代入C 的方程,得x 225+(x -3)225=1,即x 2-3x -8=0, ∴AB 的中点坐标x =x 1+x 22=32,y =y 1+y 22=25(x 1+x 2-6)=-65,即中点为(23,-65). 6.(文)(2014·天津高考)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,右顶点为A ,上顶点为B .已知|AB |=32|F 1F 2|. (1)求椭圆的离心率;(2)设P 为椭圆上异于其顶点的一点,以线段PB 为直径的圆经过点F 1,经过点F 2的直线l 与该圆相切与点M ,|MF 2|=2 2.求椭圆的方程.[解析] (1)如图所示, 由椭圆的几何性质 |AB |=a 2+b 2,而|AB |=32|F 1F 2|, ∴a 2+b 2=34×4c 2=3c 2.又b 2=a 2-c 2,∴2a 2=4c 2,即e 2=12,∴e =22.(2)由(1)设椭圆方程x 22c 2+y 2c2=1.设P (x 1,y 1),B (0,c ),F 1(-c,0),F 2(c,0), ∵P 是异于顶点的点,∴x 1≠0,y 1≠0. 以PB 为直径的圆过F 1,即PF 1⊥BF 1, ∴y 1x 1+c ·c c=-1,∴y 1=-(x 1+c ). 设PB 中点D (x 12,y 1+c 2),即D 为(x 12,-x 12).由题意得|DF 2|2=|DM |2+|MF 2|2, ∵|DM |=|DB |=r ,∴|DF 2|2=(x 12-c )2+x 214,|MF 2|2=8,|DM |2=x 214+(c +x 12)2,即(x 12-c )2+x 214=8+x 214+(c +x 12)2. 整理得cx 1=-4①又P (x 1,-(x 1+c ))在椭圆上,∴x 21+2(x 1+c )2=2c 2整理得3x 21+4cx 1=0②∵x 1≠0,∴⎩⎪⎨⎪⎧3x 1+4c =0cx 1=-4,解之得c 2=3,∴所求椭圆方程为x 26+y 23=1.(理)(2014·天津高考)设椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,右顶点为A ,上顶点为B .已知|AB |=32|F 1F 2|. (1)求椭圆的离心率;(2)设P 为椭圆上异于其顶点的一点,以线段PB 为直径的圆经过点F 1,经过原点O 的直线l 与该圆相切,求直线l 的斜率.[解析] (1)设椭圆右焦点F 2的坐标为(c,0),由|AB |=32|F 1F 2|,可得a 2+b 2=3c 2,又b 2=a 2-c 2,则c 2a 2=12. 所以,椭圆的离心率e =22. (2)由(1)知a 2=2c 2,b 2=c 2,故椭圆方程为x 22c 2+y 2c 2=1. 设P (x 0,y 0),由F 1(-c,0),B (0,c ), 有F 1P →=(x 0+c ,y 0),F 1B →=(c ,c )由已知,有F 1P →·F 1B →=0,即(x 0+c )c +y 0c =0, 又c ≠0,故有x 0+y 0+c =0.①又因为点P 在椭圆上,故 x 202c 2+y 20c2=1②由①和②可得3x 20+4cx 0=0,而点P 不是椭圆的顶点,故x 0=-43c ,代入①得y 0=c 3,即点P 的坐标为(-4c 3,c3).设圆的圆心为T (x 1,y 1),则 x 1=-43c +02=-23c ,y 1=c 3+c 2=23c ,进而圆的半径r =(x 1-0)2+(y 1-c )2=53C . 设直线l 的斜率为k ,依题意,直线l 的方程为y =kx ,由l 与圆相切,可得|kx 1-y 1|k 2+1=r ,即|k(-2c3)-2c3|k2+1=53c,整理得k2-8k+1=0,解得k=4±15. 所以,直线l的斜率为4+15或4-15.。
