正方体的截面展开图
正方体的展开图.

七年级《数学》上册
正方体的十一种展开图
铅山三中 杨志香
柱 (柱,锥),有六 1.正方体是属于棱——— —— 正方形 个面,每个面都是——————
2.如果将正方体沿某些棱剪开并铺平,应
有 六 个 正方 形
小壁虎的难题:
如图:一只圆桶的下方有一只壁虎 ,上方有一只蚊子,壁虎要想尽快吃 到蚊子,应该走哪条路径?
5
第 1种
2 3 4 5
1
6 1 2 3 4
同种类型 退出
6
一、标准型(“141”)
5
第 2种
2 3 4 5 6 1 2 3 4
1
同种类型 隐藏
6
一、标准型(“141”)
5
第 3种
2 3 4 5 6 1 2 3 4
1
同种类型 隐藏
6
一、标准型(“141”)
5
第 4种
2 3 4
1
5
6
1 同种类型 隐藏
正确答案:C
A. B. C. D.
抢答题
请在下图中补上一个正方形,使它成 为一个正方体的展开图(画出三种情况)。
6 6 6 ×× × 1 2 3 ×× ×× 4 5 6 ×××
共有四种不同的选法
1、分类画出正方体的11种展开图。
(1) (2) (3) (4) (5) (6)
①
②
③
⒈
⒉
X Y PWN Z K F AHQR ESLBJD T CMG U O
第 3种
4
5
1
2
3 6
移动
恢复
三、阶梯型(“222”)
移动 恢复
1
2
3
4
移动
正方体的展开及解题规律

正方体展开图规律及解题规律一、两种展开图肯定不能拼成正方体(1)“田”字格型,只要所给的图形出现“田字格”,就不能拼成正方体。
如:(2)“4+2"型,即中间有一行(列)是连续四个小正方形,还有两个小正方形出现在同一侧,如:二、四种展开图可以能拼成正方体(1)“1+4+1”型,即中间有一行(列)是连续四个小正方形,还有两个小正方形出现在两侧,这样的展开图可以拼成正方体.如:(2)“3+3"型,即有两行(列),每行(列)3个,但不能出现“田”字格,这样的展开图可以拼成正方体。
如(3)“2+2+2”型,即有三行(列),每行(列)2个,但同样不能出现“田”字格,此型像台阶,这样的展开图可以拼成正方体。
如(4)“1+3+2"型,即有三行(列)中,中间一行(列)有3个连续的小方形,两边分别是一个小正方形和两个小正方形,不过此型有个要求,这个“1+3+2”中的“2”,即两个小正方形要求连续,不能分开,更不能出现“田字格”,这样的展开图可以拼成正方体。
如:无盖正方体展开图类型一、“1+3+1”型二、“1+2+2"型三、“2+3”型四“1+4”型正方体的截面示意图一、截面是三角形二、截面是四边形三、截面是五边形四、截面为六边形正方体的展开和折叠问题的解题规律正方体的展开和折叠问题在中考题中经常出现,多见于填空题和选择题。
这种题有利于培养学生的空间观念和实践、探索能力.本文对几种常见类型的解题规律作初步的探讨.一、判断给定的图形是否是正方体的展开图例1:将一个正方体纸盒沿棱剪开并展开,共有_______种不同形式的展开图。
解:具体有以下11种图形,1.“一·四·一" 型,中间一行4个作侧面,两边各1个分别作上下底面,•共有6种.2.“二·三·一"(或一·三·二)型,中间3个作侧面,上(或下)边2•个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共3种.3.“二·二·二"型,成阶梯状.4.“三·三"型,两行只能有1个正方形相连.二、找正方体相邻或相对的面1.从展开图找.例2水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表示。
正方体的11种展开图(描点,描线含练习题)
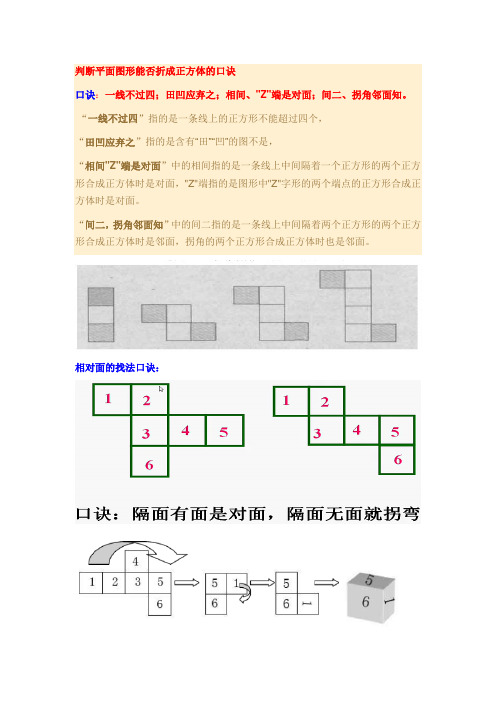
判断平面图形能否折成正方体的口诀口诀:一线不过四;田凹应弃之;相间、"Z"端是对面;间二、拐角邻面知。
“一线不过四”指的是一条线上的正方形不能超过四个,“田凹应弃之”指的是含有“田”“凹”的图不是,“相间"Z"端是对面”中的相间指的是一条线上中间隔着一个正方形的两个正方形合成正方体时是对面,"Z"端指的是图形中"Z"字形的两个端点的正方形合成正方体时是对面。
“间二,拐角邻面知”中的间二指的是一条线上中间隔着两个正方形的两个正方形合成正方体时是邻面,拐角的两个正方形合成正方体时也是邻面。
相对面的找法口诀:第18讲 图形推理-空间重构类-描点法(图形)(流畅).f4v答案:B 答案:D。
答案:A。
答案:B 答案:C答案:B。
答案:C。
【例题1】(2012年国家)左边给定的是纸盒的外表面,下面哪一项能由它所折叠而成()一本通解答:由以上性质可以可以看出,一点面和四点面为对立面,B项错误;C项中一点面与六点面构成如图相邻关系时,五点面应位于左面而右顶面(可以六点面为上面折叠),排除;二点面、三点面、四点面三面相邻,且公共顶点不变,三点面方向不对,D项错误。
注:平面图形的公共顶点和公共边折叠成多面体后仍为这三个面的公共顶点和公共边。
(通过上图D项可验证)【例题2】(2010年国家)左边给定的是纸盒的外表面,下面哪一项能由它所折叠而成()一本通解答:横线面和空白面为对立面,C、D项错误;B项中右面及上面的两条线错误,排除。
【例题3】左边给定的是纸盒的外表面,下面哪一项能由它折叠而成?一本通解答:A项三条斜线不可能交于一点,排除。
C项两条水平线不会交于一点,排除。
D项正面应为竖直线,排除。
【例题4】(2008年江苏B类)一本通解答:B。
解法一:三个空白面都不相互对立,是相邻的,B项正确。
解法二:三条对角线不会交于一点,也不会首尾相连,排除C、D两项;前表面和右表面的线段交点应该是在下方,排除A项,所以B项正确。
正方体的截面展开图

正方体的截面与展开图一、正方体的截面:
二、正方体的展开图:
第一类:中间四连方,两侧各有一个,共六种, 如下图:
第二类:中间三连方,两侧各有一、两个,共三种。
如图7、8、9
前
图1
前
图2
前
图3
前
图4 前
图5
前
图6
第三类:中间二连方,两侧各有两个,只有一种。
如图10
第四类:两排各有三个,只有一种如图11.
前
图9
前
图8
前
图7
前
图10
前
图11
如何快速识别正方体的展开图:
一:“田”字、“一”字、“7”字,“凹”字不能法。
因为正方体的每个顶点处只有3条棱,故不可能有四个面相连,所以含有“田”的图形一定不是正方体的表面展开图,同样含有“一”、“7”“凹”字的图形也不是的表面展开图。
如下图:
二、标面法:
所谓标面法就是在所给的图形上结合空间想像,标出正方体的上、下、左、右、前、后。
如果标出后的图形的这6个面既完整、又不重复,那么就是正方体的表面展开图。
否则就不是。
标面时最好选定中间的正方形为定面。
“田”字
“凹”字
“一”字
“7”字。
正方体的展开图11种怎么画

正方体的展开图11种怎么画
正方体的11种展开图如下:
确定正方体展开图的方法口诀:
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明。
四方成线两相卫,六种图形巧组合。
跃马失蹄四分开,两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
正方体的11种展开图,如图所示:
所谓”展开图“,就是将制件的表面按一定顺序而连续地摊平在一个平面上所得到的图样。
这种图样在造船、航空、机械、化工、电力、建筑、轻纺、食品等工业部门都得至l圹泛的应用,显然,展开图画得是否准确,直接关系到制件质量、生产效率、产品成本等问题。
扩展资料:
画制件表面展开图的方法,通常有计算法和图解法两种。
1、计算法就是用求立体表面积的公式算出展开图的尺寸,按尺寸画图。
计算法虽然比较准确,但是对于形状不太规则的曲面,就不便于精确计算或者计算起来显得太繁杂,因此应用这种方法受到一定的限制。
2、图解法就是用画法几何的作图原理和方法,求画制件各表面的实形,并顺序地连成片,得到制件的展开图。
这种方法在生产上广为采用。
正方体展开图和棱柱

正方体展开图
“一四一” 型
“二三一” 型
“三三”型
“二二二” 型
棱柱与棱锥
棱柱及性质
2、棱柱 (1)棱柱的定义:
有两个面互相平行,其余各面都是四边形,并且每相邻 两个四边形的公共边互相平行,这样的多面体叫做棱柱。两 个互相平行的面叫做棱柱的底面,简称底;其余各面叫做棱 柱的侧面;两个面的公共边叫棱;两侧面的公共边叫做侧棱; 两个底面所在平面的公垂线段,叫做棱柱的高。 顶点, 对角线
斜三棱柱
直四棱柱
正五棱柱
例1 下列命题正确的是
A. 有两个面平行,其余各面都是四边形的几何体叫棱柱
B. 有两个面平行,其余各面都是平行四边形的几何体叫棱柱
C. 有两个侧面是矩形的棱柱是直棱柱
D. 有两个相邻侧面垂直于底面的棱柱是直棱柱
A1 B1 C1
A B
C
例2 棱柱成为直棱柱的一个充要条件是 A. 棱柱有一条侧棱与底面的两边垂直 B. 棱柱有一个侧面与底面的一条边垂直 C. 棱柱有一个侧面是矩形,且它与底面垂直
1
A1
C1
A1
B1 B1
E1
D1 C1
C A
C B
E A B D C
2、棱柱
(3)棱柱的分类:
按底面的边数分为: 棱柱的底面可以是三角形、四边形、五边形、…… 把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
2、棱柱
(3)棱柱的分类:
按侧棱与底面的关系分为: 1) 侧棱不垂直于底的棱柱叫做斜棱柱。 2)侧棱垂直于底的棱柱叫做直棱柱。 3) 底面是正多边形的直棱柱叫做正棱柱。
正方体的11种展开图经典实用

(17)
正方体的11种展开图
(18)
正方体的11种展开图
2.如图有一正方体房间,在房间内 的一角A 处有一只小虫,它想到房 间的另一角B处去吃食物,它采取怎 样的行走路线最近?
A
B
正方体的11种展开图
变形:如图有一长方体房间,在房间 内一角A 处有一只小虫,它想到房间 的另一角B处去吃食物,它采取怎样 的行走路线最近?
(6)
正方体的11种展开图
(7)
正方体的11种展开图
(8)
正方体的11种展开图
(9)
正方体的11种展开图
(10)
正方体的11种展开图
(11)
正方体的11种展开图
(12)
正方体的11种展开图
(13)
正方体的11种展开图
(14)
正方体的11种展16)
A
B
正方体的11种展开图
这节课我们探索了...... 这节课我体验到了...... 这节课我还想......
正方体的11种展开图
正方体的11种展开图
将正方体剪开展成一个平面图形。
正方体的11种展开图
“一四一”型
正方体的11种展开图
“二三一”型
“三三”型
“二二二”型
正方体的11种展开图
判断下列图形能不能折成正方体?
(1)
正方体的11种展开图
(2)
正方体的11种展开图
(3)
正方体的11种展开图
(4)
正方体的11种展开图
(5)
正方体的11种展开图
正方体的展开图

小组合作: 利用磁力片拼出尽可能多的正方体
的展开图,并画到方格纸上。
(注意:至少有一条棱相连, 不要出现重复的哦!)
“一四一” 型
“二三一” 型
“三三”型
“二二二” 型
判断下列图形能不能折成正方体?
(1)
注意:一线不过四
判断下列图形能不能折成正方体? (2)
归纳: “凹字形”不能折成正方体
“二二二型”1种:
正方体相对的面的规律:
(1)两个小正方形中间隔着一个小正方形的 是对面,如图中A面和B面:
A
B
(2)“Z”字两端处的是对面,如下图中的A面
和B面:
A
A
B
B
作业:
1.完成课后习题。 2.探索正方体的展开图中相邻的三个面的分布
特点?归纳总结规律。
判断下列图形能不能折成正方体?
(3)
归纳: “田字形”不能折成正方体
判断下列图形能不能折成正方体?
(4)
归纳:“L形”不能折成正方体
判断下列图形能不能折成正方体?
(1)
判断下列图形能不能折成正方体?
(2)
判断下列图形能不能折成正方体?
(3)
判断下列图形能不能折成正方体?
(4)
正方体的展开图中,展开前相对的两个面分布有什么规律?
使得它们折成正方体后,对面上的数互为 倒数,则填入正方形A、B、C的三数依次是:
3. 在A、B、C内分别填上适当的数,使它们 折成正方体后,对面上的数互为相反数.
(A)0,1,-2 (B) 1,0,-2 (C)0,-2,1 (D)-2,1,0
4.(2016河北)图1和图2中所有的正方形都全等, 将图1的正方形放在图2中的①②③④某一位置, 所组成的图形不能围成正方体的位置是( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方体的截面与展开图一、正方体的截面:
二、正方体的展开图:
第一类:中间四连方,两侧各有一个,共六种, 如下图:
第二类:中间三连方,两侧各有一、两个,共三种。
如图7、8、9
前
图1
前
图2
前
图3
前
图4 前
图5
前
图6
第三类:中间二连方,两侧各有两个,只有一种。
如图10
第四类:两排各有三个,只有一种如图11.
前
图9
前
图8
前
图7
前
图10
前
图11
如何快速识别正方体的展开图:
一:“田”字、“一”字、“7”字,“凹”字不能法。
因为正方体的每个顶点处只有3条棱,故不可能有四个面相连,所以含有“田”的图形一定不是正方体的表面展开图,同样含有“一”、“7”“凹”字的图形也不是的表面展开图。
如下图:
二、标面法:
所谓标面法就是在所给的图形上结合空间想像,标出正方体的上、下、左、右、前、后。
如果标出后的图形的这6个面既完整、又不重复,那么就是正方体的表面展开图。
否则就不是。
标面时最好选定中间的正方形为定面。
“田”字
“凹”字
“一”字
“7”字。
