有限元经典算例2 正方形薄板平面应力问题的求解
有限元考试试题及答案

江西理工大学研究生考试试卷一、 简答题(共40分,每题10分)1. 论述单元划分应遵循的原则。
2. 说明形函数应满足的条件。
3. 说明四边形等参数单元中“等参数”的含义,即为什么要引入等参数单元。
4. 阐述边界元法的主要优缺点。
二、 计算题(共60分,每题20分)1. 一杆件如图3所示,杆件上方固定后,在下方受垂直向下的集中力作用,已知:杆件材料的杨氏模量2721/100.3in lbf E E ⨯==,截面积2125.5in A =,2275.3in A =,长度in L L 1221==,集中力lbf P 100=,用有限元方法求解B 点和C 点位移。
备注:(1)1 lbf (磅力,libra force ) = 4.45 N 。
(2)杨氏模量、弹性模量、Young 氏弹性模量具有相同含义(10分)2. 如图2所示,有一正方形薄板,沿对角承受压力作用,厚度t=1m ,载荷20__12__—20__13__ 学年 第___一___学期 课程名称:_____有限元及数值模拟________ 考试时间:___2012___ 年__11__月___3___日考试性质(正考、补考或其它):[ 正考 ] 考试方式(开卷、闭卷):[ 开卷 ] 试卷类别(A 、B):[ A ] 共 九 大题温 馨 提 示请考生自觉遵守考试纪律,争做文明诚信的大学生。
如有违犯考试纪律,将严格按照《江西理工大学学生违纪处分规定》(试行)处理。
学院 专业 学号 姓名 题号 一二三四五六七八九十十一十二总 分得分pyA1A2L1L2图1F=20KN/m,设泊松比µ=0,材料的弹性模量为E,试求它的应力分布。
(15分)图23. 图示结点三角形单元的124边作用有均布侧压力q,单元厚度为t,求单元的等效结点荷载。
图3一、简答题1. 答:1)合理安排单元网格的疏密分布2)为突出重要部位的单元二次划分3)划分单元的个数4)单元形状的合理性5)不同材料界面处及荷载突变点、支承点的单元划分6)曲线边界的处理,应尽可能减小几何误差7)充分利用结构及载荷的对称性,以减少计算量2. 答:形函数应满足的三个条件:a.必须能反映单元的刚体位移,就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。
平面应变有限元计算主应力计算

文章标题:深度解析平面应变有限元计算中的主应力计算目录:一、什么是平面应变有限元计算二、主应力计算的基本原理三、平面应变有限元计算中的主应力计算方法四、实际案例分析五、个人观点和总结一、什么是平面应变有限元计算平面应变有限元计算是工程学和结构分析中常用的一种数值模拟方法。
它可以用来模拟物体在受力作用下的变形和应力分布情况,有助于工程师们在设计和建造结构时更准确地预测材料的力学性能和结构的稳定性。
平面应变有限元计算通过将实际结构离散为无数个小单元,再对这些小单元进行力学分析,最终得到整个结构的应力、变形等信息。
二、主应力计算的基本原理在平面应变有限元计算中,主应力是材料中最大的应力值,它对材料的强度和变形性能具有重要影响。
主应力计算基于弹性力学理论,通过对应力张量进行分析和计算来得到主应力的数值。
在力学中,应力张量可以表示为一个3x3的矩阵,其中包括了九个分量。
利用主应力理论,可以通过对应力张量进行特征值分解,从而求得主应力的数值和方向。
这样的计算方法能够准确地描述材料中受力部分的应力分布情况,为工程设计和结构分析提供了重要的参考信息。
三、平面应变有限元计算中的主应力计算方法1. 应变离散化:需要将整个结构进行离散化处理,将其划分成无数个小单元。
每个小单元内的应变情况可以通过离散化方法进行模拟和计算。
2. 应力计算:在每个离散化的小单元中,可以根据材料的内在力学性质和受力情况,计算出应变对应的应力分布情况。
3. 主应力计算:接下来,利用特征值分解的方法,对应力张量进行分析和计算,从而得到主应力的数值和方向。
4. 结果分析:将得到的主应力的数值和分布情况进行分析和评估,对结构的稳定性和强度进行全面评定。
四、实际案例分析为了更加具体地说明平面应变有限元计算中的主应力计算方法,我们以一个实际工程案例进行分析。
假设有一座跨越河流的桥梁结构,我们需要对其进行主应力计算,以保证其在受力作用下的结构稳定性。
在对桥梁进行离散化处理后,根据受力情况和材料性质,可以计算出桥梁内部各个小单元中的应力分布情况。
有限元经典算例2正方形薄板平面应力问题的求解.docx

算例2:正方形薄板平面应力问题的求解已知图示正方形薄板, 沿其对角线承受压力作用, 设泊松比u=0,板厚t=1m ,求此薄板应力。
_v j 「-32.52]V 2-12.52 U 3-0.88V 3-3.72 U 51.76屮6_1.76 一应力:「fl「-0.881J = -20.0 (kN/m 2); \.4.40 一F 面用Pantran/Nastran 软件计算:新建一数据库文件,[File]汎 File J-New -文件名-% ne_stess_square_plate.课本第42页3.7节计算结果如下:变形:i m卜〕「-0.88] 胡 =-3.72(kN/m 2); L zx J - 3.08 _jL T xy山1IL-1.32(kN/m 2)载荷沿厚度为均匀分布,P=20kN/m 。
_1.76 1—12.52 (kN/m 2);0 一|0K|. Analysis Code —*MSC Niisiran^Analysis Type *Structurallo^ds/BCs4.施加边界条件 ------ ---1)施加HI 加约朿■: /Xution —YeatCt Object —^Displacement. Type —*Nodal»New set name • di ,山二「‘ g" — 丁]厂丁「GeometryZ 创建几何廡型 _____ 1〉创建几何点;Action-K'rcaic, Object ->Pt )int ・ Mcthcd ->XYZ ,Point I <0 0 0]f Appl^ Point * Point — [0 1000 0] i[2000 0 0]3-划分有限元网格】)建".网格冲了 土 Action —*Create* Ohjcu —»Mesh Seed, Type —''Uni Ibrm + Number of Element +,人HI 昭口心 h 「I Surface 1.2 1.3 1.4 (按住 shift 键,可tria ,连续选取三条边),八巴监P2)划分网格:Action —>Creme. Object —>Mesh> Type —*sur f ace , e |em shaped_4I i K fu.mesher Isomesh , Topology tria3 , surface -------------------------- s urface 1, 划分网格如下:2)创建曲线=Action ■+( reales Object -+Curvcj Method —>Points Option —*2 Point- Curve 1, Startinglist * curve 3,Curve2,ii ■-■ ■■ ■!'3stiirting Point Listm ': :J —edge,option ——* 3edge , Autoexecute , surface edge 1 list curve 1, surface edge 2 list k curve 2, surface edge 3 Point List —*point t > Endin,g Point List point , Ending Point Lisi ― poinl2 3,-^poim 2icurve3,・ Ending Poim Lisi —►point 〔Elements〔Add ,|OK |. |Applyb 即在面的左上两个节点处施加x 方向约束。
ANSYS机械结构设计 第5节-二维薄板平面应力分析
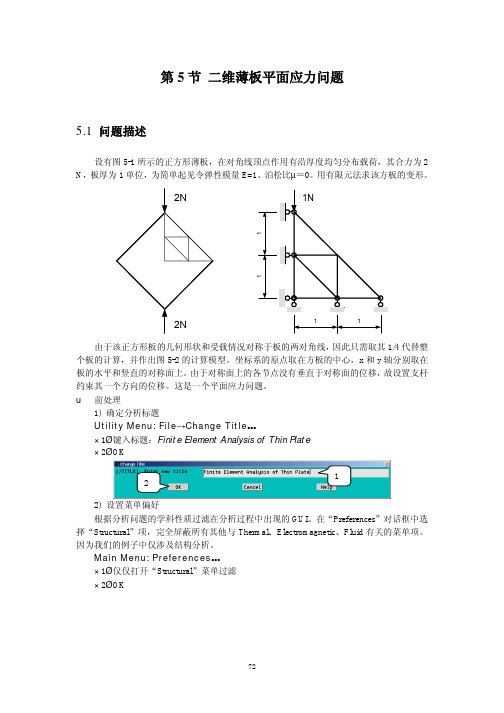
第5节 二维薄板平面应力问题5.1 问题描述设有图5-1所示的正方形薄板,在对角线顶点作用有沿厚度均匀分布载荷,其合力为2 N ,板厚为1单位,为简单起见令弹性模量E=1、泊松比µ=0。
用有限元法求该方板的变形。
由于该正方形板的几何形状和受载情况对称于板的两对角线,因此只需取其1/4代替整个板的计算,并作出图5-2的计算模型。
坐标系的原点取在方板的中心,x 和y 轴分别取在板的水平和竖直的对称面上。
由于对称面上的各节点没有垂直于对称面的位移,故设置支杆约束其一个方向的位移。
这是一个平面应力问题。
u 前处理1) 确定分析标题Utility Menu: File →Change Title …×1Ø键入标题:Finite Element Analysis of Thin Plate ×2ØOK2) 设置菜单偏好根据分析问题的学科性质过滤在分析过程中出现的GUI 。
在“Preferences ”对话框中选择“Structural ”项,完全屏蔽所有其他与Thermal 、Electromagnetic 、Fluid 有关的菜单项。
因为我们的例子中仅涉及结构分析。
Main Menu: Preferences … ×1Ø仅仅打开“Structural ”菜单过滤 ×2ØOK123) 定义单元类型:Main Menu: Preprocessor通过键盘命令直接添加单元类型,在ANSYS 窗口输入下面命令并按回车键。
ET, 1, PLANE42<回车>本例使用ANSYS 提供的PLANE42单元,该单元是ANSYS 早期开发的,已经逐步被淘汰。
如果直接通过图形用户界面(GUI)是不能找到该单元类型的。
执行了上面的命令后,我们可以通过GUI 可以检查其特性。
Main Menu: Preprocessor →Element type →Add/Edit/Delete 可以发现PLANE42单元类型已经存在。
(推荐)平面应力问题

l
yx
m yx l y
yx P xy
x
y A
fx px
x
为 l2、m2,则
y
B fy py
n
tan 2
cos(90 2 ) cos 2
m2 l2
2 x xy
(或 xy ) 2 y
22
应力主向的计算公式:
tan
1
x
(x
dx,
y)
x
(
x,
y)
x (x, x
y)
dx
1 2!
2 x (x,
x2
y)
(dx)2
1 n!
n x (
x
x,
n
y
)
(dx)n
10
略去二阶及二阶以上的微量后便得
x
(
x,
y)
x (x, x
y)
dx
同样 y 、 xy 、 yx 都一样处理,得到图示应力状
l x m yx l
m y l xy m
19
求解得:
m l
x yx
o
m yx
l y
y
2
(
x
y )
(
x
y
2 xy
)
0
yx y
x
P
A
xy
x B
px
n
n
py p
n
p x l x m yx
平面应力问题

设斜面AB上的正应力 为 n ,由投影可得:
o
xy
x
y
B P
yx
fy
y
fx
x
A
px
n lpx mpy
l x m y 2lm xy
2 2
n
py
n
N
p
设斜面AB上的切应力为 n ,由投影可得:
n lpy mpx lm( y x ) (l m ) xy
位移与形变间的关系; —— 几何方程
(3)物理学关系: 应力与应变间的关系。 —— 物理方程 (1)应力边界条件; 建立边界条件: (2)位移边界条件; (3)混合边界条件;
平衡微分方程
下面讨论物体处于平衡状态 o 时,各点应力及体力的相互 关系,并由此导出平衡微分 方程。从图所示的薄板中取 出一个微小的单元体PACB , 它在z方向的尺寸取为一个 y 单位长度,在x方向和y方向 上的长度分别为dx和dy。
x xy xz 共六个应 力分量 yx y yz zx zy z z 0
y
yx
x
xy
zx 0 zy 0
y yx
y
xy
x
x
结论:
平面应力问题只剩 下三个应力分量: 应变分量、位移分量也仅为 x、y 的函数, 与 z 无关。
在实际问题中,任何一个弹性体严 格地说都是空间物体,它所受的外力一 般都是空间力系。但是,当所考察的弹 性体的形状和受力情况具有一定特点时, 如果经过适当的简化和抽象处理,可以 简化为弹性力学平面问题,将使计算工 作量大为减少。
平面应力问题
一、平面应力问题
机械工程用有限元法学习笔记(四)
薄板弯曲问题的有限元法一、 薄板弯曲问题的基本方程什么是薄板?薄板就是指厚度t 远小于其长度、宽度的板。
1. 三个基本假设(克希霍夫假设): (1) 法线假设,εz =0,γyz =γzx =0 (2) 正应力假设,σz <<σx ,σy ,τxy (3) 小挠度假设,w<t/4根据假设,可以得到位移分量()()()()()(),,,,,,,,,,, x y z u x y z z x x y z v x y z z y x y z x y ωωωω∂⎧=-⎪∂⎪∂⎪=-⎨∂⎪⎪=⎪⎩式4-1图 1 薄板弯曲后某点B 的位移2. 应变分量{}222222x y z x z y x y ωεωεεεω⎧⎫∂-⎪⎪∂⎪⎪⎧⎫⎪⎪∂⎪⎪⎪⎪==-⎨⎬⎨⎬∂⎪⎪⎪⎪⎩⎭⎪⎪∂-⎪⎪∂∂⎪⎪⎩⎭式4-23. 曲率{}222222x y z x y x y ωχωχχχω⎧⎫∂-⎪⎪∂⎪⎪⎧⎫⎪⎪∂⎪⎪⎪⎪==-⎨⎬⎨⎬∂⎪⎪⎪⎪⎩⎭⎪⎪∂-⎪⎪∂∂⎪⎪⎩⎭式4-3 22=x x ωχ∂-∂——薄板弹性曲面在x 方向的曲率22=y yωχ∂-∂——薄板弹性曲面在y 方向的曲率2=z x yωχ∂-∂∂——薄板弹性曲面在x 方向和y 方向的扭率4. 应力分量与应变分量间的关系:{}[]{}2222222222221 11D Ez xy Ez x y Ez x y σεωωμμωωμμωμ=⎧⎫⎛⎫∂∂-+⎪⎪ ⎪-∂∂⎝⎭⎪⎪⎪⎪⎛⎫∂∂⎪⎪=-+⎨⎬ ⎪-∂∂⎝⎭⎪⎪⎪⎪∂⎪⎪--∂∂⎪⎪⎩⎭式4-4 5. 线力矩{}()2222222101012110022x y z x M Et M M y M x y ωμωμμμω⎧⎫∂-⎪⎪⎡⎤∂⎪⎪⎢⎥⎧⎫⎪⎪⎢⎥∂⎪⎪⎪⎪==-⎨⎬⎨⎬⎢⎥∂-⎪⎪⎪⎪⎢⎥-⎩⎭⎪⎪⎢⎥∂⎣⎦-⎪⎪∂∂⎪⎪⎩⎭式4-5a广义应力与广义应变之间的关系式{}[]{}D M χ= 式4-5b式中:[D]—薄板弯曲问题的弹性矩阵6. 薄板弯曲问题的基本方程(双调和方程)()32222222121Et p xx y y ωωωμ⎛⎫∂∂∂++= ⎪∂∂∂∂-⎝⎭ 式4-6()32121Et μ-——薄板弯曲刚度 二、 矩形薄板单元分析 1、矩形薄板单元图 2 矩形薄板单元2、位移函数22123456322333789101112 a a x a y a x a xy a y a x a x y a xy a y a x y a xy ω=+++++++++++ 式4-73、形状函数[]{}k i i xi xi yi yi j j xj xj yj yj k kxk xk yk y l l xl xl yl yl N N N N N N N N N N N N N q ωωθθωθθωθθωθθ=+++++++++++= 式4-8式中:i,j,k,l ——节点号N i ,N xi ,N yi ,……,N yl ——形状函数()()()()()()()()()()2211128N 111 ,,,8111 8y i i i i i xi i i iyi i i i b N i i j h l N a x a b ξξηηξξηηξηηξξηηηξξξηηξξη⎧⎫++++--⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪=-++-=⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪++-⎪⎪⎩⎭==, 式4-94、单元刚阵[][][][]S K TB D B dxdy =⎰ 式4-10式中:[]22222222222222222222 2222yi yl i xiyi yl ixi yi yl i xi N N N N x x x x N N NN B y y y y N N N N x yx yx yx y ⎡⎤∂∂∂∂⎢⎥∂∂∂∂⎢⎥⎢⎥∂∂∂∂=⎢⎥∂∂∂∂⎢⎥⎢⎥∂∂∂∂⎢⎥⎢⎥∂∂∂∂∂∂∂∂⎣⎦式4-11 5、节点力与节点位移的关系式{}[]{}F K q = 式4-12三、 三角形薄板单元分析1、三角形薄板单元当薄板具有斜交边界或曲线边界时,可采用三角形单元较好地反映边界形状。
结构力学第六章平面应力问题的有限单元法
结构力学第六章平面应力问题的有限单元法引言平面应力问题是结构力学中的重要内容之一。
为了求解这类问题,目前广泛应用的方法之一是有限元方法。
有限元方法通过将复杂的问题离散为多个简单的有限元单元,在每个单元上进行计算,最后得到整个问题的近似解。
本文将介绍平面应力问题的有限单元法的基本原理,并讨论其在结构力学中的应用。
有限单元法概述有限单元法是一种通过将连续问题离散为有限数量的简单单元,再通过求解这些单元的位移和应力来近似求解原始问题的方法。
在平面应力问题中,我们通常将结构物在平面上分割为多个有限单元,并在每个单元上进行力学分析。
有限单元法的基本思想是,先在每个单元上假设位移场的近似形式,然后将位移场的近似形式与力学原理相结合,得到每个单元上的平衡方程。
通过求解这些平衡方程,我们可以得到每个单元上的位移场和应力场。
在有限元分析中,我们通常选择线性三角形单元或矩形单元作为平面应力问题的有限单元。
这些单元通常具有简单的几何形状和计算形式,便于计算机求解。
平面应力问题的有限单元法步骤平面应力问题的有限单元法通常包括以下几个步骤:1.离散化 - 将结构物划分为多个有限单元。
在平面应力问题中,我们通常选择三角形或矩形作为单元。
2.选取近似函数 - 在每个单元上选择位移场的近似函数形式,通常选择多项式形式。
3.建立单元刚度矩阵 - 通过应用平衡方程和力学原理,建立每个单元上的刚度矩阵。
4.组装总刚度矩阵 - 将所有单元的刚度矩阵组装成总刚度矩阵。
要注意,由于每个单元的自由度不同,需要将刚度矩阵根据单元的连接关系进行组装。
5.施加边界条件 - 根据实际情况,对总刚度矩阵和载荷向量进行修正,将边界条件考虑在内。
6.求解位移场 - 通过求解线性代数方程组,得到每个单元上的位移场。
7.计算应力场 - 根据位移场,计算每个单元上的应力场。
应用案例为了进一步说明平面应力问题的有限单元法的应用,以下是一个简单的应用案例。
假设有一块矩形薄板,长为L,宽为W。
ANSYS 有限元分析 平面薄板
v1.0 可编辑可修改《有限元基础教程》作业二:平面薄板的有限元分析班级:机自101202班 姓名:韩晓峰 学号:0210一.问题描述:P Ph1mm R1mm10m m 10mm条件:上图所示为一个承受拉伸的正方形板,长度和宽度均为10mm ,厚度为h 为1mm ,中心圆的半径R 为1mm 。
已知材料属性为弹性模量E=1MPa ,泊松比为,拉伸的均布载荷q =1N/mm 2。
根据平板结构的对称性,只需分析其中的二分之一即可,简化模型如上右图所示。
二.求解过程:1 进入ANSYS程序 →ANSYS →ANSYS Product Launcher →File management →input job name: ZY2→Run2设置计算类型ANSYS Main Menu: Preferences →select Structural → OK3选择单元类型ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete →Add →selectSolid Quad 4node 42 →OK → Options… →select K3: Plane Strs w/thk →OK →Close 4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear →Elastic →Isotropic →input EX: 1e6, PRXY: → OK5定义实常数以及确定平面问题的厚度ANSYS Main Menu: Preprocessor →Real Constants …→Add/Edit/Delete →Add →Type 1→OK →Real Constant Set ,THK:1→OK →Close6生成几何模型a 生成平面方板ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Rectangle →By 2 Corners →WP X:0,WP Y:0,Width:5,Height:5→OKb 生成圆孔平面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Circle →Solid Circle→WPX=0,WPY=0,RADIUS=1→OKb 生成带孔板ANSYS Main Menu: Preprocessor →Modeling→Operate →Booleans → Subtract →Areas →点击area1→OK→点击area2→OK7 网格划分ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) Global: Set →SIZE: →OK →iMesh →Pick All → Close8 模型施加约束a 分别给左边施加x和y方向的约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement → On lines →拾取左侧边→OK →select UX,UY→ OKb 给斜边施加x方向均布载荷Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取右侧边;OK →VALUE:-10→OK9 分析计算ANSYS Main Menu: Solution →Solve →Current LS →OK→Close10 结果显示ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape…→ select Def + Undeformed →OK→Contour Plot →Nodal Solu…→select: DOF solution, Displacement vector sum, Def + Undeformed , Stress ,von Mises stress, Def +v1.0 可编辑可修改Undeformed→OK11显示整体效果Utility Menu→PlotCtrls→Style>Symmetry Expansion>Periodic/Cyclic Symmetry Expansion→1/4Dihedral Sym→OK10 退出系统ANSYS Utility Menu: File→Exit…→ Save Everything→OK三.结果分析:图1 建模、网格划分、加载图图2 变形图图3 整体应力。
平面应力问题分析实例
平面应力问题分析实例详解—带孔薄板两端承受均布载荷1 问题描述图所示为一中心带有圆孔的薄板承载示意图,薄板平均厚度为0.2mm,两端承受均布载荷P=1000Pa,求内部的应力场分布。
(薄板材料弹性模量为220GPa,泊松比为0.3)3.2 问题分析对于涉及薄板的结构问题,若只承受薄板长度和宽度方向所构成的平面上的载荷时(厚度方向无载荷),一般沿薄板厚度方向上的应力变化可不予考虑,即该问题可简化为平面应力问题(将单元关键字设置为平面应力属性)。
根据平板结构的对称性,选择整体结构的1/4建立几何模型,进行分析求解。
如果无法判断某一问题是否为平面应力问题,则需选择SOLID实体单元建立空间模型,施加载荷和相应的边界条件进行求解。
3.3 求解步骤1.定义工作文件名和工作标题1)选择Utility Menu︱File︱Change Jobname命令,出现Change Jobname对话框,在[/FILNAM]Enter new jobname文本框中输入工作文件名EXERCISE1,并将New log and error files 设置为Yes,如图3.2所示,单击OK按钮关闭该对话框。
2)选择Utility Menu︱File︱Change Title命令,出现Change Title对话框,在[/TITLE]Enter new title 文本框中输入ANALYSIS OF PLATE STRESS WITH SMALL CIRCLE,如图3.3所示,单击OK按钮关闭该对话框。
2.定义单元类型1)选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令,出现Element Types 对话框,单击Add按钮,出现Library of Element Types对话框。
在Library of Element Types列表框中选择Solid,8node 82,在Element type reference number文本框中输入1,如图3.4所示,单击OK 按钮关闭该对话框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算例2: 正方形薄板平面应力问题的求解
已知图示正方形薄板,沿其对角线承受压力作用,载荷沿厚度为均匀分布,P=20kN/m 。
设泊松比u=0,板厚t=1m ,求此薄板应力。
课本第42页3.7节计算结果如下: 变形:
⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣
⎡76.176.172.388.052.1252.32653321u u v u v v 应力:
)/(40.40.2088.02
1
m kN xy y x ⎥
⎥⎥⎦⎤
⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡τσσ; )/(052.1276.12
2
m kN xy y x ⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡-=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡τσσ; )/(08.372.388.023
m kN xy y x ⎥⎥⎥⎦⎤
⎢⎢⎢⎣⎡--=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡τσσ; )/(32.172.3024
m kN xy y x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡τσσ
下面用Pantran/Nastran 软件计算:
Plane_stess_square_plate,
[2000 0 0][0 1000 0]
Curve2,
23, curve3, 3
1
edge,option3edge,Auto execute,surface edge 1 list curve 1,surface edge 2 list curve 2,surface edge 3 list curve 3,
2,Surface 1.2 1.3 1.4(按住shift键,可连续选取三条边),
surface,elem shape tria,mesher Isomesh,Topology tria3,surface surface 1,
划分网格如下:
New set name d1,<0., ,>,
2,3,
即在面的左上两个节点处施加x方向约束。
同理,New set name d2,< , 0.,>,
Node5,6,
即在面的右下两个节点处施加y方向约束。
New set name d3,< 0, 0.,>,
Node1,
即在面的左下一个节点处施加x、y两方向约束。
<0., -10000., 0.>,
3,即在节点1处施加10kN的集中力;
施加了边界条件的图形如下:
m,
1,
2D,2D Solid,
plane strain,
m:m,
surface 1,
此时,Patran会产生一个bdf文件。
运行Nastran,打开Plane_stess_square_plate.bdf 文件,Nastran开始计算,几秒钟后会有“滴”一声,计算完毕,产生一个Plane_stess_square_plate.xdb文件。
Plane_stess_square_plate.xdb,
1)显示节点位移值:Action creat,object Marker,Method Vector,Select Result Cases Default A2:Static Subcase; Select Vector Result Displacements,translational,
show as component xx、yy,
教材计算结果:⎥⎥⎥⎥⎥⎥
⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣
⎡E E E E E E u u v u v v /76.1/76.1/72.3/88.0/52.12/52.32653321
2)显示单元应力值:Action Create ,Object Marker ,Method Tensor ;Select Result
Cases Default,A2:Static Subcase; Select Tensor Result Stresses Tensor, show as component xx 、yy 、xy; 点图标(Target Entities ),Target Entity Elements ,Select Elements
Elm1:4,Apply 。
显示截面各单元的三个方向的应力如下图:
所得计算结果与理论解相同。
