第6章 均匀平面波的反射和透射
合集下载
电磁场与电磁波期末复习知识点归纳
哈密顿算子：矢量微分算子（ Hamilton、nabla、del ）
ex
x
ey
y
ez
z
★ 标量场的梯度
gradu u u xˆ u yˆ u zˆ ( xˆ yˆ zˆ)u x y z x y z
★ 矢量场的散度计算公式：
divA＝ • A Ax Ay Az x y z
1
2=∞ nˆ • D1 s
nˆ E1 0 nˆ B1 0
nˆ H1 Js
2、理想介质表面上 的边界条件
1=0
2=0
nˆ • (D1 D2) 0 nˆ (E1 E2 ) 0
nˆ B1 B2 0
nˆ H1 H2 0
第三章 静态电磁场及其边值问题的解
静电场中: E 0
圆柱坐标和球坐标的公式了解:
Bx By Bz
圆柱坐标系中的体积微元: dV=(d)(d)(dz)= d d dz
分析的问题具有圆柱对称性时可表示为：dV=2ddz
球坐标系中的体积微元: dV=(rsind)(rd)(dr)
分析的问题具有球对称性 时可表示为:
=r2sindrdd dV=4r2dr
★ 标量场的等值面方程 u x, y, z 常数C
程的解都是唯一的。这就是边值问题的唯一性定理
◇ 唯一性定理的意义：是间接求解边值问题的理论依据。
● 镜像法求解电位问题的理论依据是“唯一性定理”。
点电荷对无限大接地导体平面的镜像
z
r1
P
q h
r r2 介质
x
h
介质
q
点电荷对接地导体球面的镜像。
P
r
a
r2
o θ q
d
’d
第6章--2 斜入射a48页PPT
思路：入射场
叠加
反射场
合成场
a)垂直极化和平行极化
Ei
Hi
① 1,1
Sˆ i i r
y
②
Er
Sˆ r
Hr
x
Ei
Er
Hr
Hi
① 1,1
Sˆ i i r
Sˆ r
y ②
x
z
z
(a) 垂直极化波
（b）平行极化波
图6.2-2 两种极化波对理想导体平面的斜入射
➢任意极化的平面波都可以分解成垂直极化波和平行极化波的合成；
kx4, kz3
2＝20.4m
k5
k kx2kz25＝ 2
sˆk kxˆ45 zˆ3xˆ5 4zˆ5 3
co ss ˆz ˆ3, arc 0 .6 t a 5.n 1 33
5
电磁场
第6章 平面电磁波的反射与折射
（b）∵ sˆH0 即 (x ˆ4z ˆ3)(x ˆAy ˆ26z ˆ4)0 55
∴ A=3
电磁场
第6章 平面电磁波的反射与折射
1. 重要概念
y 介质2 介质1
z
k E
∥
x 分界面
Ei 入射角i
E⊥ 入射面 入射方向
斜入射: 电磁波的入射方向与分界面的法线有一定夹角的 入射方式。
入射面：均匀平面波的传播方向与分界面法线所构成的平面。
电磁场
第6章 平面电磁波的反射与折射
反射角：反射波
的传播方向与分界
面法线的夹角。
分界面
x
入射面
入射角：入射波
的传播方向与分界 面法线的夹角。
r i O
折射角：透射波
的传播方向与分界 面法线的夹角。
叠加
反射场
合成场
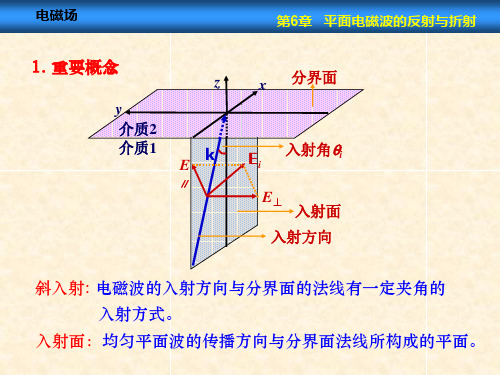
a)垂直极化和平行极化
Ei
Hi
① 1,1
Sˆ i i r
y
②
Er
Sˆ r
Hr
x
Ei
Er
Hr
Hi
① 1,1
Sˆ i i r
Sˆ r
y ②
x
z
z
(a) 垂直极化波
（b）平行极化波
图6.2-2 两种极化波对理想导体平面的斜入射
➢任意极化的平面波都可以分解成垂直极化波和平行极化波的合成；
kx4, kz3
2＝20.4m
k5
k kx2kz25＝ 2
sˆk kxˆ45 zˆ3xˆ5 4zˆ5 3
co ss ˆz ˆ3, arc 0 .6 t a 5.n 1 33
5
电磁场
第6章 平面电磁波的反射与折射
（b）∵ sˆH0 即 (x ˆ4z ˆ3)(x ˆAy ˆ26z ˆ4)0 55
∴ A=3
电磁场
第6章 平面电磁波的反射与折射
1. 重要概念
y 介质2 介质1
z
k E
∥
x 分界面
Ei 入射角i
E⊥ 入射面 入射方向
斜入射: 电磁波的入射方向与分界面的法线有一定夹角的 入射方式。
入射面：均匀平面波的传播方向与分界面法线所构成的平面。
电磁场
第6章 平面电磁波的反射与折射
反射角：反射波
的传播方向与分界
面法线的夹角。
分界面
x
入射面
入射角：入射波
的传播方向与分界 面法线的夹角。
r i O
折射角：透射波
的传播方向与分界 面法线的夹角。
第六章平面电磁波
1
2
1
二、导电媒质中平面电磁波的传播特性
1、不良导体主要参数（不能近似，计算复杂）
2、电介质主要参数（如聚四氟乙烯、聚苯乙烯、石英等）
表明：相移常数和波阻抗近似与理想电介质相同，衰减常数与 频率无关，正比于电导率。因此均匀平面电磁波在低损耗质中 的传播性，除了由微弱的损耗引起的振幅衰减外，与理想媒质 中的传播特性几乎相同。 3、良导体主要参数
表明：任一时刻电场能量密度和磁场能量密度相等，各为总电磁能量一半。 9、电磁能量平均值：
10、能量传播速度： 表明：均匀平面电磁波的能量传播速度等于相速。
z
P161 例6-1 略 补充例题：
• 6-2
P203作业2009.4.28
§6.2 导电媒质中的平面电磁波
一、导电媒质中平面电磁波的传播特性
方程的实际解：(由于无界媒质中不存在反射波)
由于：
二、均匀平面波的传播特性
可得：
振幅
时间相位
空间相位
初相
相位，代表场 的波动状态
上边两式表明：正弦均匀平面电磁波的电场和磁场在空间上互 相垂直，在时间上是同相的，它们的振幅之间有一定的比值，此比 值取决于煤质的介电常数和磁导率。
Ex
z Hy
图 6-3 理想介质中均匀平面电磁波的 上图表示 t = 0 时刻，电场及磁
4、坡印廷矢量的瞬时值
v
v
v
S(z,t) E(z,t) H (z,t)
evz
1 2
Em2
c
e2 az [cos
cos(2t
2
z
20
)]
5、复坡印廷矢量
v S
1 2
v E
v H*
均匀平面波的反射和透射matlab -回复
均匀平面波的反射和透射matlab -回复均匀平面波的反射和透射(matlab)引言：均匀平面波的反射和透射是电磁波传播中的基本现象之一。
通过研究波在边界上的反射和透射行为，我们可以更好地理解电磁波的传播规律和性质。
在本文中，我们将使用MATLAB编程来模拟均匀平面波的反射和透射现象，并详细介绍每一步的操作。
第一步：定义均匀平面波首先，我们需要定义一个均匀平面波的初始状态。
假设我们有一个平面波在z轴上传播，其电场分量Ez(x, y, t)可以由下述公式表示：Ez(x, y, t) = E0 * exp(j*(kx*x + ky*y - ωt))其中，E0表示电场强度的振幅，kx和ky分别表示波矢在x和y方向上的分量，ω表示角频率，t表示时间。
我们可以在MATLAB中定义这个函数，并设定合适的参数。
例如：MATLABE0 = 1; 设置电场强度的振幅kx = 2*pi; 设置波矢在x方向上的分量ky = 3*pi; 设置波矢在y方向上的分量omega = 10; 设置角频率t = 0; 设置初始时间定义均匀平面波函数Ez = (x, y) E0 * exp(1j * (kx*x + ky*y - omega*t));第二步：绘制均匀平面波的图像在前面的步骤中，我们定义了一个函数Ez(x, y)，用来描述均匀平面波在空间中的电场分布情况。
为了更直观地理解该函数的特性，我们可以使用MATLAB绘制二维图像。
MATLAB[X, Y] = meshgrid(-10:0.1:10); 定义绘制图像所需的坐标点Z = angle(Ez(X, Y)); 计算相位，并将其作为图像的颜色映射绘制二维图像figure;imagesc(X(1,:), Y(:,1), Z);xlabel('x');ylabel('y');colorbar;运行以上代码后，我们将得到一个二维图像，其中不同位置的颜色表示该位置上电场分量的相位。
第六章-平面波详解
E exEx ey Ey
两个分量可以表示成为
Ex
E e jkz jx xm
Ey
E e jkz jy ym
第六章 平面波
合成场矢量E可以写为
E ex Exme jkz jx ey Eyme jkz jy
瞬时值表达式分别为
Ex Exm cos(t kz x ) Ey Eym cos(t kz y ) E ex Exm cos(t kz x ) ey Eym cos(t kz y )
E2
1 4
E02e2az
第六章 平面波
平均磁能密度：
wav,m
1 4
H
2
1 4
E02
2
f
e2az
1 4
E02
e2
az
1 ( )2
总的平均能量密度：
wav
wav,e
wav,m
1 4
E02e2
z
1 4
E02e2
z
1 ( )2
1 4
E E
Ex2
E
2 y
Em
合成场矢量E与x轴正方向的夹角α为
arctan
Ey Ex
arctan
sin(t cos(t
x x
) )
(t
x
)
圆极化波有左旋和右旋之分，规定如下：
将大拇指指向电磁波的传播方向，其余四指指向电
第六章 平面波
场矢量E矢端的旋转方向，若符合右手螺旋关系，则 称之为右旋圆极化波；
谢处方《电磁场与电磁波》(第4版)章节习题-第6章 均匀平面波的反射与透射【圣才出品】
第6章 均匀平面波的反射与透射一、判断题电磁波垂直入射至两种媒质分界面时，反射系数与透射系数之间的关系为ρτ1＋＝。
（ ）ρτ【答案】√二、填空题电磁波从理想介质1垂直向理想介质2入射，介质1和2的本征阻抗分别为30Ω和70Ω，则分界面处的反射系数Γ和透射系数τ分别是_______，_______。
【答案】0.4；1.4三、简答题1．简述平面电磁波在媒质分界面处的反射现象和折射现象满足的斯耐尔（Snell ）定律；并具体说明什么条件下发生全反射现象，什么是临界角，给出临界角的计算公式。
答：（1）斯耐尔（Snell ）定律：①反射线和折射线都在入射面内；②反射角等于入射角，即；r i θθ=③折射角的正弦值与入射角的正弦值之比等于入射波所在的媒质的折射率与折射波所在媒质的折射率之比，即，式中sin sin ii n n ττθθ=n =（2）全反射现象：①理想导体全反射。
在电磁波入射到理想导体表面时，由理想导体表面切向电场为零的条件，反射系数为±1，称为理想导体全反射现象；②理想介质全反射。
当电磁波由光密介质入射到光疏介质时，由于，根据斯耐12n n >尔定律有。
当入射角增加到某一个角度时，折射角就可能等于。
因此，i τθθ>i θπ2c θ<τθπ2在时，就没有向介质2内传播的电磁波存在，即发生全反射现象。
c θθ>能使的入射角称为临界角，有：π2τθ=c θ21sin c n n θ==2．什么是电磁波在媒质分界面的全反射现象和全折射现象？什么是临界角和布儒斯特角？一个任意极化波由空气斜入射到一介质界面，以什么角度入射才能使反射波为线极化波？说明原因。
答：（1）当电磁波由光密介质入射到光疏介质时，由于，根据斯耐尔定律有12n n >。
当入射角增加到某一个角度时，折射角就可能等于。
因此，在i τθθ>i θπ2C θ＜τθπ2时，就没有向介质2内传播的电磁波存在，即发生全反射现象。
电磁场与电磁波(第4版)第6章部分习题参考解答
G
G E(z)
G
=
eGx100e− j(β z+90D )
+
G ey
200e− jβ z
由 ∇ × E = − jωμ0H 得
G H
(z)
=
−
1 jωμ0
∇×
G E(z)
=
−
1 jωμ0
⎡ ⎢
G ex
⎢∂
⎢ ⎢
∂x
G ey ∂ ∂y
G ez ∂ ∂zຫໍສະໝຸດ ⎤ ⎥ ⎥ ⎥ ⎥=
−
1 jωμ0
G (−ex
∂Ey ∂z
G (1) 电场 E = 0 的位置；(2) 聚苯乙烯中 Emax 和 Hmax 的比值。
解：(1)
令
z
'
=
z
−
0.82
，设电场振动方向为
G ex
，则在聚苯乙烯中的电场为
G E1 ( z
')
=
G Ei
(z
')
+
G Er
(z
')
=
G −ex
j2Eim
sin
β
z
'
G 故 E1(z ') = 0 的位置为 β z ' = −nπ, (n = 0,1, 2,")
G ex
G × Ei (x)
G = ez
1
− j2 πx
e3
12π
A/m
G
G
(2) 反射波电场 Er 和磁场 Hr 的复矢量分别为
G Er (x) =
G
j2 πx
−ey10e 3
G V/m ， Hr (x)
电磁场与电磁波-第六章-均匀平面波的反射和透射
(
z)
z 0
Er (z) (ex jey )Eme
jz
0
所以反射波是沿－z方向传播的左旋圆极化波
电磁场与电磁波
第6章 均匀平面波的反射与透射
16
（2）在z<0区域的总电场强度
E1(z,
Re
Re
t()ex RejeyE)ie(zj)zE(r(ezx)
(ex
je
y
)
j2 sin
1= 2= 0
则
1 j1 j 11
2 j2 j 22
1c 1
1 1
, 2c
2
2 2
2 1 , 22
2 1
2 1
讨论
x
介质1：
1, 1
Ei
ki
Hi
kr
Er Hr
介质2：
2, 2
Et
kt
Ht
y
z
z=0
当η2>η1时，Γ> 0，反射波电场与入射波电场同相
当η2<η1时，Γ< 0，反射波电场与入射波电场反相
ex
Eim
(e
j1z
e
) j1z
H1(z) Hi (z) Hr (z) ey
媒质2中的透射波：
E2
(z)
Et
(z)
ex
Eime
j2 z
Eim
1
(e j1z
e j1z )
H2(z)
Ht
(z)
ey
Eim 2
e
j2 z
电磁场与电磁波
第6章 均匀平面波的反射与透射
20
合成波的特点
E1(z) ex Eim (e j1z e ) j1z ex Eim (1 )e j1z (e j1z e j1z ) ex Eim (1 )e j1z j2 sin 1z
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：z > 0 区域的本征阻抗 x
1 , 1 , 1 0
Er
Ei
媒质1
2 r 2 120π 2 0 60π Ω 2 r2 2
透射系数
2 , 2 , 2 0
Et
媒质2
22 2 60π 0.667 1 2 120π 60π
2 2 （4） 1.12 1 2
故
j 2 z E2 ( z ) ex Etm e ex Eim e j 2 z
ex 1.12 2.4e j10.54 z ex 2.68e j10.54 z
E2 ( z, t ) ex 2.68cos(5 108 t 10.54 z )
电磁场理论
第6章 均匀平面波的反射与透射
57
例 6.3.1 一圆极化波以入射角θi＝π/ 3 从媒质1（参数为μ=
μ0、ε＝4ε0 ）斜入射至空气。试求临界角，并指出此时反射波
是什么极化？ 解：临界角为
0 2 c arcsin arcsin 4 0 1 π 6
kr H r Hi ki
y
Hale Waihona Puke Ht ktz
电磁场理论
第6章 均匀平面波的反射与透射
24
相位常数
故
3π 109 2 2 2 0 0 r 2 2 20π rad/m 8 3 10 E2 ex E2m cos(t 2 z ) ex Eim cos(t 2 z ) ex 0.667 10 cos(3π 109 t 20πz ) ex 6.67 cos(3π 109 t 20πz ) V/m
r2=10、
μr2 = 4、σ2= 0 。角频率ω＝5×108 rad /s 的均匀平面波
从媒质1垂直入射到分界面上，设入射波是沿 x 轴方向的线极化波， 在t＝0、z＝0 时，入射波电场的振幅为2.4 V/m 。求： (1) β1和β2 ； (2) 反射系数Г1 和Г2 ； (3) 1区的电场 E1 ( z, t ) ； (4) 2区的电场 E2 ( z, t ) 。 解:（1） 1 11 0 0
22
电磁能流密度 媒质1中沿 z 方向传播的平均功率密度 * 1 1 2 Siav Re Ei H i ez Eim 2 2
1
* 1 1 2 S rav Re Er H r ez 2 Eim 2 21 2 * 1 E im 2 S1av Re E H e (1 ) 1 1 z 2 2
2
2 4 0 r2 0 75.9π Ω 2 r2 10
2 1 75.9 60 0.117 2 1 60 75.9
（3） 1区的电场
E1 ( z ) Ei ( z ) Er ( z ) ex Eim (e j1z e j1z ) ex Eim [(1 )e j1z j2 sin( 1 z )] ex 2.4[1.117e j3.33 z j0.234sin(3.33 z )]
0
(3) 理想导体表面电流密度为
J S e z H1
z 0
200 jπ / 2 400 ex e ey ex j0.53 ey 1.06
0
0
电磁场理论
第6章 均匀平面波的反射与透射
21
例6.1.2
在自由空间，一均匀平面波垂直入射到半无限大的
电磁场理论
第6章 均匀平面波的反射与透射
65
例6.4.1 当垂直极化的平面波以角度i 由空气向无限大的理想 导电平面投射时，若入射波电场振幅为Eim ，试求理想导电平面 上的表面电流密度及空气中的能流密度的平均值。 解 令理想导电平面为 z = 0 平 面，如图所示。那么，表面电流 J S 为
Hi Ei Er
时的临界角θc ；（2）若入射角θi = θb ，则波全部透射
入空气。上述三种介质的θi =？ 解： 介质 水 玻璃 聚苯乙烯 临界角 c arcsin( 2 / 1 ) 布儒斯特角
b arc tan( 2 / 1 )
6.34 18.43
32
6.38 19.47 38.68
1
2 1
2 2
式中 1 0 , 2
又因为2区的波长 2
0 0 6 r r
r 0 r
1 2 0 3
r 1 r 9
r r 18
r r 36
2
电磁场理论
第6章 均匀平面波的反射与透射
故
imax arcsin( n n )
2 1 2 2
n2
i
t 1 1
n1
r1
电磁场理论
第6章 均匀平面波的反射与透射
61
例6.3.3 一平面波从介质1 斜入射到介质与空气的分界面，试 计算：（1）当介质1分别为水εr ＝81、玻璃εr ＝9 和聚苯乙烯ε
r ＝1.56
1 1 j z H r ( z ) (ez Er ) (ex 200e ey 100e j z e jπ / 2 )
0
0
电磁场理论
第6章 均匀平面波的反射与透射
14
在区域 z < 0 的合成波电场和磁场分别为
jπ / 2 E1 Ei Er ex j200e sin( z ) ey j400sin( z ) 1 H1 H i H r [ex 400 cos( z ) ey 200e jπ / 2 cos( z )]
电磁场理论
23 第6章 均匀平面波的反射与透射 例6.1.3 入射波电场 Ei ex 100 cos(3π109 t 10πz ) V/m ，从空
气（z < 0）中正入射到 z = 0 的平面边界面上。在z > 0区域中，
μr=1 、εr = 4 。求区域 z > 0的电场和磁场 。
电磁场理论
第6章 均匀平面波的反射与透射
27
或
j3.33 z E1 ( z ) Ei ( z ) Er ( z ) ex 2.4e ex 0.281e j3.33 z jt E1 ( z, t ) Re E ( z )e 1 8 ex 2.4 cos(5 10 t 3.33z ) ex 0.281cos(5 108 t 3.33z )
J S en H e z H
00
i r
0
Hr
x
z= 0
已知磁场的 x 分量为
z
Eim H x ex 2 cos i cos( k1 z cos i )e jk1 x sin i
求得
2 E im J S ey cos i e jk1 x sin i
1
0
电磁场理论
第6章 均匀平面波的反射与透射
66
能流密度的平均值 * * * 1 1 Sav Re( E H ) Re[ E y ( H x H z )] 2 2 已知垂直极化平面波的各分量分别为
E y e y j2 Eim sin( k1 z cos i )e jk1 x sin i Eim H x ex 2 cos i cos( k1 z cos i )e jk1 x sin i
1
入射波平均功率 密度减去反射波 平均功率密度
媒质2中的平均功率密度
2 * 1 Eim 2 S 2av Re E H e 2 z 2 2 2 2 1 2 2 1 (1 )(1 ) 由 2
S1av S 2av
可见入射角θi＝π/ 3大于临界角θc＝π/ 6 ，此时发生全反射。 入射的圆极化波可以分解成平行极化与垂直极化的两个线极 化波，虽然两个线极化波的反射系数的大小此时都为1，但它们的 相位差不等于±π/ 2，因此反射波是椭圆极化波。
电磁场理论
第6章 均匀平面波的反射与透射
58
例6.3.2 下图为光纤的剖面示意图，如果要求光波从空气进入 光纤芯线后，在芯线和包层的分界面上发生全反射，从一端传至 另一端，确定入射角的最大值。 解：在芯线和包层的分界面上发生全反射的条件为
无耗介质平面上，已知自由空间中，合成波的驻波比为3，介质内 传输波的波长是自由空间波长的1/6，且分界面上为驻波电场的最 小点。求介质的相对磁导率和相对介电常数。
1 解：因为驻波比 S 3 2 1 1 由于界面上是驻波电场的最小点，故 2 而反射系数 2 1
j z jπ/2 Ei ex 100e e ey 200e j z
则
1 1 j z H i ( z ) ez Ei (ex 200e e y 100e j z e jπ/2 )
0
0
电磁场理论
第6章 均匀平面波的反射与透射
1 c arcsin 2 / 1 arcsin(n2 / n1 )
由于 1
sin 1 sin c n2 / n1
n2 cos t sin c n1
r2
2
t
sin 1 sin( t ) cos t 2
2 2 2 2 sin n sin n 1 cos n 1 ( n / n ) n n 所以 i 1 t 1 t 1 2 1 1 2
1 , 1 , 1 0
Er
Ei
媒质1
2 r 2 120π 2 0 60π Ω 2 r2 2
透射系数
2 , 2 , 2 0
Et
媒质2
22 2 60π 0.667 1 2 120π 60π
2 2 （4） 1.12 1 2
故
j 2 z E2 ( z ) ex Etm e ex Eim e j 2 z
ex 1.12 2.4e j10.54 z ex 2.68e j10.54 z
E2 ( z, t ) ex 2.68cos(5 108 t 10.54 z )
电磁场理论
第6章 均匀平面波的反射与透射
57
例 6.3.1 一圆极化波以入射角θi＝π/ 3 从媒质1（参数为μ=
μ0、ε＝4ε0 ）斜入射至空气。试求临界角，并指出此时反射波
是什么极化？ 解：临界角为
0 2 c arcsin arcsin 4 0 1 π 6
kr H r Hi ki
y
Hale Waihona Puke Ht ktz
电磁场理论
第6章 均匀平面波的反射与透射
24
相位常数
故
3π 109 2 2 2 0 0 r 2 2 20π rad/m 8 3 10 E2 ex E2m cos(t 2 z ) ex Eim cos(t 2 z ) ex 0.667 10 cos(3π 109 t 20πz ) ex 6.67 cos(3π 109 t 20πz ) V/m
r2=10、
μr2 = 4、σ2= 0 。角频率ω＝5×108 rad /s 的均匀平面波
从媒质1垂直入射到分界面上，设入射波是沿 x 轴方向的线极化波， 在t＝0、z＝0 时，入射波电场的振幅为2.4 V/m 。求： (1) β1和β2 ； (2) 反射系数Г1 和Г2 ； (3) 1区的电场 E1 ( z, t ) ； (4) 2区的电场 E2 ( z, t ) 。 解:（1） 1 11 0 0
22
电磁能流密度 媒质1中沿 z 方向传播的平均功率密度 * 1 1 2 Siav Re Ei H i ez Eim 2 2
1
* 1 1 2 S rav Re Er H r ez 2 Eim 2 21 2 * 1 E im 2 S1av Re E H e (1 ) 1 1 z 2 2
2
2 4 0 r2 0 75.9π Ω 2 r2 10
2 1 75.9 60 0.117 2 1 60 75.9
（3） 1区的电场
E1 ( z ) Ei ( z ) Er ( z ) ex Eim (e j1z e j1z ) ex Eim [(1 )e j1z j2 sin( 1 z )] ex 2.4[1.117e j3.33 z j0.234sin(3.33 z )]
0
(3) 理想导体表面电流密度为
J S e z H1
z 0
200 jπ / 2 400 ex e ey ex j0.53 ey 1.06
0
0
电磁场理论
第6章 均匀平面波的反射与透射
21
例6.1.2
在自由空间，一均匀平面波垂直入射到半无限大的
电磁场理论
第6章 均匀平面波的反射与透射
65
例6.4.1 当垂直极化的平面波以角度i 由空气向无限大的理想 导电平面投射时，若入射波电场振幅为Eim ，试求理想导电平面 上的表面电流密度及空气中的能流密度的平均值。 解 令理想导电平面为 z = 0 平 面，如图所示。那么，表面电流 J S 为
Hi Ei Er
时的临界角θc ；（2）若入射角θi = θb ，则波全部透射
入空气。上述三种介质的θi =？ 解： 介质 水 玻璃 聚苯乙烯 临界角 c arcsin( 2 / 1 ) 布儒斯特角
b arc tan( 2 / 1 )
6.34 18.43
32
6.38 19.47 38.68
1
2 1
2 2
式中 1 0 , 2
又因为2区的波长 2
0 0 6 r r
r 0 r
1 2 0 3
r 1 r 9
r r 18
r r 36
2
电磁场理论
第6章 均匀平面波的反射与透射
故
imax arcsin( n n )
2 1 2 2
n2
i
t 1 1
n1
r1
电磁场理论
第6章 均匀平面波的反射与透射
61
例6.3.3 一平面波从介质1 斜入射到介质与空气的分界面，试 计算：（1）当介质1分别为水εr ＝81、玻璃εr ＝9 和聚苯乙烯ε
r ＝1.56
1 1 j z H r ( z ) (ez Er ) (ex 200e ey 100e j z e jπ / 2 )
0
0
电磁场理论
第6章 均匀平面波的反射与透射
14
在区域 z < 0 的合成波电场和磁场分别为
jπ / 2 E1 Ei Er ex j200e sin( z ) ey j400sin( z ) 1 H1 H i H r [ex 400 cos( z ) ey 200e jπ / 2 cos( z )]
电磁场理论
23 第6章 均匀平面波的反射与透射 例6.1.3 入射波电场 Ei ex 100 cos(3π109 t 10πz ) V/m ，从空
气（z < 0）中正入射到 z = 0 的平面边界面上。在z > 0区域中，
μr=1 、εr = 4 。求区域 z > 0的电场和磁场 。
电磁场理论
第6章 均匀平面波的反射与透射
27
或
j3.33 z E1 ( z ) Ei ( z ) Er ( z ) ex 2.4e ex 0.281e j3.33 z jt E1 ( z, t ) Re E ( z )e 1 8 ex 2.4 cos(5 10 t 3.33z ) ex 0.281cos(5 108 t 3.33z )
J S en H e z H
00
i r
0
Hr
x
z= 0
已知磁场的 x 分量为
z
Eim H x ex 2 cos i cos( k1 z cos i )e jk1 x sin i
求得
2 E im J S ey cos i e jk1 x sin i
1
0
电磁场理论
第6章 均匀平面波的反射与透射
66
能流密度的平均值 * * * 1 1 Sav Re( E H ) Re[ E y ( H x H z )] 2 2 已知垂直极化平面波的各分量分别为
E y e y j2 Eim sin( k1 z cos i )e jk1 x sin i Eim H x ex 2 cos i cos( k1 z cos i )e jk1 x sin i
1
入射波平均功率 密度减去反射波 平均功率密度
媒质2中的平均功率密度
2 * 1 Eim 2 S 2av Re E H e 2 z 2 2 2 2 1 2 2 1 (1 )(1 ) 由 2
S1av S 2av
可见入射角θi＝π/ 3大于临界角θc＝π/ 6 ，此时发生全反射。 入射的圆极化波可以分解成平行极化与垂直极化的两个线极 化波，虽然两个线极化波的反射系数的大小此时都为1，但它们的 相位差不等于±π/ 2，因此反射波是椭圆极化波。
电磁场理论
第6章 均匀平面波的反射与透射
58
例6.3.2 下图为光纤的剖面示意图，如果要求光波从空气进入 光纤芯线后，在芯线和包层的分界面上发生全反射，从一端传至 另一端，确定入射角的最大值。 解：在芯线和包层的分界面上发生全反射的条件为
无耗介质平面上，已知自由空间中，合成波的驻波比为3，介质内 传输波的波长是自由空间波长的1/6，且分界面上为驻波电场的最 小点。求介质的相对磁导率和相对介电常数。
1 解：因为驻波比 S 3 2 1 1 由于界面上是驻波电场的最小点，故 2 而反射系数 2 1
j z jπ/2 Ei ex 100e e ey 200e j z
则
1 1 j z H i ( z ) ez Ei (ex 200e e y 100e j z e jπ/2 )
0
0
电磁场理论
第6章 均匀平面波的反射与透射
1 c arcsin 2 / 1 arcsin(n2 / n1 )
由于 1
sin 1 sin c n2 / n1
n2 cos t sin c n1
r2
2
t
sin 1 sin( t ) cos t 2
2 2 2 2 sin n sin n 1 cos n 1 ( n / n ) n n 所以 i 1 t 1 t 1 2 1 1 2