任意方向传播的均匀平面波的极化方式识别
均匀平面波极化

y
y
E
Ey
O
Ex x
Ex x
O
Ey
E
(a) =0
(b) =
图6-6 线极化波电场的振动轨迹
众所周知,光波也是电磁波。但是光波不具有固 定的极化特性,或者说,其极化特性是随机的。光学 中将光波的极化称为偏振,因此,光波通常是无偏振 的。 为了获得偏振光必须采取特殊方法。
立体电影是利用两个相互垂直的偏振镜头从不同的 角度拍摄的。因此,观众必须佩带一副左右相互垂直 的偏振镜片,才能看到立体效果。
arc
tan
c
ost
c ost
kzx kzx
2
x
O
t kz x
图6-7 圆极化波电场的振动轨迹
这表明,对于给定z值的某点,随时间的增加,E ( z, t ) 的方向以角频率作等速旋转,其矢量端点轨迹为
圆,故称为圆极化(circular polarization)。当 时, / 2 ,t kz 的x 旋E向(z与,t)波的传播方向 成右手螺e旋z 关系,称为右旋圆极化波(righthanded circularly polarized wave);当
均匀平面波的极化
假设均匀平面波沿z方向传播,其电场矢量位于xy
平面,一般情况下,电场有沿x方向及沿y方向的两个
分量,可表示为
E Exme jx e jkzex Eyme jy e jkze y
(6-43)
其瞬时值为
Ex (z,t) Exm cost kz x (6-44a)
Ey (z,t) Eym cos t kz y (6-44b)
这两个分量叠加(矢量和)的结果随 x 、y 、Exm、Eym
的不同而不同。
第六章课件波的极化1

y
Ey
E
z
Ex x
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
设电场强度沿x、y方向分量的瞬时值分别为
E x E xm cos( t z) Ey Eym cos(t z )
在z=0的等相面上,有
Ex Exm cos t Ey Eym cos( t )
cost Ex
Exm
sin t
1 cos2 t
1
Ex Exm
2
E y cos(t ) cost cos sin t sin Ex cos
E ym
E xm
1
Ex E xm
2
sin
由此可得
Ex2 Ex2m
E
2 y
E
2 ym
2Ex Ey Exm Eym
cos
sin 2
这是一个椭圆方程。合成场强矢量E的末端在 一个椭圆上旋转。
根据Ψ取值的不同,可得所谓的线性极化波、 圆极化波和椭圆极化波。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店 铺)
(1)线性极化波
0或 ,在z=0的等相面上,则有
E y E ym cos t Ex Exm cos t
它们的合成电场强度的幅值为
Eቤተ መጻሕፍቲ ባይዱ
E
2 x
E
2 y
E
2 xm
E
2 ym
cos
t
合成场强与x轴的夹角则为
tg 1 E y tg 1 E ym
Ex
E xm
(2). 圆极化波
若 ,且
tg 2
2E xm E ym
均匀平面波的极化特性

6.6 均匀平面波的极化特性1.电磁波的极化定义2.电磁波的极化形式1.电磁波的极化定义电磁波的极化是指空间某点的电场强度矢量方向随时间的变化规律。
用空间某点电场强度矢量的端点随时间变化所描画出的轨迹来表示。
电磁波的极化特性在日常生活中也经常使用例如:超短波收音机U E l =⋅θElcos E l =⋅θ均匀平面波的极化特性平面波的表达式:mˆcos()xE E t kz a =-+ωϕmˆcos()yH H t kz a=-+ωϕxyz2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
yx2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
(2)圆极化:电场强度矢量端点随时间变化的轨迹是圆。
yEx2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
(2)圆极化:电场强度矢量端点随时间变化的轨迹是圆。
(3)椭圆极化:电场强度矢量端点随时间变化的轨迹是椭圆。
yx(1)线极化假设空间任意一个平面波:x yE E E =+若电场表示为:m ˆcos()x x x x E E t kz a ϕ=ω-+演示1——x 方向的线极化波m ˆcos()y y y y E E t kz aϕ=ω-+演示2——y 方向的线极化波线极化条件:ϕϕϕ==y x 或x y ϕϕπ-=±两个相互垂直线极化波叠加:条件:ϕϕϕ==y x 22mmcos()x y E EEt kz ωϕ=+-+与x 轴的夹角为:E θarctan()ymxmE E θ=x yE E E =+m ˆcos()x x x x E E t kz aϕ=ω-+m ˆcos()y y y y E E t kz aϕ=ω-+其中:结论:两个相互垂直线极化波叠加,其初始相位相同时,形成新的线极化波。
两个相互垂直线极化波叠加:条件:22mmcos()x y E EEt kz ωϕ=+-+与x 轴的夹角为:E θarctan()ymxmE E θ=-x yE E E =+m ˆcos()x x x x E E t kz aϕ=ω-+m ˆcos()y y y y E E t kz aϕ=ω-+x y ϕϕπ-=±其中:结论:两个相互垂直线极化波叠加,其初始相位相同时,形成新的线极化波。
3.2波的极化

E x = E m cos(ω t + ψ x )
r sin(ω t + ψ x )
的幅度为: E = E + Ey = Em 幅度为
2 x 2
不变
4
∴ Ex + Ey = Em
2 2
2
圆方程
α = arctan
Ey Ex = ± (ω t + ψ x )
E x m E y m ω s in ψ dα = dt E x m 2 c o s 2 (ω t + ψ ) + E y m 2 c o s 2 (ω t )
3、左旋、右旋椭圆极化波: 、左旋、右旋椭圆极化波:
z 固定, (z =0), t 变化: 固定, 变化:
2012-3-19
见书85面 dα 右旋。 0 < ψ < π , > 0, 右旋。 dt dα 8 左旋。 −π < ψ < 0 , < 0, 左旋。 dt
7
ψ
任意, 任意, E
xm
≠ Eym
X 2 2XY Y 2 ( ) − cosψ + ( ) = sin2ψ Exm ExmEym Eym
合成电场与x轴夹角: 合成电场与 轴夹角:ta n α = 轴夹角
最普通的 椭圆方程: 椭圆方程
E y m c o s (ω t ) E x m c o s (ω t + ψ )
r E与
x 轴的夹角
y
3、右旋、左旋圆极化波: 、右旋、左旋圆极化波: 当 ψ x −ψ
=
π
2
时 , α = ω t + ψ x 右旋圆极化波
(电场矢端旋转方向与电波传播方向成 右手螺旋关系) 当 ψ x −ψ
任意方向波的极化识别

任意方向波的极化识别姓名唐浩月学号 **********日期 2011/6/17【摘要】在教材中,我们已经学习掌握了沿坐标轴方向传遍的电磁波的极化识别,本文主要对此作一定的延伸拓展,在复述域上进行针对沿任意方向传播的电磁波进行极化识别。
【关键词】电磁波 任意方向 直线极化 圆极化 椭圆极化 左旋 右旋 【引言】由于教材中已经详细解释推导了沿 z 方向传播的电磁波的各种极化情况及识别,针对更一般的情况,本文将着重讨论任意方向平面波的极化识别问题,达到将电磁波的极化概念进行推广的目的。
【正文】一:任意方向传播电磁波表达式针对沿任意方向传播的电磁波,其传播方向依然与等位面垂直,在等相位面内的任意一点电磁场的大小和方向均相等,这些都是和传播方向的坐标系选取无关的。
故,不妨令传播方向的单位矢量为e n →,定义一个波矢量k →,其大小为相位常数k ,方向为e n →,即:e e e e n x x y y z z k k k k k →→→→→=⋅=⋅+⋅+此时,沿着z 方向传播也包含在内,为此方程的一个特殊情况。
如此一来,可以将沿着任意方向-传播的均匀平面波的电场矢量写成以下形式:e ()n jk rj k rm m E r E eE e→→→→→→→-⋅-⋅=⋅=⋅对应的磁场矢量为:11()e ()e j k rn n m H r E r E eηη→→→→→→→→-⋅=⨯=⨯⋅由于传播方向任意,故在波的分解时需要引入复数知识,不妨令m mr ml E E j E →→→=+,即将电厂矢量分解为实部和虚部以方便后文中的讲解。
其中j k re→→-⋅为传播因子。
二:极化识别 1 直线极化波由直线极化的概念可知,直线极化波的合成波()E r →的强度可以不断变化,但是其合成方向角是恒定不变的。
对于合成波()E r →来说,只有当mr ml E C E →→=(C 为常数),即()0mr ml k E E →→→⋅⨯=时,其幅角主值不变,为直线极化波。
讲16均匀平面波极化

0 < ϕ x − ϕ y < π 右旋椭圆极化
− π < ϕx −ϕ y < 0
左旋椭圆极化
两个空间上正交的线极化波可合成一个椭圆极化波;反之亦然。 两个空间上正交的线极化波可合成一个椭圆极化波;反之亦然。 两个旋向相反的圆极化波可合成一个椭圆极化波; 两个旋向相反的圆极化波可合成一个椭圆极化波;反之一个椭圆 那极化波可分解为两个旋向相反的圆极化波。 那极化波可分解为两个旋向相反的圆极化波。
一个圆极化波可以分解为两个相位相差90度 振幅相等、 一个圆极化波可以分解为两个相位相差90度、振幅相等、空间 90 上正交的线极化波。两个相位相差90度 振幅相等、 上正交的线极化波。两个相位相差 度、振幅相等、空间上正交的 线极化波。可以合成为一个圆极化波。 线极化波。可以合成为一个圆极化波。
r π r r E (t ) = ex E0 cos(ωt + ϕ x ) + e y E0 cos(ωt + ϕ x + ) 2
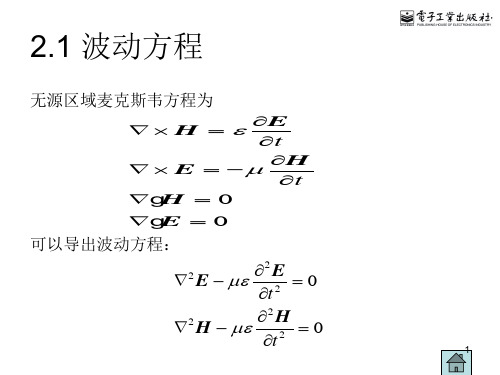
5.2 电磁波的极化
电场强度矢量随时间变化的特性称为电磁波的极化。 电场强度矢量随时间变化的特性称为电磁波的极化。 极化 根据电场强度的矢端曲线的形状,线极化、圆极化、椭圆极化。 根据电场强度的矢端曲线的形状,线极化、圆极化、椭圆极化。 均匀平面波
r r r r r E = ex E x + e y E y = (ex E x 0 + e y E y 0 )e − jkz
圆极化波,电场的旋向与波的传播方向 成右手螺旋 圆极化波,电场的旋向与波的传播方向-z成右手螺旋
r r r π (3) E ( z , t ) = e x E m cos(ωt − kz ) + e y E m sin(ωt − kz + ) 4
平面波的极化形式
故平均功率流密度可表示为
Sav
1 2
E
2ez
1
1 2
E
2v
p
在无界的理想介质中,式中的
1 2
E
2(或
1 2
H 2
)
表示理想介质中的总的平均能量密度。平
均电能密度为 1 E2 ,平均磁能密度为 二者各占一半。4
1 H2
4
13
2、沿任意方向传播 应该指出,并不是在任何情况下设
定波的传播方向为直角坐标系的某 个坐标轴方向都是方便的。譬如将 要讨论的波对分界面斜入射问题, 在设定分界面与某个坐标面平行后, 波的传播方向就只能是任意方向。
1
2
1
2
1
可见相速度不仅与媒质参数有关,还与频率有关。导电 介质是色散媒质。
导电介质中的平均功率流密度矢量为
Sav
1 2
Re E
z
H
z
1 2
Re
ex
Exme
k
''
ze
jk ' z
ey
Exm
c
ek ''ze
可看H出 z和,t 存 R在e 一H 个z相e jt位 差ey。Excm下e图k''z 绘cos出t某 k时' z刻的 图
形,可以看出它们的振幅随传播距离z的增大而 按指数规律衰减。
图2.2.7 导电介质中波的传播
22
导电介质中,波的相速度为
vp k '
均匀平面波沿空间各点的极化方向

任意传播方向的均匀平面波极化方向的识别【摘要】:本文讨论了均匀平面波在空间的极化方向。
从电场分量的相位和振幅的情况对电磁波的极化形式进行了分类。
对所学知识进行了小结【关键词】:电磁波的极化 线极化 圆极化 椭圆极化【正文】电磁波的极化:电磁波在传播的过程中,在垂直于传播方向上电场可能会有两个或以上的分量。
由于每个分量的振幅和相位不一定相同。
因此,在空间任意给定点上,合成波电场矢量E 的大小和方向都可能随时间变化,这种现象成为电磁波的极化。
电磁波的极化是电磁理论中的一个重要概念,它表征在空间给定点上电场强度矢量的取向随时间变化的特性,并用电场强度矢量的端点随时间变化的轨迹来描述。
电磁波的极化形式取决于y E 和x E 分量的振幅之间和相位之间的关系。
下面分别从相位和振幅来讨论电磁波的极化形式。
(为了简化问题以下取z=0点来讨论)1πφφ±=-或0x y则矢端参数方程转化为合成波电场与x 轴的夹角为为常数 当时取负号时取正号,πφφφφ±=-=-x x y y 0合成电场的端点在一条直线上运动,如图所示m m arctan()y x E E α=±2222m m (0,)(0,)cos()x y x y y E E t E t E E t ωφ=+=++结论:任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相位相同或相差为±π时,其合成波为线极化波。
2x 和y 分量的振幅相等且2πφφ±=-x y )()E E (arctan x E E )sin()2cos(E )cos(E 2222y y x x y m y x x m x m y x m x x x t constE E t E t E t E φωαφωπφωφωπφφπφφ+-====+=+-=++=+=+==-轴的夹角为合成波电场与大小为故合成波的电场强度的时,即当由此可见,合成波电场的大小不随时间变化,但方向却随时变化,其端点轨迹在一个圆上并以角速度ω旋转,故为圆极化波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
均匀平面波 极化 矢量分析
������ ∙ ������������������ × ������������������ > 0,合成波为右旋极化; ������ ∙ ������������������ × ������������������ = 0,合成波不旋转,为线极化; ������ ∙ ������������������ × ������������������ < 0,则为左旋极化。 对于非线极化情况,需要进一步确定极化波是否为圆极化。如果下列两式满 足,则为圆极化,否则为椭圆极化: ������������������ = ������������������ ������������������ ∙ ������������������ = 0 这种判断方法,不需画图;不需关心分量及初相位;适合任何情况,求计算 简单。
即在 x,y 方向上,电场振幅和相位都不等的情况。 6. 推广到任意方向。 任意方向传播的均匀平面波,可表示为:
-jk r j t E (r , t ) Re[ Eme e ] e x Exm cos(t k r ex ) e y E ym cos(t k r ey ) ez Ezm cos(t k r ez )
【结束语】
电磁场的极化有广泛地应用。能够快速准确地判断任意方向传播的均匀平面 波的极化方式,可以简化计算和抽象思维难度,方便解决问题。本文讨论的方法 应用范围极广,且计算量小,不需画图,可以用作解决均匀平面波极化方式的问 题。但是本文用到复矢量分析的方法,对思维和基础知识要求较高,完成过程中 遇到很多困难,许多地方似懂非懂,解决得不够彻底,今后还将完善。
合成波电场������ = ������������ Ex + ������������ Ey 。 由于Ex 和 Ey 分量的振幅和相位不一定相同, 因此,在空间任意给定点上,合成波电场强度矢量������的大小和方向都可能会 随时间变化,这种现象称为电磁波的极化。 它表征,空间固定点处,电场强度的矢端随时间变化的轨迹。矢端的时 间变化规律,决定于各分量幅度和初相的大小。
【正文】
1. 极化的概念。 以沿 Z 方向传播的均匀平面波为例,假设������ = ������������ Em cos (ωt − kz + φ)。 在任何时刻, 此波的电池强度矢量������的方向始终保持在 x 方向。 一般情况下, 沿 z 方向传播的均匀平面波的Ex 和 Ey 分量都存在,可表示为: Ex = Exm cos ωt − kz + φx Ey = Eym cos (ωt − kz + φy ) (1) (2)
极化的状态:
E ym d ( sin ) 2 dt Exm cos (t kz x ) sin , y x
波都沿 z 方向传播,则有: ∆φ = 0 or ± π:线极化 0 < ∆������ < ������:左旋极化 −π < ∆������ < 0:右旋极化 3. 线极化波。 条件:∆φ = 0 or ± π 则矢端参数方程简化为: 2 2 2 2 E Ex (0, t ) E y (0, t ) Ex m E ym cos( t y ) 合成波电场与 x 轴的夹角为: E arctan( ym ) Exm 任何两个同频率、同传播方向且极化方向互相垂直的线极化波,当它们的相 位相同或相差为±π 时,其合成波为线极化波。 4. 圆极化波。 条件:Exm = Eym = Em 、∆φ = ± 2 矢端方程:
2. 关于 Z 轴方向传播的均匀平面波的极化方式。 首先我们引入矢端参数方程。在直角坐标系下,矢端参数方程为:
Ex (t ) Exm cos( t kz x ) E y (t ) E ym cos( t kz y ) 在极坐标系下: E (0, t ) E 2 cos 2 ( t ) E 2 cos 2 ( t ) xm x ym y E ym cos(t kz y ) ] (t ) arctan[ Exm cos(t kz x )
2 2 2 Ex Ey Em
π
φy − φx = ∆φ =
π 2 π
为左旋极化波 为右旋极化波
φy 同频率、同传播方向且极化方向互相垂直的线极化波,当它们 的振幅相同、相位差为±π / 2 时,其合成波为圆极化波。 5. 椭圆极化波。
2 Ey 2 Ex E y Ex2 2 cos sin 2 2 Exm E ym Exm E ym
【参考文献】 《电磁场与电磁波》
《复变函数论》
谢处方,饶克谨
钟玉泉
设其中
������������ = ������������������ + j ������������������ 为复振幅矢量,������������������ 和������������������ 分别为其实部和虚部,且均
为实矢量;e−j ������∙������ 为传播因子。 根据电场的表达式,首先求出 k, ������������������ 和������������������ .然后就可以根据������ ∙ (������������������ × ������������������ ) 的符号来判断旋向。
【引言】
《电磁场与电磁波》 (谢处方,饶克谨)教材中,关于均匀平面波的极化的 讨论,仅限于沿 Z 轴方向传播,有很大的局限性——实际生活中,电磁波是可以 沿任意方向传播的。 但是书中关于 Z 轴方向传播的均匀平面波讨论很详细,值得 借鉴。因为,任意方向传播的均匀平面波可以抽象为重新建立坐标系,将传播方 向固定为 Z 轴,则可以用相同的讨论方法确定波的极化方式。
