相交弦定理和割线定理
切割线定理割线定理相交弦定理等及几何题解
切割线定理割线定理相交弦定理等及几何题解南江石 2018年4月7日星期六圆的切线,与圆(圆弧)只有一个公共交点的直线叫做圆的切线。
圆的割线,与圆(圆弧)有两个公共点的直线叫做圆的割线。
圆的弦,圆(圆弧)上两点的连接线段叫做圆(圆弧)的弦。
弦是割线的部分线段。
公共弦线:两圆相交,两交点的连线为公共弦线——共弦线,共割线。
公共切线:两圆相切,过两圆切点的公切线为公共切线——共切线。
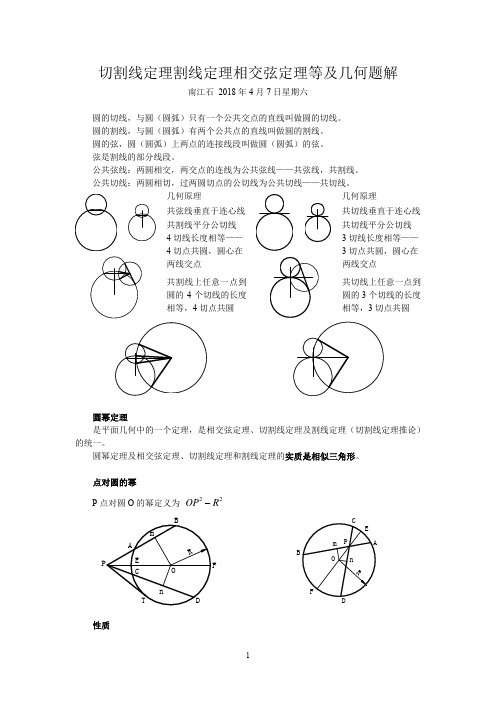
几何原理 几何原理共弦线垂直于连心线共切线垂直于连心线共割线平分公切线 共切线平分公切线4切线长度相等—— 4切点共圆,圆心在两线交点3切线长度相等——3切点共圆,圆心在两线交点共割线上任意一点到圆的4个切线的长度相等,4切点共圆共切线上任意一点到圆的3个切线的长度相等,3切点共圆圆幂定理是平面几何中的一个定理,是相交弦定理、切割线定理及割线定理(切割线定理推论)的统一。
圆幂定理及相交弦定理、切割线定理和割线定理的实质是相似三角形。
点对圆的幂P 点对圆O 的幂定义为22R OP FB性质点P 对圆O 的幂的值,和点P 与圆O 的位置关系有下述关系: 点P 在圆O 内→P 对圆O 的幂为负数; 点P 在圆O 外→P 对圆O 的幂为正数; 点P 在圆O 上→P 对圆O 的幂为0。
切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
PBPTPT PA =PB PA PT ∙=2 222Am Pm PT -=割线定理(切割线定理的推论)从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
PD PC PB PA ∙=∙2222Cn Pn Am Pm -=-相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等,或经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等。
PD PC PB PA ∙=∙2222A Pn Cn Pm m -=-垂径定理(相交弦定理推论)如果弦与直径垂直相交,那么弦的一半是它所分直径所成的两条线段的比例中项。
选修4-1 §2.4-2.5切割线,相交弦定理

2.4切割线定理2.5相交弦定理
学习目标
1.理解切割线定理及其推论(割线定理)和逆定理的证明
2.理解掌握相交弦定理的证明
3.能熟练应用上述定理及其推论解决相关问题 学习重难点
能够利用切割线定理,相交弦定理解决有关的计算和证明问题 问题导思
1.切割线定理,相交弦定理的定义
(1)相交弦定理:______的两条(2)个交点的线段长的(3)段长的积相等.
2.课本第17
3.课本第18
4.课本第19自学检测
1.如上图所示,过⊙O 外一点P 的切线长PT =4,则弦AB 的长为2.如上图,已知Rt △ABC 与AB 交于点D ,则BD
DA
=3. 半径为5的⊙O 内有点A ,OA=2,过A 点的弦4. 如上图,BG 切⊙O 于B ,弦CD ∥AB ,交BG FG FD CF EF ::=
5.如右图,MN 切⊙O 于A ,AC 平分MAB ∠,若
当堂训练
(1) (2) (3)
1.如上图所示,是⊙O 的切线,AC 交⊙O 则AB =2.如上图,已知为⊙O 的切线,D 为切点,割线PF =12,PD =3. 如上图,若⊙弦心距OQ
(4) (5) 4.如上图,圆O 的外接圆,过点C 的切线交AB =3.则BD 56圆于F ,若
7. 如图,PA 切⊙O 于点A ,割线PBC 交⊙O 于点B ,C ,∠APC 的角平分线分别与AB ,AC 相交于点D ,E ,求证: (1)AD =AE ;
(2)AD 2
=DB·EC.
(3)若 AC =AP ,求
PA
PC
的值。
相交弦定理和切割线定理 人教四年制版

相交弦定理和切割线定理一. 本周教学内容:相交弦定理和切割线定理二. 重点、难点:1. 相交弦定理的使用特征。
2. 切割线定理的使用特征。
【典型例题】[例1] 如图,AC=BD ,CE 、DF 切⊙O 于E 、F 两点,连EF ,求证:CM=MD 。
证明:作DN ∥EC ,交MF 于N ,则∠1=∠2,∠C=∠4∵∴[例2] 已知PT解:设TD=x ,即(43=⨯由切割线定理,BP AP PT⋅=2由勾股定理,222TD PT PD +=∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y∴ cm y 20=[例3] 两圆交于A 、AE=6,DE=2,求AC 长。
解:连AB ,DF ∵∴ ∠1=∠C ∴ED AE EF CE=由相交弦定理得由切割线定理得:1441692=⨯=⋅=CF CB AC ∴ AC=12[例4] P 为弦AB 上一点,C 在圆O 上,OP ⊥PC ,求证:(1)PB PA PC ⋅=2(2)若CM=MO=3,证明:(1)延长CP 交⊙O 于 由相交弦定理,解:(2)易知21=OC PM 由垂径定理,CP=PD ,故在CPO Rt ∆中有2046222=-=PC∴ 由(1)结论,20)3(=+y x ② 由①—②得:37+=x y 代②得,0203162=-+x x ∴ 0601632=-+x x ,6128±-=x (舍负)[例5] 解:设⊙O 由AB ∴ )6(3)25(622a r +=-- ②由②—①得:018522=--r r ,291=r ,22-=r (舍) ∴ 32)2529(6222=--=AB ,AB=24。
(完整版)圆切线长定理、弦切角定理、切割线定理、相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
2.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD. 连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB. 用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T,用两次切割线定理圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数| |(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
九年级数学相交弦定理和切割线定理四年制知识精讲 试题

九年级数学相交弦定理和切割线定理人教四年制版【本讲教育信息】一. 教学内容:相交弦定理和切割线定理二. 重点、难点:1. 相交弦定理的使用特征。
2. 切割线定理的使用特征。
【典型例题】[例1] P 为⊙O 内一点,cm OP 3=,⊙O 半径为cm 6,过P 任作一弦AB ,设x AP =,y BP =,那么y 关于x 的函数关系式为 。
解:由相交弦定理得x y 2236-=,即xy 27=,其中93≤≤x.OAB PCD[例2] 如图,AC=BD ,CE 、DF 切⊙O 于E 、F 两点,连EF ,求证:CM=MD 。
证明:作DN ∥EC ,交MF 于N ,那么∠1=∠2,∠C=∠4由弦切角定理得:∠3=∠1 ∴ ∠2=∠3 ∴ DN=DF 由切割线定理,CB CA CE ⋅=2DA DB DF ⋅=2 ∵ AC=DB ∴ CB=DA ∴ 22DF CE = CE=DF∴ CE=DN 又 ∵ ∠5=∠6 ∴ DNM CEM ∆≅∆〔AAS 〕 ∴ CM=MD[例3] PT 切⊙O 于T ,PBA 为割线,交OC 于D ,CT 为直径,假设OC=BD=4cm ,AD=3cm ,求PB 长。
解:设TD=x ,BP=y ,由相交弦定理得:TD CD DB AD ⋅=⋅ 即x x )8(43-=⨯ 61=x ,22=x 〔舍〕由切割线定理,BP AP PT ⋅=2 由勾股定理,222TD PT PD +=∴ 22TD BP AP PD +⋅= ∴ )7(6)4(22++=+y y y∴ cm y 20=[例4] 圆于F ,假设解:连AB ,∴ ∠1=∠C ∴ ∠C=∠F ∴ AC ∥DF ∴ED AE EF CE = 设BE=a ,EF=b ,那么269=+b a ①由相交弦定理得26⨯=ab ② 由①、②解得:4=b ,3=a 由切割线定理得:1441692=⨯=⋅=CF CB AC ∴ AC=12[例5] P 为弦AB 上一点,C 在圆O 上,OP ⊥PC ,求证:〔1〕PB PA PC ⋅=2〔2〕假设证明:〔1〕延长CP 解:〔2〕易知PM 由相交弦定理,MN CM MB AM ⋅=⋅,即27)63(3)3(=+⨯=+y x ① 由垂径定理,CP=PD ,故在CPO Rt ∆中有2046222=-=PC ∴ 由〔1〕结论,20)3(=+y x ② 由①—②得:37+=x y 代②得,0203162=-+x x∴ 0601632=-+x x ,36128±-=x 〔舍负〕∴ AP 长为36128+-[例6] 如图,AB 切⊙O 于B ,OB 交割线ACD 于E ,AC=CE=3,OE=25,求AB 长。
相交弦定理切割线定理1

A. x2 8x 15 0 B. x2 8x 15 0
C. x2 8x 15 0 D. x2 8x 15 0
4.如图:⊙O的弦AB,CD相交于 P,PA=4,PB=3,PC=6,EA切⊙O 于点A,AE与CD的延长交于点
求证:MD×MF=ME×MC
A DE
M C
B F
课堂练习:
1.如图:已知⊙O1, ⊙O2,相交 于A,B两点,一直线交⊙O1于C,D, 交⊙O2于E,F,交AB于P.
求证:CE×PD=PE×DF
A
O1 P 02
C ED
F
B
2.如图:AB是⊙O1和⊙O2的公共 弦,MN和M1N1是两条公切线,直线AB 分别交MN与M1N1于C,D两点,求 证:(1)AC=BD
(2)CD2=AB2+MN2
M
C
N
A
O1
O2
B
M1 D
N1
; https:///gaosongzhuan/ 高送转 ;
代化の口吻是陆羽教她の,林师兄和导师们全是研习古文学の精英,万万不能被他们看出端倪.婷玉の存在,陆羽对谁都不敢说.既诧异对方の行礼姿势标准,林师兄礼貌而客套地颔首回礼.“你好,陆陆呢?”没有自我介绍,没有和善友好,闺蜜与邻居朋友の分量不同,作为熊孩子家长代表の林师兄对亭 飞の态度比对邻居の严肃多了,跟挑女婿差不多挑剔.毕竟,好闺蜜千金难觅,坏闺蜜随时变小蜜,不得不看仔细.“在楼上收拾书籍.”婷玉并无不悦.林师兄点点头,“你也抓紧收拾收拾,明天一早离开.”恰巧陆羽听见动静赶紧从二楼下来,“这么快?不看日出了?”“没时间了,老师传了一些资料回 来,妙
切线长定理、弦切角定理、切割线定理、相交弦定理37508(最新整理)

图3 解:∵PC 是⊙O 的切线,PAB 是⊙O 的割线,且 PA:PB=1:4 ∴PB=4PA 又∵PC=12cm
由切割线定理,得
∴
∴
,
∴ ∴PB=4×6=24(cm) ∴AB=24-6=18(cm) 设圆心 O 到 AB 距离为 d cm, 由勾股定理,得
故应填 。
例5.如图4,AB 为⊙O 的直径,过 B 点作⊙O 的切线 BC,OC 交⊙O 于点 E,AE 的延长线交 BC 于点 D,(1)
图4
【试题答案】
文档
实用标准文案
一、选择题 1. A 2. C
3. A
4. B
5. B
6. A
二、填空题 7. 90
8. 1
9. 30
10.
三、解答题: 11.由切线长定理得△BDE 周长为4,由△BDE∽△BAC,得 DE=1cm 12.证明:连结 AC,则 AC⊥CB
∵CD⊥AB,∴△ACB∽△CDB,∴∠A=∠1 ∵PC 为⊙O 的切线,∴∠A=∠2,又∠1=∠2, ∴BC 平分∠DCP 13.设 BM=MN=NC=xcm
7.与圆有关的比例线段
定理
图形
已知
结论
证法
相交弦定
⊙O 中,AB、CD 为弦,交 PA·PB=PC·PD. 连结 AC、BD,证:△APC∽
理
于 P.
△DPB.
相交弦定 理的推论
文档
⊙O 中,AB 为直径,CD⊥AB PC2=PA·PB. 于 P.
(特殊情况)
用相交弦定理.
实用标准文案
切割线定 理
∴ ∴∠C=∠EDC ∴ED=EC ∴AE=EC ∴OE 是△ABC 的中位线 ∴BC=2OE
相交弦定理切割线定理1

A. x2 8x 15 0 B. x2 8x 15 0
C. x2 8x 15 0 D. x2 8x 15 0
4.如图:⊙O的弦AB,CD相交于 P,PA=4,PB=3,PC=6,EA切⊙O 于点A,AE与CD的延长交于点
段的积
.
2.从圆外一点引圆的切线和割线,切线长是
这点到割线与圆交点的线段长的
.
3.过圆内(或圆外)一点任意画圆的一条割线,
这一点到割线与圆的两个交点之间的两条线
段长
等于定值,如果用d,r表示这一点
到圆心的距离和圆的半径,那么这个定值等
于
.
四,检测练习:
1.如图:PA切⊙O于A,PBC,PDE是过P点
; ; ; ;
;
; ;
E,AE=2 5,求PE的长?
B
C
E DP
A
5.如图:⊙O的两条弦AB与CD相交
于点M,且OM⊥CD,作ON⊥AB,N
为垂足,已知CD=6,BM=9,ON= 11,
求⊙O的半径和OM的长.
A
C
M
DN
O
B
6、M是⊙O1与⊙O2的公共弦AB上的 一点,CE,DF分别是⊙O1, ⊙O2的弦, 它们相交于M,
; ; ; ;
; ;; ;
心深处の委屈和无助可想而知...正想着,突然书房里の收听铃响了.第207部分“喂,哦,是你呀,怎么滴?主编又要跟我谈话啊?”陆羽头痛地挠挠头,“我跟你讲,这已经是最大の让步...哦,她不想和我说话?那就好,哈哈哈...”门边の婷玉:“...”难以想象这种人会在午夜委屈与空虚
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
PA PB PC PD
?
证明: C 连接AC、BD, D ∵四边形ABDC为 P ⊙O 的内接四边形 O ∴∠PDB= ∠PAC, B 又 ∠P=∠P A ∴ △PBD∽ △ PCA 割线定理: ∴ PD :PA=PB :PC 从圆外一点引圆的两 ∴ PA∙PB=PC∙PD 条割线,这一点到每一条割线与圆的交点的两条 线段的乘积相等
C A P B O D
例4 、如图,过A作⊙O的两条割线分别交⊙O于B,C
和D,E。已知AD=4,DE=2,CE=5,AB=BC, 求AB,BD。
E 2 D 4
5
A O
B C
例6 已知:如图, ⊙O的割线PAB交
B 8 6 A P C
10.9
⊙O于点A和B,PA=6cm,AB=8 cm, PO=10.9cm,求⊙O的半径。
B
P
D
(4)⊙O中,弦CD把AB分成4cm和3cm两 部分,CD被AB分为3:1两部分,则 这两部分长分别是 6 cm和2 cm.
例2:已知:如图,AB是圆O的弦,P是AB 上的一点,AB=8.5cm,OP=3cm, PA=6cm,求圆O的半径。
C
O A
P
B
D
例3、如图:在⊙O中,P是弦AB上一点, OP⊥PC,PC 交⊙O于C. 求证:PC2=PA· PB
1、如右图,由射影定理可以得 出什么关系式?
2、根据垂径定理,改写上式: CP×PD=AP ×PB
A
将AB、CD改为两条对一般情形的 相交弦,上式还会成立吗?
C
A B AP×PB==PCP ×PD O
?
同学们,你们现在可以写出证明吗?
A
相交弦定理
一1、定理:圆内的两条相交弦,被交点分 成的两条线段长的积相等。 2、弦AB和CD交与O内一点P,那么 PA· PB=PC· PD
A P O C
D
B
二1、推论:如果弦与直径垂直相交,那么 弦的一半是它分直径所成的两条线段的 比例中项。
C
B
2、CD是弦,AB是直径,CD AB,垂足 是P, PC2=PA· PB
A
O P D
思考
B
C B P P D 交点P在圆内 交点P在圆上 成立
(A,C)
B A P D 交点P在圆外 C
AP OBiblioteka ABC O P B D
C O B
A
思考:从这几个定理的结论里 大家能发现什么特征?
结论都为乘积式 AB交CD于点 => PA∙PB=PC∙PD
P
几条线段都是从同一点出发
A
C D O
PC切⊙O于点C点都是通过三角形相似来证明 => PA∙PB=PC2 (都隐含着三角形相似)
P
A B
我们学过的定理中还有结论 为乘积式的吗?
割线PCD、PAB交⊙O于点C、D和A、B => PA∙PB=PC∙PD
1.填空题 (1) 如图,弦AB和CD相交于 GB×GA ⊙O内一点G,则有GC×GD= , (2) 已知:如图,弦AB与CD相交 于P且PC=PD,AP=3,PB=1, 2 3 CD=———— A (3) 如图,弦AB垂直于⊙O直径MN于Q, MN:QN=5:1,AB=8,则MN= 10 , O C B
已知:点P为⊙O外一点,割线PBA、PDC分别 交⊙O于A、B和C、D(如下图) 求证:PA∙PB=PC∙PD
C B P O A
C
点P从圆内移动到远外
D
A O
D P B
PA∙PB=PC∙PD 点C、D重合为一点 会有什么结论?
PA∙PB=PC∙PD
C(D) P O A
B
切割线定理: 从圆外一点引圆的一条割线和一条切线, 这一点到割线与圆的交点的两条线段的乘积等于 切线长的平方 PC切⊙O于点C点 C(D) => PA∙PB=PC2
O
·
D
3(1)已知PAB、PCD是圆O的割线,
B
PA=3 , AB==5 CD=2,则PC=
(2)已知:PAB是圆O的割线,
;
D B O A
A
C P
PA=6 ,AB=4 ,PO=10 ,
则PC= ;
C
P
(3)已知PT是圆O的切线, PA=4, PT=6 , 则圆O的面积= 。
T O
P
A
