第3章- 第2讲地图投影基本理论汇总
(地图学课件)第2讲(第三章常用的地图投影)

§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影(墨卡托投影) 3、等角航线
在该投影图上,不仅保持了方向和相对位置的正确,而且能使等角航线表 示为直线,因此对航海、航空具有重要的实际应用价值。只要在图上将航 行的两点间连一直线,并量好该直线与经线的夹角,一直保持这个角度即 可到达终点。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.1 等差分纬线多圆锥投影
2、变形特点
• 该投影是属于面积变形不大的任意投影,从 整体构图上有较好的球形感; • 陆地部分变形分布比较均匀,其轮廓形状比 较接近真实,并配置在较为适中的位置,完整 地表现了太平洋及沿岸国家,突出了我国与太 平洋各国之间的联系; • 中央经线和±44纬线的交点处没有角度变形 ,我国境内绝大部分地区的角度变形在10以 内,只有少数地区可达13左右 ; • 面积比等于1的等变形线自西向东贯穿我国中 部,我国境内绝大部分地区的面积变形在10% 以内 。
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
3. 地图的内容 主题和内容不同,对投影的要求也不同。
• 要求方向正确,应选择等角投影 • 要求面积对比正确,应选择等积投影 • 教学或一般参考图,要求各方面变形都不大,则 应选择任意投影
现代地图学教程 第3章 地图投影及其判别与变换
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
2.制图比例尺 不同比例尺地图对精度要求不同,投影亦不同。 大比例尺地形图,对精度要求高,宜采用变形小的投影
地图投影基本知识

由以下两个式子计算α:
sin cos0 cos sin 0 cos( 0 )
sin Z cos cos(90 ) sin(90 0 ) sin(90 ) cos(90 0 ) cos( 0 )
正弦定理:
sin Z sin(90 ) sin( 0 ) sin sin Z sin cos sin( 0 )
(3)地图投影的变形 我国1984年编制的世界地图
(3)地图投影的变形:微分圆到变形椭圆
微分圆
形状不变: 等角投影
某个方向 长度不变
面积不变
都改变
地球表面经投影以后在长度、角度和面积要发生一定程度的变形。
长度变形
角度变形
面积变形和长度变形
投影变形示意图
① 长度比和长度变形
② 面积比和面积变形
(3)球面坐标系的常用公式
P Q(φ ,λ )
0 0
α Z A(φ,λ)
W
E
Q’ P’
球面上任意点,既可用 大地坐标(,)表示, 也可以用球面极坐标( ,Z)来表示。
(3)地图投影分类 ① 按投影面划分
方位投影:投影面为平面 圆锥投影:投影面为圆锥面 圆柱投影:投影面为圆柱面 伪方位投影
OA方向的长度比:
OA方向的角度变形:
x r cos y r sin
x ax y by
OA方向的角度变形: x r cos y r sin
x ax y by
y by b tan tan x ax a
OA方向的角度变形:
sin( ) b tan tan cos cos tan (1 a ) sin( ) b tan tan tan (1 ) cos cos a
02第03章 地图投影的基本原理

第三章地图投影的基本原理§1 1 地图投影基本概念地图投影基本概念地图投影基本概念§2 2 地图投影基本理论地图投影基本理论地图投影基本理论§1 地图投影基本概念一、地图投影的概念和实质二、地图投影的研究对象及任务地图投影——在球面与平面之间建立点与点之间对应函数关系的数学方法。
研究地图投影的理论、方法、应用和变换等学问的科学,称地图投影学或数学制图学。
{),(),(21λϕλϕf y f x ==一、地图投影基本方法1.几何透视法——利用透视线的关系,将地球体面上的点投影到投影面上的一种投影方法。
2.数学分析法——在球面与投影面之间建立点与点的函数关系,在平面上确定坐标网的一种投影方法。
实施投影时,①球面上一些经纬线的交点展绘在平面上;②对应连接经线和纬线,构成经纬网,球面上的点,按其经纬度转绘在平面上。
二、地图投影的基本概念地图投影原理证明,在一般情况下,椭球表面上无限小的圆圈投影到平面上为一椭圆,称之为变形椭圆(变形椭圆(ellipse of distortion ellipse of distortion ellipse of distortion))。
即,图形的比例尺不仅取决于点位,而且可能随着该点上方向的不同而变化。
因此,可分为主比例尺和局部比例尺。
主比例尺---等于地球椭球模型的比例尺。
局部比例尺---是作为地图上无限短的线段与椭球面上相应线段之比值。
取地面上一个微分圆,将它投影后变为椭圆(除个别为正圆外,一般皆为椭圆),通过研究其在投影平面上的变化,作为地图投影变形的几何解释,这样的椭圆称为变形椭圆(TissotTissot’’s indicatrix 蒂索指线)。
只要有投影就会产生变形;对某一地图投影来讲,不存在这种变形,就一定存在另一种或两种变形。
人们只有掌握地图投影变形性质和规律,才能有目的地支配和控制地图投影的变形。
§2 地图投影的变形Tissot’’s TheoremTissot一、长度变形二、角度变形三、面积变形四、等变形线M.A. Tissot’s Theorem定律底索法国数学家无论采用何种转换方法,球面上每一点至少有一对正交方向线,在投影平面上仍能保持其正交关系。
地图投影基本理论

1.长度比的基本公式 2.投影的三种条件
第一节 地图投影的概念与若干定义
地球表面的经纬线网格与平面建立了相互对应的网格的数学 关系时,则地球表面各该网格内的要素也能满足这种数学法则而 被表示在平面上。
地图投影:利用一定的数学法则把地球表面上的经纬线网表示 到平面上。
主要内容:研究把曲面表示到平面所采用的各种数学法则。 如果地球表面上有一点A (φ,λ),它在平面上的对应点是A′(x, y),此两点坐标之间可用下列函数关系式表示:
(1)
它随点的位置(经纬度)、方位角而变化。
当α=0°或α=90°时,即为 m E
M
n G r
引入m、n,(1)式也可表示为:
EG m n M r
•主方向与极值长度比
将(1)式对α求一阶导数,并设在α= α0时有极值
d 2 d
E M2
sin 20
G r2
sin 20
2F Mr
cos 20
0
化简后有:
tan 20
2F Mr
E M2
G r2
或 tan
2
=2mn
0
m2
cos
n2
考虑正切函数周期,上式有二解:2α0及2α0+180。对应 极值长度比的方向有α0及α0+90。
结论:极值长度比在椭球体表面处于两个互相垂直的方向上。 称这两个特殊的方向为主方向。
sin ' sin(n m )
1 EG
x
y
x
y
第03章 地图投影
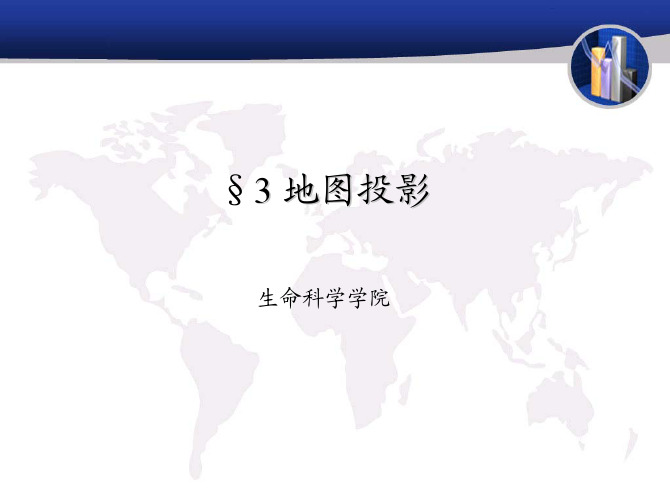
⑵ 不同变形性质投影的变形分布
⑶应用范围 • 根据圆柱投影的变形规律和经纬网的特点,在赤道附近沿 东西方向延伸地区的地图,最适宜采用各种变形性质的圆 柱投影; • 全球区域的地图可采用等角或等距圆柱投影,航海和航空 图上常常采用墨卡托投影; • 由于圆柱投影的经线为平行直线,便于显示时区的划分, 因此它也是世界时区图的主要投影。
⑵条件投影 • 根据某些条件,用数学解析法确定球面与平面之间点与点的 函数关系。 • 伪方位投影:在方位投影的基础上,根据某些条件改变经线 形状而成,除中央经线为直线外,其余均投影为对称中央经 线的曲线。 • 伪圆柱投影:在圆柱投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 伪圆锥投影:在圆锥投影基础上,根据某些条件改变经线形 状而成,无等角投影。除中央经线为直线外,其余均投影为 对称中央经线的曲线。 • 多圆锥投影:设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在中央经线 的延长线上。中央经线为直线,其余经线投影为对称于中央 经线的曲线。
§3 地图投影
生命科学学院
§1. 常用的地图坐标系
• 1.1 平面直角坐标系
x,y
• 1.2 平面极坐标系
ρ,δ
• 1.3 平面直角坐标与极坐标的关系
x q cos y sin
§2. 地图投影的基本概念
• 2.1 地图投影的定义
为什么要进行地图投影?
2
ab ab
当投影后经纬线正交,即θ=90°时:
,b n ; P ab mn ;
a m
sin
2
(地图学课件)第2讲链接(第三章我国地形图采用的地图投影)
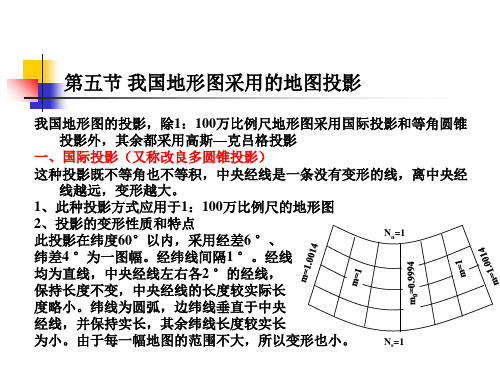
此投影在纬度60°以内,采用经差6 °、
Nn=1
纬差4 °为一图幅。经纬线间隔1 °。经线
均为直线,中央经线左右各2 °的经线,
保持长度不变,中央经线的长度较实际长
度略小。纬线为圆弧,边纬线垂直于中央
经线,并保持实长,其余纬线长度较实长
为小。由于每一幅地图的范围不大,所以变形也小。 Ns=1
第五节 我国地形图采用的地图投影
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 5、对多圆锥投影原理的解释 多圆锥投影,中央经线投影为直线且保持长度不变,其余经线投影为对
称于中央经线的曲线;赤道投影为直线,其余纬线投影为同轴圆弧, 圆心位于中央经线上,各纬线投影后保持长度不变且与中央经线正 交。
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥 投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影) 3、拼接时产生的后果 由于各幅地图均系单独投影,虽然同一列与同一行图幅可以密切拼接,
但上下左右四幅拼接在一起,则发生裂隙。如果九幅或更多幅地图 拼接在一起,则变形更大,但仍可有效的进行研究地区的阅读。 4、七十年代以前,我国1/100万地图一直采用国际投影,现在改用等角 圆锥投影。
第五节 我国地形图采用的地图投影
我国地形图的投影,除1:100万比例尺地形图采用国际投影和等角圆锥
投影外,其余都采用高斯—克吕格投影
一、国际投影(又称改良多圆锥投影)
这种投影既不等角也不等积,中央经线是一条没有变形的线,离中央经
线越远,变形越大。
1、此种投影方式应用于1:100万比例尺的地形图
地图投影知识点总结

地图投影知识点总结地图投影是将三维地球表面映射到二维平面上的过程。
由于地球是一个三维的球体,而地图是一个二维平面,因此无法完美地将地球表面映射到地图上。
地图投影是一项复杂的工程,需要考虑到地球的形状、尺寸、方向和角度等因素,以及地球表面的曲率和变形等问题。
地图投影有很多种类,每种投影方法都有其优点和局限性。
以下是地图投影的一些基本知识点总结:地图投影的分类:地图投影可分为等距投影、等角投影和等面积投影。
等距投影是指保持地球表面上任意两点之间的距离比例不变,但方向可能会发生变化。
等角投影是指保持地球表面上任意两点之间的夹角不变,但距离和面积可能会发生变化。
等面积投影是指保持地球表面上任意两个区域的面积比例不变,但方向和角度可能会发生变化。
根据投影面的形状,地图投影可分为圆柱投影、圆锥投影和平面投影。
地图投影的选择:选择适合的地图投影方法需要考虑到所要表达的地理信息、地图的使用目的和范围等因素。
例如,对于航海、航空和导航等领域,需要选用等角投影;而对于地图的变形要求较小的地理信息分析和遥感影像处理等领域,适合使用等面积投影。
地图投影的变形:地图投影会造成三种类型的变形:形状变形、大小变形和方向变形。
形状变形是指地球表面上的形状在地图上可能发生拉伸或压缩;大小变形是指地球表面上的面积在地图上可能会发生增加或减小;方向变形是指地球表面上的方向在地图上可能会发生偏差。
地图投影方法的选择要考虑到这些变形问题,以减小变形的影响。
常见的地图投影方法:1. 麦卡托投影:是一种圆柱形等距投影,常用于世界地图,保持了纬线和经线的直角,但是南北两极地区的变形严重。
2. 鲍尔投影:是一种圆柱形等面积投影,保持了地区间的面积比例,但是形状变形较大。
3. 兰伯特等角投影:是一种圆锥形等角投影,保持了地区间的角度比例,但是大小和形状变形较大。
4. 鲁宾逊投影:是一种混合投影,综合了以上投影方法的优点,常用于世界地图,尽量减小了地图的变形。
地图投影基础知识知识讲解

一、地图投影的基本问题 二、常见地图投影 三、地图投影的选择与辨认
一、地图投影的基本问题
1 地图投影的概念
地图投影就是在球面与平面之间建立其 经纬度与直角坐标函数关系的数学方法
2 地图投影的变形 3 地图投影的分类 4 地图投影的命名 5 GIS中地图投影的选择与判别
1 地图投影的概念
• 数学上的投影 面1
高斯—克吕格投影 (Gauss-Kruger Projection)
横轴圆柱投影
x y
高斯-克吕格投影原理图
高斯—克吕格投影 (Gauss-Kruger Projection)
高斯投影特征: 中央经线和赤道投影为互相垂直的直线,且为投影 的对称轴 投影后无角度变形,即保角投影 中央经线无长度变形 同一条经线上,纬度越低,变形越大,赤道处最大 同一条纬线上,离中央经线越远,变形越大; 为了保证地图的精度,采用分带投影方法,即将投 影范围的东西界加以限制,使其变形不超过一定的限 度,这样把许多带结合起来,可成为整个区域的投影 在6°带范围内,长度变形线最大不超过0.14%
长度变形、面积变形、角度变形
地图投影变形的图解示例 (摩尔维特投影-等积伪圆柱投影)
长度变形
角度变形
地图投影变形的图解示例
(UTM-横轴等角割圆柱投影)
面积变形和长度变形
投影变形示意图
地图投影——地图投影的变形
地图投影的变形示意
3 地图投影的分类
按承影面的形状分为:方位投影(平面 投影)、圆锥投影Байду номын сангаас园柱投影
空间斜轴墨卡托(SOM)投影
• 该投影是美国针对陆地卫星对地面扫描 图像的需要设计的一种近似等角性质的 投影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
33
(3)等距离投影条件
等距离投影:只在某个特定方向上长度没有变形。 规定经线长度比为1。
m 1
34
等距离投影只在某些特定方向上没有 变形。多用于对投影变形没有特殊要求的 地图,如教学地图。
35
课堂小结
地图投影方程:地图投影的基础 变形:长度、角度、面积
29
(1)等角投影条件
在投影平面上任何一处两方向所夹之 角都无变形, 即最大角度变形为零,长度 比相等。
0
sin a b
2 ab
ab
30
等角投影在微小区域内,图上的图形与实 地是相似的,又叫相似投影或正形投影,其 面积变形比别的投影大。
等角投影在图上量测方向和距离比较方便,世 界各国地形图多用此投影。
dS
dS
ds2 dx2 dy2 dx xBdB xLdL,
x f1B, L y f2B, L
dy y BdB yLdL
ds 2 M 2dB 2 L2dL2
2
EdB2 2FdBdL GdL2 M 2dB 2 L2dL2
tg DC
AD
2 E cos2 F sin 2 G sin 2
13
3、角度变形
u
u
角度变形公式:
角度变形也是一个变量,它随点位的变化而变化。
变形越小越好 局部点、线不变形
14
投影平面切在某点,该点在球面上,也在投影 平面上,这样的点投影后不产生任何变形。
圆锥与地球某纬线圈相切,圆柱在赤道上与地 球相切,这些相切的纬线投影后均无变形。在地 图投影中不变形的纬线称之为标准纬线。
8
2.2 地图投影变形
由球面向平面投影时引起的点、线、面的变化。
长度变形 角度变形 面积变形
9
1、长度比与长度变形
原面与投影面微分关系
长度比公式:
dS
dS
长度变形公式: 1
10
dS
dS
1
0 投影后长度增加了;
0 投影后长度缩短了;
0 无长度变形。
长度比是一个变量,随点位不同而变化,在 同一点上随方向变化而变化。
变形无时不在! 地图投影变形条件:为建立适宜的 地图投影提供理论基础。
x f1(B, L) y f2(B, L)
地图投影的标准纬线 15
2.3 主方向和变形椭圆
(1)主方向
C
A
O
B
D
正交方向
C′
A′
O′
B′ D′
不正交方向
16
总有一组互相正交的方向投影后仍
然正交,称此二方向为主方向。
C
A
O
B
D
C′
A′
O′
B′
D′
17
(2)变形椭圆
ξ
D
C
1
AB
η
球面
ξ′
D ′ C′
A ′ B′
η′
投影面
地球面上一无穷小的圆投影在平面上一般为无穷 小的椭圆。
3
2.1 地图投影一般方程
实质:将地球椭球面上的点映射到平面上点.
B , L x,y
地图投影
4
地图投影的一般方程:
x f1B, L y f2B, L
或
x f1, y f2 ,
椭球体 球体
5
一般方程
x f1B, L y f2B, L
地球椭球面上的点映射到平面上点:
一一对应
f1,f2 : 取决于不同的投影条件
经纬线夹角计算公式:
tg H
F
sin H
EG 经纬线夹角变形:
2
27
最大角度变形计算公式:
sin a b
2 ab
tgΒιβλιοθήκη ab2 2 abtg(
)
a
44 b
tg( ) b
44 a
a, b极值长度比
28
2.5 地图投影条件
(1)等角投影条件 (2)等面积投影条件 (3)等距离投影条件
南京师范大学地理科学学院GIS系
地图学
Cartography
第三章 地图投影原理及方位投影
第2讲 地图投影基本理论
回顾 地图投影
实质:将地球椭球面上点投影到平面上点。
地球椭球面
B,L
x,y
地图平面
地图投影
2
内容
2 地图投影的基本理论
2.1 地图投影一般方程 2.2 地图投影变形 2.3 主方向和变形椭圆 2.4 投影变形计算 2.5 地图投影条件
椭圆是由投影变形而产生:变形椭圆。
18
(3)沿主方向变形椭圆
x
C
1
A
y
x′
a C′
A′ b
y′
主方向具有两个重要性质: • 投影后仍然保持正交
• 主方向具有最大长度比a和最小长度比b
19
(4)变形椭圆的应用
• 表示一点的
变形
• 扁平程度反
映角度变形大 小
• 一组变形椭
圆反映全区域 变形情况
20
2.4 地图投影变形计算
(1)长度比计算公式 (2)面积比计算公式 (3)角度变形的计算
21
22
投影一般方程: x f1B, L y f2B, L
第一基本量:
E
x
2
y
2
B B
F x x y y B L B L
G
x
2
y
2
L L
H x y y x B L B L
23
(1)长度比计算公式
任何一种投影都存在长度变形。
11
2、面积比与面积变形
dF
面积变形公式:
dF
面积比公式:
P dF dF
面积变形公式: p P 1
12
P dF dF
p P 1
p 0 ,表示投影后面积增大; p 0 ,表示投影后面积缩小; p 0 ,表示面积无变形。
面积比或面积变形也是一个变量,随点 位的变化而变化。
单值、连续、有界
6
特殊情况
若经度为常数L0,则经线投影方程为:
x f1B, L0 y f2 B, L0
若纬度为常数B0,则纬线投影方程为:
x f1B0 , L y f2 B0 , L
7
若消去纬度B, 经线族投影方程:
F1( x, y, L) 0
若消去经度L, 纬线族投影方程:
F2 ( x, y, B) 0
M2
Mr
r2
24
0,沿经线方向长度比计算公式:
m E M
900 ,沿纬线方向长度比计算公式:
n G r
25
(2)面积比计算公式
P dF dF
dF AD • AB MrdBdL
dF AD • AB • sin m nM r sin dBdL P m n sin
26
(3)角度变形的计算
我国大中比例尺地形图上所采用的高斯—克吕 格投影就是等角横切椭圆柱投影。
小比例尺地形图和航空图则采用等角圆锥投影。
31
(2)等面积投影条件
等面积投影:在投影平面上保持面积大小 与椭球面上相应的面积一致,即面积变形为零。
P 1 ab 1 H Mr
32
等面积投影改变原来的形状,破坏 了图形的相似性,其角度变形一般比别 的投影大。
