初中物理竞赛教程 光学中的成像问题
上海初中物理竞赛光学板块(10)光具组成像

上海初中物理竞赛汇编:光具组成像一、单项选择题1、一束平行于凸透镜L1主光轴的平行光经过透镜会聚焦到焦点。
现在L1的右侧一倍焦距内某位置放置一障碍物P,且与主光轴垂直,其中心有一个直径的d1的圆孔,圆心位于主光轴上,如图所示,在障碍物的右侧,距离障碍物S出垂直主光轴放置一个光屏(图中未画出),屏上出现了一个直径为d2的圆形光板。
若在障碍物圆孔出嵌入一块薄凹透镜L2,屏上恰好出现一个亮点,已知S=10cm,d1=1cm,d2=0.5cm,则凹透镜L2的焦距大小为( )A.30cm B.25cm C.20cm D.15cm2、如图所示,两平面镜AM,AN之间的夹角为90°,凸透镜的主光轴恰好是该直角的角平分线,凸透镜的光心为O,A点恰好是凸透镜的焦点,光源S位于主光轴上,通过该系统,光源S所成的像为()A.四个虚像,三个实像B.四个虚像,一个实像C.三个虚像,一个实像D.三个虚像,两个实像3、如图所示,平面镜水平放置且镜面朝上,在镜面上方竖直放置一凸透镜,在凸透镜左侧主光轴上两倍焦距处有一点光源S,关于点光源在该光具组中成像情况的判断,正确的是()A.两个实像,两个虚像B.两个实像,一个虚像C.一个实像,两个虚像D.一个实像,三个虚像4、如图所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体AB,在透镜右侧三倍焦距处竖直放置一平面镜MN,镜面与凸透镜的主光轴垂直,B、N两点都在主光轴上,AB与MN高度相等,且与透镜上半部分等高.遮住透镜的下半部分,则该光具组中,物体AB的成像情况是()A.两个实像,一个虚像B.一个实像,两个虚像C.只有一个虚像D.只有一个实像5、如图所示,在光具座上自左向右依次竖直放置一个凹透镜、凸透镜和平面镜,两个透镜的主光轴重合,凸透镜的焦距为f,此时两个透镜之间的距离为L.在凹透镜的左侧有一水平平行光束通过两个透镜后入射到平面镜上,经平面镜反射后,反射光恰能沿原来的光路返回,据此可判断凹透镜的焦距为()A.f B.L C.f+L D.f﹣L6、如图所示,凸透镜的下半部分被截去,其上半部分的高度为L.在其左焦点F处放有高为L的发光物AB,在右焦点F',处放有一平面镜MN.则关于AB通过凸透镜的成像情况,下列说法中正确的是()A.成一个正立等大的虚像和一个正立放大的虚像B.成一个正立等大的虚像和一个倒立缩小的实像C.AB的上半部分成一个等大倒立的实像,下半部分不成像D.AB的下半部分成一个等大倒立的实像,上半部分不成像7、如图所示,凸透镜的焦距为5厘米,在透镜左侧10厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB的成像情况是()A.一个正立实像,一个倒立实像,一个正立虚像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个倒立实像,一个正立虚像,一个倒立虚像D.一个正立实像,一个倒立实像,一个倒立虚像8、如图所示,平面镜OM与ON垂直放置,在它们的角平分线上P点处,放有一个球形放光物体,左半部分为浅色,右半部分为深色,在P点左侧较远的地方放有一架照相机,不考虑照相机本身在镜中的成像情况,则拍出照片的示意图正确的是()9、如图所示,平面镜和凸透镜的主光轴垂直并处在凸透镜两倍焦距处,在凸透镜另一侧两倍焦距处有一个点光源S.现将平面镜向凸透镜靠近的过程中,关于点光源所成的像,下述结论中错误的是()A.平面镜在移动过程中,最多只能成两个实像B.平面镜移动到一定位置时,正好只成一个实像C.平面镜移动到一定位置时,正好只成一个虚像D.平面镜移动到一定位置时,正好既成一个实像,又成一个虚像10、某人决定自己给自己照一张手拿相机拍照的像,他想了一个好主意,对着穿衣镜照相,当他距镜面2米时正准备按下快门,突然为调焦犯起愁来,你能告诉他把相机的距离标志调到()A.2米B.略大于2米C.4米D.略小于4米11、如图所示,在凸透镜的两个焦点处,垂直光轴放置两个大小相同的平面镜,镜面相对.每个平面镜都关于凸透镜的光轴上下对称.现在左侧平面镜的中心处挖去一个圆孔,在凸透镜左侧两倍焦距处一个点光源,则点光源在该光具组中所成的虚象个数为()A.一个虚像B.两个虚像C.无数虚像D.一个虚像也没有12、如图所示,当用眼睛去观察镜子时,光束似乎是从M处发散开来的,则透镜的焦距是()A.0.1m B.0.2m C.0.3m D.0.5m13、在凸透镜主轴上的一物点P,物距大于焦距,如果沿直径对称切除透镜很小一部分,如图所示,再把上、下半截透镜向原主轴位置合拢,则成像情况与原来相比()A.相同B.成两个像,上半截透镜A成像点上移,下半截透镜B成像点下移C.成两个像,上半截透镜A成像点下移,下半截透镜B成像点上移D.不能成像14、如图所示,在直角坐标系原点O处放置平面镜MN,它与坐标轴x呈45°.在O点正下方(S=15厘米)处水平放置一焦距为10厘米凸透镜.A为一点光源,则关于凸透镜所成的像正确的是()A.在凸透镜下方成一个实像,在凸透镜上方成一个虚像B.只在凸透镜下方成一个实像C.在凸透镜的下方、y轴的左右两侧各成一个实像,但左边的实像更靠近凸透镜D.在凸透镜的下方、y轴的左右两侧各成一个实像,但右边的实像更靠近凸透镜15、巨大的平面镜中嵌有一凸透镜,凸透镜主轴与平面镜垂直,一直立线状物体放在凸透镜右侧2倍焦距主轴上,一光屏放在凸透镜左侧2倍焦距处,如图所示.现用眼睛在物体右侧任一位置向左观察,可能看到的像应是图中的()16、一块凸透镜被剖成对称的两半,并按如图所示对接.一个物体ab置于凸透镜前3倍焦距处,则对凸透镜成像的描述中,有可能正确的是图中的()17、如图所示,图中画出了光通过焦距分别为f1和f2的两块透镜L1和L2前后的情况.下列对透镜L1、L2的种类和焦距的分析有可能正确的是()A.L1是凸透镜,L2是凹透镜,且f1>f2B.L1是凸透镜,L2是凹透镜,且f1<f2C.L1是凹透镜,L2是凸透镜,且f1>f2D.L1是凹透镜,L2是凸透镜,且f1<f218、有人用照相机对着平面镜拍照,想摄出平面镜内的人物,结果()A.他不会成功,因为平面镜里成的是虚像B.他能摄出平面镜里的人物,而且和照相机直接对着人物拍摄没有区别C.他能摄出平面镜里的人物,但照片的左右与实际相反D.他能摄出平面镜里的人物,但照片的上下、左右都与实际相反19、一个直立的物体放在凸透镜的两倍焦距处,物体的中点恰在透镜的光轴上,后来,透镜被一割为二,对称地拉开,两个半透镜间距离等于物体高度,如图所示.则此时光屏上的像应该是图中的()二、多项选择题20、如图所示,L1,L2是焦距均为f的两个相同的凸透镜,主光轴重合,相聚为f。
全国中学生物理竞赛真题汇编---光学 参考答案
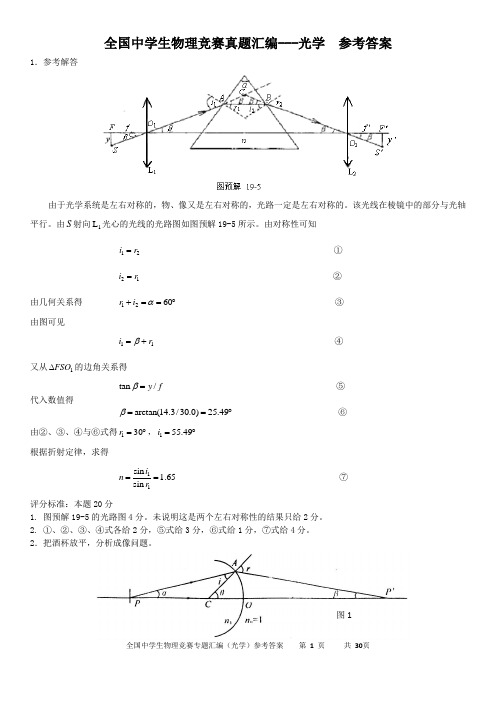
全国中学生物理竞赛真题汇编---光学 参考答案1.参考解答由于光学系统是左右对称的,物、像又是左右对称的,光路一定是左右对称的。
该光线在棱镜中的部分与光轴平行。
由S 射向1L 光心的光线的光路图如图预解19-5所示。
由对称性可知12i r = ①21i r = ②由几何关系得 1260r i α+==︒ ③ 由图可见11i r β=+ ④又从1FSO ∆的边角关系得tan /y f β= ⑤代入数值得arctan(14.3/30.0)25.49β==︒ ⑥由②、③、④与⑥式得130r =︒,155.49i =︒ 根据折射定律,求得11sin 1.65sin i n r == ⑦ 评分标准:本题20分1. 图预解19-5的光路图4分。
未说明这是两个左右对称性的结果只给2分。
2. ①、②、③、④式各给2分,⑤式给3分,⑥式给1分,⑦式给4分。
2.把酒杯放平,分析成像问题。
图11.未斟酒时,杯底凸球面的两侧介质的折射率分别为n 1和n 0=1。
在图1中,P 为画片中心,由P 发出经过球心C 的光线PO 经过顶点不变方向进入空气中;由P 发出的与PO 成α 角的另一光线PA 在A 处折射。
设A 处入射角为i ,折射角为r ,半径CA 与PO 的夹角为θ ,由折射定律和几何关系可得n 1sin i =n 0sin r (1) θ =i +α (2)在△PAC 中,由正弦定理,有sin sin R PCiα= (3) 考虑近轴光线成像,α、i 、r 都是小角度,则有1n r i n =(4) Ri PCα=(5) 由(2)、(4)、(5)式、n 0、n l 、R 的数值及 4.8PC PO CO =-=cm 可得θ =1.31i (6) r =1.56i (7)由(6)、(7)式有r >θ (8)由上式及图1可知,折射线将与PO 延长线相交于P ',P ' 即为P 点的实像.画面将成实像于P ' 处。
南师附中物理竞赛讲义104薄透镜成像.doc

10.4薄透镜成像一、薄透镜成像例1、设透镜由折射率n 的玻璃制成,放在空气中,两个球而的半径分别为|斤|和|引,透镜 厚度忽略不计。
对于近轴光线,在笛卡尔朋标规则下,(1)=s 、 s r x r 2(2) 透镜制造者公式:像方焦距:—=(/7-1)(-.厂 斤厂2⑶薄透镜成像公式:1-1=7(4)线放大率:加=匚注意:1、 以上公式的前提是(1)薄透镜⑵近轴光线成像(3) 两侧均为空气2、 以上公式对凸透镜和凹透镜均成立3、 不管透镜两边球面的半径人小,两侧的焦距人小一•定相等(要求两侧折射率相同)4、 物方是指入射光线所在的一方 物方蕉距:像方是指折射光线所在的一方思考:如果透镜两边不是空气,分别是折射率为山、血的介质,以上公式分别有什么变化?例2、如图所示,薄凹透镜L|和薄凸透镜L2共轴,放置在空气中,L]的焦距为20cm, L2 的焦距为10cm, L|和L2相距置10cm,物S在L】前方20cm处.试求像的位置和横向放大率.例3、透过焦距为0.30加的凸透镜观察在平静水面下0.04加的一条小鱼,若透镜在水面上方0.02/n ,观察者看到的鱼位于何处?假设鱼位于透镜的主光轴上,水的折射率为1.33例4、有一水平放置的平行平血玻璃板H ,厚3.0 cm,折射率M =1.5 o在其下表面F2.0 cm处有一小物S;在玻璃扳上方有一薄凸透镜厶,其焦距/ = 30cm,透镜的主轴与玻璃板面垂血;S位于透镜的主轴上,如图所示。
若透镜上方的观察者顺着主轴方向观察到S的像就在S处,问透镜与玻璃板上表面的距离为多少?(2)用计算法求出此像的位置和大小.例5、如图所示,折处放置射率n = 1.5的全反射棱镜上方0.06/n 处放置一个物体AB,棱镜 直角边长为0.06加,棱镜右侧0.10加一个焦距/, = 0.10m 的凸透镜,透镜右侧0.15加处再 放置一个焦距厶= -0.10加的凹透镜,求该光学系统最终成像的位置和像放大率。
上海初中物理竞赛汇编光学板块(9)成像公式 放大率 盲区

上海初中物理竞赛汇编:成像公式 放大率 盲区一、单项选择题1、点光源以速度v 做匀速直线运动,运动轨迹经过凸透镜两倍焦距处且与主光轴的夹角为θ(θ<45°),在点光源运动过程中,像相对点光源的最小速度为( )A .v sin θB .v cos θC .v sin2θD .v cos2θ2、F 为与点光源S 同侧的凸透镜焦点,S 所成的像为S',且SF 与SS'垂直。
SF =64mm ,SS'=27mm ,该凸透镜的焦距f 为( )A .6cmB .8cmC .10cmD .12cm3、如图所示,点光源位于凸透镜的主光轴上(途中未画出凸透镜的位置),当点光源位于A 点处,像成在B 点;当点光源位于B 点处,像成在C 点。
已知AB=5cm ,BC=10cm ,则凸透镜的焦距大小为( )A .1 cmB .5 cmC .30 cmD .60 cm4、凸透镜的焦距为f ,点光源为S 和光屏M 位于凸透镜的左右两侧,点光源位于凸透镜的主光轴上,光屏凸透镜的主光轴垂直并和点光源的距离保持L 不变,且f <L <4f 、左右移动凸透镜的位置,当光屏上的光斑最小时,凸透镜与点光源的距离为( )A .2L f + B .2L f - C D5、凸透镜的焦距大小为20cm,点光源位于透镜主光轴上距离光心30cm,现移动凸透镜,使点光源距离凸透镜100cm,该过程中,点光源的像移动的路程为()A.25cm B.35cm C.45cm D.55cm6、某人通过焦距为l2cm、直径为4cm的放大镜(薄凸透镜)看报纸,报纸与放大镜的距离为3cm,且与放大镜的主光轴垂直,保持放大镜的位置不变,眼睛始终位于主轴上且距离放大镜24cm位置处进行观测(不考虑眼睛的大小),报纸上有部分区域是“盲区”(即眼睛观测不到),该区域的面积为()A.9πcm2B.5πcm2C.3πcm2D.2πcm27、用凸透镜成像时,定义像与物的大小之比为“放大率”,则在物体成像的情况下()A.物距一定时,焦距越小放大率越大B.物距一定时,焦距越大放大率越大C.焦距一定时,物体离透镜越近放大率越大D.焦距一定时,物体离同侧焦点越近放大率越大8、如图所示,凸透镜竖直放置,凸透镜焦距f,现有一点光源S在凸透镜左侧以凸透镜两倍焦距处为圆心,在经过主光轴的竖直平面内做顺时针圆周运动,直径为D,且f<D<2f,则在下列关于点光源所成的像的运动轨迹的各图中,正确的是()二、多项选择题9、物体的高度为12cm,与凸透镜的主光轴垂直放置,经凸透镜成高度为6cm的缩小像。
全国初中物理竞赛试题精编(八年级上):第11讲—凸透镜成像规律专题精练(原卷版)

全国初中物理竞赛试题精编第11讲—凸透镜成像规律专题精练1.如图所示,1F、2F是凸透镜的两个焦点,S是距凸透镜前距离大于2倍焦距的点光源,S 是S经凸透镜所成的像。
当点光源S沿平行于主光轴方向向右匀速运动靠近透镜时,像S 的移动情况()A.像S 沿平行于主光轴方向靠近凸透镜方向匀速运动B.像S 沿O与S 连线方向远离凸透镜方向移动,速度逐渐变小C.像S 沿平行于主光轴方向远离凸透镜方向移动,速度逐渐变大D.像S 沿2F与S 连线方向远离平面镜方向移动,速度逐渐变大2.如图所示,为凸透镜成像的另一拓展规律在照相问题中的运用.即用可变焦距的光学照相机把远处的景物“拉近”进行拍摄,就是说,虽然被拍摄的物体与照相机镜头之间的距离基本不变,但仍可以使底片上所成的像变大.关于这个过程,下列说法中正确的是()A.焦距变大,像距也变大B.焦距变小,像距也变小C.焦距变大,像距变小D.焦距变小,像距变大3.小明同学在做凸透镜成像实验时,移动光屏,在光屏上呈现清晰放大的像,同时他也看到透镜表面有两个像,其中一个是正立的,一个是倒立的,对于透镜表面的两个像,下列说法正确的是()A.透镜表面的两个像,正立的是光的反射形成的,倒立的是光的折射形成的B.透镜表面的两个像,都是光照到透镜表面反射形成的虚像C.透镜表面的两个像,都是光照到透镜表面折射形成的实像D.透镜表面的两个像,倒立的是实像,正立的是虚像4.某种变焦镜头的变焦范围为15mm~85mm,用这个镜头对着远处的某一栋楼房拍照。
当使用焦距15mm 拍照时,显示屏上所成的清晰像的高度为h1;当使用焦距85mm拍照时,显示屏上所成的清晰像的高度为h2,则h1与h2的比值约为()A.3∶17B.17∶3C.289∶9D.9∶2895.物体的高度为12cm,与凸透镜的主光轴垂直放置,经凸透镜成高度为6cm的缩小像。
若将物体朝透镜方向靠近24cm,经凸透镜成高度为30cm的放大像,则此凸透镜的焦距大小可能为()A.10cm B.15cm C.20cm D.25cm6.在探究凸透镜成像规律的实验中,蜡烛、凸透镜、光屏的位置如图所示,烛焰恰好在光屏上成清晰的像,下列说法正确的是()A.该凸透镜的焦距是30cmB.换成焦距为10cm的凸透镜,在蜡烛和光屏不动的情况下,凸透镜从紧靠蜡烛向光屏移动,在光屏上可以得到两次清晰倒立的像C.在凸透镜左侧放一凹透镜,将光屏向右移动还能接收到清晰的像D.凸透镜与蜡烛不动,去掉光屏,人眼在100cm处能看到蜡烛的像7.某同学利用图示装置来研究凸透镜成像.(1)如图所示,当凸透镜位于光具座上A处时,恰好在光屏上成清晰的像,成的是________(正立/倒立)的像.蜡烛燃烧一段时间后,烛焰的像将位于光屏中心的________方;(2)在保持(1)中蜡烛和光屏位置不变的情况下,将凸透镜向右移到B处(图中未标出),光屏上再次成清晰的像,成的是________(选填“放大”、“缩小”或“等大”)的像;(3)在上述探究活动中,若已知蜡烛与光屏间的距离为L0,与凸透镜第一次所在位置A间的距离为L,如图所示,则该透镜焦距f________L(选填“>”、“<”或“=”),透镜先后两次所在位置A、B之间的距离S=________(用L0、L表示).(4)当光屏上呈现清晰的像时,保持发光体“F”和凸透镜位置不变,取一只与原实验中焦距相同但镜面直径较小的凸透镜,替代原来的凸透镜再次实验,所成的像与原来的像相比,你可观察到的现象有________.8.小明同学做“探究凸透镜成像规律”的实验,他根据收集的数据作出如图甲所示的图像:(1)由图像可知,小明同学使用的凸透镜的焦距为___________cm.(2)当蜡烛放置在光具座上的45cm刻度处时,小明应该如何观察烛焰的像?_________________________.(3)实验过程中,保持蜡烛和凸透镜的位置不变,调皮的明明把近视眼镜放在凸透镜和蜡烛之间,如图乙所示,小明发现光屏上烛焰的像变模糊了,此时他应该把光屏向_______(选填“靠近”或“远离”)透镜的方向移动,才能得到清晰的烛焰的像.9.学习小组用图甲所示的圆柱形纸质套筒做“探究小孔成像规律”的实验,发现像的大小不同,亮度也不一样。
物理竞赛 第6讲.近轴成像.教师版

1. 折射定律近似计算2. 折射成像问题知识点拨一:近轴折射光线近似计算原理 引入:视深视高问题学过光学的人都知道的基本常识,我们从水面看水中的鱼,看到的像要比实际深度浅,那么具体值是多少呢?不妨研究一下:如图所示,一个物点位于折射率为n 的媒质中h 0深处,当在媒质界面正上方观察时,物体的视深为:h=nh 0。
证:根据光路可逆和折射定律:n=risin sin 一般瞳孔的线度d=2~3毫米,因此i 和r 都非常小,则sini ≈tani=ha ,sinr ≈tanr=0h a。
故有n=r isin sin =hh 0可见:视深比实深小。
反过来:如果从折射率为n 的媒质中,观察正上方距液面高为h 0的物点,则视高为h=nh 0。
当然,以上的结论并不具有普遍意义,都谈不上是公式。
但是推导的过程给了我们一些提示,对于近轴的光线,入射角度和折射角度都是非常小的,所以我们在使用折射定律的时候不妨“无赖”一点,根据数学计算的方便把正弦,正切,弧度角随意互换使用,我们还会经常使用正弦定理,把角的正弦比等效为边长之比。
给一些定义后,我们来导一个有指导意义的公式。
几个重要概念:①像与物的概念:发光物体上的每个发光点可视为一个“物点”即“物”。
一个物点上发出的光束,经一系列光学系统作用后,若成为会聚光束,则会聚点为物的实像点;若成为发散光束,则其反向延长线交点为物的虚像点;若为平行光束则不成像。
②实物与虚物:发散的入射光束的顶点(不问是否有实际光束通过此顶点)是实物;会聚的入射光束的顶知识体系介绍第6讲 近轴成像点(永远没有实际光束通过该顶点)是虚物。
③焦点与焦距:平行光线射向光学器件后,实际汇聚的点叫实焦点,反向延长汇聚的点叫虚焦点。
光具到焦点的距离叫焦距。
焦距可以看成无穷远的实物对光具成像的相距。
例题精讲【例1】在一个曲率半径为R 的左右两侧面各有折射率为n 1, n 2的两种透明介质,证明球介面折射的成像公式为:Rn n v n u n 1)(2121-=+。
初中物理竞赛及自主招生专题讲义第四讲光现象初步第二节平面镜成像含解析

第二节平面镜成像一、平面镜的成像规律平面镜所成的像是正立的虚像,像与物大小相等,像与物到镜面的距离相等且像与物的连线与镜面垂直.亦即像与物关于镜面对称.物体发出的光线经过平面镜反射后,反射光线的反向延长线在镜后会聚为虚像,如图2.37所示。
当我们在镜前时,经过平面镜反射后进入人眼的光线看起来好像是从镜后的虚像S 发出的。
二、平面镜的典型问题(一)根据光路的可逆性确定平面镜观察范围的光路图观察者不动,通过平面镜能看到物体的范围是多大?对这一问题常应用光路可逆性原理,把眼睛看做“发光体”,眼睛发出的光照亮的区域即为能看到的区域。
例1 如图2。
38所示,某人躺在地板上,眼的位置在A处.一只小虫在地板上从右向左爬,从天花板上的平面镜MN看到小虫的像,问小虫爬到何处时,人在平面镜中就看不到小虫了?请画图说明。
分析与解假设人眼为一光源,它的像为A'.人眼“发出”的光照射到平面镜上后,反射出的光照亮地板的区域为S S,注意画12光路图时要按光实际传播的方向加上箭头。
如图2.39所示,S S区域发出的光经平面镜反射后12可到达A点,即A处的眼睛可通过平面镜看到S S区域的小虫的像,当小虫爬到12S S区域以外12时,就不能通过平面镜看到它的像了。
例2 (第22届全国预赛试题)内表面只反射而不吸收光的圆筒内有一半径为R的黑球,距球心为2R处有一点光源S,球心O和光源S皆在圆筒轴线上,如图2。
40所示。
若使点光源向右半边发出的光最后全被黑球吸收,筒的内半径r最大为多少?分析与解当光源S发出的光线经圆筒内表面反射后,反射光线全部被球接收,则点光源向右半边发出的光最后全被黑球吸收。
自光源S作球的切线SM,并画出S经筒壁反射形成的虚像点S',从S'画出球面的切线S N',如图2。
41(a)所示。
可以看出,只要S M'和S N'之间有一夹角,则从简壁上反射的光线就有一部分进入球的右方,不会完全落在球上被吸收。
初中物理竞赛中“光学”的辅导技巧

物理竞赛中“光学”的辅导技巧《光学》一章,初中的要求是较基础的.它主要是运用一些基本原理和规律去解释常见的光学现象和应用由于物理竞赛的层次相应提高,因而在辅导时有必要拓展学生的知识面,开阔其视野并发展能力.那么应如何进行辅导呢?笔者有如下体验:1.利用光路图化抽象为形象,总结规律并予以运用.光路图是驾御光学知识的翅膀,借助它可以透过知识的幻像,将某些抽象的光学知识抽丝剥茧,从而剖析得到规律性的知识并用它解释有关的现象.对于“凸透镜成像”一节,我有如下的运用:2.(1) 根据“平行于主光轴的光线折射后会聚于焦点,透过光心的光线方向不变”的规律,我引导学生画出u>2f时成像光路图(如图1),由图可见其得到倒立、缩小的实像(顺延光线ab和cd可相交的为实像,反向延长相交的为虚像),其像距为 f<v<2f,同理可引导学生分析得到f<u<2f的规律.此外,根据作图法,可分析 98年竞赛中的一道选择题:3.老奶奶看报时,为了看到更大的清晰的像,她常选择做()A.报与放大镜不动,眼睛离报远一些;B.报与眼不动,放大镜离报远一些;C.报与放大镜不动,眼睛离报近一些;D.报与眼不动,放大镜离报近一些.作图时(图2),由于字的大小不变,故反向延长后分别得到虚像A‘B’和C‘D’,由图可见字AB 离透镜远一些,其像A‘B’也大一些,故选(B)?(2)对变焦相机的解释.所谓变焦相机,是指通过改变相机的焦距来改变像的大小.例如“体育记者要在较远处拍摄较大的清晰的像,则其焦距应如何调整?”对于这类问题先要引导分析其异同点:如图3,物体ab 大小相同但焦距不同,由图可见焦距长的所成的像ef较大,故体育记者拍摄远景时一般要使用“大炮筒”.2。
以实验为阶梯,引导学生登上更高境界,并激发其求知欲和培养学生手、脑并用的能力.物理是一门以实验为基础的应用学科,通过实验可进一步印证和拓展课本知识,培养学生的兴趣和勇于探求真知的精神,而“尖子生”动手、动脑能力更强,为了尽展学生的一技之长,老师在辅导时应尽可能开放各种实验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理竞赛教程浅谈光学中的成像问题光在同一种均匀介质中传播时遵循光的直线传播规律,若从一种介质进入另一种介质,在其介面上要同时发生反射与折射现象,其光线分别遵循光的反射定律与光的折射定律,这就是几何光学的三大传播规律。
在高中物理竞赛辅导的过程中,经常会遇到有关物体成像问题。
光学中的成像问题可归结为两类:一类是反射成像,也就是反射光直接相交成像(实像),或反射光延长线相交成像(虚像 );另一类是折射成像,也就是折射光直接相交成像(实像),或折射光延长线相交成像(虚像 )。
现将光学竞赛中涉及的成像问题作一归类分析.一、 反射镜与反射成像反射镜遵循光的反射定律,如果反射面是平的我们就称是平面镜,如果反射面是球面的一部分,这种镜叫球面镜。
反射面如果是凹面的叫凹面镜,简称凹镜;反射面是凸面的叫凸面镜,简称凸镜。
它们有共同的成像规律: 成像公式:f v u 111=+=R2(R 为球面镜的曲率半径) 像的长度放大率:uv f u f AB B A m =-==11 这些公式只适用于近轴光线成像。
u 、v 的符号法则与透镜类似,即实物u 为正值,虚物u 为负值;实像v 为正值,虚像v 为负值;凹镜的焦距f>0,凸镜的焦距f<0。
而对于平面镜可看作是球面镜的一个特例,即曲率半径R=∞。
这样,我们可得到平面镜成像的简单公式:1,=-=m u v二、 折射镜与折射成像棱镜与透镜的成像规律遵循光的折射定律,属于折射镜。
这里只谈薄透镜成像的规律。
薄透镜是一种理想化的物理模型,它们两表面的曲率中心之间的距离大于它两个顶点之间的距离。
对近轴光线,其成像规律与球面镜相似。
成像公式:fv u 111=+ 其中透镜的焦距)11)(1(121r r n f +-= (1r 、2r 是二球面的半径,n 是透镜的折射率) 像的长度放大率:uv f u f AB B A m =-==11 u 、v 的符号法则:实物u 为正值,虚物u 为负值;实像v 为正值,虚像v 为负值;凸透镜的焦距f>0,凹透镜的焦距f<0。
三、 光具组成像各个光学元件组成的光光系统称为光具组。
解物体通过光具组成像这类问题的总原则是:物体通过前一光学元件所成的像就是后一光学元件的物,遇到平面镜、球面镜等反射镜,就考虑光线折回后再成像这一点。
具体地说,可有以下几个结论:1、后一次成像的物距(有正负)等于前后两光具的距离(总为正)与前一次成像的像距(有正负)之差,即n n n v d u -=+12、最终成像位置由最后一个光具所成像的位置决定。
0>n v 表示最终成像在最后光具沿主轴的正向侧,0<n v 表示最终成像在最后光具的反向侧。
3、最终成像的虚实,由最后一次成像决定,0>n v 为实像,0<n v 为虚像。
4、总放大系数等于各次放大系数的乘积,即 321m m m m =5、最后成像正倒的确定:先根据单次成像时,实物成实像与虚物成虚像为倒立,实物成虚像与虚物成实像为正立的原则确定正、倒立的总次数,再根据倒立了偶数次则最终成像正立、倒立了奇数次则最终成像倒立确定最终成像的正倒情况。
如果各光学元件之间的距离0=d ,那么整个光具组的总焦距f 与各个光学元件的焦距f 1、f 2、f 3之间存在如下的关系: +++=3211111f f f f 。
我们就可应用整个光具组成像法解决成像问题。
四、 应用举例例1:一平行光沿薄平凸透镜的主光轴入射,经透镜折射会聚于透镜后f=48cm 处,透镜的折射率为n=1.5。
若将此透镜的凸面镀银,物置于平面前12cm 处,求最后所成像的位置。
分析与求解:根据透镜的焦距公式)11)(1(121r r n f +-=, 而r 1=∞,21)1(1r n f -= 解得凸球面的半径r 2=24cm. 凸面镀银后,相当于有三个光学元件组合成像,即先通过透镜折射成像,再经球面镜反射成像,最后再经透镜折射成像。
先经透镜成像111111v u f +=,得cm v 161-= 再经凹面镜成像cm u 162=,22222111r f v u ==+ 得cm v 482=最后又经透镜成像cm u 483-= ,331111v u f +=,cm v 243=。
即最后成像在透镜前24cm 处。
此题还有另外一种解法。
由于三个光学元件之间的间距为0,设整个光学系统的总焦距为f,则有3211111f f f f ++=,得光具的总焦距为f=8cm.再由成像公式f v u 111=+,811121=+v ,得cm v 24= 例2:在焦距为15cm 的会聚透镜左方30cm 处放一物体,在透镜右侧放一垂直于主轴的平面镜,试求平面镜在什么位置,才能使物体通过此系统所成的像距离透镜30cm?分析与求解:设平面镜与透镜的距离为d,物距cm u 301=,焦距cm f 151=111111v u f +=, 得cm v 301=。
由平面镜成像时cm d u )30(2-=,cm d v )30(2-=最后又经透镜成像,cm d v d u )302(23-=-=331111v u f += 解得452)302(153--=d d v 若成实像cm v 303=, 此时d=30cm若成虚像cm v 303-=, 此时d=20cm例3:设有两个薄凸透镜o 1和o 2,其焦距分别为f 1=20cm,f 2=30cm,两者共轴,相距d=35cm,在主光轴上透镜o 1左方100cm 处垂直于主轴放一长为4cm 的物体,求最终成像的位置、大小和虚实情况。
分析与求解:物体先经透镜o 1成像,物距cm u 1001=,焦距cm f 201= 由111111v u f +=, 得cm v 251=。
放大率25.0211==u v m再经透镜O 2成像,cm cm d u 10)25(2=-=,焦距cm f 302= 由222111v u f +=,得cm v 152-=。
放大率5.1222==u v m 最终成像的总放大率375.021==m m m ,像长为1.5cm 倒立的虚像,像在透镜O 2左方15cm 处。
例4、一平凸透镜焦距为f,其平面上镀了银,现在其凸面一侧距它2f 处,垂直于主轴放置一高为H的物,其下端在透镜的主轴上。
1、用作图法画出物经镀银透镜所成的像,并标明该像是虚、是实。
2、用计算法求出此像的位置和大小。
分析与求解:1. 用作图法求得物AP ,的像''A P 及所用各条光线的光路如图预解16-5所示。
说明:平凸薄透镜平面上镀银后构成一个由会聚透镜L 和与它密接的平面镜M 的组合LM ,如图所示.图中O 为L 的光心,'AOF 为主轴,F 和'F 为L 的两个焦点,AP 为物,作图时利用了下列三条特征光线:(1)由P 射向O 的入射光线,它通过O 后方向不变,沿原方向射向平面镜M ,然后被M 反射,反射光线与主轴的夹角等于入射角,均为α。
反射线射入透镜时通过光心O ,故由透镜射出时方向与上述反射线相同,即图中的'OP .(2)由P 发出已通过L 左方焦点F 的入射光线PFR ,它经过L 折射后的出射线与主轴平行,垂直射向平面镜M ,然后被M 反射,反射光线平行于L 的主轴,并向左射入L ,经L 折射后的出射线通过焦点F ,即为图中的RFP .(3)由P 发出的平行于主轴的入射光线PQ ,它经过L 折射后的出射线将射向L 的焦点'F ,即沿图中的'QF 方向射向平面镜,然后被M 反射,反射线指向与'F 对称的F 点,即沿QF 方向。
此反射线经L 折射后的出射线可用下法画出:通过O 作平行于QF 的辅助线'S OS ,'S OS 通过光心,其方向保持不变,与焦面相交于T 点,由于入射平行光线经透镜后相交于焦面上的同一点,故QF 经L 折射后的出射线也通过T 点,图中的QT 即为QF 经L 折射后的出射光线。
上列三条出射光线的交点'P 即为LM 组合所成的P 点的像,对应的'A 即A 的像点.由图可判明,像''A P 是倒立实像,只要采取此三条光线中任意两条即可得''A P ,即为正确的解答。
2.计算物AP 经LM 组合所成像的位置、大小。
解法一:按光具组整个系统成像计算像的位置和大小。
由于三个光学元件之间的间距为0,设整个光学系统的总焦距为总f 。
这三个光学元件分别是两个透镜和一个平面镜。
根据3211111f f f f ++=总,其中f f f ==31,=2f ∞ 解得光具组的总焦距2f f =总 再由成像公式总f v u 111=+,得 f v 32= 总的放大率31==u v m ,像高为物高的13。
解法二:按陆续成像计算物AP 经LM 组合所成像的位置、大小。
物AP 经透镜L 成的像为第一像,取12u f =,由成像公式可得像距12v f =,即像在平向镜后距离2f 处,像的大小'H 与原物相同,'H H =。
第一像作为物经反射镜M 成的像为第二像。
第一像在反射镜M 后2f 处,对M 来说是虚物,成实像于M 前2f 处。
像的大小H ''也与原物相同,H H H '''==。
第二像作为物,而经透镜L 而成的像为第三像,这时因为光线由L 右方入射,且物(第二像)位于L 左方,故为虚物,取物32u f =-,由透镜公式33111u v f+=可得像距 333203fu v f u f ==>- 上述结果表明,第三像,即本题所求的像的位置在透镜左方距离23f 处,像的大小H '''可由3313v H H u '''==''求得,即 1133H H H '''''==,像高为物高的13。
例5、两个薄透镜L 1和L 2共轴放置,如图所示。
已知L 1的焦距f 1=f,L 2的焦距f 2=-f,两透镜间距离也是f 。
小物体位于物面P 上,物距u 1=3f 。
(1)小物体经这两个透镜所成的像在L 2的____边,到L 2的距离为____,是____像(虚或实)、____像(正或倒),放大率为____。
(2)现在把两透镜位置调换,若还要给定的原物体在原像处成像,两透镜作为整体应沿光轴向____边移动距离____。
这个新的像是____像(虚或实)、____像(正或倒),放大率为____。
分析与求解:(1)由题意知:f u 31=,f 1=f11111v u f += 得f v 5.11= 而ff f v d u 5.05.112-=-=-=22111v u f +=-,得f v =2 放大率15.035.121=⨯==ff f f m m m 所以像成在L 2的右边,到L 2的距离为f,像的放大率为1,是倒立的实像。
