理论力学课后答案-谢传峰、王琪-动力学第九章、第十章
理论力学答案解析[谢传峰版]
![理论力学答案解析[谢传峰版]](https://img.taocdn.com/s3/m/dc43c06e33687e21af45a930.png)
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学答案(谢传峰版)
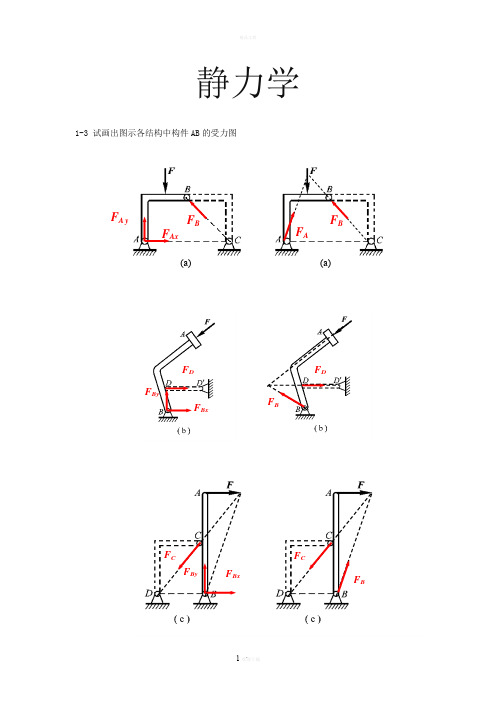
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yFB(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF Dy T E F CxF C yN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
45030对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学第七版答案解析第九章

9-10 在瓦特行星传动机构中,平衡杆O 1A 绕O 1轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装置在O 轴上,如图所示。
在O 轴上装有齿轮Ⅰ,齿轮Ⅱ与连杆AB 固连于一体。
已知:r 1=r 2=0.33m ,O 1A =0.75m ,AB =1.5m ;又平衡杆的角速度O 1=6rad/s 。
求当=60°且=90°时,曲柄OB 和齿轮Ⅰ的角速度。
题9-10图【知识要点】 Ⅰ、Ⅱ两轮运动相关性。
【解题分析】 本题已知平衡杆的角速度,利用两轮边缘切向线速度相等,找出ωAB ,ωOB 之间的关系,从而得到Ⅰ轮运动的相关参数。
【解答】 A 、B 、M 三点的速度分析如图所示,点C 为AB 杆的瞬心,故有 ABA O CA v A AB ⋅⋅==21ωω ωω⋅=⋅=A O CD v AB B 123所以 s rad r r v BOB /75.321=+=ωs rad r v CM v MAB M /6,1==⋅=I ωω 9-12 图示小型精压机的传动机构,OA =O 1B =r =0.1m ,EB =BD =AD =l =0.4m 。
在图示瞬时,OA ⊥AD ,O 1B ⊥ED ,O 1D 在水平位置,OD 和EF 在铅直位置。
已知曲柄OA 的转速n =120r/min ,求此时压头F 的速度。
题9-12图【知识要点】 速度投影定理。
【解题分析】 由速度投影定理找到A 、D 两点速度的关系。
再由D 、E 、F 三者关系,求F 速度。
【解答】 速度分析如图,杆ED 与AD 均为平面运动,点P 为杆ED 的速度瞬心,故 v F = v E = v D由速度投影定理,有A D v v =⋅θcos可得 s ll r n r v v A F /30.1602cos 22m =+⋅⋅==πθ 9-16 曲柄OA 以恒定的角速度=2rad/s 绕轴O 转动,并借助连杆AB 驱动半径为r 的轮子在半径为R 的圆弧槽中作无滑动的滚动。
理论力学答案(谢传峰版)精编版
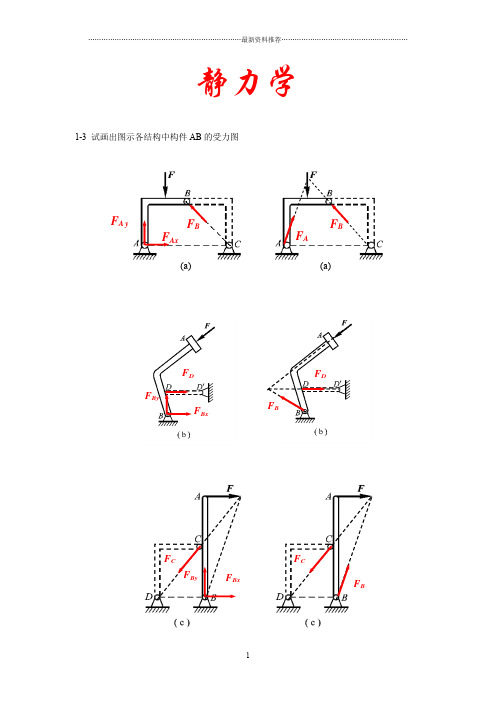
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学谢传锋第九章习题解答
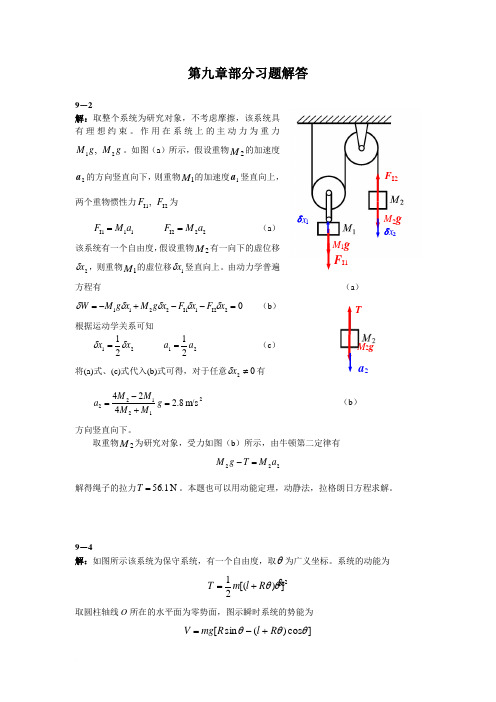
第九章部分习题解答9-2解:取整个系统为研究对象,不考虑摩擦,该系统具有理想约束。
作用在系统上的主动力为重力g M g M 21,。
如图(a )所示,假设重物2M 的加速度2a 的方向竖直向下,则重物1M 的加速度1a 竖直向上,两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =(a )该系统有一个自由度,假设重物2M 有一向下的虚位移2x δ,则重物1M 的虚位移1x δ竖直向上。
由动力学普遍方程有 (a )02I21I12211=--+-=x F x F x g M x g M W δδδδδ (b )根据运动学关系可知2121x x δδ=2121a a =(c )将(a)式、(c)式代入(b)式可得,对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a (b )方向竖直向下。
取重物2M 为研究对象,受力如图(b )所示,由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。
本题也可以用动能定理,动静法,拉格朗日方程求解。
9-4解:如图所示该系统为保守系统,有一个自由度,取θ为广义坐标。
系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面,图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2gF I2F I1δx 2δx 1M 2gT a 2拉格朗日函数V T L -=,代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。
9-6解:如图所示,该系统为保守系统,有一个自由度,取弧坐标s 为广义坐标。
系统的动能为221S m T =取轨线最低点O 所在的水平面为零势面,图示瞬时系统的势能为mgh V =由题可知b s ds dh 4sin ==ϕ,因此有b s d b s h So8s 42==⎰。
理论力学答案(谢传峰版)

静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF DxF Dy WT E F CxF C yWN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭45030的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学课后习题答案

理论力学课后习题答案理论力学课后习题答案引言:理论力学是物理学的基础课程之一,对于理解和应用物理学的原理和方法具有重要意义。
在学习理论力学的过程中,课后习题是巩固知识、提高能力的重要途径。
本文将针对理论力学课后习题进行解答,帮助读者更好地理解和掌握这门课程。
第一章:牛顿力学1. 一个物体以初速度v0沿直线运动,加速度为a,求物体的位移与时间的关系。
答:根据牛顿第二定律F=ma,可得物体所受合力F=ma=mv/t,其中m为物体的质量,v为物体的速度,t为时间。
由此可得物体的位移s=vt+1/2at^2。
2. 一个质点在重力作用下自由下落,求它在t时刻的速度和位移。
答:在重力作用下,质点的加速度为g,即a=g。
根据牛顿第二定律F=ma,可得质点所受合力F=mg。
根据牛顿第一定律,质点的速度随时间的变化率为v=g*t,位移随时间的变化率为s=1/2gt^2。
第二章:拉格朗日力学1. 一个质点沿半径为R的圆周运动,求它的动能和势能。
答:质点的动能由动能定理可得,即K=1/2mv^2,其中m为质点的质量,v为质点的速度。
质点的势能由引力势能可得,即U=-GmM/R,其中G为引力常数,M为圆周的质量。
2. 一个质点在势能为U(r)的力场中运动,求它的运动方程。
答:根据拉格朗日方程可得,质点的运动方程为d/dt(dL/dv)-dL/dr=0,其中L=T-U,T为质点的动能,U为质点的势能。
第三章:哈密顿力学1. 一个质点在势能为U(x)的力场中运动,求它的哈密顿量和哈密顿运动方程。
答:质点的哈密顿量由哈密顿定理可得,即H=T+U,其中T为质点的动能,U为质点的势能。
质点的哈密顿运动方程为dp/dt=-dH/dx,其中p为质点的动量。
2. 一个质点在势能为U(x)的力场中运动,求它的哈密顿正则方程。
答:质点的哈密顿正则方程为dx/dt=dH/dp,dp/dt=-dH/dx,其中x为质点的位置,p为质点的动量。
结论:通过对理论力学课后习题的解答,我们可以更深入地理解和应用物理学的原理和方法。
理论力学(谢传峰)_部分习题答案

/静力学部分1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bFAxF A y F DF ByF A F Bx F B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A y F B yF CxF Dy F Bx T EN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C 60o F 130o F BCx y45030F B杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
1 2
[
J
1
2
J 2 (
cos )2
J 3 (
sin )2 ]
4
取圆环最低点 A 所在的水平面为零势面,系统的势能为: V mgl cos
则拉格朗日函数:
动力学第五章部分习题解答
5-2 滑轮组上悬挂有质量为 10kg 的重物 M1 和质量为 8kg 的重物 M 2 ,如图所示。忽略滑轮
的质量,试求重物 M 2 的加速度 a2 及绳的拉力。
解: 取整个系统为研究对象,不考虑摩擦,该系统具有理 想约束。作用在系统上的主动力为重物的重力
M1g, M 2 g 。假设重物 M 2 的加速度 a2的方向竖直向
下,则重物 M1的加速度 a1竖直向上,两个重物惯性力
FI1, FI 2为:
FI2
FI1 M 1a1
FI 2 M 2 a2
(1)
该系统有一个自由度,假设重物 M 2 有一向下的虚位移
x2 ,则重物 M1的虚位移x1竖直向上。由动力学普遍
方程有:
δx1
M1g FI1
W M1gx1 M 2 gx2 FI1x1 FI 2x2 0
以角速度
绕铅垂边转动。忽略摩擦,试建立杆的相对运动微分方程。
解:
框架(质量不计)以匀角速度
绕铅垂边转动,该系统是保守系统,有一个自由度,取 AB 杆与铅垂边的夹角 为广义坐标。若以框架为动系,AB 杆上任意一点的速度是该点相对于
框架的相对速度和随框架运动的牵连速度的矢量和,且相对速度和牵连速度相互垂直。杆 AB 的动能可表示为相对于框架运动的动能和随框架转动的动能之和。AB 杆相对于框架作
于广义坐标 的广义力 QM 0 ;
取 0, 0 ,在这组虚位移下力偶 M 所作的虚功为[W ] M ,因此力偶 M
对应于广义坐标 的广义力 QM
[W ]
M;
代入拉格朗日方程
d dt
(
L
)
L
QM
0 ,整理可得:
解:
取楔块 ABC 和圆柱构成的系统为研
究对象,该系统为保守系统,有二个
自由度,取楔块水平滑动的位移 x , 零势面
vA
以及圆柱的转角(A 点 =0)为广
φ
义坐标。若以楔块为动系,楔块的速
度 vA ,圆柱轴心 O 的速度 vo ,以及
x
轴心 O 相对于 A 的相对速度满足如
vOr
下的矢量关系(方向如图所示):
绕 OC 轴的定轴转动,物体的绝对角速度 φ 是 和
的矢量之和。为了方便起见, 以 O1O2 为 x 轴, O3G 为 y 轴,如图建立一个固连在物体上的坐标系,将角速度是 和
在该坐标系上投影有: φ i
cos j
sin z 。
x’
z’ y’
2
2
取圆环最低点 A 所在的水平面为零势面,系统的势能 为:
V mgr(1 cos )
则拉格朗日函数:
L T V 1 mr2 (2
2 sin2 ) mgr(1 co 2
零势面
代入拉格朗日方程:
d dt
( L )
L Biblioteka 0,整理得质点的运动微分方程为:
绕铅垂直径 AB 转动,如 图所示。试建立质点的运动微分方程,并求维持圆环匀角速度转动所必需的转矩 M 。
2
解:
1.求质点的运动微分方程
圆环(质量不计)以匀角速度
绕铅垂轴 AB 转动,该 系统有一个自由度,取角度 为广义坐标。系统的动能
为:
T 1 m(r)2 1 m(
r sin )2
( g
2 cos )sin 0 r
2.求维持圆环作匀速转动的力偶 M 如果求力偶 M ,必须考虑圆环绕铅垂轴 AB 的一般转动。因此解除“圆环绕铅垂轴 AB 匀 速
转动”这一约束,将力偶 M 视为主动力。此时系统有两个自由度,去角度 和圆环绕轴 AB 的转角 为广义坐标,系统的势能不变,动能表达式中以 代替
1 g
P2
cosxs
1 2g
P2 s2
取过 x 轴的水平为零势面,系统的势能为:
V P2s sin
则拉格朗日函数:
L
T
V
1 2g
(P1
P2 )x 2
1 g
P2
cosxs
1 2g
P2 s2
P2s sin
将水平力 F 视为非有势力,它对应于广义坐标 x 和 s 的广义力计算如下: 取 x 0,s 0 ,在这组虚位移下力 F 所作的虚功为[W ]x Fx ,因此力 F 对应于广
则拉格朗日函数: L T V 1 mS 2 mg S 2
2
8b
代入拉格朗日方程:
d dt
(SL )
L S
0
,整理得摆的运动微分方程为:
S
g 4b
S
0,
解得质点的运动规律为: S Asin(1 2
g b
t
0
)
0
,其中
A,
0
微积分常数。
5-13 质量为 m 的质点沿半径为 r 的圆环运动,圆环以匀角速度
g
,方向水平向右。
楔块 B 的相对加速度: aBr
s
FP1 cos (P1 P2 )P2 sin P2 (P1 P2 sin2 )
g ,方向沿斜面向上。
5-18 在光滑水平面上放一质量为 m 的三角形楔块 ABC,质量为 m1 ,半径为 r 的均质圆柱沿
楔块的 AB 边滚动而不滑动,如图所示。试求楔块的加速度及圆柱的角加速度。
(1)
6
代入拉格朗日方程
d dt
(
L s
)
L s
QsF
F cos ,整理可得:
P2 cosx P2s (F cos P2 sin)g (2)
由方程(1)和方程(2)解得:
楔块 A 的加速度:
aA
x
F sin P2 cos P1 P2 sin2
该系统为保守系统,有一个自由度,取 为广义坐标。系统的动能为:
T 1 m[(l R )]2 2
1
取圆柱轴线 O 所在的水平面为零势面,系统 的势能为:
V mg[l R sin (l R ) cos ]
零势面
拉格朗日函数 L T V ,代入拉格朗日方
程有:
义坐标 x 的广义力 QxF F ; 取x 0,s 0 ,在这组虚位移下力 F 所作的虚功为[W ]s F coss ,因此力 F 对应
于广义坐标 s 的广义力 QsF F cos ;
代入拉格朗日方程
d dt
(
L x
)
L x
QxF
F ,整理可得:
(P1 P2 )x P2 coss Fg
点的运动规律。 解:
该系统为保守系统有一个自由度,取弧坐标 S
为广义坐标。系统的动能为:
T 1 mS 2 2
取轨线最低点 O 所在的水平面为零势面,系 统的势能为:
h 零势面
V mgh
由 题 可 知 dh sin S , 因 此 有 :
dS
4b
S
h
S dS S 2
0 4b
8b
平力 F ,如图所示。忽略摩擦,角 已知,试求楔块 A 的加速度及楔块 B 的相对加速度。
解:
取楔块 A,B 构成的系统为研究对象,该系统有
二个自由度,取楔块 A 水平滑动的位移 x ,以
s
及楔块 B 相对于 A 的沿斜面滑动的位移 s 为广
义坐标。若以楔块 A 为动系,楔块 A 的速度 vA ,
vO vA vOr
