全等三角形之手拉手模型专题
专题 全等三角形模型——手拉手模型与半角模型(解析版)

全等三角形模型——手拉手模型与半角模型手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点,如图所示结论:(1)△ABD ≌△AEC(2)∠α+∠BOC=180°(3)OA 平分∠BOC变形:1.如图,以ABC D 的边AB ,AC 为边,向外作等边ABD D 和等边ACE D ,连接BE ,CD 相交于点F .(1)求证:DC BE =.(2)求DFE Ð的度数.(3)求证:FA 平分DFE Ð.(4)求证:DF AF BF =+.【分析】(1)根据等边三角形的性质和全等三角形的判定和性质得出DC BE =即可;(2)根据全等三角形的性质和角的关系得出120DFE Ð=°即可;(3)过点A 作AP DC ^于P ,AQ BE ^于Q ,根据三角形面积公式和角平分线的性质解答即可;(4)在DF 上截取DM BF =,连接AM ,根据全等三角形的判定和性质解答即可.【解答】证明:(1)ABD D Q 和ACE D 是等边三角形,AD AB \=,AE AC =,60DAB EAC AEC ACE Ð=Ð=Ð=Ð=°,DAB BAC EAC BAC \Ð+Ð=Ð+Ð,即DAC BAE Ð=Ð,在DAC D 与BAE D 中,AD AB DAC BAE AC AE =ìïÐ=Ðíï=î,()DAC BAE SAS \D @D ,DC BE \=;(2)DAC BAE D @D Q ,ADF ABF \Ð=Ð,AGD FGB Ð=ÐQ ,60BFG DAG \Ð=Ð=°,120DFE \Ð=°;(3)过点A 作AP DC ^于P ,AQ BE ^于Q ,DAC BAE D @D Q ,\1122DAC BAE S DC AP S BE AQ D D =×==×,DC BE =Q ,AP AQ \=,AP DC ^Q ,AQ BE ^,FA \平分DFE Ð;(4)在DF 上截取DM BF =,连接AM ,在ADM D 与ABF D 中,AD AB ADM ABF DM BF =ìïÐ=Ðíï=î,()ADM ABF SAS \D @D ,AM AF \=,DAM BAF Ð=Ð,60DAB Ð=°Q ,60DAM MAG \Ð+Ð=°,60BAF MAG \Ð+Ð=°,即60MAF Ð=°,AMF \D 是等边三角形,MF AF \=,DF DM MF AF BF \=+=+.2.等边ABD D 和等边BCE D 如图所示,连接AE 与CD ,证明:(1)AE DC =;(2)AE 与DC 的夹角为60°;(3)AE 延长线与DC 的交点设为H ,求证:BH 平分AHC Ð.【分析】(1)根据ABD D 和BCE D 都是等边三角形,即可得到()ABE DBC SAS D @D ,进而得出AE DC =;(2)根据全等三角形的性质以及三角形内角和定理,即可得到ADH D 中,60AHD Ð=°,进而得到AE 与DC 的夹角为60°;(3)过B 作BF DC ^于F ,BG AH ^于G ,根据全等三角形的面积相等,即可得到BG BF =,再根据BF DC ^于F ,BG AH ^于G ,可得BH 平分AHC Ð.【解答】证明:(1)ABD D Q 和BCE D 都是等边三角形,AB DB \=,EB CB =,ABD EBC Ð=Ð,ABE DBC \Ð=Ð,在ABE D 和DBC D 中,AB DB ABE DBC EB CB =ìïÐ=Ðíï=î,()ABE DBC SAS \D @D ,AE DC \=;(2)ABE DBC D @D Q ,BAE BDC \Ð=Ð,又120BAE HAD ADB Ð+Ð+Ð=°Q ,120BDC HAD ADB \Ð+Ð+Ð=°,ADH \D 中,18012060AHD Ð=°-°=°,即AE 与DC 的夹角为60°;(3)如图,过B 作BF DC ^于F ,BG AH ^于G ,ABE DBC D @D Q ,ABE DBC S S D D \=,即1122AE BG DC BF ´=´,又AE DC =Q ,BG BF \=,又BF DC ^Q 于F ,BG AH ^于G ,BH \平分AHC Ð.3.(2021春•宁阳县期末)如图两个等腰直角ADC D 与EDG D ,90ADC EDG Ð=Ð=°,连接AG ,CE 交于点H .证明:(1)AG CE =;(2)AG CE ^.【分析】(1)由两个等腰直角ADC D 与EDG D ,可得AD CD =,DG DE =,90ADC GDE Ð=Ð=°,进而得出ADG CDE Ð=Ð,然后由SAS 即可判定ADG CDE D @D ,进而可得结论;(2)根据全等三角形的性质则可证得DAG DCE Ð=Ð,再根据直角三角形的两锐角互余进而证出90CHA Ð=°即可得解.【解答】解:(1)证明:ADC D Q 与EDG D 是等腰直角三角形,AD CD \=,DG DE =,且90ADC GDE Ð=Ð=°,ADC CDG GDE CDG \Ð+Ð=Ð+Ð,即ADG CDE Ð=Ð,在ADG D 与CDE D 中,AD CD ADG CDEDG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,AG CE \=;(2)证明:设CD 与AG 相交于点P ,由(1)知,ADG CDE D @D,DAG DCE \Ð=Ð,90ADC Ð=°Q ,90DAG APD \Ð+Ð=°,APD CPH Ð=ÐQ ,90DCE CPH \Ð+Ð=°,90CHP \Ð=°,AG CE \^.4.如图,两个等腰Rt ADC D 与Rt EDG D ,连接AG ,CE 交于点H ,连接HD .求证:AHD EHD Ð=Ð.【分析】由“SAS ”可证ADG CDE D @D ,可得AG CE =,ADG CDE S S D D =,由面积公式可得DN DM =,由角平分线的判定定理可得结论.【解答】证明:如图,过点D 作DN AG ^于N ,DM CE ^于M ,90ADC GDE Ð=Ð=°Q ,ADG EDC \Ð=Ð,在ADG D 和CDE D 中,AD CD ADG CDE DG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,AG CE \=,ADG CDE S S D D =,\1122AG DN CE DM ´´=´´,DN DM \=,又DN AG ^Q ,DM CE ^,AHD EHD \Ð=Ð.5.如图,两个正方形ABCD 和DEFG ,连接AG 与CE ,二者相交于H .问:(1)求证:ADG CDE D @D .(2)AG 与CE 的关系?并说明理由.(3)求证:HD 平分AHE Ð.【分析】(1)由四边形ABCD 与DEFG 是正方形,可得AD CD =,90ADC GDE Ð=Ð=°,进而得出ADG CDE Ð=Ð,DG DE =,然后由SAS 即可判定ADG CDE D @D ;(2)根据全等三角形的性质则可证得AG CE =,DAG DCE Ð=Ð,进而证出90CHA Ð=°即可;(3)根据全等三角形的性质和三角形的面积解答即可.【解答】(1)证明:Q 四边形ABCD 和四边形DEFG 是正方形,AD CD \=,DG DE =,且90ADC GDE Ð=Ð=°,ADG CDE \Ð=Ð,在ADG D 与CDE D 中,AD CD ADG CDE DG DE =ìïÐ=Ðíï=î,()ADG CDE SAS \D @D ,(2)解:AG CE =,AG CE ^,理由如下:由(1)得:ADG CDE D @D ,AG CE \=,DAG DCE Ð=Ð,DCE CHA DAG ADC Ð+Ð=Ð+ÐQ ,90CHA ADC \Ð=Ð=°,AG CE \^;(3)证明:过点D 作DM AG ^于M ,DN CE ^于N ,如图:ADG CDE D @D Q ,DCE ADG S S D D \=,\1122CE DN AG DM ´´=´´,DM DN \=,MD AG ^Q ,DN CE ^,DH \平分AHE Ð.6.(2021秋•南岗区校级期中)已知:AB AC =,AD AE =,BAC DAE Ð=Ð.(1)如图1,求证:BD CE =;(2)如图2,当60BAC Ð=°时,BD 、CE 交于点P ,连接PA ,求证:PB PC PA -=;(3)如图3,在(2)的条件下,过E 作EH PA ^于H ,在PE 上取点F ,连接FH 并延长至G ,使GH FH =,连接GE ,若2HGE HEG Ð=Ð,求EHF Ð的度数.【分析】(1)证明BAD CAE D @D 即可;(2)作AF BD ^,AG CE ^,截取PH PA =,证明ABF ACG D @D ,可推出60APF APG Ð=Ð=°,从而可证ACH ABP D @D ,进而得证;(3)作HQ CE ^于Q ,作HM GH =交GE 于M ,作MN AE ^于N ,证明HQF ENM D @D ,可推出15AEG Ð=°,进而求得结果.【解答】(1)证明:如图1,BAC DAE Ð=ÐQ ,BAC CAD DAE CAD \Ð+Ð=Ð+Ð,BAD CAE \Ð=Ð,AB AC =Q ,AD AE =,()BAD CAE SAS \D @D ,BD CE \=;(2)证明:如图2,设AC 与PB 交于I ,作AF BD ^于F ,AG CE ^于G ,在PE 上截取PH PA =,90AFB AGC \Ð=Ð=°,由(1)知:BAD CAE D @D ,B C \Ð=Ð,PIC AIB Ð=ÐQ ,60CPF BAC \Ð=Ð=°,AB AC =Q ,()AFB AGC AAS \D @D ,AF AG \=,11(180)(18060)6022APF APG CPF \Ð=Ð=°-Ð=°-°=°,PAH \D 是等边三角形,60AHC \Ð=°,AHC APB \Ð=Ð,()ABP ACH AAS \D @D ,PB CH PC PH PC PA \==+=+,即:PB PC PA -=;(3)解:如图3,作HQ CE ^于Q ,作HM GH =交GE 于M ,作MN AE ^于N ,90HQF MNE \Ð=Ð=°,AMG G Ð=Ð,2G AEG Ð=ÐQ ,2AMG AEG \Ð=Ð,AMG AEG EHM Ð=Ð+ÐQ ,AEG EHM \Ð=Ð,MH ME \=,12EN AN EH \==,GH FH =Q ,ME FH \=,PH HE ^Q ,90PHE \Ð=°,由(2)知:60APF Ð=°,30HEP \Ð=°,12HQ EH \=,HQ NE \=,()HQF ENM HL \D @D ,AEG QHF \Ð=Ð,EHF G AEG Ð=Ð+ÐQ ,3FHE AEG \Ð=Ð,4QHE QHF FHE AEG \Ð=Ð+Ð=Ð,90HQE \Ð=°,30HEP Ð=°,60HQE \Ð=°,460AEG \Ð=°,15AEG \Ð=°,345EHF AEG \Ð=Ð=°.7.(2021秋•天河区期末)ABC D 是等边三角形,点D 是AC 边上动点,(030)CBD ααÐ=°<<°,把ABDD 沿BD 对折,得到△A BD ¢.(1)如图1,若15α=°,则CBA Т= .(2)如图2,点P 在BD 延长线上,且DAP DBC αÐ=Ð=.①试探究AP ,BP ,CP 之间是否存在一定数量关系,猜想并说明理由.②若10BP =,CP m =,求CA ¢的长.(用含m 的式子表示)【分析】(1)由ABC D 是等边三角形知,60ABC Ð=°,由15CBD αÐ==°,知A BD ABD ABC α¢Ð=Ð=Ð-,2602CBA A BD ABC ααα¢¢Ð=Ð-=Ð-=°-,代入α值即可;(2)①连接CP ,在BP 上取一点P ¢,使BP AP ¢=,根据SAS 证△BP C APC ¢@D ,得CP CP ¢=,再证CPP ¢D 是等边三角形,即可得出BP AP CP =+;②先证180BCP BCA ¢Ð+Ð=°,即A ¢、C 、P 三点在同一直线上,得出PA PC CA ¢¢=+,根据SAS 证ADP D @△A DP ¢,得出A P AP ¢=,即可求出CA ¢的值.【解答】解:(1)ABC D Q 是等边三角形,60ABC \Ð=°,CBD αÐ=Q ,A BD ABD ABC α¢\Ð=Ð=Ð-,2602CBA A BD ABC ααα¢¢\Ð=Ð-=Ð-=°-,15α=°Q ,6021530CBA ¢\Ð=°-´°=°,故答案为:30°;(2)①BP AP CP =+,理由如下:连接CP ,在BP 上取一点P ¢,使BP AP ¢=,ABC D Q 是等边三角形,60ACB \Ð=°,BC AC =,DAP DBC αÐ=Ð=Q ,\△()BP C APC SAS ¢@D ,CP CP ¢\=,BCP ACP ¢Ð=Ð,60PCP ACP ACP BCP ACP ACB ¢¢¢¢\Ð=Ð+=Ð+Ð=Ð=°,CP CP ¢=Q ,CPP ¢\D 是等边三角形,60CPB \Ð=°,PP CP ¢=,BP BP PP AP CP ¢¢\=+=+,即BP AP CP =+;②如下图,由①知,60BPC Ð=°,180********BCP BPC PBC αα\Ð=°-Ð-Ð=°-°-=°-,由(1)知,602CBA α¢Ð=°-,由折叠知,BA BA ¢=,BA BC =Q ,BA BC ¢\=,11(180)[180(602)]6022BCA CBA αα¢¢\Ð=°-Ð=°-°-=°+,12060180BCP BCA αα¢\Ð+Ð=°-+°+=°,\点A ¢、C 、P 在同一直线上,即PA PC CA ¢¢=+,由折叠知,BA BA ¢=,ADB A DB ¢Ð=Ð,180180ADB A DB ¢\°-Ð=°-Ð,ADP A DP ¢\Ð=Ð,DP DP =Q ,ADP \D @△()A DP SAS ¢,A P AP ¢\=,由①知,BP AP CP =+,10BP =Q ,CP m =,10AP BP CP m \=-=-,10A P AP m ¢\==-,10102CA A P CP m m m ¢¢\=-=--=-.半角模型图形中,往往出现90°套45°的情况,或者120°套60°的情况。
专题04 手拉手模型证全等(解析版)

专题04 手拉手模型证全等类型一等边手拉手1.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)线段AN与线段BM交于点O,求∠AOM的度数;(3)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.【答案】(1)AN=BM,见解析;(2)60°;(3)等边三角形,见解析【解析】【分析】(1)证△ACN≌△MCB(SAS),即可得出AN=BM;(2)由全等三角形的性质得∠ANC=∠MBC,则∠AOM=∠CAN+∠MBC=∠CAN+∠ANC =∠BCN=60°;(3)证△ACE≌△MCF(ASA),得CE=CF,即可得出结论.【详解】解:(1)AN=BM,理由如下:∵△ACM、△CBN都是等边三角形,∴AC=CM,CN=CB,∠ACM=∠BCN=60°,∴∠ACM +∠MCN =∠BCN +∠MCN ,∴∠ACN =∠BCM ,在△ACN 和△MCB 中,AC MC ACN MCB CN CB =⎧⎪∠=∠⎨⎪=⎩,∴△ACN ≌△MCB (SAS ),∴AN =BM ;(2)由(1)得:△ACN ≌△MCB ,∴∠ANC =∠MBC ,∴∠AOM =∠CAN +∠MBC =∠CAN +∠ANC =∠BCN =60°;(3)△CEF 是等边三角形,理由如下:∵△ACN ≌△MCB ,∴∠CAE =∠CMF ,∵∠MCF =180°﹣∠ACM ﹣∠BCN =60°,∴∠ACE =∠MCF ,在△ACE 和△MCF 中,CAE CMF AC MCACE MCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACE ≌△MCF (ASA ),∴CE =CF ,∵∠MCF =60°,∴△CEF 是等边三角形.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.2.如图,△ABD 和△BCE 都是等边三角形,∠ABC <105°,AE 与DC 交于点F . (1)求证:AE =DC ;(2)求∠BFE 的度数;(3)若AF =9.17cm ,BF =1.53cm ,CF =7.53cm ,求CD .【答案】(1)见解析;(2)60°;(3)18.23cm【解析】【分析】(1)由等边三角形的性质可知∠DBA=∠EBC=60°,BD=AB,BC=BE.从而可证∠DBC =∠ABE.即可利用“SAS”可证明△DBC≌△ABE,得出结论AE=DC.(2)过点B作BN⊥CD于N,BH⊥AE于H.由△DBC≌△ABE可知∠BEH=∠BCN,∠BDF =∠BAF.再结合等边三角形的性质可求出∠FDA+∠DAF=120°,进而求出∠DF A=180°-120°=60°,即求出∠DFE=180°-60°=120°.即可利用“AAS”证明△BEH≌△BCN,得出结论BH=BN,即得出BF平分∠DFE,即可求出∠BFE=60°.(3)延长BF至Q,使FQ=AF,连接AQ.根据所作辅助线可知∠AFQ=∠BFE=60°,即证明△AFQ是等边三角形,得出结论AF=AQ=BQ,∠F AQ=60°.又可证明∠DAF=∠BAQ.利用“SAS”可证明△DAF≌△BAQ,即得出DF=BQ=BF+FQ=BF+AF,最后即可求出CD=DF+CF=BF+AF+CF=1.53+9.17+7.53=18.23cm.【详解】(1)证明:∵△ABD和△BCE都是等边三角形,∴∠DBA=∠EBC=60°,BD=AB,BC=BE,∴∠DBA+∠ABC=∠EBC+∠ABC,即∠DBC=∠ABE,∵在△DBC和△ABE中,BD ABDBC ABE BC BE=⎧⎪∠=∠⎨⎪=⎩,∴△DBC≌△ABE(SAS),∴AE=DC;(2)解:如图,过点B作BN⊥CD于N,BH⊥AE于H.∵△DBC ≌△ABE ,∴∠BEH =∠BCN ,∠BDF =∠BAF ,∵△ABD 是等边三角形,∴∠BDA +∠BAD =120°,∴∠FDA +∠DAF =120°,∴∠DF A =180°-120°=60°,∴∠DFE =180°-60°=120°,在△BEH 和△BCN 中,90BEH BCN BHE BNC BE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△BEH ≌△BCN (AAS ),∴BH =BN ,∴BF 平分∠DFE ,∴∠BFE =12∠DFE =12×120°=60°;(3)解:如图,延长BF 至Q ,使FQ =AF ,连接AQ .则∠AFQ =∠BFE =60°,∴△AFQ 是等边三角形,∴AF =AQ =BQ ,∠F AQ =60°,∵△ABD 是等边三角形,∴AD =AB ,∠DAB =60°,∴∠DAB +∠BAF =∠BAF +∠F AQ ,即∠DAF =∠BAQ ,在△DAF 和△BAQ 中,AD AB DAF BAQ AF AQ =⎧⎪∠=∠⎨⎪=⎩,∴△DAF ≌△BAQ (SAS ),∴DF =BQ =BF +FQ =BF +AF ,∴CD =DF +CF =BF +AF +CF =1.53+9.17+7.53=18.23cm .【点睛】本题为三角形综合题.考查等边三角形的判定和性质,全等三角形的判定和性质,三角形内角和定理以及角平分线的判定和性质.正确的作出辅助线也是解答本题的关键. 3.如图,点C 为线段BD 上一点,,ABC CDE △△都是等边三角形,AD 与CE 交于点,F BE 与AC 相交于点G .(1)求证:≌ACD BCE ;(2)求证:ACF BCG ≌(3)若8,25CF CG BD +==,求ACD △的面积.【答案】(1)见解析;(2)见解析;(3)【解析】【分析】(1)根据SAS 即可证明△BCE ≌△ACD ;(2)由△ACD ≌△BCE 可得∠CBG =∠CAF ,从而利用ASA 可证明△ACF ≌△BCG ;(3)求出CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,求出GM ,FN ,根据S △ACD =S △ACF +S △CDF =S △BCG +S △CDF 可求出答案.【详解】解:(1)证明:∵△ABC ,△CDE 是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠ACE =∠DCE +∠ACE ,即∠BCE =∠DCA ,∴△ACD ≌△BCE (SAS ).(2)由(1)得△ACD ≌△BCE ,∴∠CBG =∠CAF ,又∵∠ACF =∠BCG =60°,BC =AC ,在△ACF 和△BCG 中,ACF BCG BC ACCAF CBG ∠=∠⎧⎪=⎨⎪∠=⎩, ∴△ACF ≌△BCG (ASA );(3)∵△ACF ≌△BCG ,∴S △ACF =S △BCG ,CG =CF ,而CF +CG =8,∴CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,又∵∠ACB =∠DCE =60°,∴GM=FN= ∴S △ACD =S △ACF +S △CDF=S △BCG +S △CDF =12BC •GM +12CD •FN=12⨯(BC +CD )=【点睛】本题考查了全等三角形的判定和性质以及等边三角形的判定和性质,利用全等三角形的性质得出CG =CF 是解答此题的关键.类型二 等直手拉手4.已知:两个等腰直角三角板△ACB 和△DCE (AC =BC ,DC =CE ,∠ACB =∠DCE =90°)如图所示摆放,连接AE 、BD 交于点O .AE 与DC 交于点M ,BD 与AC 交于点N .(1)如图1(两个等腰直角三角板大小不等),试判断AE 与BD 有何关系并说明理由; (2)如图2(两个等腰直角三角板大小相等,即AC =DC ),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.【答案】(1)AE =BD 且AE ⊥BD .理由见解析;(2)△ACB ≌△DCE ,△EMC ≌△BCN ,△AON ≌△DOM ,△AOB ≌△DOE【解析】【分析】(1)证明△ACE ≌△BCD ,可得AE =BD ,∠CEA =∠BDC ,由∠CME =∠DMO ,根据三角形内角和定理即可得∠DOM =∠ECM =90°,进而可证AE ⊥BD .(2)根据三角形全等的判定找出相等边和角,进而找出全等三角形.【详解】解:(1)结论;AE =BD 且AE ⊥BD .理由如下:∵∠ACB =∠DCE ,∴∠ACB +∠DCA =∠DCE +∠DCA ,即∠DCB =∠ACE ,∵AC =BC ,CD =CE ,在△ACE 与△BCD 中,AC BC ACE DCB CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD (SAS ),∴AE =BD ,∠CEA =∠BDC ,∵∠CME =∠DMO ,∴180()180()CEA CME DMO BDC ︒-∠+∠=︒-∠+∠,即∠DOM =∠ECM =90°,∴AE ⊥BD ,∴AE =BD 且AE ⊥BD ;(2)∵AC =DC ,∴AC =CD =EC =CB ,在△ACB 与△DCE 中,AC DC ACB DCE CB CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACB ≌△DCE (SAS );由(1)可知:∠AEC =∠BDC ,∠EAC =∠DBC ,∴∠DOM =90°,∵∠AEC =∠CAE =∠CBD ,∴△EMC ≌△BCN (ASA ),∴CM =CN ,∴DM =AN ,∴△AON ≌△DOM (AAS ),∵DE =AB ,AO =DO ,∴△AOB ≌△DOE (HL ).【点睛】本题考查了三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键. 5.已知Rt ABC △中,AB AC =,90BAC ∠=︒,点D 为直线BC 上的一动点(点D 不与点B 、C 重合),以AD 为边作Rt ADE △,AD AE =,连接CE .(1)发现问题:如图①,当点D 在边BC 上时,①请写出BD 和CE 之间的数量关系________,位置关系________;②线段CE 、CD 、BC 之间的关系是_________;(2)尝试探究:如图②,当点D 在边BC 的延长线上且其他条件不变时,(1)中CE 、CD 、BC 之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;(3)拓展延伸:如图③,当点D 在边CB 的延长线上且其他条件不变时,若6BC =,1CE =,则线段AD 的长为________.【答案】(1)①BD CE =,BD CE ⊥.②BC CE CD =+.(2)不成立,CE BC CD =+.(3)5【解析】【分析】(1)①根据全等三角形的判定定理证明△BAD ≌△CAE ,根据全等三角形的性质证明; ②根据全等三角形的对应边相等证明即可;(2)证明△BAD ≌△CAE ,根据全等三角形的性质解答即可;(3)根据△BAD ≌△CAE 得到BD =CE =1,再证明△DCE 是直角三角形,利用勾股定理求出DE ,即可求出AD 的长度;【详解】(1)①解:结论:BD =CE ,BD ⊥CE ,理由:∵∠ABC =∠ACB =45°,∠ADE =∠AED =45°,∴∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∠ACE =∠B =45°,∴∠BCE =90°,即BD ⊥CE ,故答案为:BD =CE ;BD ⊥CE ;②证明:∵BD =CE ,∴BC =BD +CD =CE +CD ;故答案为:BC CE CD =+.(2)解:(1)中BC 、CE 、CD 之间存在的数量关系不成立,新的数量关系是CE =BC +CD , 理由:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∴CE =BC +CD ;(3)解:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE =1,∠ABD =∠ACE =135°,∵∠ACB =45°,∴∠DCE =90°,在Rt △DCE 中,CD =BD +BC =7,CE =1,∴DE=∴52AD ==; 故答案为:5.【点睛】本题考查三角形综合题,等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.6.在△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点.(1)如图1,E 、F 分别是AB 、AC 上的点,且BE =AF 、求证:△DEF 是等腰直角三角形经过分析已知条件AB =AC ,D 为BC 的中点.容易联想等腰三角形三线合一的性质,因此,连结AD (如图2),以下是某同学由己知条件开始,逐步按层次推出结论的流程图.请帮助该同学补充完整流程图.补全流程图:①___≅____,②∠EDF =___(2)如果E 、F 分别为AB 、CA 延长线上的点,仍有BE =AF ,其他条件不变,试猜想△DEF是否仍为等腰直角三角形?请在备用图中补全图形、先作出判断,然后给予证明.【答案】(1)△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由见解析【解析】【分析】(1)连接AD ,根据∠BAC =90°,AB =AC ,D 为BC 的中点,可以得到∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===,从而可以证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,由∠ADE +∠BDE =∠BDA =90°,可得∠ADE +∠ADF =90°,即∠EDF =90°,即可证明;(2)连接AD ,同样证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,再由∠ADF +∠BDF =∠BDA =90°,即可得到∠BDE +∠BDF =90°,即∠EDF =90°,即可证明.【详解】解:(1)如图所示,连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠B =∠BAD =∠CAD ,在△BDE 和△ADF 中,BD AD B DAF BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴DE =DF ,∠BDE =∠ADF ,∵∠ADE +∠BDE =∠BDA =90°,∴∠ADE +∠ADF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形;故答案为:△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由如下:连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠ABC =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠F AD =180°-∠CAD =135°,∠EBD =180°-∠ABC =135°,∴∠F AD =∠EBD ,在△BDE 和△ADF 中,BD AD EBD FAD BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴∴DE =DF ,∠BDE =∠ADF ,∵∠ADF +∠BDF =∠BDA =90°,∴∠BDE +∠BDF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形.【点睛】本题主要考查了全等三角形的性质与判定,等腰直角三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.7.(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE 之间的数量关系__________;(2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)【答案】(1)90°,AD =BE ;(2)AD =BE ,AD ⊥BE ;(3)α【解析】【分析】(1)由已知条件可得AC BC =,CD CE =,进而根据∠ACB −∠DCB =∠DCE −∠DCB ,可得∠ACD =∠BCE ,证明△ACD ≌△BCE (SAS ),即可求得AD =BE ;∠BEC =∠CDA =135°;(2)延长AD 交BE 于点F ,同理可得△ACD ≌△BCE ,设∠F AB =α,则∠CAD =∠CBE =45°-α,根据∠ABE =45°+45°-α=90°-α,进而根据∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°,即可求解;(3)延长BE 交AD 于点G ,方法同(2)证明△ACD ≌△BCE ,进而根据三角形的内角和定理即可求得直线AD 和BE 的夹角.【详解】(1)∵ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,∴AC BC =,CD CE =,∠CDE =45°∴∠CDA =135°∵∠ACB −∠DCB =∠DCE −∠DCB ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠BEC =∠ADC =135°,AD =BE∴∠AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ⊥BE ,理由如下,同理可得△ACD ≌△BCE ,则AD =BE ,延长AD 交BE 于点F ,设∠F AB =α,则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE(3)如图,延长BE 交AD 于点G ,∵ACB △和DCE 均为等腰三角形,∴AC BC =,CD CE =,∵∠ACB =∠DCE =α,∵∠ACB +∠ACE =∠DCE +∠ACE ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD∵ACB DCE α∠=∠=∴∠CBA =∠CAB =()11180=9022αα︒-︒- ∴∠GAB +∠GBA =()()CAD CAB ABC CBE ∠+∠+∠-∠,ABC CAB =∠+∠180α=︒-,∴∠AGB =180°-(∠GAB +∠GBA )α= ,即直线AD 和BE 的夹角为α.故答案为:α.【点睛】本题考查了等腰三角形的性质,三角形内角和定理,全等三角形的性质与判定,掌握旋转模型证明三角形全等是解题的关键.8.已知:等腰Rt ABC 和等腰Rt ADE △中,AB AC =,AE AD =,90BAC EAD ∠=∠=︒.(1)如图1,延长DE 交BC 于点F ,若68BAE ∠=︒,则DFC ∠的度数为;(2)如图2,连接EC 、BD ,延长EA 交BD 于点M ,若90AEC ∠=︒,求证:点M 为BD 中点;(3)如图3,连接EC 、BD ,点G 是CE 的中点,连接AG ,交BD 于点H ,9AG =,5HG =,直接写出AEC △的面积.【答案】(1)68︒;(2)见解析;(3)36【解析】【分析】(1)由已知条件可得45D C ∠=∠=︒,对顶角AQD CQF ∠=∠,则DAC DFC ∠=∠,根据DAE CAB ∠=∠即可的DFC BAE ∠=∠;(2)过点B 作ME 的垂线交EM 的延长线于N ,证明AEC BNA △≌△,得AE BN =,进而可得AD NB =,再证明DAM BNM △≌△即可得证点M 为BD 中点;(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,先证明ABE ACD △≌△,进而证明AEG KCG △≌△,根据角度的计算以及三角形内角和定理求得BAD KCA ∠=∠,进而证明ABD CAK △≌△,再根据,90CAG ABD BAC ∠=∠∠=︒,证明AH BD ⊥,根据已知条件求得ABD S最后证明AEC ABD S S =即可.【详解】 (1)设DF 交AC 于Q ,如图1,ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △AQD CQF ∠=∠180,180DAQ D AQD QFC C CQF ∠=-∠-∠∠=-∠-∠DAQ QFC ∴∠=∠90BAC EAD ∠=∠=︒即BAE EAQ EAQ QAD ∠+∠=∠+∠BAE QAD ∴∠=∠DFC BAE ∴∠=∠68BAE ∠=︒68DFC ∴∠=︒故答案为68︒(2)如图2,过点B 作ME 的垂线交EM 的延长线于N ,90N ∴∠=︒90AEC =︒∠N AEC ∴∠=∠90BAC ∠=︒90EAC NAB ∴∠+∠=︒90NAC ACE ∠+∠=︒NAB ECA ∴∠=∠ ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AD AE ∴== 又AC AB =∴AEC BNA △≌△NB AE ∴=AE AD =AD NB ∴=90DAE ∠=︒DAM N ∴∠=∠又DMA BMN ∠=∠DAM BNM ∴△≌△DM BM ∴=即M 是BD 的中点(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,如图90BAC EAD ∠=∠=︒即BAE EAC EAC CAD ∠+∠=∠+∠BAE CAD ∴∠=∠ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AE AD ∴==在ABE △与ACD △中,AE AD BAE CAD AB AC =⎧⎪∠=∠⎨⎪=⎩∴ABE △≌ACD △(SAS )ABE ABD S S ∴=△△,BE CD = G 点是EC 的中点EG GC ∴=AGE KGC ∠=∠,AG GK =AGE KGC ∴△≌△(SAS )∴,AE CK AEG KCG =∠=∠,AE KC AD ∴==ACK ACB BCE KCG ∠=∠+∠+∠45AEC BCE =︒+∠+∠45ABC BAP =︒+∠+∠90BAE =︒+∠BAD =∠AKC ABD ∴△≌△(SAS )18BD AK ∴==,CAK ABD ∠=∠90BAG CAG ∠+∠=︒90ABD BAG ∴∠+∠=︒即90AHB ∠=︒9AG =,5HG =954AH AG HG ∴=-=-=111843622ABD S BD AH ∴=⋅=⨯⨯=△ 36AEC AEG AGC GCK AGC ACK ABD S S S S S S S =+=+===△△△△△△△∴AEC S 36=【点睛】本题考查了三角形全等的性质与判定,等腰直角三角形的性质,三角形内角和定理,三角形外角性质,构造辅助线是解题的关键.类型三 等腰手拉手9.已知:如图,在△ABC 中,AB =AC ,在△ADE 中,AD =AE ,且∠BAC =∠DAE ,连接BD ,CE 交于点F ,连接AF .(1)求证:△ABD ≌△ACE ;(2)求证:F A 平分∠BFE .【答案】(1)见解析(2)见解析【解析】【分析】(1)根据SAS 证明结论即可;(2)作AM ⊥BD 于M ,作AN ⊥CE 于N .由(1)可得BD =CE ,S △BAD =S △CAE ,然后根据角平分线的性质即可解决问题.(1)证明:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS );(2)证明:如图,作AM ⊥BD 于M ,作AN ⊥CE 于N .由△BAD ≌△CAE ,∴BD =CE ,S △BAD =S △CAE , ∵1122BD AM CE AN ⋅⋅=⋅⋅, ∴AM =AN ,∴点A 在∠BFE 平分线上,∴F A 平分∠BFE .【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.10.如图,在等腰△ABC 与等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE =α,连接BD 和CE 相交于点P ,交AC 于点M ,交AD 于点N .(1)求证:BD=CE.(2)求证:AP平分∠BPE.(3)若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.【答案】(1)见解析(2)见解析(3)PE=AP+PD,见解析【解析】【分析】(1)由“SAS”可证△BAD≌△CAE,可得BD=CE;(2)由全等三角形的性质可得S△BAD=S△CAE,由三角形面积公式可得AH=AF,由角平分线的性质可得AP平分∠BPE;(3)由全等三角形的性质可得∠BDA=∠CEA,由“SAS”可证△AOE≌△APD,可得AO=AP,可证△APO是等边三角形,可得AP=PO,可得PE=AP+PD,即可求解.(1)证明:∵∠BAC=∠DAE=α,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)证明:如图,过点A作AH⊥BD,AF⊥CE,∵△BAD≌△CAE,∴S△BAD=S△CAE,BD=CE,∴12BD×AH=12CE×AF,∴AH=AF,又∵AH⊥BD,AF⊥CE,∴AP平分∠BPE;(3)解:PE=AP+PD,理由如下:如图,在线段PE上截取OE=PD,连接AO,∵△BAD≌△CAE,∴∠BDA=∠CEA,又∵OE=PD,AE=AD,∴△AOE≌△APD(SAS),∴AP=AO,∵∠BDA=∠CEA,∠PND=∠ANE,∴∠NPD=∠DAE=α=60°,∴∠BPE=180°-∠NPD=180°-60°=120°,又∵AP平分∠BPE,∴∠APO=60°,又∵AP=AO,∴△APO是等边三角形,∴AP =PO ,∵PE =PO +OE ,∴PE =AP +PD .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的判定和性质以及角之间的关系,证明△BAD ≌△CAE 是解本题的关键.11.如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,连接BD ,CE ,BD 与CE 交于点O ,BD 与AC 交于点F .(1)求证:BD =CE .(2)若∠BAC =48°,求∠COD 的度数.(3)若G 为CE 上一点,GE =OD ,AG =OC ,且AG ∥BD ,求证:BD ⊥AC .【答案】(1)见解析;(2)132°;(3)见解析【解析】【分析】(1)根据∠BAC =∠DAE ,推出∠BAD =∠CAE ,从而结合“SAS ”证明△BAD ≌△CAE ,即可得出结论;(2)根据外角定理推出∠COD =∠OBC +∠BCA +∠ACE ,结合全等三角形的性质推出∠COD =∠ABC +∠BCA ,最后在△ABC 中利用内角和定理求解即可;(3)连接AO ,根据题意确定△ADO ≌△AEG ,得到∠OAD =∠GAE ,AO =AG ,再结合题干条件推出△AOC 为等腰三角形,以及∠BOA =∠BOC ,从而根据“三线合一”证明即可.【详解】(1)证:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即:∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE (SAS ),∴BD =CE ;(2)解:∵∠COD =∠OBC +∠BCO ,∠BCO =∠BCA +∠ACE ,∴∠COD =∠OBC +∠BCA +∠ACE ,∵△BAD ≌△CAE ,∴∠ABD =∠ACE ,∴∠COD =∠OBC +∠BCA +∠ABD =∠ABC +∠BCA ,∵∠BAC =48°,∴∠ABC +∠BCA =180°-48°=132°,∴∠COD =132°;(3)证:如图所示,连接AO ,∵△BAD ≌△CAE ,∴∠ADO =∠AEG ,在△ADO 和△AEG 中,E A ADO A G E E D G D A O =⎧⎪⎨⎪∠==⎩∠ ∴△ADO ≌△AEG (SAS ),∴∠OAD =∠GAE ,AO =AG ,∴∠AOG =∠AGO ,∴∠OAD +∠DAG =∠GAE +∠DAG ,即:∠OAG =∠DAE ,∵∠DAE =∠BAC ,∴∠BAC =∠OAG ,在△ABF 和△COF 中,∠BAC =180°-∠ABD -∠AFB ,∠BOC =180°-∠ACE -∠CFO , 由(2)知∠ABD =∠ACE ,∵∠AFB =∠CFO ,∴∠BAC =∠BOC ,∴∠BOC =∠OAG ,∵AG ∥BD ,∴∠BOA =∠OAG ,∴∠BOA =∠BOC ,∵AO =AG ,AG =CO ,∴AO =CO ,即:△AOC为等腰三角形,∵∠BOA=∠BOC,∴OF⊥AC,∴BD⊥AC.【点睛】本题考查全等三角形的判定与性质,等腰三角形的判定与性质等,掌握全等三角形的判定与性质,熟悉“手拉手”模型的证明是解题关键.类型四手拉手综合12.现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA 所在直线上.以MN为边作如图所示的等边△MNP.(1)如图1,当M在线段OA上时,证明:AM﹣AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.【答案】(1)见解析;(2)AM+AN=AP,理由见解析【解析】【分析】(1)在AB上取点C,使得AC=AM,则△ACM为等边三角形,结合“手拉手”模型证明△CMN≌△AMP,得到CN=AP,即可得证;(2)在射线AO上取点D,使得AN=AD,仿照(1)的过程证明△DNM≌△ANP,即可得到AP=DM,从而得出结论.【详解】证:(1)由题意可知,∠BAO =60°,如图所示,在AB 上取点C ,使得AC =AM ,则△ACM 为等边三角形,MC =MA ,∠CMA =60°,∵△NMP 为等边三角形,∴MN =MP ,∠NMP =60°,∴∠CMA =∠NMP ,∴∠CMA -∠NMA =∠NMP -∠NMA ,∴∠CMN =∠AMP ,在△CMN 和△AMP 中,M M CMN A P P A N M C M M =⎧⎪⎨⎪∠==⎩∠ ∴△CMN ≌△AMP (SAS ),∴CN =AP ,∴CN +AN =AP +AN =AC ,∵AC =AM ,∴AP +AN =AM ,∴AM -AN =AP ;(2)AM +AN =AP ,理由如下:如图所示,在射线AO 上取点D ,使得AN =AD ,∵∠BAO =60°,∴△AND 为等边三角形,ND =NA ,∠DNA =60°,∵△NMP 为等边三角形,∴NM =NP ,∠MNP =60°,∴∠DNA =∠MNP ,∴∠DNA +∠ANM =∠MNP +∠ANM ,∴∠DNM =∠ANP ,在△DNM 和△ANP 中,N N DNM A P P A M N D N N =⎧⎪⎨⎪∠==⎩∠ ∴△DNM ≌△ANP (SAS ),∴AP =DM ,∵AN =AD ,DA +AM =DM ,∴AN +AM =AP .【点睛】本题考查等边三角形的性质,全等三角形的判定与性质等,掌握双等边三角形中“手拉手”模型是解题关键.13.已知:△ABC 与△BDE 都是等腰三角形.BA =BC ,BD =BE (AB >BD )且有∠ABC =∠DBE .(1)如图1,如果A 、B 、D 在一直线上,且∠ABC =60°,求证:△BMN 是等边三角形; (2)在第(1)问的情况下,直线AE 和CD 的夹角是 °;(3)如图2,若A 、B 、D 不在一直线上,但∠ABC =60°的条件不变则直线AE 和CD 的夹角是 °;(4)如图3,若∠ACB =60°,直线AE 和CD 的夹角是 °.【答案】(1)证明见解析;(2)60;(3)60;(4)60;【解析】【分析】(1)根据题意,得∠ABC =∠DBE =60°,从而得ABE DBC ∠=∠;通过证明ABE CBD ≌,得BAE BCD ∠=∠;通过证明BAM BCN ≌,得BM BN =,根据等边三角形的性质分析,即可完成证明;(2)结合题意,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;结合(1)的结论,根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解;(3)同理,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;通过证明ABE CBD ≌,得BAE BCD ∠=∠;根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解; (4)根据题意,通过证明ABC 为等边三角形,推导得ABE CBD ∠=∠,通过证明ABE CBD ≌,得BAE BCD ∠=∠,结合三角形外角的性质计算,即可得到答案.【详解】(1)∵∠ABC =∠DBE =60°∴18060MBN ABC DBE ∠=︒-∠-∠=︒,ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠ ∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠ BAM 和BCN △中 60BAE BCD AB BC ABC MBN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴BAM BCN ≌∴BM BN =∴BMN △为等边三角形;(2)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒根据题意,AE 和CD 相交于点O∵BAE BCD ∠=∠∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(3)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒∵ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠,∠ABC =∠DBE =60°∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠如图,延长AE ,交CD 于点O∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(4)∵BA =BC ,∴ACB CAB ∠=∠∵∠ACB =60°∴60ACB CAB ∠=∠=︒∴ABC 为等边三角形∵BD =BE ,∠ABC =∠DBE∴60DBE ∠=︒∵ABE ABC CBE ∠=∠-∠,CBD DBE CBE ∠=∠-∠∴ABE CBD ∠=∠ABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠分别延长CD 、AE ,相较于点O ,如下图:∴AOF OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOF BAC BCA ∠=∠+∠=︒∴18060AOC AOF ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60.【点睛】本题考查了等腰三角形、等边三角形、全等三角形、补角、三角形外角的知识;解题的关键是熟练掌握等边三角形、全等三角形、三角形外角的性质,从而完成求解.14.在ABC 中,AB =AC ,点D 是直线BC 上一点(不与B ,C 重合),以AD 为一边在AD 的右侧作ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE .(1)(请直接写出你的结论)如图1,当点D 在线段BC 上:①如果∠BAC =90°,则∠BCE =°;②如果∠BAC =100°,则∠BCE =°;(2)设∠BAC =α,∠BCE =β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.【答案】(1)①90;②80;(2)①α+β=180°,理由见解析;②图见解析,α+β=180°或α=β【解析】【分析】、(1)①由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD≌△CAE,可得∠ABC=∠ACE=45°,可求∠BCE的度数;②由等腰三角形的性质求出∠ABD=∠ACB=40°,由“SAS”可证△ABD≌△ACE得出∠ABD =∠ACE=40°,则可得出结论;(2)①由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论;②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论.【详解】解:(1)①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;②∵∠BAC=100°,AB=AC,∴∠ABD=∠ACB=40°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=40°,∴∠BCE =∠ACE +∠ACB =40°+40°=80°,故答案为:80.(2)①α+β=180°,理由:∵∠BAC =∠DAE ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC .即∠BAD =∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B =∠ACE .∴∠B +∠ACB =∠ACE +∠ACB .∵∠ACE +∠ACB =β,∴∠B +∠ACB =β,∵α+∠B +∠ACB =180°,∴α+β=180°.②如图1:当点D 在射线BC 上时,α+β=180°,连接CE ,∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,在△ABC 中,∠BAC +∠B +∠ACB =180°,∴∠BAC +∠ACE +∠ACB =∠BAC +∠BCE =180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.【点睛】本题主要考查全等三角形的判定及性质,等腰三角形的性质和三角形内角和定理,掌握全等三角形的判定方法及性质是关键.15.小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;(2)拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由.【答案】(1)见解析;(2)60°,BE=AD;(3)∠AEB=90°,AE=BE+2CM,理由见解析【解析】【分析】(1)先判断出∠BAD=∠CAE,进而利用SAS判断出△BAD≌△CAE,即可得出结论;(2)同(1)的方法判断出△BAD≌△CAE,得出AD=BE,∠ADC=∠BEC,最后用角的差,即可得出结论;(3)同(2)的方法,即可得出结论.【详解】解:(1)∵△ABC和△ADE均是顶角为40°的等腰三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)∵△ABC和△ADE均是等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=∠CDE=∠CED=60°,∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵∠CDE=60°,∴∠BEC=∠ADC=180°﹣∠CDE=120°,∵∠CED=60°,∴∠AEB=∠BEC﹣∠CED=60°,故答案为:60°,BE=AD;(3)AE=BE+2CM,理由:同(1)(2)的方法得,△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵△CDE是等腰直角三角形,∴∠CDE=∠CED=45°,∴∠ADC=180°﹣∠CDE=45°,∴∠BEC=∠ADC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM=ME=CM.∴AE=AD+DE=BE+2CM.。
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
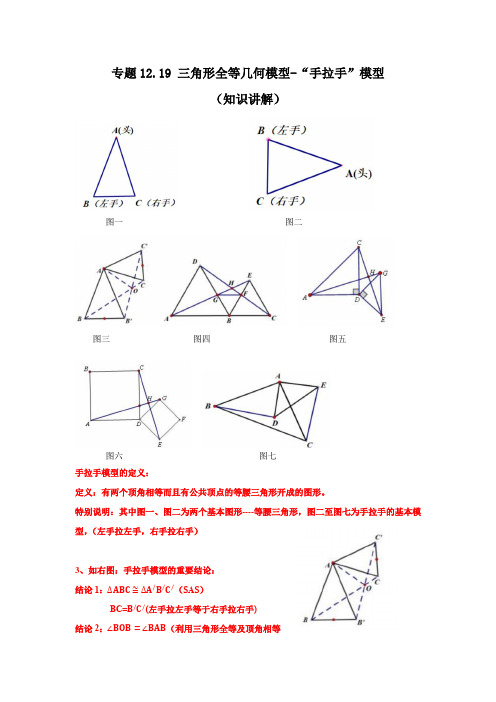
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
全等三角形之手拉手模型

全等三角形之手拉手模型专题
手拉手模型:
定义:所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型:
例题:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
共顶点的等腰直角三角形中的手拉手
变式精练1、下图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,求证:⑴ BD=CE ⑵ BD⊥CE
共顶点的等边三角形中的手拉手
变式精练2:如图,点A为线段BD上一点,△ABC和△ADE均是等边三角形,求:(1)CD=BE (2)∠DAE+∠BFD=180° (3)∠BFA=∠DFA=60°
模型应用1:如图,分别以△ABC 的边AB、AC 同时向外作等腰直角三角形,其中AB =AE ,AC =AD,∠BAE =∠CAD=90°,点G为BC中点,点F 为BE 中点,
点H 为CD中点。
探索GF 与GH 的位置及数量关系并说明理由。
(选讲)模型应用2:如图,在五边形ABCDE中,∠ABC =∠AED =90°,∠BAC =∠EAD=α,F 为CD的中点。
求证:(1)BF=EF
课堂小测:
练习1:如图,两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。
求:(1)AG=CE (2)AG与CE之间的夹角为多少度?(3)HD平分∠AHE。
专题12 全等三角形模型之手拉手模型全攻略(解析版)四川成都七年级数学下册-

专题12全等三角形模型之手拉手模型全攻略【模型说明】【例题精讲】例1(等边三角形)如图,已知B C E、、三点共线,分别以BC CE、为边作等边ABC∆和等边CDE∆,连接BD AE、分别与AC CD、交于,M N AE、与BD的交点为F.(1)求证:BD AE=;(2)求AFB∠的度数;(3)连接MN,求证://BCMN【答案】(1)证明见解析(2)60AFB∠=︒(3)证明见解析【分析】(1)根据等边三角形的性质去证明BCD ACE≌,即可得证BD AE=;(2)根据等边三角形的性质得60ABC BAC∠=∠=︒,再根据(1)中BCD ACE≌可得CAE DBE=∠∠,再根据三角形的外角的性质即可求出AFB∠的度数;(3)根据等边三角形的性质去证明BCM ACN△≌△,可得CM CN=,从而求得60CMN ACB==︒∠∠即可得证//MN BC.【详解】(1)∵ABC∆和CDE∆是等边三角形∴,,60AC BC CD CE ACB DCE====︒∠∠∴,BCD ACB ACD ACE DCE ACD=+=+∠∠∠∠∠∠∴BCD ACE∠=∠在△BCD和△ACE中AC BCBCD ACECE BD=⎧⎪∠=∠⎨⎪=⎩∴BCD ACE≌拓展研究:(2)如图③,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A 、D 、E 在同一条直线上,CF 为△DCE 中DE 边上的高,连接BE .请求∠AEB 的度数及线段CF 、AE 、BE 之间的数量关系,并说明理由.【答案】(1)证明见解析;∠AEB=60︒;(2)∠AEB=90︒;2AE BE CF =+;理由见解析.【分析】(1)小雪的题目:先利用SAS 证明ADC BEC ≅ ,再利用全等三角形的性质、三角形外角的性质及等量代换即可得证;小华的题目:先利用SAS 证明ADC BEC ≅ ,再利用全等三角形的性质得出ADC BEC ∠∠=,然后根据等边三角形的性质求出60CDE CED ∠=∠=︒,最后根据邻补角的概念和角的和与差即可得出答案;(2)根据题意易证ADC BEC ≅ ,再根据全等三角形的性质及邻补角的概念即可求得∠AEB 的度数;然后根据三线合一即可得出CF DF EF ==,最后根据线段的和与差及等量代换即可得出答案.【详解】(1)小雪的题目:证明:ACB DCE∠=∠ ACD BCE∠∠∴=在ADC △和DCE △中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△CAD CBE∴∠=∠又ACD BCE ∠=∠ ,CDE CAD ACD∠=∠+∠CDE CBE BCE ∴∠=∠+∠;小华的题目:解:ACB DCE∠=∠ ACD BCE∠∠∴=在ADC △和DCE △中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△ADC BEC∠∠∴=CDE 为等边三角形60CDE CED ∴∠=∠=︒又 点A 、D 、E 在同一条直线上120ADC BEC ∴∠=∠=︒60AEB BEC CED ∴∠=∠-∠=︒(2)∠AEB=90︒;2AE BE CF =+;理由如下:△ACB 和△DCE 均为等腰直角三角形,,,9045AC BC CD CE ACB DCE CDE CED ∴==∠=∠=︒∠=∠=︒,,ACB DCB DCE DCB∴∠-∠=∠-∠即ACD BCE∠=∠在ADC △和DCE △中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△,BE AD BEC ADC ∴=∠=∠,点A 、D 、E 在同一直线上18045135ADC ∴∠=︒-︒=︒135BEC ∴∠=︒1354590AEB BEC CED ∴∠=∠-∠=︒-︒=︒90,DCE CD CE CF DE∠=︒=⊥ ,CF DF EF∴==2DE DF EF CF∴=+=2AE AD DE BE CF ∴=+=+.【点睛】本题考查了全等三角形的判定及性质、等腰三角形的性质、等边三角形的性质,熟练掌握性质定理是解题的关键.例4.(拓展)如图,在ABC 中,90C ∠=︒,AC BC =,点O 是AB 中点,90MON ∠=︒,将MON ∠绕点O 旋转,MON ∠的两边分别与射线AC 、CB 交于点D 、E .(1)当MON ∠转动至如图一所示的位置时,连接CO ,求证:COD BOE ≅ ;(2)当MON ∠转动至如图二所示的位置时,线段CD 、CE 、AC 之间有怎样的数量关系?请说明理由.【答案】(1)见解析(2)CE ﹣CD =AC .理由见解析【分析】(1)结论:CD CE AC +=.连接OC .证明()ASA COD BOE ≅ ;(2)结论:CE CD AC -=,证明方法类似(1).【详解】(1)证明:∵AC BC =,90C ∠=︒,AO OB =,∴OC AB ⊥,OC AO OB ==,∴45OCD B ∠=∠=︒,∵90MON COB ∠=∠=︒,∴DOC EOB ∠=∠,在COD △和BOE △中,OCD B OC OB OCD BOE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA COD BOE ≅ .(2)解:CE CD AC -=.理由:连接OC .∵AC BC =,90C ∠=︒,AO OB =,∴OC AB ⊥,OC AO OB ==,∴45OCD B ∠=∠=︒,∴135DOC CBE ∠=∠=︒,∵90MON COB ∠=∠=︒,∴DOC EOB ∠=∠,在COD △和BOE △中,OCD B OC OB OCD BOE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA COD BOE ≅ ,∴CD BE =,∴CE CD CE BE BC AC -=-==.【点睛】本题考查等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.例5.(培优综合)已知,在ABC ∆中,90BAC ︒∠=,45ABC ︒∠=,点D 为直线BC 上一动点(点D 不与点B C ,重合),以AD 为边作正方形ADEF ,连接CF .(1)如图①,当点D 在线段BC 上时,求证CF CD BC +=.(2)如图②,当点D 在线段BC 的延长线上时,其他条件不变,请直接写出CF BC CD ,,三条线段之间的关系.(3)如图③,当点D 在线段BC 的反向延长线上,且点A ,F 分别在直线BC 的两侧时,其他条件不变,请直接写出CF BC CD ,,三条线段之间的关系.【答案】(1)见解析;(2)CF CD BC -=,见解析;(3)CD CF BC -=,见解析.【分析】(1)△ABC 是等腰直角三角形,利用SAS 即可证明△BAD ≌△CAF ,从而证得CF=BD ,据此即可证得;(2)同(1)相同,利用SAS 即可证得△BAD ≌△CAF ,从而证得BD=CF ,即可得到CF-CD=BC ;(3)同理,证明△BAD ≌△CAF 即可得出结论.【详解】(1)证明:如图1,∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC ,∵四边形ADEF 是正方形,∴AD=AF ,∠DAF=90°,∵∠BAD=90°-∠DAC ,∠CAF=90°-∠DAC ,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩===,∴△BAD ≌△CAF (SAS ),∴BD=CF ,∵BD+CD=BC ,∴CF+CD=BC ;(2)解:CF-CD=BC .理由如下:如图2,∵∠BAD=90°+∠CAD ,∠CAF=90°+∠CAD ,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩===,∴△BAD ≌△CAF (SAS ),∴BD=CF ,∵BD=BC+CD ,∴CF-CD=BC .【答案】65°【分析】先判断出ACD BCE∆,再判断出≅∆(1)①如图1,求证:ABD ACE ≌△△;②当点D 在BC 边上时,请直接写出ABC ,ACD 所满足的关系;(2)当点D 在BC 的延长线上时,试探究ABC ,ACD ,ACE △的面积(ABC S ,ACD S ,ACE S )所满足的关系,并说明理由.【答案】(1)①证明见解析;②AC ABC C D A E S S S =+ ,理由见解析(2)ACE ABC ACD S S S =+△△△,理由见解析【分析】(1)①先证明BAD CAE ∠=∠,再利用SAS 证ABD ACE ≌△△即可;②利用全等三角形的性质得到ABD ACE S S = ,再由ABC ACD ABD S S S =+△△△即可得到结论;(2)由已知条件可得证出,ABD ACE ≌△△,推出ABD ACE S S = ,再由ABD ABC ACD S S S =+△△△,即可得到ACE ABC ACD S S S =+△△△.【详解】(1)证明:①∵BAC DAE ∠=∠,∴BAC CAD DAE CAD ∠-∠=∠-∠,即BAD CAE ∠=∠.在ABD △和ACE △中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩。
人教版八年级上册第十二章全等三角形专题手拉手模型讲义(无答案)
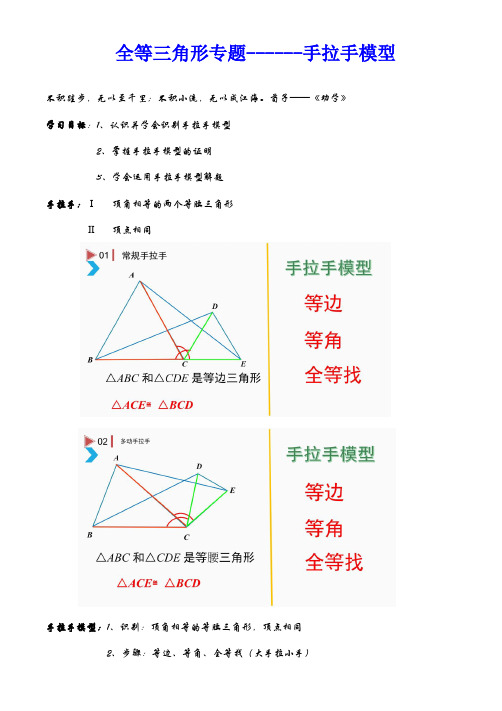
全等三角形专题------手拉手模型不积跬步,无以至千里;不积小流,无以成江海。
荀子——《劝学》学习目标:1、认识并学会识别手拉手模型2、掌握手拉手模型的证明3、学会运用手拉手模型解题手拉手:Ⅰ顶角相等的两个等腰三角形Ⅱ顶点相同手拉手模型:1、识别:顶角相等的等腰三角形,顶点相同常见图形【例1】如图在直线ABC的同一侧作两个等边三角形ABD∆,连结AE与CD,∆与BCE证明以下常用结论:1、DBC∆ABE∆≅2、DCAE=3、AE与DC之间的夹角为︒60(底边夹角等于顶角)4、DFB∆AGB∆≅5、CFB≅∆EGB∆6、连接GF,则B GF∆为等边三角形7、BH平分AHC∠8、ACGF//9、AH=DH+BH,CH=EH+BH(截长补短法)【变式精练1】如图两个等边三角形ABD∆,连结AE与CD,∆与BCE证明(1)DBC∆ABE∆≅(2)DCAE=60(3)AE与DC之间的夹角为︒(4)AE与DC的交点设为H,BH平分AHC∠【变式精练2】如图两个等边三角形ABD∆,连结AE与CD,∆与BCE证明(1)DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)AE与DC的交点设为H,BH平分AHC∠【例2】如图,两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H 问:(1)CDE∆是否成立?≅ADG∆(2)AG是否与CE相等?(3)AG与CE之间的夹角为多少度?(4)HD是否平分AHE∠?【例3】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立?(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?【例4】两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立?(2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度?(4)HB 是否平分AHC ∠?综合练习1、如图,C 为线段AE 上一动点(不与点A 、E 重合),在AE 同侧分别作正∆ABC 和正∆CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ ,以下五个结论: ①AD=BE ②PQ∥AE ③AP=BQ④DE=DP ⑤∠AOB=60°恒成立的结论有 __________________ (填序号)分别是线段 BE 和AD 的中点,则△CPM 是()A.钝角三角形B.直角三角形C.等边三角形D.非等腰三角形3、如图,△DAC 和△EBC 均是等边三角形,AE、BD 分别与CD、CE 交于点 M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是()A.3 个B.2 个C.1 个D.0 个4、如图,四边形ABCD、BEFG 均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.5、、(1)问题发现如图 1,△ACB 和△DCE 均为等边三角形,点A,D,E 在同一直线上,连接BE.填空:①∠AEB 的度数为___________;②线段 AD,BE 之间的数量关系为_________ (2)拓展探究如图 2,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点 A,D,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接 BE,请判断∠AEB 的度数及线段CM, AE,BE 之间的数量关系,并说明理由.。
初二上学期全等三角形专题之手拉手模型教案(有答案)

手拉手模型互动精讲【知识梳理】定义: 两个顶角相等且有共顶点的等腰三角形形成的图形。
(左手拉左手,右手拉右手)常见的手拉手模型:【例题精讲】例1、如图,分别以△ABC的AB、AC为边向外作等边三角形△ABD、△ACE,连接CD、BE交于F,求证(1)△DAC≌△BAE (2)求∠DFB的度数(3)AF 平分∠DFE.例2、以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.(1)试判断BD、CE的数量关系,并说明理由;(2)延长BD交CE于点F,试求∠BFC的度数;(3)把两个等腰直角三角形按如图2放置,(1)中的结论是否仍成立?请说明理由.F G HDECBA【课堂练习】1、如图,直线AB 的同一侧作△ABD 和△BCE 都为等边三角形,连接AE 、CD ,二者交点为H 。
求证: (1)△ABE ≌△DBC ; (2)AE=DC ; (3)∠DHA=60°; (4)△AGB ≌△DFB ; (5)△EGB ≌△CFB ; (6)连接HB ,HB 平分∠AHC 。
(7)连接GF ,GF ∥AC ;2、已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F(1) 如图1,若∠ACD=60°,则∠AFD=__________(2) 如图2,若∠ACD=α,连接CF,则∠AFC=__________(用含α的式子表示)(3) 将图1中的△ACD绕点C顺时针旋转如图3,连接AE、AB、BD,∠ABD=80°,求∠EAB的度数课堂检测1、如图甲,正方形ABCD和正方形CEFG共一顶点C,且B,C,E在一条直线上.连接BG,DE.(1)请你猜测BG,DE的位置关系和数量关系,并说明理由;(2)若正方形CEFG绕C点顺时针方向旋转一个角度后,如图乙,BG和DE是否还有上述关系?是说明理由.2、已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE. (1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE 的大小关系;(2)如图②③,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.课后作业1、如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB.点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足|m-2n|2+|n-2|=0(1) 求点D的坐标(2) 求∠AKO的度数(3) 如图2,点P、Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON、MN、BM的数量关系并证明2、如图△AOB和△ACD是等边三角形,其中AB⊥x轴于E点.(1)如图,若OC=5,求BD的长度;(2)设BD交x轴于点F,求证:∠OFA=∠DFA;(3)如图,若正△AOB的边长为4,点C为x轴上一动点,以AC为边在直线AC下方作正△ACD,连接ED,求ED的最小值.。
全等三角形专题复习手拉手模型

---初识手拉手
一、知识准备
已知: ∵∠BAC=∠B’AC’(已知) ∴∠BAC-∠CAB’=∠B’AC’即∠BAB’=
(等式的性质)
二、互动探究
(一)由倒下的直角板想到
Байду номын сангаас
二、互动探究
(二)常见“手拉手”模型的构成及证明
1.共顶点的两个等腰直角三角形构成的手拉手模型
二、互动探究
思考:手拉手模型中的变与不变,及两个三角形 全等的证明
(1)不论三角形旋转到什么位置,哪两对线段始终是相 等的? (2)哪一对角在旋转过程中,大小在变化,但始终是相 等的?
二、互动探究
例1.已知,如图,在∆ABC和∆A’B’C’中, A’C=B’C,AC=BC,∠ACB=∠A’CB’=90〫. 求证:∆ACA’ ∆BCB’
三、小结反思
三个常见手拉手模型共同特征是:
四、直击期末
如图,∠BAD=∠CAE=90〫,AB=AD,AE=AC,AF⊥CB,垂足为F。 求证:(1)∆ABC ∆ADE (2)求∠FAE的度数 (3)延长CF到G点,使BF=GF,连接AG。求证:CD=CG;并 猜想CD与2BF+DE的关系
回顾上面的问题及证明过程,你了解到手拉手模型 有哪些特征?
二、互动探究
2.共顶点的两个等边三角形构成的手拉手模型 例2.如图,已知∆ABC和∆AED是等边三角形。 求证:BD=CE
二、互动探究
3.共顶点的两个正方形构成的手拉手模型
例3.如图,四边形ABCD和四边形DEFG都是 正方形。 求证:(1)∆EDC ≌ ∆GDA (2)AG⊥CE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形之手拉手模型专题
基本图形1、图(1)中,C点为线段AB上一点,△ ACM △ CBN是等边三角形,AN 与BM相等吗说明理由;
如图(2)C点为线段AB上一点,等边三角形ACM和等边三角形CBN在
AB的异侧,此时AN与BM相等吗说明理由;
如图(3)C点为线段AB外一点,△ ACM △ CBN是等边三角形,AN与BM 相等吗
说明理由.
分析:题中三问均是对等边三角形性质的考查以及全等三角形的证明,由已知条件,利用等边三角形的性质可找出对应边及夹角相等,证明全等,即可得到线段相等.
解:(1)相等.
证明如下:•••△ ACM △ CBN是等边三角形,
••• AC=CM CN=BC
又/ ACN=/ MCN+60 / MCB M MCN+60 ,
•••/ ACN=/ MCB
•△ ACNm MCB •- AN=BM
(2)相等.
证明如下:•••△ ACM △ CBN是等边三角形,
•AC=CM CN=BC 又/ ACN=/ MCB
•△ ACNm MCB
•AN=BM
(3)相等.
证明如下:•••△ ACM △ CBN是等边三角形,
•AC=CM CN=BC
又/ ACN=/ MCN+60 / MCB M MCN+60 ,
•/ ACN=/ MCB
•△ ACNm MCB
•AN=BM
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得三角形全等是正确解答本题的关键.
图(1) 图(3)
变形
2、( 1)如图1,点C是线段AB上一点,分别以AC, BC为边在AB的同侧作等边△ ACM 和厶CBN连接AN, BM分别取BM AN的中点E,F,连接CE CF,EF.观察并猜想△ CEF的形状,并说明理由.
(2)若将(1 )中的“以AC, AC BC为
腰在AB的同侧作等腰△ 那么(1)中的
结论还成立吗若成立,由.
得出AN=BM, / ANC=Z MBA ,再证
△ NFC^^ BEC得出CE=CF / BCE=/ NCF利用等边三
角形的角度60 , 得出/ ECF=60 ,证得结论成立;
(2)证明过程如上(1)中的结论只有CE=CF而/ ECF只等于等腰三角形的顶角工60°,得出结论不成立.
解:(1)如图1 , △ CEF是等边三角形,
理由:•••等边△人。
皿和厶CBN
••• AC=MC BC=NC / ACN=/ MCB
在厶ACN和厶MCB中
NC= BC
/ ACN=Z MCB
AC= MC
•△ ACNm MCB( SAS ,
•AN=MB / ANC=/ MBA
在厶NFC和厶BEC中,
NC= BC
/ FNC=Z EBC
NF= BE
•△ NFC^A BEC( SAS ,
•EC=CF
•••/ BCE+Z ECN=60 , / BCE2 NCF,
•/ ECF=60 ,
•△ CEF是等边三角形;
(2)如图2,不成立,首先/ ACN^Z MCB
•△ ACN与厶MCB不全等.
如果有两个等腰三角形的顶角相等,那么结论也不成立,
证明方法与上面类似,只能得到CE=CF而Z ECF只等于等腰三角形的顶角工60°
点评:此题综合考查等边三角形的性质与判定,三角形全等的判定与性
质,等腰三角形的性质等知识点.
BC为边作等边△ ACM和厶CBN改为“以
ACM和厶CBN”如图2,其他条件不变,加以证
明;若不成立,请说明理
变形3、如图,在△ ABC 中,已知/ DBC=60 , AO BC,,又△ ABC、△ BCA、△ CAB都是△ ABC形外的等边三角形,而点D在AC上, 且BC=DC
(1)证明:△ C BD^A B' DC
(2)证明:△ AC DB' A;
证明:(〔)△ C BD与厶ABC中,
BC=DC AB=BC,/ C BD=60 +/ ABD2 ABC
•••△ C BD^A ABC ••• C D=AC
又在△ BCA与厶DCB中,
BC=DC AC=B C,Z ACB=/ B' CD=60 , • △ BCA^A DCB .•••
DB' =BA
•••△ C' BD^A B' DC
(2 )由(1)的结论知:
C D=B' C=AB ,
B ' D=B
C =AC , 又••• AD=AD
• △ AC DB' A.。
