第五章能控性、能观性与传递函数
合集下载
控制系统的能控性和能观性课件
唯一的，因为我们关心的只是它能否将
驱动到
，而不计较
的轨迹如何。
2. 线性连续时变系统的能控性定义
线性连续时变系统:
3. 离散时间系统 这里只考虑单输入的n阶线性定常离散系统:
3
3.2 线性定常系统的能控性判别
线性定常系统能控性判别准则有两种形式，一种是先将系统进行状态变
换，把状态方程化为约旦标准型
3.1 能控性的定义 3.2 线性定常系统的能控性判别 3.3 线性连续定常系统的能观性 3.4 离散时间系统的能控性与能观性 3.5 时变系统的能控性与能观性 3.6 能控性与能观性的对偶关系 3.7 状态空间表达式的能控标准型与能观标准型 3.8 线性系统的结构分解 3.9 传递函数阵的实现问题 3.10 传递函数中零极点对消与状态能控性和能观
一地确定任意初始状态矢量
，则系统是完全能观的，现根据此定义推
导能观性条件。从式(1)，有:
(3)
若系统能观，那么在知道
时，应能确定
出
，
，现从式(7)可得：
写成矩阵形式:
16
(4) 有唯一解的充要条件是其系数矩阵的秩等于 。这个系数矩阵称为 能观性矩阵。仿连续时间系统，记为N。即
(5)
17
3.5 时变系统的能控性与能观性
3.5.1 能控性判别 1.有关线性时变系统能控性的几点说明 1)定义中的允许控制 ，在数学上要求其元在 绝对平方可积的，即
区间是
这个限制条件是为了保证系统状态方程的解存在且唯一。 2)定义中的 ，是系统在允许控制作用下，由初始状态 目标状态(原点)的时刻。
转移到
3)根据能控性定义, 可以导出能控状态和控制作用之问的关系式。 4)非奇异变换不改变系统的能控性。
线性控制系统的能控性与能观测性修改
6
几点说明：根据初始状态和终端状态的不同位置， 可以分为：
1、系统的状态能控性： （常用） 初始状态为状态空间任意非零有限点；终端状态 为状态空间原点，即零态。
如果存在一个分段连续的输入u(t)，能在[t0, t f ] 的有 限时间内使得系统的某一初始状态 x(t0) 转移到零 态 x(tf ) 0 ，则称系统是状态能控的。
x1 1 2 2 x1 2
Байду номын сангаас
x 2
0
1
1
x2
0
u
x3 1 0 1 x3 1
[解]：
2
1）构造能控性判别矩阵： B 0,
1
1 2 2 2 4
AB
0
1
1
0
1
1 0 1 1 1
1 2 2 4 0
A2B
0
1
1
1
0
1 0 1 1 5
x4
4 0
0 4
1
x1 1
x2
1
x3 0
0
4
x4
3
0 2 0 6
1
3 u 状态不完全能控
0 9
18
二、秩判据
对于线性连续定常系统：x Ax Bu 状态完全能控的 充分必要条件是其能控性判别矩阵：
M [B AB A2B An1B] 满秩
即： rankM rank[B AB A2B An1B] n
x1 7 0 0 x1 2
1）
x 2
0
5
0
x2
5
u
x3 0 0 1 x3 7
状态完全能控
x1 7 0 0 x1 2
2）
x 2
0
几点说明：根据初始状态和终端状态的不同位置， 可以分为：
1、系统的状态能控性： （常用） 初始状态为状态空间任意非零有限点；终端状态 为状态空间原点，即零态。
如果存在一个分段连续的输入u(t)，能在[t0, t f ] 的有 限时间内使得系统的某一初始状态 x(t0) 转移到零 态 x(tf ) 0 ，则称系统是状态能控的。
x1 1 2 2 x1 2
Байду номын сангаас
x 2
0
1
1
x2
0
u
x3 1 0 1 x3 1
[解]：
2
1）构造能控性判别矩阵： B 0,
1
1 2 2 2 4
AB
0
1
1
0
1
1 0 1 1 1
1 2 2 4 0
A2B
0
1
1
1
0
1 0 1 1 5
x4
4 0
0 4
1
x1 1
x2
1
x3 0
0
4
x4
3
0 2 0 6
1
3 u 状态不完全能控
0 9
18
二、秩判据
对于线性连续定常系统：x Ax Bu 状态完全能控的 充分必要条件是其能控性判别矩阵：
M [B AB A2B An1B] 满秩
即： rankM rank[B AB A2B An1B] n
x1 7 0 0 x1 2
1）
x 2
0
5
0
x2
5
u
x3 0 0 1 x3 7
状态完全能控
x1 7 0 0 x1 2
2）
x 2
0
能控性与能观性
c11 c12 c c22 21 y (t ) c m1 cm 2 c1n e1t x10 c2 n e2t x20 nt cmn e xn 0
假使输出矩阵C中有某一列全为零，譬如说第2列中c12, c22, …, cm2均为零，则在 t y(t)中将不包含 e 2 x20这个自由分量，亦即不包含 x2(t)这个状态变量，很明显，这 个x2(t)不可能从y(t)的测量值中推算出来，即x2(t)是不能观的状态。
系统是状态完全能控的
x 2 1 x2 b2u y c1 c2 x
1 1 b1 x x u; 0 0 1
对于式(3-5)的系统
x 1 1 x1 x2 b1u x 2 1 x2
x2不受u(t)的控制，而为不能控的系统。
对式(3-3)的系统，系统矩阵A为对角线型，其标量微分方程形式为
x 1 1 x1
x 2 2 x2 b2u
x 2
x 1
1 1 0 x x u; 0 1 b2
对于式(3-4)的系统
y c1 c2 x
x 1 1 x1 x2
c13 c23 c33
1 2 1t 1t 1t e x10 te x20 t e x30 2! x1 (t ) 1t 1t e x20 te x30 这时，状态方程的解为 x(t ) x2 (t ) x ( t ) 3 1t e x 30
从而
y1 (t ) c11 c12 y (t ) y2 (t ) c21 c22 y3 (t ) c31 c32
假使输出矩阵C中有某一列全为零，譬如说第2列中c12, c22, …, cm2均为零，则在 t y(t)中将不包含 e 2 x20这个自由分量，亦即不包含 x2(t)这个状态变量，很明显，这 个x2(t)不可能从y(t)的测量值中推算出来，即x2(t)是不能观的状态。
系统是状态完全能控的
x 2 1 x2 b2u y c1 c2 x
1 1 b1 x x u; 0 0 1
对于式(3-5)的系统
x 1 1 x1 x2 b1u x 2 1 x2
x2不受u(t)的控制，而为不能控的系统。
对式(3-3)的系统，系统矩阵A为对角线型，其标量微分方程形式为
x 1 1 x1
x 2 2 x2 b2u
x 2
x 1
1 1 0 x x u; 0 1 b2
对于式(3-4)的系统
y c1 c2 x
x 1 1 x1 x2
c13 c23 c33
1 2 1t 1t 1t e x10 te x20 t e x30 2! x1 (t ) 1t 1t e x20 te x30 这时，状态方程的解为 x(t ) x2 (t ) x ( t ) 3 1t e x 30
从而
y1 (t ) c11 c12 y (t ) y2 (t ) c21 c22 y3 (t ) c31 c32
3-3 能控性、能观性与传递函数
B PO B
CO
y [1 0
C CPO 1
线性变换后
0 xO 2 xO 2
0 0 x O 1 u 0 x O 1 1
xO 0 ] xO
即：
s n y ( s ) a n 1 s n 1 y ( s ) a1 sy ( s ) a0 y ( s ) β0 u ( s ) y ( n ) a n 1 y ( n 1) a1 y a0 y β0 u
进行拉普拉斯反变换 选择系统的状态变量
（51）
3.9
实现问题
在基于状态空间方法分析和设计控制系统时，要知道系统的状态空间表达式。然 而在有的情况下，只知道系统的传递函数（矩阵），这时就要将给定的传递函数 （矩阵）描述变成与之输入输出特性等价的状态空间表达式描述。这个问题称为 系统实现问题。这里只讨论SISO系统的实现问题。
如果给定一个传递函数 g (s ) ，求得一个系统方程
（37）
y β0
a1
β1
β n 1 x du
3.7
能控性、能观性与传递函数的关系
x Ax B u y Cx
1
考察SISO线性定常系统 （40）
其传递函数为
g ( s ) C [ sI A] b
C adj[ sI A] b det[ sI A]
x Ax B u y Cx
（52） （53）
或者
x Ax bu y Cx du
注：当传递函数分子的阶次小于分母的阶次时，有（52）式形式； 当传递函数分子的阶次等于分母的阶次时，有（53）式形式。
传函与能控和能观性之间的关系
能控性； 若在c(sI-A)-1和c(sI-A)-1b的计算均有零极点对消发生，即同时发生ห้องสมุดไป่ตู้输出
方程和状态方程中，则影响能观性和能控性； 若零极点对消发生在预解矩阵 (sI-A)-1中， A的最小多项式阶次小于其特
征多项式阶次，表明约当标准型中等特征值对应多个约当块，可以证明，系 统必是不能控、不能观的。
可见把单输入单输出系统两个串联子系统的位置次序互换，在传递函数发生零极点 相消时，其能控性与能观性的结论也将互换。
能控、能观性和传递函数的关系
同一个系统 的不同状态空间模型会带来能控性和能观性的差 异
利用零极点对消判断单-单系统的能控性、能观性
W (s) c(sI A)1 b
若零极点对消发生在 c(sI-A)-1 的计算中，即发生在输出方程中，则影响 能观性； 若零极点对消发生在 c(sI-A)-1b的计算中，即发生在状态方程中，则影响
W (s) c(sI A)1 b
的分子分母无零极点对消。 若W(s)出现零极点对消，辅以传递函数实现的具体结构， 可
以判断不能控或不能观的具体情况。
中的零极点对消
若传递函数存在零极点对消,则 传递函数的部分分式中缺少 相应项.
例4.33 分析α=γ时系统的能控性与能观性。
U(s)
s s
X2(s)
1 s
Y(s) X1(s)
为串联关系
W ( s)
s 1 s s
W (s) 1 s
若α=γ，出现零极点对消。
系统状态结构图为
u
s 1 s s
-
x
2
∫
x2
-
x
课件-现代控制理论-刘豹第三版-第5章
能控性与能观性的判别方法
能观性判别方法
能控性判别方法
表示系统是否可以通过输入控制实现任意状态转移。若系统完全能控，则可以通过设计合适的控制器实现任意状态轨迹的跟踪或镇定；若部分能控或不能控，则存在状态无法被有效控制的风险。
能控性的物理意义
表示系统状态是否可以通过输出完全反映出来。若系统完全能观，则可以通过观测输出信号来准确估计系统状态；若部分能观或不能观，则存在状态无法被准确观测的风险，进而影响控制性能的实现。
控制系统稳定性分析是控制理论的核心内容之一，对于确保控制系统的正常运行具有重要意义。
章节内容结构
稳定性概念及定义
介绍稳定性的基本概念和定义，包括Lyapunov稳定性和BIBO稳定性等。
线性系统稳定性判据
详细阐述线性系统稳定性的判据，如Routh-Hurwitz判据、Nyquist判据和Bode图等。
图解法
状态转移矩阵的计算方法
1
2
3
状态转移矩阵反映了系统在时间间隔内从初始状态到最终状态的动态变化过程。
描述系统状态的动态变化过程
若系统稳定，则状态转移矩阵将逐渐趋于零，表示系统状态将逐渐趋于稳定。
反映系统稳定性
状态转移矩阵是进行系统分析和设计的重要工具，可用于研究系统的稳定性、能控性、能观性等性质。
非线性系统稳定性分析
介绍非线性系统稳定性分析方法，如相平面法、Lyapunov直接法等。
熟练掌握线性系统稳定性的判据和分析方法，能够应用所学知识分析和设计线性控制系统。
了解非线性系统稳定性分析方法的基本原理和应用范围，能够运用所学知识分析和设计简单的非线性控制系统。
掌握稳定性的基本概念和定义，理解不同稳定性定义之间的联系与区别。
能控性和能观性
状态能控性判据（三）
如果输入u(t)对状态X(t)的传递函数（阵） 没有零极点对消，那么系统可控，否则系 统不可控。
( sI − A ) −1 B
状态能控性判据例子5
状态能控性判据 MATLAB 实现
MATLAB中可以用ctrb(A,B)函数求系统的能 控判别矩阵M，并用RANK（M）求M的秩。
A=[1 2 0;3 -1 1;0 2 0]; B=[2;1;1]; C=[0 0 1]; D=0; To1=obsv(A,C) [Ao1,Bo1,Co1,Do1]=ss2ss(A,B,C,D,To1)
Ex_2ObsvI.m
离散时间系统的可控性/可观性
（略，自学）
若系统（A,B）具有两两相异的特征值， 则系统状态完全能控的充要条件为：系统 经过线性变换成对角规范型后， + Bu ⎥ λn ⎥ ⎦
B 不包含元素全为0的行。
状态能控性判据例子3
⎡ x1 ⎤ ⎡ −7 0 0 ⎤ ⎡ x1 ⎤ ⎡ 2 ⎤ ⎢ x ⎥ = ⎢ 0 −5 0 ⎥ ⎢ x ⎥ + ⎢ 5 ⎥ u ⎢ 2⎥ ⎢ ⎥⎢ 2⎥ ⎢ ⎥ ⎢ x3 ⎥ ⎢ 0 0 −1⎥ ⎢ x3 ⎥ ⎢ 7 ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ ⎡ x1 ⎤ ⎡ −7 0 0 ⎤ ⎡ x1 ⎤ ⎡ 0 1 ⎤ ⎢ x ⎥ = ⎢ 0 −5 0 ⎥ ⎢ x ⎥ + ⎢ 4 0 ⎥ ⎡ u1 ⎤ ⎢ 2⎥ ⎢ ⎥⎢ 2⎥ ⎢ ⎥ ⎢u ⎥ ⎢ x3 ⎥ ⎢ 0 0 −1⎥ ⎢ x3 ⎥ ⎢ 7 5 ⎥ ⎣ 2 ⎦ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦ ⎡ x1 ⎤ ⎡ −7 0 0 ⎤ ⎡ x1 ⎤ ⎡ 2 ⎤ ⎢ x ⎥ = ⎢ 0 −5 0 ⎥ ⎢ x ⎥ + ⎢ 0 ⎥ u ⎢ 2⎥ ⎢ ⎥⎢ 2⎥ ⎢ ⎥ ⎢ x3 ⎥ ⎢ 0 0 −1⎥ ⎢ x3 ⎥ ⎢ 9 ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ ⎣ ⎦
(整理)控制系统的能控性和能观测性
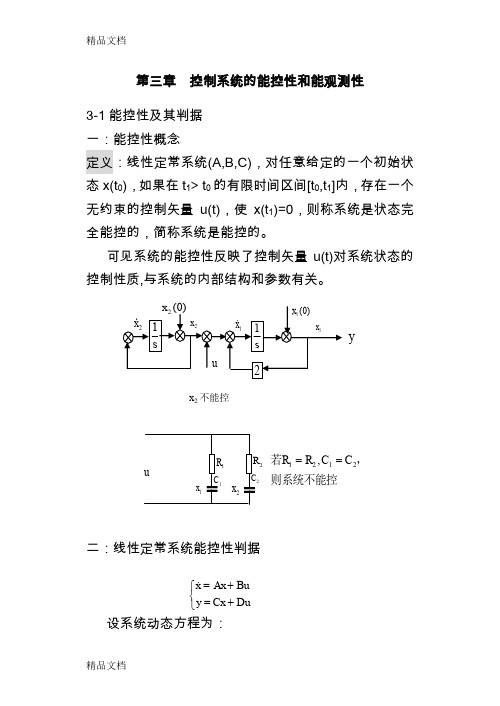
第三章 控制系统的能控性和能观测性3-1能控性及其判据 一：能控性概念定义：线性定常系统(A,B,C)，对任意给定的一个初始状态x(t 0)，如果在t 1> t 0的有限时间区间[t 0,t 1]内，存在一个无约束的控制矢量u(t)，使x(t 1)=0，则称系统是状态完全能控的，简称系统是能控的。
可见系统的能控性反映了控制矢量u(t)对系统状态的控制性质,与系统的内部结构和参数有关。
二：线性定常系统能控性判据设系统动态方程为：x 2不能控y2则系统不能控，若2121,C C R R ==⎩⎨⎧+=+=DuCx y Bu Ax x设初始时刻为t 0=0，对于任意的初始状态x(t 0)，有： 根据系统能控性定义，令x(t f )=0，得：即：由凯莱-哈密尔顿定理：令 上式变为：对于任意x(0),上式有解的充分必要条件是Q C 满秩。
判据1：线性定常系统状态完全能控的充分必要条件是：⎰-+=ft f f f d Bu t x t t x 0)()()0()()(τττφφ⎰⎰---=--=-ff t f f t f f d Bu t t d Bu t t x 01)()()()()()()0(τττφφτττφφ⎰--=f t d Bu x 0)()()0(τττφ∑-=-==-1)()(n k kk A A eτατφτ∑⎰⎰∑-=-=-=-=101)()()()()0(n k t k k t n k k k ff d u B A d Bu A x ττταττταkt k u d u f=⎰)()(ττταUQ u u u u B A B A AB B Bu A x c k n n k kk -=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-=--=∑ 321121],,,[)0(能控性矩阵Q C =[B ，AB ，A 2B ，…A n-1B]满秩。
对于单输入系统，Q C =[b ，Ab ，A 2b ，…A n-1b] 如果系统是完全能控的，称（A 、B ）或（A 、b ）为能控对。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n1 + n2 = rank ⎡ ⎣B
第五章 能控性、能观性与 传递函数
马树萍
§5.1 线性定常系统的结构分解
§5.1-1 不完全能控不完全能观系统的结构分解 考虑线性定常系统 (5.1.1) x = Ax + Bu , y = Cx x 为 n 维状态向量，u 为 p 维输入向量，y 为 q 维 A, B, C 分别为 n × n, n × p, n × q 维的实常阵。 输出向量， 问题： 若 ( A, B, C ) 同时为不完全能控不完全能观的，是否可通 过引进非奇异线性变换，将其能控能观部分与不能控不能 观部分及能控不能观，不能控能观部分同时分离呢？ 答案是肯定的
n1 , n2 , n3 , n4 维分状态, 联合(5.1.8)－(5.1.10)即有系统 ˆ 下, 结构形式为(5.1.2)。 (5.1.1)在非奇异线性变换 x = Tx
10
§5.1-1 不完全能控不全能观系统的结构分解
⎡ A11 下面证明 ( ⎢ ⎣0 A12 ⎤ ⎡ B1 ⎤ , ⎢ ⎥ ) 能控。因为 ⎥ A22 ⎦ ⎣ B2 ⎦
⎡ F1T ⎤ ⎢ T⎥ F2 ⎥ −1 ⎢ T = T ⎢ F3 ⎥ ⎢ T⎥ ⎢ ⎣ F4 ⎥ ⎦
(5.1.4)
6
§5.1-1 不完全能控不完全能观系统的结构分解
F1T T2 = 0, F1T T3 = 0, F1T T4 = 0 F2T T1 = 0, F2T T3 = 0, F2T T4 = 0 F3T T1 = 0, F3T T2 = 0, F3T T4 = 0 F4T T1 = 0, F4T T2 = 0, F4T T3 = 0
7
§5.1-1 不完全能控不完全能观系统的结构分解
ˆ. 对系统(5.1.1)作非奇异线性变换 x = Tx
由 X C , X No 是 A 的不变子空间, AT1 , AT2 各列仍属于 X C , AT1 , AT3 各列仍属于 X No , 及 (5.1.6),(5.1.7)推得
⎡ F1T AT1 ⎢ T F2 AT1 −1 ⎢ ˆ A = T AT = T ⎢ F3 AT1 ⎢ T ⎢ ⎣ F4 AT1 F1T AT2 F2T AT2 F3T AT2 F4T AT2 F1T AT3 F2T AT3 F3T AT3 F4T AT3 F1T AT4 ⎤ ⎥ F2T AT4 ⎥ F3T AT4 ⎥ ⎥ T F4 AT4 ⎥ ⎦
n4 = n − (n1 + n2 + n3 ),
5
§5.1-1 不完全能控不完全能观系统的结构分解
T = [T1 T2 T3 T4 ]
分析 T −1 的性质。
(5.1.3)
F1 , F2 , F3 , F4 分别为 n × n1 , n × n2 , n × n3 , n × n4 维矩阵。 由 T −1T = I 推得：
3
A12 A22 0 0
A13 0 A33 0
A14 ⎤ ⎡ x1 ⎤ ⎡ B1 ⎤ ⎢ x ⎥ ⎢B ⎥ A24 ⎥ ⎥ ⎢ 2⎥ + ⎢ 2⎥u A34 ⎥ ⎢ x3 ⎥ ⎢ 0 ⎥ ⎥⎢ ⎥ ⎢ ⎥ A44 ⎦ ⎣ x4 ⎦ ⎣ 0 ⎦
§5.1-1 不完全能控不完全能观系统的结构分解
⎡ x1 ⎤ ⎢x ⎥ y = [ 0 C2 0 C4 ] ⎢ 2 ⎥ ⎢ x3 ⎥ ⎢ ⎥ 并且： x 4⎦ ⎣ ⎡ A11 A12 ⎤ ⎡ B1 ⎤ (1) ( ⎢ , ⎢ ⎥ ) 能控， ⎥ ⎣ 0 A22 ⎦ ⎣ B2 ⎦ ⎡ A22 A24 ⎤ (2) ( ⎢ , [C2 C4 ]) 能观， ⎥ ⎣ 0 A44 ⎦
2
§5.1-1 不完全能控不完全能观系统的结构分解 定理5.1（Kalman规范分解定理） 对不完全能控不完全 能观系统(5.1.1), 通过非奇异线性变换可实现系统结构的 规范分解, 其规范分解的表达式
⎡ x1 ⎤ ⎡ A11 ⎢x ⎥ ⎢ 0 ⎢ 2⎥ = ⎢ ⎢ x3 ⎥ ⎢ 0 ⎢ ⎥ ⎢ ⎣ x4 ⎦ ⎣ 0
8
§5.1-1 不完全能控不完全能观系统的结构分解
⎡ A11 A12 A13 A14 ⎤ ⎢0 A ⎥ 0 A 22 24 ⎥ =⎢ ⎢0 0 A33 A34 ⎥ ⎢ ⎥ 0 0 A44 ⎦ ⎣0 由 B 的各列属于 X C 及(5.1.7)推得: ⎡ F1T B ⎤ ⎡ B1 ⎤ ⎢ T ⎥ ⎢ ⎥ F2 B ⎥ ⎢ B2 ⎥ −1 ⎢ ˆ B =T B = T = ⎢ F3 B ⎥ ⎢ 0 ⎥ ⎢ T ⎥ ⎢ ⎥ ⎢ ⎣ F4 B ⎥ ⎦ ⎣0⎦
(5.1.5a) (5.1.5b) (5.1.5c) (5.1.5d)
由 (5.1.5b), (5.1.5d), F2 , F4 的各列与 X No 的基底正交， 故 F2 ∈ X O , F4 ∈ X O (5.1.6) 由(5.1.5c), (5.1.5d), F3 , F4 的各列与 X C 的基底正交，故 F3 ∈ X Nc , F4 ∈ X Nc (5.1.7)
4
(3)
(5.1.2)
( A22 , B2 , C2 ) 能控能观。
§5.1-1 不完全能控不完全能观系统的结构分解 证明：选取变换矩阵。 取
T1 为 n × n1 维矩阵,其列构成子空间 X C ∩ X No 的基底；
T2 为 n × n2 维矩阵,其列构成子空间 X C − X C ∩ X No 的基底； T3 为 n × n3 维矩阵,其列构成子空间 X No − X C ∩ X No 的基底。 则 T1 , T2 , T3 的各列线性无关, 且 n1 + n2 + n3 ≤ n. T4 为 n × n4 维 使 [T1 T2 T3 T4 ] 为非奇异矩阵的任意 矩阵。
(5.1.8)
(5.1.9)
9
§5.1-1 不完全能控不完全能观系统的结构分解 由 C T 的各列属于 X O 推得
ˆ = CT = [CT CT C 1 2 CT3 CT4 ] = [ 0 C2
T 4 T
0 C4 ] (5.1.10)
ˆ=⎡ 令x ⎣x
T 1
x
T 2
x
T 3
x ⎤ ⎦ , x1 , x2 , x3 , x4 分别为