锐角三角形费马点的作法
三角形 几何 费马点

三角形几何费马点
费马点,又称斯泰纳点,是指在三角形中,使得三角形内任意两点到该点的距离之和最短的点。
费马点是三角形的一个重要几何概念,具有广泛应用。
在三角形中,费马点也可以被定义为使得三角形内任意两点到该点的距离之和最大的点。
费马点的求解方法有多种,其中最常用的是通过构造等边三角形来确定费马点的位置。
具体来说,可以将三角形中的每个角度构造一个等边三角形,然后将这些等边三角形连接起来,得到一个正三角形。
该正三角形的中心即为费马点。
费马点有着许多有趣的性质,例如:
1.费马点和三角形的其他重要点(重心、垂心、外心、内心)构成的四边形是一个菱形。
2.费马点到三角形三边的距离相等。
3.在任意三角形中,费马点、重心、垂心、外心、内心都在一条直线上,这条直线称为欧拉线。
通过研究费马点及其相关性质,可以深入理解三角形的几何性质,为解决三角形相关问题提供帮助。
- 1 -。
费马点做法依据

费马点做法依据
皮埃尔·德·费马,法国律师和业余数学家。
他在数学上的成就不比职业数学家差,他似乎对数论最有兴趣,亦对现代微积分的建立有所贡献。
被誉为“业余数学家之王”。
费马,是当今常见译法,也翻译作费尔马。
80年代的书籍文章也多见译为“费尔玛”的情况,但“费玛”则少见。
费尔马点:
如果存在一个点到三角形三个顶点的距离之和为最小,则这个点称为费尔马点。
证明:
情况一:当△ABC最大内角小于120°时
以C点为旋转中心,将△CDB逆时针旋转60度到△CEF 位置。
易知DB=EF,DC=CE=DE,DA+DB+DC=DA+DE+EF,显然当A、D、E、F四点共线时,距离之和最短。
当A、D、E共线时,
∠CDA=120°,当D、E、F共线时,∠FEC=∠BDC=120°,所以D点应该对三个顶点的张角都为120°,这就是费尔马点的位置。
情况二:当△ABC有一内角不小于120°时:
很显然此时点C就是费马点,由此可知如果三角形有一个内角大于等于120°时,费马点就是该内角顶点。
综上所得:我们知道,当△ABC最大内角小于120°时,F 在△ABC内部,且满足∠BFC=∠CFA=∠AFB=120°;当△ABC有一内角不小于120°时,F点与最大角的顶点重合。
费马点证明过程

费马点证明过程
费马点,也称为费马-托里拆利点,是在一个三角形内部的一个特殊点,从该点到三角形的三个顶点的距离之和最小。
这个点在三角形中的位置依赖于三角形的形状:在锐角三角形中,它位于三角形内部;在直角三角形中,它与直角顶点重合;在钝角三角形中,它位于三角形外部。
费马点的证明过程相对复杂,以下是其基本思路:
首先,考虑一个锐角三角形ABC。
假设P是三角形ABC内的任意一点。
不失一般性,我们可以假设角A是最小的角。
我们将三角形BPC绕点B旋转60度,使得BC与BA重合,得到新的点P'。
此时,点P'位于线段AP的延长线上。
然后,我们注意到三角形BPP'是一个等边三角形,所以BP=PP'。
因此,AP+BP+CP=AP+PP'+CP。
由于PP'+CP>PC',我们得到AP+BP+CP>AP+PC'。
这表明,点P到三角形三个顶点的距离之和大于点A到三角形三个顶点的距离之和。
同理,我们可以证明对于三角形内的任意点P,其到三角形三个顶点的距离之和都大于点A到三角形三个顶点的距离之和。
因此,点A就是使得距离和最小的点,也就是费马点。
对于直角三角形和钝角三角形,我们可以使用类似的方法进行证明,只是旋转的角度和点的位置会有所不同。
这个证明过程利用了三角形的性质和几何变换,展示了费马点的存在性和唯一性。
同时,它也展示了数学证明中的严谨性和创造性。
三角形费马点的证明

三角形费马点的证明费马点是指在一个三角形中,使得从该点到三角形的三个顶点的距离之和最小的点。
现在我们来证明费马点的存在性和唯一性。
我们先来看费马点的存在性。
设三角形的三个顶点分别为A、B、C,我们要证明存在一个点P,使得PA + PB + PC的和最小。
假设P点不在三角形内,而在三角形的外部某个位置。
我们可以通过以下步骤来构造一个在三角形内的点P',使得P'A + P'B + P'C 的和小于PA + PB + PC的和。
我们将三角形ABC的边AB和边AC的中垂线分别延长至点D和E。
然后,我们以D为圆心,AB的长度为半径作一个圆,以E为圆心,AC的长度为半径作一个圆。
这两个圆将会在点F相交。
现在,我们来比较两个三角形PAB和P'AF。
根据三角形的性质,我们知道P'AF的边长之和小于PAB的边长之和,即P'A + AF < PA + AB。
同理,我们可以比较三角形PAC和P'AE,以及三角形PBC和P'BF。
根据上述比较过程,我们可以得出以下结论:P'A + AF < PA + ABP'B + BF < PB + BCP'C + CE < PC + CA现在,我们将点F作为新的点P',根据上述不等式可以得出以下结论:P'A + P'B + P'C = P'A + AF + P'B + BF + P'C + CE < PA + AB + PB + BC + PC + CA = PA + PB + PC因此,P'点满足P'A + P'B + P'C的和小于PA + PB + PC的和,这与假设矛盾。
所以,我们可以得出结论:费马点一定存在于三角形的内部。
接下来,我们来证明费马点的唯一性。
假设存在两个费马点P和Q,我们要证明P和Q重合。
三角形费马点的证明及应用

三角形费马点的证明及应用费马点是指在平面上的任意三个不共线的点A、B、C中,使得∠ABC、∠ACB 和∠BAC的三个角的和最小的点。
费马点也称为斯纳尔·费马点,他是17世纪法国数学家斯纳尔·费马所研究的最小角三个角的位置问题。
为了证明费马点的存在,我们可以利用极限的思想进行推导。
首先假设在AB上存在一个点X使得∠CAX为等腰三角形CAX的顶角。
那么我们可以构造一个角为∠XAC的等腰三角形XAC。
显然,∠BAX=∠XAC,那么由三角形外角和定理可知∠ABC+∠AXC=180度。
由于AX是由三角形外一点引出的两条射线,所以AXC>180度,所以∠ABC<∠BAC。
同理,我们可以得到两个不等式:∠BAC<∠BCA,∠BCA<∠CAB。
将这三个不等式相加得到:∠ABC+∠BAC+∠BCA<∠ABC+∠BAC+∠CAB。
即∠ABC+∠BAC+∠BCA的和是最小的三个角的和。
我们可以进一步构造一个点P,在平面上使得∠BAP=∠BCP=∠CAP,即三角形ABP、BCP和CAP是等腰三角形。
由于三个等腰三角形所形成的角APB、BPC 和CPA的和一定是最小的,所以∠ABC+∠BAC+∠BCA的和一定是∠APB+∠BPC+∠CPA的和的一个下界。
我们可以发现,当P点与三角形ABC的内角A,B,C重合时,三角形ABP、BCP 和CAP都是等边三角形,此时∠APB+∠BPC+∠CPA=360度。
所以,∠ABC+∠BAC+∠BCA的和一定小于等于360度,在平面上一定存在一个点使得∠ABC+∠BAC+∠BCA的和为最小。
这个点就是费马点。
费马点的应用非常广泛,尤其是在物理学和工程学中。
例如,在导弹的航空导航中,费马点可以确定导弹的最短飞行路径,从而最大限度地节省燃料。
在通信网络中,费马点可以确定网络中的最佳传输路径,提高信息传输的效率。
此外,费马点还可以应用于地理学领域,确定地理坐标系统的最佳布局。
初中几何模型:费马点问题的全面分析、处理和归纳,收藏!

初中⼏何模型:费马点问题的全⾯分析、处理和归纳,收藏!
【问题处理】下⾯简单说明如何找点,使它到三个顶点的距离之和最⼩?这就是所谓的费马点问题.
因此,当的每⼀个内⾓都⼩于时,所求的点对三⾓形每边的张⾓都是,可按照如上的办法找到点;当有⼀内⾓⼤于或等于时,所求的点就是钝⾓的顶点.
费马问题告诉我们,存在这么⼀个点到三个定点的距离之和最⼩,解决问题的⽅法是运⽤旋转变换.
【问题归纳】符合条件的点P,我们把它叫做费马点。
所谓的“费马点”就是法国著名业余数学家费马在给数学朋友的⼀封信中提出关于三⾓形的⼀个有趣问题:“在三⾓形所在平⾯上,求⼀点,使该点到三⾓形三个顶点距离之和最⼩.”让朋友思考,并⾃称已经证明了。
这是费马通信的⼀贯作风。
⼈们称这个点为“费马点”。
还有像著名的费马⼤定理(当整数n >2时,关于x, y, z的⽅程 x^n + y^n = z^n 没有正整数解。
)也是这样,给欧拉的信中提出的,⾃称已经“有了⾮常巧妙的证明”。
直到离开也没告诉⼈家这个所谓证明,结果困扰世界数学界三百多年。
费马点就是到三⾓形的三个顶点的距离之和最⼩的点.费马点结论:对于⼀个各⾓不超过120°的三⾓形,费马点是对各边的张⾓都是120°的点;对于有⼀个⾓超过120°的三⾓形,费马点就是这个内⾓的顶点.
【综合应⽤】
中考真题1:
【答案解析】
中考真题2:【答案解析】。
三角形的费马点问题
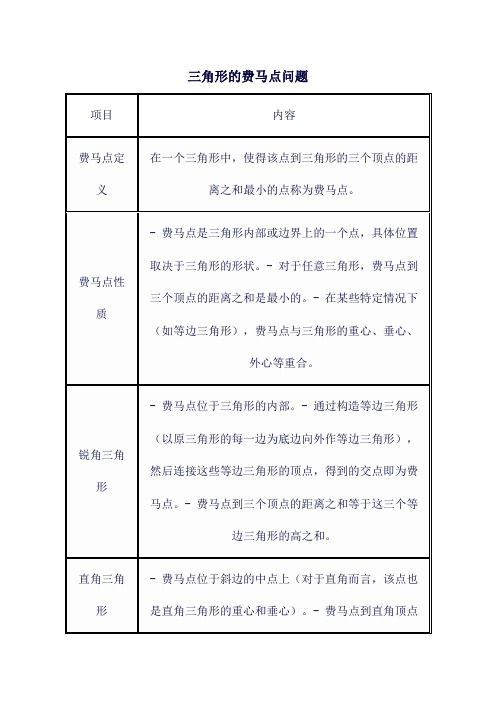
项目
内容费马Βιβλιοθήκη 定义在一个三角形中,使得该点到三角形的三个顶点的距离之和最小的点称为费马点。
费马点性质
- 费马点是三角形内部或边界上的一个点,具体位置取决于三角形的形状。- 对于任意三角形,费马点到三个顶点的距离之和是最小的。- 在某些特定情况下(如等边三角形),费马点与三角形的重心、垂心、外心等重合。
钝角三角形
- 费马点位于三角形的外部,且位于钝角的补角所对应的边的垂直平分线上。- 通过构造以钝角顶点为顶点的两个等腰三角形(腰长等于原三角形的钝角两边),然后连接这两个等腰三角形的底边中点,得到的交点(在三角形外部)即为费马点。- 费马点到三个顶点的距离之和等于这两个等腰三角形的腰长之和减去钝角两边之差(或加上它们的和,但通常我们关注的是减去的情况,因为费马点是使距离和最小的点)。
锐角三角形
- 费马点位于三角形的内部。- 通过构造等边三角形(以原三角形的每一边为底边向外作等边三角形),然后连接这些等边三角形的顶点,得到的交点即为费马点。- 费马点到三个顶点的距离之和等于这三个等边三角形的高之和。
直角三角形
- 费马点位于斜边的中点上(对于直角而言,该点也是直角三角形的重心和垂心)。- 费马点到直角顶点的距离等于斜边的一半,到另外两个顶点的距离之和等于斜边的另一半加上直角边之差(或和,取决于具体直角三角形的边长关系)。
特殊情况
- 对于等边三角形,费马点与重心、垂心、外心等重合,位于三角形的中心。- 对于等腰三角形,费马点位于底边的垂直平分线上,且到两个底边顶点的距离相等。
三角形费马点的证明

三角形费马点的证明费马点是指平面上的一个点,它到三角形的三个顶点的距离之和最小。
这个问题最早由法国数学家费马在17世纪提出,并且给出了一个简洁而美观的证明。
我们先来看一个特殊的情况,当三角形是等边三角形时,费马点就是三角形的重心。
重心是指三角形三条中线的交点,它到三个顶点的距离之和是最小的。
这个结论是很容易证明的,因为等边三角形的三个顶点到重心的距离都是相等的,所以它们的距离之和一定是最小的。
然而,当三角形不是等边三角形时,费马点的位置就不那么容易确定了。
我们可以通过以下步骤来证明费马点的存在,并且给出一个简单的构造方法。
我们将三角形的一条边延长,然后以这条边为直径画一个圆。
然后,我们再以另外两条边的延长线为切线,将圆与两条延长线相切于点A和点B。
接下来,我们连接点A和点B,并将这条线段的中点记为点C。
根据切线定理,我们知道切线与半径的垂线相互垂直。
所以,线段AC和线段BC与圆的切点A和B相互垂直。
而根据垂线定理,垂线的长度最短,所以线段AC和线段BC是与圆相切的两条线段中最短的。
现在我们来证明一下,点C就是三角形费马点的位置。
假设点C不是费马点,而是另外一个点D。
那么,三角形的三个顶点A、B和D 之间的距离之和一定小于三角形的三个顶点A、B和C之间的距离之和。
我们可以通过以下步骤来证明这一点。
首先,连接点A和点D,并延长线段AD,将圆与延长线段相交于点E。
然后,连接点B和点D,并延长线段BD,将圆与延长线段相交于点F。
现在我们来比较一下线段AE、线段CF和线段BC的长度。
根据切线定理,线段AE和线段BD是最短的。
而线段CF是线段AE和线段BD 的一条中线,根据中线定理,线段CF的长度一定小于等于线段AE 和线段BD的长度。
所以,线段CF的长度一定小于等于线段BC的长度。
同样的道理,我们可以比较一下线段BF、线段DE和线段AC的长度。
根据切线定理,线段BF和线段DE是最短的。
而线段AC是线段BF 和线段DE的一条中线,根据中线定理,线段AC的长度一定小于等于线段BF和线段DE的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一道竞赛题,在、锐角三角形ABC中,求得一点P,使PA+PB+PC最短并证明
(1)分别以AB,AC为一边,向△ABC外作正△ABC'和正△ACB'.连结BB',CC'.设锐角△ABC。
线段BB'与CC'交于点P.易知,点P即是费尔马点,且BB'=CC'=PA+PB+PC.(这里,你讲明了不用证明)。
下面的工作即是证明线段BB'(CC')最短。
(2),设点Q是△ABC内的任一点,连结AQ,BQ,CQ.以线段BQ为一边,向外(点C'方向)作正△BQR,连结RC'.易知,∠C'BR+∠RBA=∠C'BA=60°=∠RBQ=∠RBA+∠ABQ,===>∠C'BR=∠ABQ,,又显然有C'B=AB,RB=QB.====>△C'BR≌△ABQ(S.A.S)===>C'R=AQ.====>折线C'RQC=AQ+BQ+CQ.又折线C'RQC>线段C'C.(连结两点的所有线中,直线段最短)。
====)AQ+BQ+CQ>AP+BP+CP. 这即证明了点P符合题设,最短。
(注:以上仅供你参考。
)
若点P为锐角三角形ABC的费马点,且角ABC=60度,PA=3,PC=4,则PB的值为
从而BP^2=AP*CP,即BP=2√3。
