磁介质
合集下载
电磁学-磁介质
• 磁介质（magnetic medium）：
–对磁场有一定响应,并能反过来影响磁场的物质 –一般物质在较强磁场的作用下都显示出一定程度的磁性，
即都能对磁场的作用有所响应，所以都是磁介质
• 磁化（magnetization）
–在外磁场的作用下，原来没有磁性的物质，变得具有磁 性，简称磁化。磁介质被磁化后，会产生附加磁场，从 而改变原来空间磁场的分布
• 顺磁质的磁化
– 分子在外磁场作用下趋向于外磁场排列 –热运动与磁场作用相抵抗
抗磁质
有外场
m分子0 m分子0
抗磁质
• 抗磁质分子的固有磁矩m分子= ml+ ms＝0 • 不存在由非零的分子固有磁矩规则取向引
起的顺磁效应。磁性来源？
• 抗磁质磁性起源于电子轨道运动在外磁场 下的变化
• 电子轨道运动为什么会变化？原因：在外 磁场下受洛伦兹力
D (1 e )0E
r (1 e )
v
vv
D r0E E
r称为相对电容率
或相对介电常量
例1 一环形螺线管，管内充满磁导率为μ，相对磁导 率为μr的顺磁质。环的横截面半径远小于环的半径。
单位长度上的导线匝数为n。
求：环内的磁场强度和磁感应强度
解：
H dl
L
H 2r
NI
NI
r
H
nI
• 解决的办法——需要补充或附加有关磁介 质磁化性质的已知条件
• 有介质时，第四章中给出的安培环路定理
可理解为
I' M dl
总场
两边同
除以0 ，
再移项
定义： 磁场强度
B dl 0 I 0I0 I'
L
L内
B dl 0 I0 0 M dl
–对磁场有一定响应,并能反过来影响磁场的物质 –一般物质在较强磁场的作用下都显示出一定程度的磁性，
即都能对磁场的作用有所响应，所以都是磁介质
• 磁化（magnetization）
–在外磁场的作用下，原来没有磁性的物质，变得具有磁 性，简称磁化。磁介质被磁化后，会产生附加磁场，从 而改变原来空间磁场的分布
• 顺磁质的磁化
– 分子在外磁场作用下趋向于外磁场排列 –热运动与磁场作用相抵抗
抗磁质
有外场
m分子0 m分子0
抗磁质
• 抗磁质分子的固有磁矩m分子= ml+ ms＝0 • 不存在由非零的分子固有磁矩规则取向引
起的顺磁效应。磁性来源？
• 抗磁质磁性起源于电子轨道运动在外磁场 下的变化
• 电子轨道运动为什么会变化？原因：在外 磁场下受洛伦兹力
D (1 e )0E
r (1 e )
v
vv
D r0E E
r称为相对电容率
或相对介电常量
例1 一环形螺线管，管内充满磁导率为μ，相对磁导 率为μr的顺磁质。环的横截面半径远小于环的半径。
单位长度上的导线匝数为n。
求：环内的磁场强度和磁感应强度
解：
H dl
L
H 2r
NI
NI
r
H
nI
• 解决的办法——需要补充或附加有关磁介 质磁化性质的已知条件
• 有介质时，第四章中给出的安培环路定理
可理解为
I' M dl
总场
两边同
除以0 ，
再移项
定义： 磁场强度
B dl 0 I 0I0 I'
L
L内
B dl 0 I0 0 M dl
磁介质(Magnetic materials)
1/ 2
于顺外场的增加。 在(i)、(ii)两种情形，电子都获得一个逆外场方向的诱导磁矩(induced 101
5.1 磁化(Magnetization) moment), 用到式(5.2)，有 e e minduced = L= ⋅m r 2 。 2 me 2 me e L 将 L 的表达式代入，得到诱导磁矩的矢量式为 e2 r2 m induced =− B (5.6) 4 me 原子序数为 Z 的原子有 Z 个电子，其轨道半径各不相同，相对于外场 的倾角也各不相同。取平均值，得到每个原子的有效(effective)诱导磁 矩为 e2 m =− Zr 2 B (5.7) 6 me 0 物质的磁化强度(magnetization)为 Ne2 2 M =− Zr B (5.8) 6 me 0
•
•
•
磁化强度(magnetization)： 设物质中的原子在外磁场中磁化后的磁矩为 m。对大量原子的磁矩取平均， 其平均值记为 m 。 定义：磁化强度为单位体积中的原子磁矩的矢量和。 M = N m 。 (5.1) 其中，N 为单位体积中的原子数。磁化强度是描述物质磁化性质的量。
5.1.5 抗磁性(Diamagnetism)
•
原子在外场中的诱导磁矩(induced magnetic moments)：
•
电子的固有角速度(angular velocity)： 设电子在半径 r 的圆轨道以角速度 0 运动。向心加速度为 2 0r , 2 2 向心力为 Ze / 4 0 r ，故有 2 2 2 m e 0 r = Ze / 4 0 r 从而有 Ze2 0= 4 0 me r 3
104
第五章 磁介质(Magnetic materials) 向减少，合成效果为向下的净磁化电流(net magnetic current)。如 Figure 5.8 所示。 如 Figure 5.9, 在磁化体中取一个体积元 = x y z , 其中心点的坐标为 (x, y, z)。类似于螺线管中介质的 M 与 I 的关系 I M = M ，磁化强度矢量 M 的 x, y, z 分量，分别对应于环绕电流 I1, I2, I3。即，将积元 中磁偶极矩 矢量 M , 分解为 x, y, z 分量，与环绕电流 I1, I2, I3 的对应关系分别为 I 1 y z =M x 即 I 1= M x x . (5.16a) 同理，有 I 2= M y y , (5.16b) I 3= M z z . (5.16c) 合成的磁化电流密度 jM，其 z 分量由 I1，I2 贡献而得。如果 I2 沿 x 轴方向变
磁介质
µ = µ0 µr叫磁介质的磁导率。 H 叫磁场强度。 叫磁介质的磁导率。 叫磁场强度。
的环路积分: 考虑 H 的环路积分
H ⋅ dl = ∫ ∫
L
B
µ0 µ r L
⋅ dl =
1
µ0
∫µ
L
B
r
⋅ dl
=
1
µ0
∫B
L
0
⋅ dl = I 0,int
∫ H ⋅ dl = I
L
0 ,int
H 的环路定理
B = B0 + B′ > B0
µr > 1
磁化电流 Is 可产生附加磁场，但无热效应，因为 可产生附加磁场，但无热效应， 无宏观电荷的移动，磁化电流束缚在介质表面上， 无宏观电荷的移动，磁化电流束缚在介质表面上，不 可引出，因此，磁化电流也称为束缚电流 束缚电流。 可引出，因此，磁化电流也称为束缚电流。
µ 当磁介质为铁磁质时， 当磁介质为铁磁质时， r
j' = (µr −1)nI
管内磁场基本上由束缚电流产生， 管内磁场基本上由束缚电流产生，这时的自由电流 往往被叫做励磁电流 励磁电流。 往往被叫做励磁电流。
3.磁场强度矢量及其环路定理。 3.磁场强度矢量及其环路定理。 磁场强度矢量及其环路定理 在真空中的安培环路定理中： 在真空中的安培环路定理中：
2）抗磁质的磁化机制 对抗磁介质来说，无外磁场时， 对抗磁介质来说，无外磁场时， 各电子的磁矩矢量和为 0，分子磁 分子不显磁性。 矩 分子不显磁性。 ∑ m,= 0
B0
ω
v
f核
fL
i
加外磁场后，电子受的向心力 加外磁场后， 为核力和洛仑兹力的叠加， 为核力和洛仑兹力的叠加，
磁介质
B=B+(ralative8以电子的轨道运动为例，第i 个电子受的磁力矩B m M i i v vv ×=电子轨道角动量增量ii i L t M L v v v ⊥=d d ∴电子旋进，它引起的感应磁矩反平行于。
i m Δv0B v 这种效应在顺磁质中也有，不过与分子固有磁矩的转向效应相比弱得多。
m im i11由于介质磁化而出现的一些等效的附加电流分布。
2. 磁化电流如上图，磁介质均匀被磁化，内部各点处的分子电流会相互抵消；表面上的小分子电流没有抵消，它们方向相同，等效为表面上有一层面束缚电流。
Si m v v＝分子以顺磁质为例：由于分子的热运动，每个磁极子的取向不断在变化，但从统计平均的角度，每个磁极子对磁化强度的贡献是一样的, 将这个贡献等效为一分子磁矩，设分子m vM v在磁场中发生磁化，磁化强度MSNΔP m分m r ΔiS Ni分m r 顺磁质抗磁质2rS S i m π=v v 图示为顺磁质情形Mnm VM Vm n VMmM V V V ˆΔˆΔlim limΔ)ˆ(lim0ΔΔ0Δ分分分====→→→∑v14现为面束缚电流。
磁化n rM rt M r lrd SI ′d θ与电介质极化电荷面密度nP ˆ⋅v设：二、环路定理的应用举例[例1]书P171:无限长直螺线管充以磁介质[例2]书P172: 长同轴电缆充以磁介质19SΔS ΔSS Δ<<Δ侧lΔlΔ<<δ(2(当tg tg 211=θμμθ23* 静磁屏蔽铁磁材料的闭合壳体置于外磁场中，壳内口腔中磁感应强度大大削弱的现象。
应用：精密探头、显象管…都需要磁屏蔽。
*铁磁质具有把磁感应线聚集于自己内部的特性(磁感应线沿铁走)部分磁屏蔽25§19.4 铁磁质(ferromagnetic substance)一、磁畴（magnetic domain ）自发磁化的小区域─磁畴实验研究表明：铁磁质内部存在一个个小区域，小区域内，分子磁矩有序排列(自发磁化)。
磁场中磁介质
磁介质的分类
顺磁性介质
抗磁性介质
铁磁性介质
反铁磁性介质
在磁场中容易被磁化的 物质，如铝、铂等。
在磁场中不容易被磁化 的物质，如铜、金等。
在磁场中极易被磁化的 物质，如铁、钴、镍等。
在磁场中具有反铁磁性 的物质，如锰、铬等。
02
磁场对磁介质的影响
磁场对磁介质的作用
磁化现象
磁场对磁介质产生作用，使其内 部磁矩定向排列，形成磁化现象。
剩余磁化强度
当磁场去除后，磁介质仍会保留一部分磁化强度， 称为剩余磁化强度。
磁介质的磁导率
相对磁导率
描述磁介质在磁场中的导磁能力与真空导磁能 力的比值。
最大磁导率
在一定磁场强度下，磁介质的磁导率达到最大 值。
温度系数
表示磁导率随温度变化的系数，某些材料的温度系数较大，对温度变化较为敏 感。
03
磁介质的性质与特点
磁滞现象
磁介质在磁化过程中会出现滞后现 象，即当磁场反向时，磁介质的磁 化强度不会立即消失，而是逐渐减 小。
磁损耗
在交变磁场中，磁介质会因为磁滞 现象和涡流效应产生能量损耗。
磁介质的磁化过程
起始磁化
磁介质在磁场中开始被磁化的过程，起始磁化曲 线通常是非线性的。
磁饱和
随着磁场强度的增加，磁介质的磁化强度逐渐达 到饱和状态，此时磁导率不再变化。
3
磁滞损耗
由于磁滞现象产生的能量损耗，通常表现为热量。
磁介质的损耗特性
介电损耗
01
由于电场作用在磁介质上产生的能量损耗，通常表现为热量。
涡流损耗
02
由于磁场变化产生的涡旋电流在磁介质中产生的能量损耗，通
常表现为热量。
磁介质
这时 满足的运动学方程为
Ze2 2 e rB m r 2 4 0 r
v
' m
同向时
当B不太大时，
0 , 0 20
2 2
eB 由此解得 2m
当 // B 时，也可以得到上述表达式
即 的方向总是与外磁场 B的方向相同。
0 B H M
M ) dl I
L
0
0 S ( 0 E P ) dS q S D 0E P
S
0
L H dl I
L
D dS e dV
S V
B , H , M 之间的关系
（4）超导体
r 0
B0
1933年，迈斯纳和奥克森菲尔德两位科学家发现，如果把超 导体放在磁场中冷却，则在材料电阻消失的同时，磁感应线将 从超导体中排出，不能通过超导体，这种现象称为抗磁性。
由于 r 与1相差甚微，为使用方便，故引入磁介 质的磁化率 m
r 1 m
r 1 e
L
B dl 0 I 0 I s
L L
磁介质中的 安培环路定理
电介质中的 高斯定理
L B dl 0 I 0 L M dl
L ( B
L
1 ' S E dS (q qi ) 0 S 1 1 S E dS q S P dS
Is
I0
Is——磁化电流 js——沿轴线单位长度上的磁 化电流（磁化面电流密度）
3、磁化强度和磁化电流密度之间的关系：
以长直螺线管中的圆柱形磁介质来说明它们的关系。
Ze2 2 e rB m r 2 4 0 r
v
' m
同向时
当B不太大时，
0 , 0 20
2 2
eB 由此解得 2m
当 // B 时，也可以得到上述表达式
即 的方向总是与外磁场 B的方向相同。
0 B H M
M ) dl I
L
0
0 S ( 0 E P ) dS q S D 0E P
S
0
L H dl I
L
D dS e dV
S V
B , H , M 之间的关系
（4）超导体
r 0
B0
1933年，迈斯纳和奥克森菲尔德两位科学家发现，如果把超 导体放在磁场中冷却，则在材料电阻消失的同时，磁感应线将 从超导体中排出，不能通过超导体，这种现象称为抗磁性。
由于 r 与1相差甚微，为使用方便，故引入磁介 质的磁化率 m
r 1 m
r 1 e
L
B dl 0 I 0 I s
L L
磁介质中的 安培环路定理
电介质中的 高斯定理
L B dl 0 I 0 L M dl
L ( B
L
1 ' S E dS (q qi ) 0 S 1 1 S E dS q S P dS
Is
I0
Is——磁化电流 js——沿轴线单位长度上的磁 化电流（磁化面电流密度）
3、磁化强度和磁化电流密度之间的关系：
以长直螺线管中的圆柱形磁介质来说明它们的关系。
第十二章 磁介质
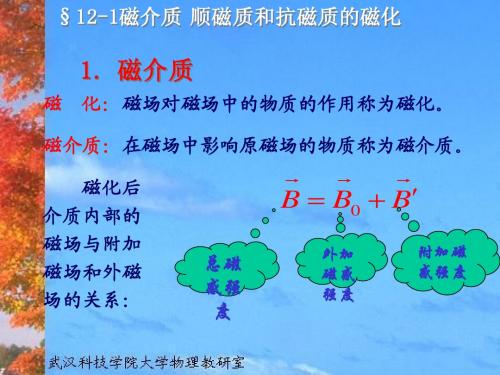
B B0 顺磁质(锰、铬、铂、氧、氮等)
B B0 抗磁质(铜、铋、硫、氢、银等)
B B0 铁磁质(铁、钴、镍等)
在介质均匀充满 磁场的情况下
定义
r
B B0
r
1 1 1
顺磁质 抗磁质 铁磁质
相对 磁导率
2. 分子电流和分子磁矩
分子电流：把分子或原子看作一个整体，分子 或原子中各个电子对外界所产生磁效应的总和，可 用一个等效的圆电流表示，统称为分子电流。 分子磁矩：把分子所具有的磁矩统称为分子磁 矩，用符号 pm 表示。 子中和每个电子相联系的磁矩都受到磁力矩的作用， 由于分子或原子中的电子以一定的角动量作高速转 动，这时，每个电子除了保持环绕原子核的运动和 电子本身的自旋以外，还要附加电子磁矩以外磁场 方向为轴线的转动，称为电子的进动。
或
(
B
0
M ) dl
I
磁介质中的安培环路定理
定义 H
M为磁场强度 0 B ( M ) dl
B
0
I
有磁介质时的 安培环路定理
则
H dl
I
磁介质中的安培环路定理： 磁场强度沿任
意闭合路径的线积分等于穿过该路径的所有传导电 流的代数和，而与磁化电流无关。 表明：磁场强度矢量的环流和传导电流I有关， 而在形式上与磁介质的磁性无关。其单位在国际单 位制中是A/m.
m
§12-2 磁化强度 1. 磁化强度
磁化电流
反映磁介质磁化程度(大小与方向)的物理量。 磁化强度：单位体积内所有分子固有磁矩的 矢量和 p 加上附加磁矩的矢量和 p ，称为磁 化强度，用 M表示。
m m
磁介质(Magnetic materials)
•
对 BM 大小的估计： 用(5.12)式，近似认为 B = B0，有 2 2 m e B M =0 N − Z r2 B 。 3 kT 6 me 0 0 括号中第项为主，忽略第二项，得 B M 0 N m2 。 = B0 3 kT 在室温下，上式约等于 10－4, 说明顺磁效应很弱。
{
}
•
磁化电流密度 (magnetization current density)： 如果介质内磁化不均匀(non-uniform), 会出现磁化体电流, 用磁化电流密度 j M 描述. 如 Figure 5.7，磁化物质中的一块体积，其中磁化强度在 y, z 方向均匀，而 沿 x 方向减少。若将磁化等效为环绕原子的电流，电流环中的电流 I 沿 x 方
5.2 介质中的宏观磁场(The macroscopic magnetic field inside media)
•
介质中的宏观磁场是微观磁场在宏观 小体积内的平均值。介质中的磁场是 真空中（介质不存在时）的磁场 B0 和 介质中的磁化场 BM 二者的矢量叠加。 B = B 0 B M (4.13) 对于顺磁性物质，原子的磁矩沿外场 方向排列，使介质内的磁场增强。 对于抗磁性物质，原子的磁矩逆外场 方向排列，使介质内的磁场减弱。 Figure 5.6
铁磁性(Ferromagnetism)
某些物质，如铁、钴、镍，和某些合金，有很大的固有顺磁效应，称为铁 磁物质。在居里温度(Curie temperature)之下，铁磁物质中在宏观尺度的区 域(domains)内，导电电子的自旋磁矩全部平行排列(align parallel)。这样的 区域称为磁畴，其大小约为 10－10 到 10－12 m3。在无外磁场时，磁畴的取向 (orientation)是随机的(random)，整体不表现磁性。在有外场(external field)时， 有一沿外场方向的净取向，表现出很强的磁性。
对 BM 大小的估计： 用(5.12)式，近似认为 B = B0，有 2 2 m e B M =0 N − Z r2 B 。 3 kT 6 me 0 0 括号中第项为主，忽略第二项，得 B M 0 N m2 。 = B0 3 kT 在室温下，上式约等于 10－4, 说明顺磁效应很弱。
{
}
•
磁化电流密度 (magnetization current density)： 如果介质内磁化不均匀(non-uniform), 会出现磁化体电流, 用磁化电流密度 j M 描述. 如 Figure 5.7，磁化物质中的一块体积，其中磁化强度在 y, z 方向均匀，而 沿 x 方向减少。若将磁化等效为环绕原子的电流，电流环中的电流 I 沿 x 方
5.2 介质中的宏观磁场(The macroscopic magnetic field inside media)
•
介质中的宏观磁场是微观磁场在宏观 小体积内的平均值。介质中的磁场是 真空中（介质不存在时）的磁场 B0 和 介质中的磁化场 BM 二者的矢量叠加。 B = B 0 B M (4.13) 对于顺磁性物质，原子的磁矩沿外场 方向排列，使介质内的磁场增强。 对于抗磁性物质，原子的磁矩逆外场 方向排列，使介质内的磁场减弱。 Figure 5.6
铁磁性(Ferromagnetism)
某些物质，如铁、钴、镍，和某些合金，有很大的固有顺磁效应，称为铁 磁物质。在居里温度(Curie temperature)之下，铁磁物质中在宏观尺度的区 域(domains)内，导电电子的自旋磁矩全部平行排列(align parallel)。这样的 区域称为磁畴，其大小约为 10－10 到 10－12 m3。在无外磁场时，磁畴的取向 (orientation)是随机的(random)，整体不表现磁性。在有外场(external field)时， 有一沿外场方向的净取向，表现出很强的磁性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如果将一个作轨道运动的电子放在外磁场 B0 中， 电子轨道运动的等效电流在磁场中受到磁力矩 M l B0 根据角动量定理 dL Mdt ( l B0 )dt e ( L B0 )dt 2m 上式表明：dL 垂直于 L 和 B0组成的平面
超导体的抗磁性可用下面的动画来演示，小球 是用超导态的材料制成的，由于小球的抗磁性，小 球被悬浮于空中，这就是所说的磁悬浮。
左上图是小磁铁悬浮在 Ba-La-Cu-O 体圆片（浸在液氮中）上方的照片。
超导
三、磁介质中的安培环路定理 如果在通电长螺线管中插入磁介质
I
B
按照安培的分子环流假说理解，介质的磁化过 程类似在其表面感应出“磁化电流”。
H
B
0 r
B
0 r —介质的磁导率
单位：安培/米
磁介质中的 安培环路定理
L
L
B dl 0 I 0 I s
电介质中的 高斯定理 1 S E dS 0 (q q)
B dl 0 I 0 M dl
L
S
1 E dS
(
L
B
0
M ) dl I
H
B
S
S 0 0 ( 0 E P ) dS q
q
1
P dS
0
M
D 0E P
L
H dl j f dS
NI H 2 R
测量： 可用霍尔器件在开口处测量 磁感应强度。 因磁感应强度的法向分量在 切口和铁芯中连续，故霍尔器件 在开口处测量的磁感应强度 B也 就是环路中的磁感应强度。
I
结果： 铁磁质的 B～H 关系不是线性关系！
B
r
B~H
r
r ~ H
H
H
B 由 r 可得出 r ~ H曲线 0 H
当全部磁畴都沿外磁 场方向时，铁磁质的磁化 达到饱和状态。饱和磁化 强度等于每个磁畴中原来 的磁化强度，这个值是很 大的，这就是铁磁质磁性 强的原因。
3. 磁化曲线
装置：
用待测的铁磁质（Fe , Ni , Co , 及稀钍族元素的化合物） 为芯制成螺绕环，并且在环上 开一小切口。 原理:
I
当线圈中通以电流（励磁电流） I 时，由安培 环路定理得环内的磁场强度
B B0 B
B B0
3. 抗磁质及其磁化 抗磁质分子的固有磁矩为零
pm 0
在外磁场中，抗磁质分子会产生附加磁矩 pm 可以证明：pm 总是与外磁场反向
电子在磁场中运动的附加磁矩总是削弱外磁场的作用 使
B B0
抗磁性是一切磁介质共同具有的特性。在顺磁 质物质中，同样具有抗磁质效应，只不过这种抗磁 质效应低于顺磁质效应。
故铁磁质的μr 不是常数，它是随 H 的变化而变的
4. 磁滞回线
Байду номын сангаас和磁感应强度 剩磁 矫顽力
BS .
Br
初始磁 化曲线
HS
.
HC
.
HS
BS
磁滞回线─表明介质的磁化是 不可逆过程 B 的变化落后于H ，从而具 有剩磁，即磁滞效应。每个H 对 应不同的B 与磁化的历史有关。
Hc
B
Br
③
④
能产生特别强的附加磁场，使铁磁质中的磁场 增强102~104倍。 铁磁质的磁导率不是恒量，而是随所在处的磁 场H 而变。 铁磁质的磁化具有磁滞现象。在外磁场撤消后， 铁磁质仍能保持原有的部分磁性。
铁磁质具有一临界温度称为居里点，在居里点， 磁性发生突变。
临界温度（铁磁质的居里点）
每种磁介质当温度升高到其居里点时，高磁 导率、磁滞、磁致伸缩等一系列特殊状态全部消 失，而变为顺磁性。 不同铁磁质具有不同的转变温度居里点
R
I
0
Ir B H 2 R 2
H
r
H
I R
I 2R
0
o
B
R
r
H
r
I 2R
0 I 2 R
r R H 2r I
r
H I 2 r
o
R
在分界面上 H 连续 B 不连续
0 I B 2 r
四、 铁磁质 铁磁质对外磁场的影响最大，它的应用也最广 泛。特别是在信息的记录和存储方面（磁带、计算 机存储器），有着重要意义。 1. 铁磁质的特性 ① ②
显示磁畴结构的铁粉图形
三种铁磁性物质的磁畴
纯铁
硅铁
钴
Si-Fe单晶(001)面的磁畴结构
箭头表示磁化方向
在无外磁场的作用下磁畴取向平均抵消，能量 最低，不显磁性； 在外磁场较弱时，自发磁化方向与外磁场方向 相同或相近的那些磁畴逐渐增大（畴壁位移）；
在外磁场较强时，磁畴自发磁化方向作为一个 整体，不同程度地转向外磁场方向；
这时取安培环路abcda如图
d
B
h
a
b
I
c
磁感应强度对闭合回路 L 的线积分，等于穿过 以 L 为周界的任意曲面上的电流（包括自由电流 I0 和磁化电流 Is ）的代数和。
L
B dl 0 ( I 0 I s )
为了避开处理磁化电流的麻烦，类比电介质中 我们避开对束缚电荷的处理的相同办法，引入辅助 矢量
l 1 , s1 l 2 , s 2
矢量和
原子磁矩 pmi
分子磁矩—— 所有原子磁矩的总和 pm pmi
i
抗磁质 顺磁质
pm 0 pm 0
无外场作用时，对外不显磁性
无外场作用时，由于热运动，
对外也不显磁性 分子磁矩
附加磁矩又称为感应磁矩
电子的拉莫进动 与陀螺在重力场中的 进动完全类似。
力矩的出现，使 角动量发生变化。
mg
L
M dL
角动量增量的方向在力矩方向上，它始终垂 直于角动量。
抗磁质效应的简略解释
当外场方向与原子磁矩同方向时
fm
B0
pm
o r
pm ( pm )
r
o
例题2 ：
普通物理学教案
一无限长载流圆柱体，通有电流 I ，设 电流均匀分布在整个横截面上。柱体的磁导 率为μ，柱外为真空。求柱内外各区域的磁 场强度和磁感应强度。
解： r R r2 L H dl H 2 r I R 2 I Ir H 2 R 2
I
这就使电子绕核运动的轨道平面产生绕外磁场 方向的进动称为拉莫进动。
电子的拉莫进动
拉莫进动使电子获得了 一个附加的转动，转动角速 度方向沿外磁场方向。
这个附加的转动同样等 效于一个圆电流，从而产生 一个附加的磁矩 pm 。 因电子带负电，故附 加磁矩方向与外磁场方向 相反。
B0
pm
pm
E E0
若介质完全充满外电场，或介质表面为等势面
E E0 / r
介质放入外磁场中，介质磁化 B0 B B0 B
较复杂
若介质完全充满外磁场，或介质界面法线垂直于B0
B r B0
2. 磁介质的分类
抗磁质
r 1
r 1
B B0 B B0
铁—1040K
镍— 631K 钴— 1388K
2. 磁 畴( magnetic domain ) 铁磁性主要来源于电子的自旋磁矩。相邻原子 的电子之间存在着很强的“交换作用”，这是一种 量子效应。在无外磁场作用时，它促使自旋磁矩趋 向能量较低的平行排列状态，形成自发磁化达到饱 和状态的微小区域。这些区域称为磁畴。 多晶磁畴 结构示意图 磁畴的体积约为10－12 ~ 10－8 m3，其中含有约 1017~1021个分子 。可用金相显微镜观测。
BS
抗磁质磁化
在外场作用下，每个分子中的所有电子都产生 感应磁矩 pm
磁介质产生 附加磁场
B B
与外场方向 相反
迈纳斯效应 超导体与理想导体在抗磁性上是不同的。若在 临界温度以上把超导样品放入磁场中，这时样品处 于正常态，样品中有磁场存在。当维持磁场不变而 降低温度，使其进入超导状态时，在超导体表面产 生电流，这电流在样品内部产生的磁场抵消了原来 的磁场，使导体内部的磁感应强度为零。超导体内 部的磁场总为零，这一现象称为迈纳斯效应。 零电阻是超导体的一个基本特性，但超导体的 完全抗磁性更为基本。是否转变为超导态，必须综 合这两种测量结果，才能予以确定。
I
l
l I r 2
实验证明，原子中电子除 了作绕核的轨道运动外，还有 自旋，相应有自旋磁矩
e s S 2m S 为自旋角动量
电子的自旋角动量和自旋磁矩都只能由量子 理论说明，经典理论对其无法解释。
原子磁矩 pmi
轨道磁矩 —电子绕核的轨道运动 自旋磁矩 —电子本身自旋
例题1 ：
普通物理学教案
一环形螺线管，管内充满相对磁导率为 μr 的顺磁质。环的横截面半径远小于环的 半径，单位长度上的导线匝数为 n 。求：环 内的磁场强度和磁感应强度。 解：取同心圆安培环路 由介质中的安培环路定理
L H dl H 2 r NI NI H nI 2r B 0 r H 0 r nI
H B
0 r
─磁场强度
D 0 r E
─电位移
磁介质中的安培环路定理:
L
H dl I 0