磁介质习题与解答
15章磁介质 例题习题

第十五章磁介质例题15-1 顺磁物质的磁导率:(A) 比真空的磁导率略小(B) 比真空的磁导率略大(C) 远小于真空的磁导率(D) 远大于真空的磁导率[ B]例题15-2 用细导线均匀密绕成长为l、半径为a (l >> a)、总匝数为N的螺线管,管内充满相对磁导率为μr的均匀磁介质.若线圈中载有稳恒电流I,则管中任意一点的(A) 磁感强度大小为B = μ0 μ r NI.(B) 磁感强度大小为B = μ r NI / l.(C) 磁场强度大小为H = μ0NI / l.(D) 磁场强度大小为H = NI / l.[ D]例题15-3 置于磁场中的磁介质,介质表面形成面磁化电流,试问该面磁化电流能否产生楞次─焦耳热?为什么?答:不能.因为它并不是真正在磁介质表面流动的传导电流,而是由分子电流叠加而成,只是在产生磁场这一点上与传导电流相似.习题1、磁介质有三种,用相对磁导率μr表征它们各自的特性时,(A) 顺磁质μr >0,抗磁质μr <0,铁磁质μr >>1.(B) 顺磁质μr >1,抗磁质μr =1,铁磁质μr >>1.(C) 顺磁质μr >1,抗磁质μr <1,铁磁质μr >>1.(D) 顺磁质μr <0,抗磁质μr <1,铁磁质μr >0.[ C]2、长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流I通过,其间充满磁导率为μ的均匀磁介质.介质中离中心轴距离为r的某点处的磁场强度的大小H = ;磁感强度的大小B = .I / (2πr) μI / (2πr)3、图示为三种不同的磁介质的B~H关系曲线,其中虚线表示的是B = μ0H的关系.说明各代表哪一类磁介质的B~H关系曲线:a代表 的B~H关系曲线.b代表 的B~H关系曲线.铁磁质顺磁质4、有很大的剩余磁化强度的软磁材料不能做成永磁体,这是因为软磁材料 ;如果做成永磁体.5、如图所示的一细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝.当导线中的电流I为2.0 A时,测得铁环内的磁感应强度的大小B为1.0 T,则可求得铁环的相对磁导率μr为(真空磁导率μ 0 =4π×10-7 T·m·A-1)(A) 7.96×102(B) 3.98×102(C) 1.99×102 (D) 63.3 [ B]。
磁介质习题解答

第十二章 磁介质一 选择题1. 磁介质有三种,用相对磁导率r μ表征它们各自的特征时,( ) A .顺磁质0r >μ,抗磁质0r <μ,铁磁质1r >>μ。
B .顺磁质1r >μ,抗磁质1r =μ,铁磁质1r >>μ。
C .顺磁质1r >μ,抗磁质1r <μ,铁磁质1r >>μ。
D .顺磁质0r >μ,抗磁质0r <μ,铁磁质1r >μ。
解:选(C )2. 关于稳恒磁场的磁场强度H 的下列几种说法中哪个是正确的?( ) A . H 仅与传导电流有关。
B . 若闭合曲线内没有包围传导电流,则曲线上各点的H 必为零。
C . 由于闭合曲线上各点H 均为零,则该曲线所包围传导电流的代数和为零。
D . 以闭合曲线L 为边界的任意曲面的H 通量均相等。
解:由⎰∑=⋅L i I l H d ,H 的环流仅与闭合曲线内的传导电流I 有关,而不是H 仅与传导电流有关,所以A 不对。
同样,若闭合曲线内没有包围传导电流,则H 的环流为零,而不是H 为零,B 不对。
H 通量的正负与环路的积分方向有关,所以H 通量并不相同,D 不对所以选(C )二 填空题1. 一个单位长度上密绕有n 匝线圈的长直螺线管,每匝线圈中通有强度为I 的电流,管内充满相对磁导率为μr 的磁介质,则管内中部附近磁感应强度B 的大小= ,磁场强度H 的大小= 。
解:B =nI r μμ0,H =nI2. 图示为三种不同的磁介质的B-H 关系曲线,其中虚线表示的是B =μ0H 的关系,说明a 、b 、c 各代表哪一类磁介质的B-H 关系曲线:a 代表 的B-H 关系曲线;b 代表 的B-H 关系曲线;填空题2图c 代表 的B-H 关系曲线。
解:铁磁质、顺磁质、抗磁质3. 长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流I 通过,其间充满磁导率为μ的均匀磁介质,介质中离中心轴距为r 的某点处的磁场强度的大小 H = ,磁感应强度的大小B = 。
(完整版)《大学物理》习题册题目及答案第13单元 磁介质
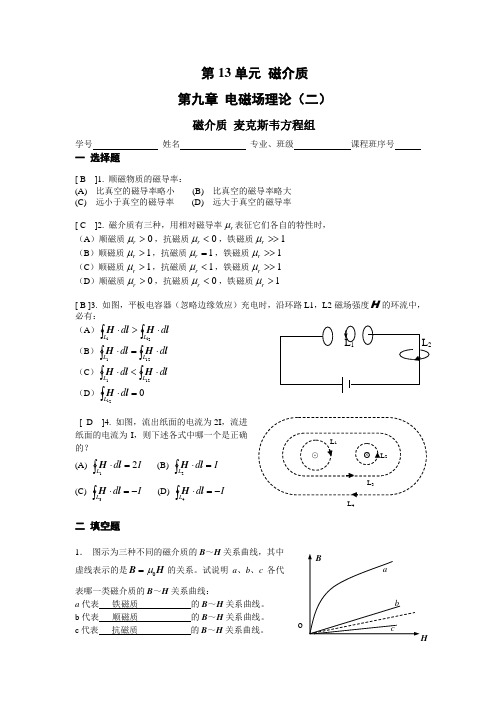
H B a b c o 第13单元 磁介质 第九章 电磁场理论(二)磁介质 麦克斯韦方程组学号 姓名 专业、班级 课程班序号一 选择题[ B ]1. 顺磁物质的磁导率:(A)比真空的磁导率略小 (B)比真空的磁导率略大(C)远小于真空的磁导率 (D)远大于真空的磁导率[ C ]2. 磁介质有三种,用相对磁导率r μ表征它们各自的特性时, (A )顺磁质0>r μ,抗磁质0<r μ,铁磁质1>>r μ(B )顺磁质1>r μ,抗磁质1=r μ,铁磁质1>>r μ(C )顺磁质1>r μ,抗磁质1<r μ,铁磁质1>>r μ(D )顺磁质0>r μ,抗磁质0<r μ,铁磁质1>r μ[ B ]3. 如图,平板电容器(忽略边缘效应)充电时,沿环路L1,L2磁场强度H 的环流中,必有:(A )⎰⎰⋅>⋅211L L d d l H l H(B )⎰⎰⋅=⋅211L L d d l H l H(C )⎰⎰⋅<⋅211L L d d l H l H(D )021=⋅⎰L d l H[ D ]4. 如图,流出纸面的电流为2I ,流进纸面的电流为I ,则下述各式中哪一个是正确的?(A)I d L 21=⋅⎰l H (B) I d L =⋅⎰2l H (C) I d L -=⋅⎰3l H (D) I d L -=⋅⎰4l H二 填空题1. 图示为三种不同的磁介质的B ~H 关系曲线,其中虚线表示的是H B 0μ=的关系。
试说明a 、b 、c 各代表哪一类磁介质的B ~H 关系曲线:a 代表 铁磁质 的B ~H 关系曲线。
b 代表 顺磁质 的B ~H 关系曲线。
c 代表 抗磁质 的B ~H 关系曲线。
L 1 L 2 ⊙ × L 1 L 2 L 3 L 42. 一个单位长度上密绕有n 匝线圈的长直螺线管,每匝线圈中通有强度为I 的电流,管内充满相对磁导率为r μ的磁介质,则管内中部附近磁感强度B = 0r nI μμ,磁场强度H =__nI _。
大学物理第十五章磁介质的磁化习题解答

大学物理第十五章磁介质的磁化习题解答第十五章磁介质的磁化习题解答(仅作为参考)15.1 一均匀磁化的磁介质棒,直径为25mm ,长为75mm ,其总磁矩为12000A·m 2.求棒的磁化强度M 为多少?[解答] 介质棒的面积为S = πr 2,体积为V = Sl = πr 2l ,磁矩为p m = 12000A·m 2,磁化强度为m m p p M V V∑==? 32312000(2510/2)7510π--= =3.26×108(A·m -1).15.3 一螺绕环中心周长l = 10cm ,线圈匝数N = 200匝,线圈中通有电流I = 100mA .求:(1)管内磁感应强度B 0和磁场强度H 0为多少?(2)设管内充满相对磁导率μr = 4200的铁磁质,管内的B 和H 是多少?(3)磁介质内部由传导电流产生的B 0和由磁化电流产生的B`各是多少?[解答](1)管内的磁场强度为302200100101010NI H l --??==? = 200(A·m -1).磁感应强度为B = μ0H 0 = 4π×10-7×200 = 2.5×10-4(T).(2)当管内充满铁磁质之后,磁场强度不变H = H 0 =200(A·m -1).磁感应强度为B = μH = μr μ0H= 4200×4π×10-7×200 = 1.056(T).(3)由传导电流产生的B 0为2.5×10-4T .由于B = B 0 + B`,所以磁化电流产生的磁感应强度为B` = B - B 0 ≈1.056(T).15.5 一根磁棒的矫顽力为H c = 4.0×103A·m -1,把它放在每厘米上绕5匝的线圈的长螺线管中退磁,求导线中至少需通入多大的电流?[解答]螺线管能过电流I 时,产生的磁感应强度为B = μ0nI .根据题意,螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等,但方向相反,因此B = μ0H c ,所以电流强度为I = H c /n = 4.0×103/500 = 8(A).。
高中物理奥林匹克竞赛专题15.磁介质习题(有答案)

高中物理奥林匹克竞赛专题15.磁介质习题(有答案)磁化面电流密度 m A H μB M σs 501076.7⨯=-==磁化面电流 AL σi s s 55101.34.01076.7⨯=⨯⨯== 15-4. 一永磁环的磁化强度为M ,磁环上开有一很窄的细缝。
求图中1、2点处的磁感应强度B 值和磁场强度H 值。
解:H B M 0-=μ由于是一个永磁环 0=•⎰c d l H 所以 02=H15-5. 图a 为铁氧体材料的H B -磁滞曲线,图b 为此材料制成的计算机存贮元件的环形磁芯。
磁芯的内、外半径分别为mm 5.0和mm 8.0,矫顽力为A/m 500π=C H 。
设磁芯的磁化方向如图b 所示,欲使磁芯的磁化方向翻转,试问:(1)轴向电流如何加?至少加至多大时,磁芯中磁化方向开始翻转?(2)若加脉冲电流,则脉冲峰值至少多大时,磁芯中从内而外的磁化方向全部翻转?解:(1)内r i H c π2max=(2)A H r i c 8.0500108.0223max =⨯⨯⨯==-πππ外思考题15-1. 何谓顺磁质、抗磁质和铁磁质,它们的区别是什么?答:顺磁质:磁介质在磁场中磁化后,产生的附加磁场的方向与原来的磁场方向相同。
抗磁质:磁介质在磁场中磁化后,产生的附加磁场的方向与原来的磁场方向相反。
铁磁质:磁介质在磁场中磁化后,产生的附加磁场的方向与原来的磁场方向相同,并且附加磁场远远大于原来磁场。
15-2. 将电介质与磁介质加以比较.答:略15-3. 何谓磁滞回线?答:对于铁磁质来说,磁感应强度B 随磁场强度H 的变化而变化所形成的闭合曲线就叫磁滞回线。
见教材P107页图15-11。
15-4. 在两个分界面,磁感应强度和磁场强度的关系如何?答:在两个分界面磁场强度的法向分量是连续的,磁感应强度的法向分量不连续。
磁介质测试题及答案

磁介质测试题及答案一、选择题1. 磁介质的磁性能主要取决于以下哪一项?A. 材料的化学成分B. 材料的微观结构C. 材料的制备工艺D. 外部磁场强度答案:B2. 以下哪种类型的磁介质具有最高的磁导率?A. 软磁材料B. 硬磁材料C. 铁磁材料D. 反铁磁材料答案:A3. 磁介质的磁滞回线反映了材料的哪些特性?A. 磁导率B. 磁饱和度C. 磁滞损失D. 所有上述选项答案:D二、填空题4. 磁介质的_______是指材料在没有外磁场作用时,内部磁畴的排列状态。
答案:初始磁化状态5. 磁介质的_______是指材料在外加磁场作用下,磁化强度达到最大值的能力。
答案:磁饱和度三、简答题6. 简述磁介质在存储设备中的应用及其重要性。
答案:磁介质在存储设备中主要用于数据的存储。
由于磁介质具有较高的磁导率和磁饱和度,它们能够存储大量的数据信息。
此外,磁介质的稳定性和可重复写入特性使其在硬盘驱动器、磁带和其他存储设备中得到广泛应用。
磁介质的性能直接影响存储设备的容量、速度和可靠性。
7. 描述磁介质的磁滞回线,并解释其物理意义。
答案:磁滞回线是描述磁介质在外加磁场作用下磁化强度与磁场强度之间关系的曲线。
当外加磁场逐渐增大时,磁介质的磁化强度随之增加,但存在一定的滞后现象。
当磁场减小到零时,磁介质的磁化强度不会立即回到零,而是存在一个剩余磁化强度。
这个剩余磁化强度与外加磁场的相互作用导致了磁滞损失,这是磁介质在反复磁化过程中能量损耗的来源。
磁滞回线的形状和位置反映了磁介质的磁性能,如磁导率、磁饱和度和磁滞损失等。
四、计算题8. 假设有一磁介质样品,其磁化强度M随外加磁场H的变化关系为M = 0.5H。
如果外加磁场从0增加到2000 A/m,计算磁介质样品的磁化强度变化范围。
答案:根据给定的关系M = 0.5H,当外加磁场H从0增加到2000 A/m时,磁化强度M的变化范围是从0增加到1000 A/m(即0.5 * 2000 A/m)。
磁介质一章习题答案

磁介质一章习题答案习题10—1 将一有限长圆柱形的均匀抗磁质放在一无限长直螺线管内,其螺线管线圈的电流方向如图所示。
在a 、b 、c 三点的磁感应强度与未放入抗磁质前相比较其增减情况是:[ ](A) a 点增加,b 点减小,c 点不变。
(B) a 点增加,b 点增加,c 点增加。
(C) a 点减小,b 点减小,c 点增加。
(D) a 点减小,b 点增加,c 点减小。
解:抗磁质放在一无限长直螺线管内,相当于把它放在均匀的外磁场中。
现 已知外场0B 方向向右。
对磁介质中的a 点来说,其本身磁化电流产生的附加磁场B '的方向与外场方向相反,叠加的结果使a 点的场减小;对介质外的b 点来说,外场0B 方向仍旧向右,这时的抗磁质相当于N 极在左、S 极在右的磁铁,其附加磁场B '的方向在b 点向左,因此,b 点的场也减小;对介质外侧的c 点来说,外场0B 方向仍旧向右,但是在该处B '的方向也向右,与外场同向,故c 点的场是增加的。
综上所述,应该选择答案(C)。
习题10—2 图示三种不同磁介质的磁化曲线,虚线表示真空中的B —H 关系。
则表示铁磁质的是曲线 ;表示抗磁质的是曲线 ;表示顺磁质的是曲线 。
解:真空中的B —H 关系为:H B 0μ=;对一般弱磁介质的B —H 关系为:H H B r μμμ0==,式中r μ为常数,若为顺磁质,则1>r μ因而0μμ>;若为抗磁质,则1<r μ因而0μμ<,所以若以真空中的B —H关系曲线为参考,则曲线Ⅱ表示的是顺磁质,曲线Ⅲ表示的是抗磁质。
对于铁磁质其B —H关系仍然为:H H B r μμμ0==,但是,由于其r μ不是常数,即)(H r r μμ=,因此其B —H 关系是非线性的,相应的B —H 关系曲线亦非直线,故而表示铁磁质的应是曲线Ⅰ。
习题10—3 关于稳恒磁场的磁场强度H 的下列几种说法中哪一个是正确的? (A) H 仅与传导电流有关。
大物习题解答-大学物理习题答案(许瑞珍_贾谊明)-第8章 磁场中的磁介质

第八章 磁场中的磁介质8-1一螺绕环的平均半径为R=0.08m ,其上绕有N=240匝线圈,电流强度为I=0.30A 时管内充满的铁磁质的相对磁导率μr =5000,问管内的磁场强度和磁感应强度各为多少? 解:(1)由I d =⋅⎰l H L 得I R N H NI R H π=→=π22代入数值为 m A H /1043.108.014.323.02402⨯=⨯⨯⨯= (2)T H B r 9.01043.150********=⨯⨯⨯⨯π=μμ=-8-2在图11-8所示的实验中,环型螺绕环共包含500匝线圈,平均周长为50cm ,当线圈中的电流强度为2.0A 时,用冲击电流计测得介质内的磁感应强度为2.0T ,求这时(1)待测材料的相对磁导率μr ;(2)磁化电流线密度j s 。
解:(1)I R N H π=2代入数值m A H /2000105025002=⨯⨯=- 7962000104270=⨯⨯π=μ=μ-H B r (2)m A nI j r s /1056.121050500)1796()1(62⨯=⨯⨯⨯-=-μ=- 8-3如图所示,一根长圆柱型同轴电缆,内、外导体间充满磁介质,磁介质的相对磁导率为μr (μr <1),导体的磁化可以略去不计,电缆沿轴向有稳定电流I 通过,内外导体上的电流的方向相反,求(1)空间各区域的磁感应强度和磁化强度;(2)磁介质表面的磁化电流。
解:依题意,内圆柱的电流密度21R I j π=(1)r<R 时: 根据∑⎰=⋅I d l H L得21121222R Ir jr H r j r H π==→π=π 2101012R Ir H B πμ=μ= 0)1(11=-μ=H M r (导体的μr =1)R 1<r<R 2时:根据∑⎰=⋅I d l H L 得rI H I r H π=→=π2222 r I H B r r πμμ=μμ=20202习题8-3图r I H M r r π-μ=-μ=2)1()1(22 R 2<r<R 3时: )(2223R R I j -π= 根据∑⎰=⋅I d l H L 得222322332223)(2)(2R R r R r I H R r j I r H --π=→-π-=π 22232230303)(2R R r R r I H B --πμ=μ= 0)1(33=-μ=H M r (导体的μr =1)r>R 3时:H=0, B=0, M=0(2)I I r s )1(-μ=8-4一个截面为正方形的环形铁心,其中磁介质的相对磁导率为μr ,若在此环形铁心上绕有N 匝线圈,线圈中的电流为I ,设环的平均半径为r ,求此铁心的磁化强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁介质习题
1、螺线环中心周长l=10cm ,环上均匀密绕线圈N=200匝,线圈中通有电流I=100mA 。
(1)求螺线管内的磁感应强度B 0和磁场强度H 0 ;(2)若管内充满相对磁导率为μr=4200的磁性物质,则管内的B 和H 是多少?
分析:螺线环内的磁感应强度具有同心圆的轴对称分布,对均匀密绕的细螺绕环可认为环内的磁感应强度均匀;环外的磁感应强度为零。
磁场强度H 的环流仅与传导电流有关,形式上与磁介质的磁化无关。
解:(1)管内为真空时,由安培环路定理,
∑⎰=⋅i
i L I d l H
0 m A I l
N nI H /2000=== 磁感应强度为T H B 40001051.2-⨯==μ
(2)管内充满磁介质时,仍由安培环路定理可得
m A I l
N nI H /200=== 磁感应强度为T H H B r 06.10===μμμ
2、一磁导率为μ1的无限长圆柱形直导线,半径为R 1,其中均匀地通有电流I ,在导线外包一层磁导率为μ2的圆柱形不导电的磁介质,其外半径为R 2。
试求磁场强度和磁感应强度的分布。
分析:系统具有轴对称性分布,因此,空间的磁场分布也应具有轴对称性。
利用安培环路定理可求出空间磁感应强度和磁场强度的分布。
解:以轴到场点的距离为半径,过场点作环面垂直于轴的环路,取环路的方向与电流方向成右手螺旋关系,应用安培环路定理。
当r<R 1时,环路包含的传导电流为
221
1r R I I ππ= 由安培环路定理1I d =⋅⎰l H ,得
2112R Ir H π= 21
11112R Ir H B πμμ== 当R 1<r<R 2时,环路包含的传导电流为I I =2, 由安培环路定理2I d =⋅⎰
l H ,得 r I
H π22= r
I H B πμμ22222=
=
当r>R 2时,环路包含的传导电流为I I =3, 由安培环路定理3I d =⋅⎰
l H ,得 r I
H π23= r
I H B πμμ20303== 3、一根长直导线,其μ≈μ0 ,载有电流I ,已知电流均匀分布在导线的横截面上。
试证明:单位长度导线内所储存的磁能为π
μ162
0I 。
分析:空间具有轴对称性,可由安培定理求出空间的磁感应强度分布,再求出磁能密度,由磁能密度对空间的积分,求出磁场的能量。
证明:设无限长直载流导线为圆柱形导体,半径为R ,由安培环路定理得
⎪⎪⎩⎪⎪⎨⎧=I r
I R r B πμπμ22020 )()(R r R r ><
导线内的磁能密度:
422202200028)2(212R
r I I R r B w m πμπμμμ=== 在导线内长为L 的同轴薄圆柱筒体积元dV = 2πrLdr ,其磁能为
dr r R
L I dV w dW m m 34204πμ== 长为L 的导体的磁能为
L I dr r R L I dW W R m m πμπμ1642
030
420===⎰⎰ 单位长导线内的磁能:
π
μ162
0I L W W m m ==' 4、一个直径为0.01m ,长为0.10m 的长直密绕螺线管,共1000匝线圈,总电阻为7.76Ω。
如果把线圈接到电动势ε=2.0V 的电池上,电流稳定后,线圈中所储存的磁能有多少?磁能密度是多少?
分析:本题可由线圈的自感系数求得磁能的磁能密度。
解:长直密绕螺线管的自感系数为
l S
N L 20μ=
电流稳定后有R I ε
=,则线圈储存的磁能为
J lR
S N LI W m 522
2021028.3221-⨯===εμ 在忽略端部效应时,可认为磁场全部并均匀分布于螺线管的内部,所以磁能密度为 3/17.4m J SL
W w m m ==。
