2.3 功和动能定理
大学物理-动能定理

4. 势能曲线
Ep (h)
E
Eh
Ep
o
H H h
重力势能
Ep
E
o
Ek
Ep
3-4 动能定理
Ep (x)
AE
B
Ek
Ep
o
x
弹性势能
Ek 0
x
引力势能
26
势能曲线的作用:
3-4 动能定理
(1)根据势能曲线的形状可以讨论物体的运动。
(2)利用势能曲线,可以判断物体在各个位置 所受保守力的大小和方向。
力提供园周运动的向心力而不做功,摩擦力做负
功使滑块动能减少。
W
1 mv2 2
1 2
mv0
2
(1)
34
3-4 动能定理
v2 N m
(2)
R
N m dv
(3)
dt
将式(2)代入式(3),整理变形为
v2 dv dv d v dv R dt dt d R d
分离变量并积分,得
做功,它们所做元功之和为
dA fij dri f ji drj
因
fij f ji
mi
drji
dri
rij
rij drij
所以
fij
dA fij (dri drj ) fij drij
f ji m j drj
讨论:内力做功的特点
14
成对力的功
对它所作的功为零.
非保守力:力所作的功与路径有关. (例如摩擦力)
23
3. 势能
3-4 动能定理
2-3 功 动能 动能定理

b
F
Aab =
=
=
∫
∫
b a
b
F idr =
∫
∫
Ft d s
dv ds m dt
F a n
a
m at d s =
∫
vb va
定义质点的动能为: E = 1 m v 2 k
1 1 2 2 m v d v = m vb − m va 2 2
Aab = E kb − E ka = ΔE k
8/20 中国矿业大学(北京)
F
300
11/20
中国矿业大学(北京)
例题2-9
解: 木箱所受的力为: 拉力F ,重力G , 斜面对木箱的支持力N , 斜面对木箱的摩擦力fr 。
N
F 100
fr G
300
(1)拉力F 所做的功A1 , (已知l=3m) 重力 G 所做的功A2 :
d A = F ⋅dr
3
A1 = Fl cos 10 = 700 × 3 × 0.985J = 2.07 × 10 J
第2段近似功:
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 第i 段近似功:
总功近似为:
ΔA2 = F2 ⋅ Δr2
Δr3 Δr2
Δr1
a
Δr4
Δri
F4
F2
F3
Fi b
⋅⋅⋅⋅⋅⋅
Δ Ai = Fi iΔri
F1
Aab = ∑ Δ Ai = ∑ Fi iΔri
i i
6/20 中国矿业大学(北京)
动能定理
当 Δri → 0 时,可以得到变力做的总功的精 确值Aab。
18/20 中国矿业大学(北京)
例题2-11
N(随x变化) L O L N
2-3功动能定理

Wx
xB
xA
Fx d x
Wy
yB
yA
Fy dy
Wz
zB
zA
Fz d z
W Wx W y Wz
功的单位(焦耳) 平均功率 P
W t
1J 1 N m
瞬时功率 P
dW dt
F dr dt
F v
(瓦特) 功率的单位 3 1 1 kW 10 W 1 W 1 J s
能量
能量是反映各种运动形式共性的物理量,是各
种运动形式的一般量度.
到十九世纪,能量概念才逐步由力的概念中分 离出来.实际上,只有在能量的转换和守恒定律发 现以后,人们才认识功、动能和势能的真实含义. 二十世纪初,爱因斯坦建立了狭义相对论,得到了 “质能关系”,进一步揭示能量和质量的相当性, 对于能量的认识才更深入了一步.
v0
v
m1
m2
解
(1) 把木块与车选为一个系统, 水平方向无外 力作用, 所以动量守恒.
m 2 v 0 ( m 2 m1 ) v
考虑中间的某个状态, 物块和小车的速度不相同, 这时也有动量动量守恒关系:
m 2 v 0 m 2 v 木 m1 v 车
(2)木块与小车之间没有相对位移,一对摩擦内力作功. 木块所受摩擦力: mg ;方向与运动方向相反 木块对地的位移: l d 木块所受摩擦力作功: mg ( l d ) 小车受的摩擦力: mg ;方向与运动方向相同 小车对地的位移: l 小车所受摩擦力作功: mgl 一对内力作功的代数和为
质点系动能定理 W 注意
ex
W
i
in
高中物理鲁科版总结公式归纳知识体系详细概括

高中物理鲁科版总结公式归纳知识体系详细概括高中物理是理工类学生必修的一门科目,它的学习涉及到许多基本概念、定律和公式。
这些公式是解决物理问题的重要工具,它们能够帮助我们理解物质世界的运行规律。
在鲁科版的高中物理教材中,我们可以找到许多重要且常用的公式,下面将对这些公式进行详细归纳和总结。
1. 运动学1.1 直线运动1.1.1 速度公式:v = Δx / Δt1.1.2 加速度公式:a = Δv / Δt1.1.3 位移公式1:Δx = (v + u) * t / 21.1.4 位移公式2:Δx = ut + 1/2at^21.1.5 速度-时间关系式:v = u + at1.2 抛体运动1.2.1 抛体运动位移:h = ut + 1/2gt^21.2.2 抛体运动的水平速度:v = u + gt1.2.3 抛体运动的最大高度:h_max = u^2 / (2g)1.2.4 抛体运动的总时间:T = 2u / g1.2.5 抛体运动的最大水平位移:R = v * T = u^2 / g1.3 圆周运动1.3.1 圆周运动的周期:T = 2πr / v1.3.2 圆周运动的频率:f = 1 / T1.3.3 圆周运动的向心加速度:a_c = v^2 / r2. 力学2.1 牛顿定律2.1.1 牛顿第一定律(惯性定律):物体在受力作用下保持匀速直线运动或静止状态2.1.2 牛顿第二定律:F = ma,力等于物体质量乘以加速度2.1.3 牛顿第三定律:作用力与反作用力大小相等、方向相反、作用在不同物体上2.2 动力学2.2.1 动量公式:p = mv,动量等于物体质量乘以速度2.2.2 冲量公式:J = FΔt,冲量等于物体受到的力与时间的乘积2.2.3 作用-反作用定理:作用在两个物体之间的相互作用力大小相等、方向相反2.3 动能定理2.3.1 动能公式:E_k = 1/2mv^2,动能等于物体质量乘以速度的平方的一半2.3.2 动能定理:E_k = W,物体所受合外力所做的功等于物体的动能变化量2.3.3 功率公式:P = W / Δt,功率等于所做的功除以时间的变化量3. 热学3.1 热力学第一定律:Q = ΔU + W,热量等于内能变化量与对外做功的和3.2 热力学第二定律:热量不会自发地从低温物体传递给高温物体3.3 理想气体定律:PV = nRT,气体的压强乘以体积等于物质的摩尔数乘以气体的通用气体常数乘以温度4. 光学4.1 光的直线传播定律:光在任意介质中沿直线传播4.2 光的反射定律:入射角等于反射角4.3 光的折射定律:折射角的正弦与入射角的正弦的比例等于两种介质的折射率之比4.4 光的衍射定律:波通过一个够小的孔洞或者通过一个够窄的缝隙时产生衍射现象4.5 牛顿环公式:r^2 = (2nt)λ,牛顿环的半径与介质折射率、透明物体的厚度、波长之间的关系以上是高中物理鲁科版中一些主要的公式的总结和归纳,这些公式是解决物理问题的重要工具,掌握好这些公式并且能够熟练运用,将有助于提高解决物理问题的能力和水平。
高考物理动能定理及其应用考点总结

如图5-2-3所示,一质量为m=1 kg的物块静止 在粗糙水平面上的A点,从t=0时刻开始,物块受到按如 图5-2-4所示规律变化的水平力F作用并向右运动,第3 s 末物块运动到B点时速度刚好为0,第5 s末物块刚好回到A 点,已知物块与粗糙水平面之间的动摩擦因数μ=0.2,求 (g取10 m/s2):
在牵引力不变的条件下行驶45 m
的坡路到达B点时,司机立即关
图5-2-9
掉油门,以后汽车又向前滑行15 m停在C点,汽车的
质量为5×103 kg,行驶中受到的摩擦阻力是车重的
0.25倍,取g=10 m/s2,求汽车的牵引力做的功和它
经过B点时的速率.
解析:汽车从A到C的过程中,汽车的发动机牵引力做正 功,重力做负功,摩擦力做负功,动能的变化量为零, 由动能定理可得WF-WG-W阻=0,由于G、F阻已知, 汽车的位移也知道,所以有 WF=WG+W阻=mgh+0.25mgl=2.25×106 J.
2.如图5-2-1所示,ABCD是一个盆式容器,盆内 侧
壁与盆底BC的连接处都是一段与BC相切的圆弧, BC是水平的,其长度d=0.50 m.盆边缘的高度为 h=0.30 m.在A处放一个质量为m的小物块并让其 从静止下滑.已知盆内侧壁是光滑的,而盆底BC 面与小物块间的动摩擦因数为μ=0.10.小物块在盆 内来回滑动,最后停下来,则停的地点到B的距离 为( )
1.质量为m的物体在水平力F的作用下由静止开始在光滑
地面上运动,前进一段距离之后速度大小为v,再前进一
段距离使物体的速度增大为2v,则
()
A.第二过程的速度增量等于第一过程的速度增量
B.第二过程的动能增量是第一过程的动能增量的3倍
C.第二过程合外力做的功等于第一过程合外力做的功
大学物理2-3功 动能 动能定理
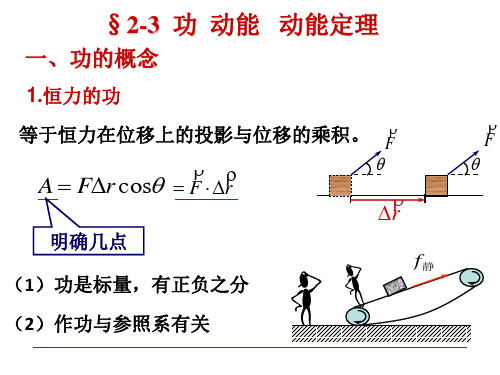
一、功的概念
1.恒力的功
等于恒力在位移上的投影与位移的乘积。 F
F
A Fr cos F r
明确几点
r
f静
(1)功是标量,有正负之分
(2)作功与参照系有关
2.变力的功
物体在变力的作 用下从a运动到b。
a
怎样计算这个力 的功呢? 采用微元分割法
当物体前端在s处停止时,摩擦力做的功为 L m s A F d x f r d x gx d x mg d x 0 L L L L mg ( s L) mg ( s )
2 2
再由动能定理得
即得
L 1 2 mg ( s ) 0 mv0 2 2 L v0 2 g ( s ) 2
2
l G x
所得结果相同,而现在 的解法无疑大为简便。
x
B
例题2-11 传送机通过滑道将长为L,质量为m的柔软 匀质物体以初速v0向右送上水平台面,物体前端在台 面上滑动 S距离后停下来(如图)。已知滑道上的磨 擦可不计,物与台面间的摩擦系数为 μ ,而且 S>L , 试计算物体的初速度v0。
动能定理:合外力对质点所做的功等于质点动 能的增量。
Aab Ekb Eka Ek
几点注意: a. 合力做正功时,质点动能增大;反之,质 点动能减小。 b.动能的量值与参考系有关。
c.动能定理只适用于惯性系。
d. 功是一个过程量,而动能是一个状态量, 它们之间仅仅是一个等量关系。
例题2-9 装有货物的木箱,重G=980N,要把它运 上汽车。现将长 l = 3m 的木板搁在汽车后部,构成一斜 面,然后把木箱沿斜面拉上汽车。斜面与地面成30o角, 木 箱 与 斜 面 间 的 滑 动 摩 擦 系 数 =0.20 , 绳 的 拉 力 与斜面成10o角,大小为700N,如图所示。
§2-3 功 动能 动能定理
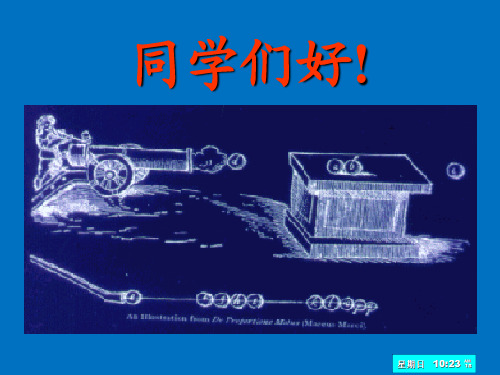
r1
A始末
末 始
f2
d r21
表明:任何一对作用 力和反作用力所作的总功
B1
B2 f2
f1
d
r1
r1
m1
r2
d r2
m2
A2
具有与参考系选择无关的 不变性质。
O
A1
一对力所作的总功的只取决于两质点的相对运动;
一对力做功的代数和与参考系的选择无关;
什么条件下一对内力做功为零?
v
C
m M f
Fi
直角坐标系:
F
Fxi
Fy
j
Fz
k
dr dxi dyj dzk
元功:
dA
F
dr
Fxdx
Fy
dy
Fzdz
总功:
A
b
dA
b
F
cosds
b
F
dr
a
a
a
b
Fxdx Fydy Fzdz
2.合力的功
a
F cos
Aab
b
F
dr
a
b
Fi
dri
r o rA dr rB
a
b
Fi
f12
f21
m2
作为系统考虑时,得到:
b1 a1
F1
dr1
b2 a2
F2
dr2
b1 a1
f12
dr1
b1 a1
f21 dr2
(1 2
m1v12b
1 2
m2v22b )
(1 2
m1v12a
1 2
m2v22a
)
A外 A内 Ekb Eka Ek
功,功率,动能定理知识点总结

功,功率,动能定理知识点总结一、功。
1. 定义。
- 一个物体受到力的作用,并在力的方向上发生了一段位移,这个力就对物体做了功。
- 公式:W = Fxcosθ,其中W表示功,F是力的大小,x是位移的大小,θ是力与位移方向的夹角。
2. 功的正负。
- 当0≤slantθ <(π)/(2)时,cosθ> 0,力对物体做正功,力是动力,物体的能量增加。
- 当θ=(π)/(2)时,cosθ = 0,力对物体不做功,例如物体做圆周运动时向心力不做功。
- 当(π)/(2)<θ≤slantπ时,cosθ<0,力对物体做负功,力是阻力,物体的能量减少。
3. 合力的功。
- 方法一:先求出物体所受的合力F_合,再根据W = F_合xcosθ计算合力的功,这里的θ是合力与位移方向的夹角。
- 方法二:分别求出各个力做的功W_1,W_2,W_3,·s,然后根据W_合=W_1 + W_2+W_3+·s计算合力的功。
二、功率。
1. 定义。
- 功率是描述力对物体做功快慢的物理量。
- 公式:P=(W)/(t),其中P表示功率,W是功,t是完成这些功所用的时间。
2. 平均功率和瞬时功率。
- 平均功率:P=(W)/(t),也可以根据P = F¯vcosθ计算,其中¯v是平均速度。
- 瞬时功率:P = Fvcosθ,其中v是瞬时速度。
当F与v同向时,P = Fv。
3. 额定功率和实际功率。
- 额定功率:是发动机正常工作时的最大功率,通常在发动机铭牌上标明。
- 实际功率:是发动机实际工作时的功率,实际功率可以小于或等于额定功率,不能长时间大于额定功率。
三、动能定理。
1. 动能。
- 定义:物体由于运动而具有的能量叫动能,表达式为E_k=(1)/(2)mv^2,其中m是物体的质量,v是物体的速度。
- 动能是标量,且恒为正。
2. 动能定理。
- 内容:合外力对物体做的功等于物体动能的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 单 位
F • dr = dt = dt dr F• = • v = dt F =Fvcosθ
dA
瓦 特 (W) )
-1
1 J• s = 1W •
2.3 功和动能定理
第2章 质点动力学
17
v0 6.一对 m
内 的 力 功
f车对木块 f木块对车
v
d
(1)车为参照系 A摩擦力对 (1)车为参照系 摩擦力对m
4
二、冲量 1.恒力的冲量 1.恒力的冲量
恒力F 变力
∆t dt
t1 F 恒力 t2
I
= F∆t
大小
I = F∆t
方向一致 方向 与 F 2.变力的冲量 2.变力的冲量 (1)任取时间元 (1)任取时间元dt 任取时间元
作者 杨 鑫
( 2 ) 计算 元冲量
dI = Fdt
t2
(3)计算总冲量 (3)计算总冲量
a
•
作者 杨 鑫
= Fdrcosθ θ F b (3)计算总功 dr (3)计算总功
b
dA= F • dr
第2章 质点动力学
13
例题2.3-1 例题2.3- 2.3
2.3 功和动能定理
第2章 质点动力学
14
3. 直 角 坐 标 系 中 的 功
作者 杨 鑫
A = ∫ F • dr
• ( x i +F y j ) (dxi +dy j) F =∫
2.3 功和动能定理
第2章 质点动力学
11
2.3 功和动能定理 一、功 二、质点的动能定理 三、质点系的动能定理
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
12
一、功 1.恒力的功 1.恒力的功
功 是 标 量,但 有 正 负 之 分
F 恒力 F
θ
A=F•r = F r cosθ
作者 杨 鑫
t2
1
I z = ∫t Fz dt= mv2z− mv1z =Fz∆t
t2
1
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
8
(2)矢量图示法 (2)矢量图示法
I = F∆t = ∆ mv
冲 量 大 小
mv 2
1
∆mv= I
冲 量 增 量 方 的 向 方 向 动 量
Δ = mv2 − mv1 mv = FΔt
第2章 质点动力学
18
v0 m
f车对木块 f木块对车
v
(5)车为参照系 (5)车为参照系 A一对摩擦力 (6)地为参照系 (6)地为参照系 A一对摩擦力
d
l
一对 与参考系无关 内力 与两物体间的 的功 相对位移有关
= −µmgd
= −µmgd
一对 其中一个物体所受的力 内力 等 于 沿着该物体相对另一物体 的功 所移动的路径所作的功
| I | =| F |∆t=| ∆mv |
F=
|I|
= ∆t
| ∆mv |
作者 杨 鑫
∆t
2.3 功和动能定理
第2章 质点动力学
9
五、动量守恒定律 (3) 分量式 1. ∑Fi 0 ∑Fix = 0 ∑ Pix 恒量 内 恒量 容 ∑P i ∑ Fiy = 0 ∑ Piy 恒量 2.注意几点 2.注意几点 内力 ∑ Fiz = 0 ∑ P 恒量 iz F 外 (1) 满足守恒条件 各质点的动量对应 (4) 同一惯性参考系 ∑mi vi 不变 (2) 是自然界中最普遍 不是说每个质 (5) 点动量都不变 最基本定律之一
一切外力与一切内力所作功的 一切外力与一切内力所作功的代数和 外力与一切内力所作功的代数和 等 于 质 点 系 动 能 的 增 量
作者 杨 鑫
= Ek 2 − Ek1
例题2.3- 例题2.3-2 2.3
例题2.3- 例题2.3-3 2.3
2.3 功和动能定理
第2章 质点动力学
23
一、功 1.恒力的功 1.恒力的功
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
19
二、质点的动能定理
dA =F • dr
dr θ
Ft
b v2
=Fdr cosθ =Ft d r =m at dr
作者 杨 鑫
m F
a v1 dr = ds
பைடு நூலகம்
dv dr =m dt =m v dv
2.3 功和动能定理
第2章 质点动力学
20
A = ∫ dA
I = ∫ dI = ∫ Fdt
t1
2.3 功和动能定理
第2章 质点动力学
5
3.用分量式求冲量步骤 3.用分量式求冲量步骤 (1)建 坐 标 (1)建 (2)求冲量 分 量 (3)求合冲量 (3)求合冲量
I x = ∫t Fx dt =Fx ∆t
t2
1
I y =∫t Fy dt = Fy ∆t
t2
2.变力的功 2.变力的功 (1)任取位 (1)任取位 移元 d 恒力 r F F (2)计算元功 (2)计算元功
b
dr
b
θ
F
内容小结
作者 杨 鑫
r =Frcosθ
A = F•
r
• dr a dA= F
(3) 计 算 总 功
θ
A =∫a F • dr
=∫a F drcosθ
b
2.3 功和动能定理
3.直角坐标系中的功 3.直角坐标系中的功 4.合力 的 功 5.一对 内 力 的 功 6.功 6.功
b
F1 • dr + ∫aF2 • dr =∫a
b b
作者 杨 鑫
+ ⋯ ∫a Fn • dr + = A + A + ⋯+ An 1 2
b
2.3 功和动能定理
第2章 质点动力学
16
5.功 5.功
率
(1)平均功率 (1)平均功率
P
=∆t
∆A
(2)瞬时功率 (2)瞬时功率
∆A l m P=∆ ti→0 ∆t
1
I = Ix i + I y j
4.单位 4.单位
作者 杨 鑫
大 小
I = I +I
2 x
2 y
N• s •
方 tan(I , i )= I y 向
Ix
2.3 功和动能定理
第2章 质点动力学
6
三、质点与质点系的动量定理 1. 质
t2 ∫t1 F dt
t2 ∑Fi dt ∫t1
=mv2−mv1
点 质点所受合外力的冲量 表 等 于 质 点 动 量 的 增 量 达 质 点 质点系所受 合外力的冲量 等于 式 质点系所受合外力的冲量 合外力的冲量等于 系 质 点 系 总 动 量 的 增 量
2.3 功和动能定理
第2章 质点动力学
1
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
2
一、动 量 1.质点动量 1.质点动量
t 时 刻 大小 方向
P
= mv
2.质点系动量 2.质点系动量
内 m 容 P = mv 回 与 v 方向一致 顾
vn m1 v m 2 n
2
v1
= m1v1+ m2v2+ ⋯+ mnvn ∑ mi vi P= i =1
= =
<<
= = =
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
10
六、碰撞
v10
m1
(1)弹 (1)弹 性
v20
m2
碰
v1
v2
f12
撞 动
f21
动能守恒 动能不守恒
(2)非 (2)非 弹 性 碰 撞 量
守 动能不守恒 (3)完全非弹性碰撞 (3)完全非弹性碰撞 恒 碰后有共同速度
作者 杨 鑫
a r
b
θ =π 2 A= 0 π 2< θ ≤π A< 0
单
0 ≤ θ < π 2 A> 0
(J )
(eV)
位 1eV =1.6×10-19J ×
2.3 功和动能定理
2.变力的功 2.变力的功
A=∫aF dr (1)任取位移元 r (1)任取位移元d b =∫ aFdrcosθ (2)计算元功 (2)计算元功
作者 杨 鑫
=
∑ mi vi ∑ mi vi 0
−
2.3 功和动能定理
第2章 质点动力学
7
2.计算质点合外力冲量(动量增量)的方法 2.计算质点合外力冲量(动量增量) 计算质点合外力冲量 (1)解析法 (1)解析法
I x = ∫t Fx dt= mv2x− mv1x =Fx∆t
t2
1
I y =∫t Fy dt= mv2 y− mv1y =Fy∆t
作者 杨 鑫
A = Ax+ Ay A = A + A + ⋯+ An 1 2
其中一个物体所受的力 等 沿着该物体相对另一物体 于 所移动的路径所作的功
第2章 质点动力学
24
合力的功等于各分力功的代数和
率
P =F • v = vcosθ F
2.3 功和动能定理
第2章 质点动力学
25
二、质点的动能定理
作者 杨 鑫
t1时 刻
v1
l2
v2
2.3 功和动能定理
第2章 质点动力学
22
(∫l F1 • dr + ∫l F2 • dr )
1 2
+ (∫l f12 • dr +∫l f21 • dr )
