等腰三角形典型例题练习(含答案)
等腰三角形练习题(含答案)

等腰三角形练习题(含答案)等腰三角形第1课时:等腰三角形的性质1.已知等腰三角形的一个底角为50°,则其顶角为80°。
2.如图,△ABC中,AB=AC,BC=6cm,AD平分∠BAC,则BD=3cm。
3.如图,△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为45°。
4.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为80°。
5.如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,求∠C的度数为100°。
6.如图,△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC上的点,且AE=AF。
证明:DE=DF。
第2课时:等腰三角形的判定1.在△ABC中,∠A=40°,∠B=70°,则△ABC为钝角三角形。
2.已知△ABC中,∠B=50°,∠A=80°,AB=5cm,则AC=5cm。
3.如图,在△ABC中,AD⊥BC于点D,且BD=DC,则△ABC为等腰三角形。
4.如图,已知△ABC中,∠A=36°,AB=AC,BD为∠ABC的平分线,则图中共有2个等腰三角形。
5.如图,D是△XXX的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E,F,且DE=DF。
证明:AB=AC。
6.如图,AB∥CD,直线l交AB于点E,交CD于点F,FG平分∠EFD交直线AB于点G。
证明:△EFG是等腰三角形。
等边三角形第1课时:等边三角形的性质与判定1.如图,a∥b,等边△ABC的顶点B,C在直线b上,则∠1的度数为60°。
2.在△ABC中,∠A=60°,现有下面三个条件:①AB=AC;②∠B=∠C;③∠A=∠B。
能判定△ABC为等边三角形的有条件①、②、③。
3.如图,在等边△ABC中,BD⊥AC于D,若AB=4,则AD=2.4.如图,△ABC是等边三角形,∠CBD=90°,BD=BC,连接AD交BC于点E,求∠BAD的度数为75°。
等腰三角形的性质练习(含答案)

等腰三角形的性质一、基础能力平台1.选择题:(1)等腰三角形的底角与相邻外角的关系是()A.底角大于相邻外角B.底角小于相邻外角C.底角大于或等于相邻外角D.底角小于或等于相邻外角(2)等腰三角形的一个内角等于100°,则另两个内角的度数分别为()A.40°,40°B.100°,20°C.50°,50°D.40°,40°或100°,20°(3)等腰三角形中的一个外角等于100°,则这个三角形的三个内角分别为()A.50°,50°,80°B.80°,80°,20°C.100°,100°,20°D.50°,50°,80°或80°,80°,20°(4)如果一个等腰三角形的一个底角比顶角大15°,那么顶角为()A.45°B.40°C.55°D.50°(5)等腰三角形一腰上的高与底边所成的角等于()A.顶角B.顶角的一半C.顶角的2倍D.底角的一半(6)已知:如图1所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A 的度数为()A.30°B.45°C.36°D.72°(1)(2)(3)2.填空题:(1)如图2所示,在△ABC中,①因为AB=AC,所以∠________=∠______;②因为AB=AC,∠1=∠2,所以BD=_____,_____⊥______.(2)若等腰三角形的顶角与一个底角之和为110°,则顶角的度数为______.(3)已知等腰三角形的一个角是80°,则顶角为______.(4)在等腰三角形ABC中,一腰上的高是1cm,这条高与底边的夹角是450,则△ABC 的面积为________.(5)如图3所示,O为△ABC内一点,且OA=OB=OC,∠ABO=20°,∠BCO=30°,则∠CAO=______.3.等腰三角形两个内角的度数比为4:1,求其各个角的度数.4.如图,已知线段a和c,用圆规和直尺作等腰三角形ABC,使等腰三角形△ABC•以a和c为两边,这样的三角形能作几个?ac5.如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠BAC的度数.6.如图所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点.(1)AF与CD垂直吗?请说明理由;(2)在你接连BE后,还能得出什么新的结论?请写出三个.(不要求说明理由)7.如图,在△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE.AH与2BD•相等吗?请说明理由.二、拓展延伸训练右下图是人字型层架的设计图,由AB、AC、BC、AD四根钢条焊接而成,其中A、B、C、D均为焊接点,且AB=AC,D为BC的中点,现在焊接所需的四根钢条已截好,且已标出BC的中点D.如果焊接工身边只有可检验直角的角尺,那么为了准确快速地焊接,他首先应取的两根钢条及焊接的点是()A.AC和BC,焊接点B B.AB和AC,焊接点AC.AD和BC,焊接点D D.AB和AD,焊接点A三、自主探究提高如图,在△ABC中,CD是边AB上的中线,且DA=DB=DC.(1)已知∠A=30°,求∠ACB的度数;(2)已知∠A=40°,求∠ACB的度数;(3)试改变∠A的度数,计算∠ACB的度数,你有什么发现吗?答案:【基础能力平台】1.(1)B(2)A(3)D(4)D(5)B(6)C 2.(1)①B C•②DC(或BC)AD⊥BC(2)40°(3)80°或20°(4)12cm2(5)40°3.80°80•° 20°或120°30°30°4.略5.108°6.(1)略(2)①BE∥CD②AF•⊥BE③△ACF≌△ADF④∠BCF=∠EDF等7.说明△BCE≌△AHE,得AH=BC,由等腰三角形的“三线合一”性质得BC=2BD,所以AH=2BD【拓展延伸训练】C【自主探究提高】(1)∠ACB=90°(2)∠ACB=90°(3)猜想:不论∠A•等于多少度(小于90°),∠ACB总等于90°。
等腰三角形练习题(含答案)

等腰三角形第1课时等腰三角形的性质1.已知等腰三角形的一个底角为50。
,则其顶角为________ ・2.如图,HABC中…13=∕C, BC=6cm, JD 平分ZBAC.则BD= _________________ c m.第3题图3.如图,'ABC中,-lδ=FC, D为EC中点,ZBAD=35。
,则ZC的度数为()A.35oB. 45。
C・ 55。
D・ 60o4.已知等腰三角形的一个内角为50。
,则这个等腰三角形的顶角为()A・ 50o B. 80oC. 50。
或80。
D・ 40。
或65。
5.如图,在Z∖J5C 中,D 是BC 边上一点,^AB=.-ID=DC, ZAW=40°,求ZC 的度数.6.如图,ΔJBCΦ, .IB=AC9 D 是EC 的中点,E, F分别是.1B. JC±的点,且AE=AF. 求证:DE=DF.1. 在 ∕∖ABC 中,ZJ=40% Z5 = 70o ,则 MBC 为()A.等腰三角形B.直角三角形C.等腰直角三角形D.钝角三角形2. 已知ΔJPC 中,Z5=50% ZJ = 80c , -lδ=5cm.则 AC= _________________ ・3. 如图,在ΛABC 中,-Q 丄BC 于点Zh 请你再添加一个条件,使苴可以确定AlSC 为等腰三角形,则添加的条件是 ________ ・第3题图4. 如图,已知NlBC 中,ZJ = 36% AB=AC, BD 为ZABC 的平分线,则图中共有 _______________ 个等腰三角形.5. 如图,D 是ZXJ5C 的BC 边上的中点,DE 丄AC. DFLAB.垂足分别是E, F,且DE=DF 求证:AB=AC.6.如图,肋〃 CZ λ直线/交,松于点E,交CD 于点F, FG 平分ZEFD 交直线曲于点G 求证:ZLEFG 是等腰三角形.第4题图13・3.2等边三角形第1课时等边三角形的性质与判定1. ____________________________________________________________ 如图,a∕∕b.等边MBC的顶点D C在直线b上,则Zl的度数为_______________________第1题图第3题图2.在∕∖ABC中,ZJ=60°,现有下面三个条件:®ZB=ZC;③ZA=ZB.能判定Z∖J5C为等边三角形的有____________________________ .3・如图,在等边AABC中,BD丄AC于D∙若,松=4,则AD= ________________ ・4.如图,ΔJ J9C是等边三角形,ZCBD=90°. BD=BC.连接.10交BC于点求ZBAD 的度数.5・如图,E是等边AABC中JC边上的点,Z1 = Z2, BE=CD.求证: (I)ZUEE 竺ZUS⑵AADE为等边三角形.第2课时含30。
等腰三角形专项练习30题(有答案)OK
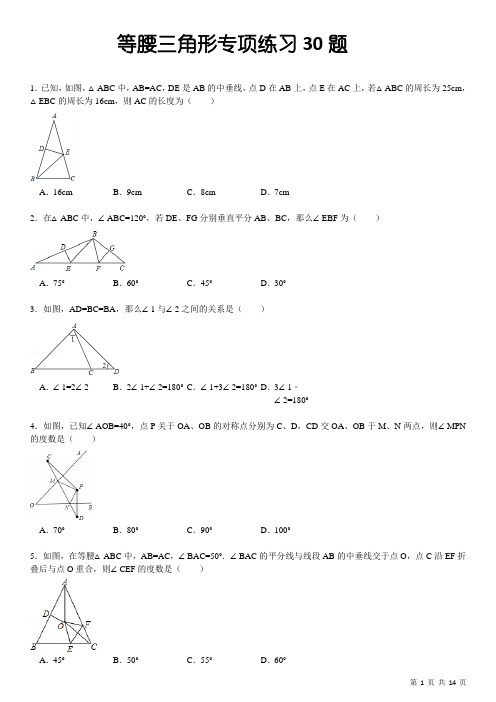
等腰三角形专项练习30题1.已知,如图,△ABC中,AB=AC,DE是AB的中垂线,点D在AB上,点E在AC上,若△ABC的周长为25cm,△EBC的周长为16cm,则AC的长度为()A.16cm B.9cm C.8cm D.7cm2.在△ABC中,∠ABC=120°,若DE、FG分别垂直平分AB、BC,那么∠EBF为()A.75°B.60°C.45°D.30°3.如图,AD=BC=BA,那么∠1与∠2之间的关系是()A.∠1=2∠2 B.2∠1+∠2=180°C.∠1+3∠2=180°D.3∠1﹣∠2=180°4.如图,已知∠AOB=40°,点P关于OA、OB的对称点分别为C、D,CD交OA、OB于M、N两点,则∠MPN的度数是()A.70°B.80°C.90°D.100°5.如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是()A.45°B.50°C.55°D.60°6.如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有()A.B.C.D.7.如图所示,AB=AD,∠ABC=∠ADC=90°,则①AC平分∠BAD;②CA平分∠BCD;③AC垂直平分BD;④BD平分∠ABC,其中正确的结论有()A.①②B.①②③C.①②③④D.②③8.下列说法正确的是()A.两个能重合的图形一定关于某条直线对称B.若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧C.到角两边距离相等的点在这个角的平分线上D.如果三角形一边的垂直平分线经过它的一个顶点,那么这个三角形一定是等腰三角形9.用一根长为a米的线围成一个等边三角形,测知这个等边三角形的面积为b平方米.现在这个等边三角形内任取一点P,则点P到等边三角形三边距离之和为()米.A.B.C.D.10.在等腰直角△ABC(AB=AC≠BC)所在的三角形边上有一点P,使得△PAB,△PAC都是等腰三角形,则满足此条件的点有()A.1个B.3个C.6个D.7个11.如图所示,在△ABC中,AB=AC,腰AB的垂直平分线交另一腰AC于点D,BD+CD=10cm,则AB的长为_________.12.如图,若等腰△ABC的腰长AB=10cm,AB的垂直平分线交另一腰AC于D,△BCD的周长为16cm,则底边BC是_________cm.13.已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是_________.14.如图所示,将两个全等的有一个角为30°的直角三角形拼在一起,其中两条较长直角边在同一条直线上,则图中等腰三角形有_________个.15.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=8,BC=5,则BD的长为_________.16.等腰△ABC的底边上高AD与底角平分线CE交于点P,EF⊥AD,F为垂足,则线段EB与线段EF的数量关系为_________.17.如图,在等腰在△ABC中,AB=27,AB的垂直平分线交AB于点D,交AC于点E,若在△BCE的周长为50,则底边BC的长为_________.18.等腰△ABC中,AB=AC,一腰上的中线BD将这个等腰三角形的周长分成15和6两部分,则这个三角形的腰长为_________.19.如图,已知D为等边三角形纸片ABC的边AB上的点,过点D作DG∥BC交AC于点G,DE⊥BC于点E,过点G作GF⊥BC于点F.把三角形纸片ABC分别沿DG,DE,GF按图示方式折叠,则图中阴影部分是_________三角形.20.如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):_________.21.如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°.求证:△AMN的周长等于2.22.如图所示,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,过点D作DE∥BC交AB于点E,过点D作DF⊥AB于点F,说明:BC=DE+EF成立的理由.23.如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.(1)求证:AD⊥CF;(2)连接AF,试判断△ACF的形状,并说明理由.24.已知:如图,P、Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.25.如图,∠1=∠2,AB=AD,∠B=∠D=90°,请判断△AEC的形状,并说明理由.26.如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,①求证:△BCE≌△ACD;②求证:CF=CH;③判断△CFH的形状并说明理由.27.如图:△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1,求AD的长.28.如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F.(1)证明:∠CAE=∠CBF;(2)证明:AE=BF.29.如图,在△ABC中,已知AB=BC=CA,AE=CD,AD与BE交于点P,BQ⊥AD于点Q,求证:BP=2PQ.30.如图,△ABE和△BCD都是等边三角形,且每个角是60°,那么线段AD与EC有何数量关系?请说明理由.参考答案:1.解:∵DE是AB的垂直平分线,∴AE=BE,∵△ABC的周长为25cm,△EBC的周长为16cm,AC=AB,∴2AC+BC=25cm,BE+CE+BC=AE+EC+BC=AC+BC=16cm,即,解得:AC=9cm,故选B2.解:∵DE、FG分别垂直平分AB、BC,∴AE=BE,BF=CF,∴∠A=∠ABE,∠C=∠CBF,∵∠A+∠C+∠ABC=180°,∠ABC=120°,∴∠A+∠C=60°,∴∠ABE+∠CBF=60°,∴∠EBF=120°﹣60°=60°,故选B3.解:∵AB=BC,∴∠1=∠BCA,∵AB=AD,∴∠B=∠2,∵∠1+∠B+∠ACB=180°,∴2∠1+∠2=180°.故选B4.解:∵P关于OA、OB的对称∴OA垂直平分PC,OB垂直平分PD∴CM=PM,PN=DN∴∠PMN=2∠C,∠PNM=2∠D,∵∠PRM=∠PTN=90°,∴在四边形OTPR中,∴∠CPD+∠O=180°,∴∠CPD=180°﹣40°=140°∴∠C+∠D=40°∴∠MPN=180°﹣40°×2=100°故选D.5.解:如图,延长AO交BC于点M,连接BO,∵等腰△ABC中,AB=AC,∠BAC=50°,∴∠ABC=∠ACB=(180°﹣50°)÷2=65°,∵AO是∠BAC的平分线,∴∠BAO=25°,又∵OD是AB的中垂线,∴∠OBA=∠OAB=25°,∴∠OBM=∠OCM=60°﹣25°=40°,∴∠BOM=∠COM=90°﹣40°=50°,由折叠性可知,∠OCM=∠COE,∴∠MOE=∠COM﹣∠COE=50°﹣40°=10°,∴∠OEM=90°﹣10°=80°,∵由折叠性可知,∠OEF=∠CEF,∴∠CEF=(180°﹣80°)÷2=50°.故选:B6.解:设BM=x,CN=y则BP=2x,PC=2y,PM=x,PN=yAM+AN=2BC﹣(BM+CN)=3(x+y),故==≈0.7887.故选D7.解:在Rt△ABC和Rt△ADC中,AB=AD,AC=AC,所以Rt△ABC≌Rt△ADC(HL).所以∠ACB=∠ACD,∠BAC=∠DAC,即AC平分∠BAD,CA平分∠BCD.故①②正确;在△ABD中,AB=AD,∠BAO=∠DAO,所以BO=DO,AO⊥BD,即AC垂直平分BD.故③正确;不能推出∠ABO=∠CBO,故④不正确.故选B8.解:A、两个能重合的图形不一定关于某条直线对称,故错误;B、两个图形关于某条直线对称,它们的对应点有可能位于对称轴上,故错误;C、同一平面内,到角的两边距离相等的点在角的平分线上,故错误;D,正确,故选D9.解:等边三角形周长为a,则边长为,设P到等边三角形的三边分别为x、y、z,则等边三角形的面积为b=××(x+y+z)解得x+y+z=,故选C10.解:∵△ABC是等腰直角三角形,(AB=AC≠BC)所在的三角形边上有一点P,使得△PAB,△PAC都是等腰三角形,∴有一个满足条件的点﹣斜边中点,∴符合条件的点有1个.故选A.11.解:∵ED是边AB边上的中垂线,∴AD=BD;又∵BD+CD=10cm,AB=AC,∴BD+CD=AD+DC=AC=AB=10cm,即AB=10cm.故答案是:10cm12.解:∵DE是线段AB的垂直平分线,∴AD=BD,∴BD+CD=AC,∵AB=AC=10cm,BD+CD+BC=AB+BC=16cm,∴BC=16﹣AB=16﹣10=6cm.故答案为:6cm13.解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故答案为:2014.解:∵将两个全等的有一个角为30°的直角三角形拼在一起,其中两条较长直角边在同一条直线上.∴EF∥DG,∠E=∠D=60°,∴∠ENM=∠D=60°,∠MGD=∠E=60°,∴EM=NM=EN,DM=GM=DG,∴△MEN,△MDG是等边三角形.∵∠A=∠B=30°,∴MA=MB,∴△ABM是等腰三角形.∴图中等腰三角形有3个15.解:延长BD与AC交于点E,∵∠A=∠ABD,∴BE=AE,∵BD⊥CD,∴BE⊥CD,∵CD平分∠ACB,∴∠BCD=∠ECD,∴∠EBC=∠BEC,∴△BEC为等腰三角形,∴BC=CE,∵BE⊥CD,∴2BD=BE,∵AC=8,BC=5,∴CE=5,∴AE=AC﹣EC=8﹣5=3,∴BE=3,∴BD=1.5.故选A.16.解:延长EF交AC于点Q,∵EF⊥AD,AD⊥BC∴EQ∥BC∴∠QEC=∠ECB∵CE平分∠ACB∴∠ECB=QCE∴∠QEC=∠QCE∴QE=QC∵QE∥BC,且△ABC为等腰三角形∴△AQE为等腰三角形∴AQ=AE,QE=2EF∴BE=CQ=2EF.故答案为:BE=2EF.17.解:∵DE垂直且平分AB,∴BE=AE.由BE+CE=AC=AB=27,∴BC=50﹣27=2318.解:设AB=AC=2X,BC=Y,则AD=CD=X,∵AC上的中线BD将这个三角形的周长分成15和6两部分,∴有两种情况:1、当3X=15,且X+Y=6,解得,X=5,Y=1,∴三边长分别为10,10,1;2、当X+Y=15且3X=6时,解得,X=2,Y=13,此时腰为4,根据三角形三边关系,任意两边之和大于第三边,而4+4=8<13,故这种情况不存在.∴腰长只能是10.故答案为1019.解:∵三角形ABC为等边三角形,∴∠A=∠B=∠C=60°,∵根据题意知道点B和点C经过折叠后分别落在了点I和点H处,∴∠DIH=∠B=60°,∠GHI=∠C=60°,∴∠HJI=60°,∴∠DIH=∠GHI=∠HJI=60°,∴阴影部分是等边三角形,故答案为:等边.20.答:由①③条件可判定△ABC是等腰三角形.证明:∵∠EBO=∠DCO,∠EOB=∠DOC,(对顶角相等)BE=CD,∴△EBO≌△DCO,∴OB=OC,∴∠OBC=∠OCB,∴∠ABC=∠ACB,∴△ABC是等腰三角形21.解:延长AC到E,使CE=BM,连接DE,(如图)∵BD=DC,∠BDC=120°,∴∠CBD=∠BCD=30°,∵∠ABC=∠ACB=60°,∴∠ABD=∠ACD=∠DCE=90°,∴△BMD≌△CDE,∴∠BDM=∠CDE,DM=DE,又∵∠MDN=60°,∴∠BDM+∠NDC=60°,∴∠EDC+∠NDC=∠NDE=60°=∠NDM,又∵DN=DN,∴△MDN≌△EDN(SAS),∴MN=NE=NC+CE=NC+BM,所以△AMN周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2.22.解:∵BD平分∠ABC,DF⊥AB,∠C是直角,∴CD=DF,∠DBC=∠DBE,∠DFB=∠C,∴△BCD≌△BFD,∴BC=BF,∵DE∥BC,∴∠DBC=∠EDB,即∠DBC=∠DBE,∴△BDE是等腰三角形,∴BE=DE,∴BF=BC=DE+EF23.(1)证明:在等腰直角三角形ABC中,∵∠ACB=90°,∴∠CBA=∠CAB=45°.又∵DE⊥AB,∴∠DEB=90°.∴∠BDE=45°.又∵BF∥AC,∴∠CBF=90°.∴∠BFD=45°=∠BDE.∴BF=DB.又∵D为BC的中点,∴CD=DB.即BF=CD.在△CBF和△ACD中,,∴△CBF≌△ACD(SAS).∴∠BCF=∠CAD.又∵∠BCF+∠GCA=90°,∴∠CAD+∠GCA=90°.即AD⊥CF.(2)△ACF是等腰三角形,理由为:连接AF,如图所示,由(1)知:CF=AD,△DBF是等腰直角三角形,且BE是∠DBF的平分线,∴BE垂直平分DF,∴AF=AD,∵CF=AD,∴CF=AF,∴△ACF是等腰三角形.24.解:∵BP=PQ=QC=AP=AQ,∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,∴∠BAP=∠CAQ=30°.∴∠BAC=120°.故∠BAC的度数是120°25.解:△AEC是等腰三角形.理由如下:∵∠1=∠2,∴∠1+∠3=∠2+∠3,即∠BAC=∠DAE,又∵AB=AD,∠B=∠D,∴△ABC≌△ADE(ASA),∴AC=AE.即△AEC是等腰三角形26.①证明:∵∠BCA=∠DCE=60°,∴∠BCE=∠ACD,在△BCE和△ACD中,,∴△BCE≌△ACD(SAS);②∵△BCE≌△ACD,∴∠CBF=∠CAH.∵∠ACB=∠DCE=60°,∴∠ACH=60°.∴∠BCF=∠ACH,在△BCF和△ACH中,,∴△BCF≌△ACH(ASA),∴CF=CH;③∵CF=CH,∠ACH=60°,∴△CFH是等边三角形27.解:∵△ABC为等边三角形,∴AB=CA,∠BAE=∠ACD=60°;又∵AE=CD,在△ABE和△CAD中,∴△ABE≌△CAD;∴BE=AD,∠CAD=∠ABE;∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°;∵BQ⊥AD,∴∠AQB=90°,则∠PBQ=90°﹣60°=30°;∵PQ=3,∴在Rt△BPQ中,BP=2PQ=6;又∵PE=1,∴AD=BE=BP+PE=728.(1)证明:在等腰△ABC中,∵CH是底边上的高线,∴∠ACH=∠BCH,在△ACP和△BCP中,,∴△ACP≌△BCP(SAS),∴∠CAE=∠CBF(全等三角形对应角相等);(2)在△AEC和△BFC中,∴△AEC≌△BFC(ASA),∴AE=BF(全等三角形对应边相等).29.证明:∵AB=BC=CA,∴△ABC为等边三角形,∴∠BAC=∠C=60°,在△ABE和△CAD中∴△ABE≌△CAD(SAS),∴∠ABE=∠CAD,∵∠BPQ=∠ABE+∠BAP,∴∠BPQ=∠CAD+∠BAP=∠CAB=60°,∵BQ⊥AD∴∠BQP=90°,∴∠PBQ=30°,∴BP=2PQ.30.解:AD=EC.证明如下:∵△ABC和△BCD都是等边三角形,每个角是60°∴AB=EB,DB=BC,∠ABE=∠DBC=60°,∴∠ABE+∠EBC=∠DBC+∠EBC即∠ABD=∠EBC在△ABD和△EBC中∴△ABD≌△EBC(SAS)∴AD=EC。
八年级数学等腰三角形(习题及答案)

等腰三角形(习题)例题示范例1:如图,在△ABC 中,AB =AC ,点D 在△ABC 外,CD ⊥AD 于点D ,12CD BC =.求证:∠ACD =∠B . 【思路分析】① 读题标注:② 梳理思路: 由条件12CD BC =,可尝试取BC 的中点E ,此时结合等腰构造三线合一的线AE ,如图所示.要证∠ACD =∠B ,可以证明△ABE ≌△ACD .【过程书写】证明:如图,取BC 的中点E ,连接AE .∵E 是BC 的中点 ∴12BE BC = ∵12CD BC = ∴BE =CD∵AB =AC ,E 是BC 的中点∴AE ⊥BC∴∠AEB =90°∵CD ⊥AD∴∠D =90°∴∠AEB =∠D =90°在Rt △ABE 和Rt △ACD 中AB AC BE CD =⎧⎨=⎩(已知)(已证)∴Rt △ABE ≌Rt △ACD (HL )∴∠ACD =∠B例2:等腰三角形的周长为12cm ,其中一边长为5cm ,则该等腰三角形的底边长为__________cm .AC D【思路分析】等腰三角形一边长为5cm,这一边可能是底,也可能是腰,故需分类讨论:①如果5cm为底,则根据周长为12cm,可知腰长为3.5cm.此时两边之和大于第三边,这个三角形存在.②如果5cm为腰,则根据周长为12cm,可知底边长为2cm.此时两边之和大于第三边,这个三角形存在.综上,该等腰三角形的底边长为5cm或2cm.巩固练习1.已知:如图,在△ABC中,AB=AC,∠A=80°,求∠C的度数.2.如图,在△ABC中,AB=AC,BE∥AC,∠BDE=100°,∠BAD=70°,则∠E=______.第2题图第3题图3.已知:如图,在△ABC中,AB=AC,D为AB边上一点,若CD=AD=BC,则∠A=_________.4.如图,在△ABC中,∠ABC的平分线和∠ACB的平分线相交于点E,过点E作MN∥BC,交AB于点M,交AC于点N.若BM+CN=9,则线段MN的长为()A.6 B.7 C.8 D.95.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点P在AD上.求证:PB=PC.6.已知:如图,B,D,E,C在同一直线上,AB=AC,AD=AE.求证:BD=CE.7.已知等腰三角形的两边长分别为4和8,则该等腰三角形的周长为_________________.8.若等腰三角形的一个角比另一个角大30°,则该等腰三角形的顶角的度数为_____________.9.已知:如图,线段AB的端点A在直线l上,AB与l的夹角是30°,请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请找出所有符合条件的点.思考小结1.要证明边相等或角相等,可以考虑两种思路:①如果边或者角在两个三角形里面,则证明两个三角形__________;②如果边或角在一个三角形里面,证明三角形是_______三角形.2.将两个含30°角的三角板如图放置,则△ABD是_________三角形(“等腰”或“等边”),故AB_____BD,BC=____BD,所以BC=____AB,从而得到对于含有30°角的直角三角形,30°角所对的直角边是斜边的_______.【参考答案】巩固练习1.50°2.50°3.36°4. D5.证明略提示:利用等腰三角形三线合一的性质,得AD垂直平分BC,从而得到PB=PC 6.证明略提示:根据等边对等角可得∠B=∠C,∠ADE=∠AED,进而可得∠BAD=∠CAE,从而证明△ABD≌△ACE,根据全等三角形对应边相等,可得BD=CE7.208.80°或40°9.这样的点能找4个,作图略 思考小结1.①全等②等腰2.等边,=,12,12,一半。
等腰三角形典型例题
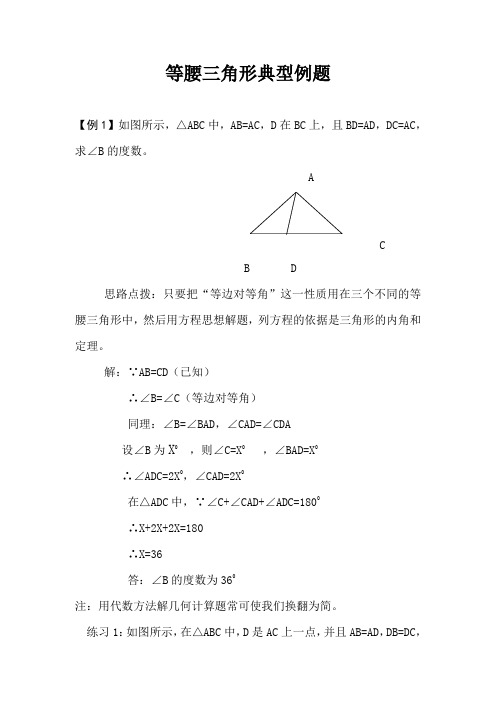
等腰三角形典型例题【例1】如图所示,△ABC中,AB=AC,D在BC上,且BD=AD,DC=AC,求∠B的度数。
ACB D思路点拨:只要把“等边对等角”这一性质用在三个不同的等腰三角形中,然后用方程思想解题,列方程的依据是三角形的内角和定理。
解:∵AB=CD(已知)∴∠B=∠C(等边对等角)同理:∠B=∠BAD,∠CAD=∠CDA设∠B为X0,则∠C=X0,∠BAD=X0∴∠ADC=2X0,∠CAD=2X0在△ADC中,∵∠C+∠CAD+∠ADC=1800∴X+2X+2X=180∴X=36答:∠B的度数为360注:用代数方法解几何计算题常可使我们换翻为简。
练习1:如图所示,在△ABC中,D是AC上一点,并且AB=AD,DB=DC,若∠C=290,则∠A=___练习2:如图在△ABC 中,AB=AC,点D 在AC 上,且BD=BC=AD,求△ABC 各角的度数?【例2】如图所示,在△ABC 中,AB=AC ,O 是△ABC 内一点,且OB=OC 。
求证:AO ⊥BC思路点拨:要证AO ⊥BC ,即证AO是等腰三角形底边上的高,根据三线合一定理,只要先证AO 是顶角的平分线即可。
B证明:延长AO 交BC 于DAB=AC (已知) 在△ABO 和△ACO 中 OB=OC (已知) AO=AO(公共边) ∴△ABO ≌△ACO (SSS ) ∴∠BAO=∠CAO即∠BAD=∠CAD (全等三角形的对应角相等)∴AD ⊥BC ,即AO ⊥BC (等腰三角形顶角的平分线与底边上的高互相重合)评注:本题用两次全等也可达到目的.。
练习:如图所示,点D 、E 在△ABC 的边BC 上,AB=AC ,AD=AE 求证:BD=CE【例3】求证等腰三角形底边上任一点到两腰的距离之和等于一腰上C的高。
思路点拨:本题为文字题,文字题必须按下列步骤进行:(1)根据题意画出图形;(2)根据图形写出“已知”、“求证”;(3)写出证明过程。
等腰三角形经典练习题(5套)附带详细答案

练习一一、选择题1.等腰三角形的周长为26㎝,一边长为6㎝,那么腰长为()A.6㎝B.10㎝C.6㎝或10㎝D.14㎝2.已知△ABC,AB =AC,∠B=65°,∠C度数是( )A.50°B.65°C.70°D.75°3.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边的垂线C.顶角的平分线所在的直线D.腰上的高所在的直线二、填空题4.等腰三角形的两个_______相等(简写成“____________”).5.已知△ABC,AB =AC,∠A=80°,∠B度数是_________.6.等腰三角形的两个内角的比是1:2,则这个等腰三角形的顶角的度数是_______________.7.等腰三角形的腰长是6,则底边长5,周长为__________.三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.(写出每步证明的重要依据)9.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数一、选择题1.B2.B3.C二、填空题4.底角,等边对等角5.50°6.36°或90°7.16或17三、解答题8.如图AB=AD,AD∥BC,求证:BD平分∠ABC.证明:∵AB=AD(已知)∴∠ABD=∠ADB(等边对等角)∵AD∥BC(已知)∴∠ADB=∠CBD(两直线平行,内错角相等)∴∠ABD=∠CBD(等量代换)∴BD平分∠ABC.(角平分线定义)9.45练习2一、选择题1.△ABC是等边三角形,D、E、F为各边中点,则图中共.有正三角形( )A.2个B.3个C.4个D.5个2.△ABC中,∠A:∠B:∠C=1:2:3,则BC:AB等于( )A.2:1 B.1:2 C.1:3 D.2 :3二、填空题3.等边三角形的周长为6㎝,则它的边长为________.4.等边三角形的两条高线相交所成钝角的度数是__________.5.在△ABC中,∠A=∠B=∠C,则△ABC是_____三角形.6.△ABC中,∠AC B=90°∠B=60°,BC=3㎝,则AB=_______.三、解答题7.△ABC是等边三角形,点D在边BC上,DE∥AC,△BDE是等边三角形吗?试说明理由.8.已知:如图,P,Q是△ABC边上BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.9.已知:△ABC中,∠ACB=90°,AD=BD,∠A=30°,求证:△BDC是等边三角形.一、选择题1.D2.B二、填空题3.2㎝4.120°5.等边6.6㎝三、解答题7.△ABC是等边三角形.理由是∵△ABC是等边三角形AQ CPB∴∠A =∠B =∠C=60° ∵DE ∥AC ,∴∠BED =∠A=60°,∠BDE =∠C =60° ∴∠B =∠BED =∠BDE ∴△ABC 是等边三角形 8.∠BAC=120°9.证明:∵△ABC 中,∠ACB=90°,∠A=30°(已知)∴∠A +∠B=90°(直角三角形两锐角互余) ∴∠B= 90°-∠A= 90°-30°=60° ∵△ABC 中,∠ACB=90°,∠A=30°(已知) ∴BC=(在直角三角形中,一个锐角等于30,那么它所对的直角边等于斜边的一半)∴△BDC 是等边三角形(有一个角是60°角的等腰三角形是等边三角形)。
等腰三角形习题(含答案)
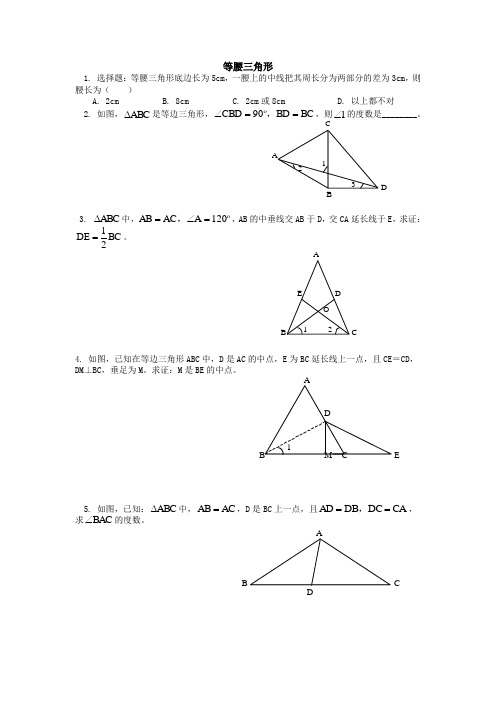
等腰三角形1. 选择题:等腰三角形底边长为5cm ,一腰上的中线把其周长分为两部分的差为3cm ,则腰长为( )A. 2cmB. 8cmC. 2cm 或8cmD. 以上都不对 2. 如图,ABC ∆是等边三角形,BC BD 90CBD ==∠,,则1∠的度数是________。
CA 1DB2 33. ABC ∆中,120A AC AB =∠=,,AB 的中垂线交AB 于D ,交CA 延长线于E ,求证:BC 21DE =。
AE DO BC1 24. 如图,已知在等边三角形ABC 中,D 是AC 的中点,E 为BC 延长线上一点,且CE =CD ,DM ⊥BC ,垂足为M 。
求证:M 是BE 的中点。
A D 1B MC E5. 如图,已知:ABC ∆中,AC AB =,D 是BC 上一点,且CA DC DB AD ==,,求BAC ∠的度数。
AB C D6. 已知:如图,ABC ∆中,AB CD AC AB ⊥=,于D 。
求证:DCB 2BAC ∠=∠。
A 1 2D BCE 37、已知:如图,在△ABC 中,AB =AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,E 、F 分别是垂足。
求证:AE =AF 。
AE FBDC8、如图,ABC ∆中,100=∠=A AC AB ,,BD 平分ABC ∠。
求证:BC BD AD =+。
AD1 B 2E FC等腰三角形答案:1. B2. 分析:结合三角形内角和定理,计算图形中角的度数是等边三角形性质的重要应用。
解:因为ABC ∆是等边三角形 所以60ABC BC AB =∠=,因为BC BD =,所以BD AB = 所以23∠=∠在ABD ∆中,因为 60ABC 90CBD =∠=∠, 所以 150ABD =∠,所以152=∠ 所以75ABC 21=∠+∠=∠3.分析:此题没有给出图形,那么依题意,应先画出图形。
题目中是求线段的倍半关系,观察图形,考虑取BC 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形典型例题练习等腰三角形典型例题练习一•选择题(共2小题)1 如图,/ C=90° AD平分/ BAC交BC于D,若BC=5cm , BD=3cm,则点D到AB的距离为()2. 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC 为边并且在AB的同一侧作等边△ ACD 和等边△BCE,连接AE交CD于M,连接BD交CE于N .给出以下三个结论:①AE=BD②CN=CM③MN // AB其中正确结论的个数是()A. 0 B . 1 |C. 2 D. 3二.填空题(共1小题)3. ______________________________________ 如图,在正三角形ABC中,D, E, F分别是BC, AC , AB上的点,DE 丄AC , EF丄AB , FD丄BC ,则△ DEF 的面积与△ ABC的面积之比等于.5. 在△ ABC中,/ ABC、/ ACB的平分线相交于点0,过点0作DE // BC,分别交AB、AC于点D、E.请说明DE=BD+EC .B • 3 cm C. 2cm D.不能确定三.解答题(共15小题)4.在厶ABC中,AD是/ BAC的平分线, E、F分别为AB、AC上的点,且/ EDF+ / EAF=180 °求证DE=DF .A • 5cm6. >已知:如图,D是厶ABC的BC边上的中点,DE丄AB , DF丄AC ,垂足分别为E, F,且DE=DF .请判断△ ABC 是什么三角形?并说明理由.7. 如图,△ ABC是等边三角形,BD是AC边上的高,延长BC至E,使CE=CD .连接DE .(1)Z E等于多少度?(2)△ DBE是什么三角形?为什么?&如图,在△ ABC 中,/ ACB=90 ° CD 是AB 边上的高,/ A=30 ° 求证:AB=4BD .9.如图,△ ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且BD=CE , DE与BC相交于点F.求证: DF=EF .10 .已知等腰直角三角形ABC , BC是斜边./ B的角平分线交AC于D,过C作CE与BD垂直且交BD延长线于E,求证:BD=2CE .11. (2012?牡丹江)如图①,△ ABC中.AB=AC , P为底边BC上一点,PE丄AB , PF丄AC , CH丄AB,垂足分别为E、F、H.易证PE+PF=CH .证明过程如下:如图①,连接AP.•/ PE丄AB , PF丄AC , CH 丄AB ,二S^ABP= AB?PE, S A ACP= AC?PF, S A ABC=—AB?CH .2 2 2又T ABP+S A ACP=S A ABC ,••• _AB ?PE+丄AC ?PF= AB ?CH .2 2 2•/ AB=AC ,• PE+PF=CH .(1)如图②,P为BC延长线上的点时,其它条件不变,PE、PF、CH又有怎样的数量关系?请写出你的猜想,并加以证明:(2)填空:若/ A=30 ° △ ABC的面积为49,点P在直线BC上,且P到直线AC的距离为PF,当PF=3时,则AB边上的高CH= ______________ .点P到AB边的距离PE= _______________ .12•数学课上,李老师出示了如下的题目:在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE _________________ DB (填\ ”,或=”).(2 )特例启发,解答题目解:题目中,AE与DB的大小关系是:AE _________________ D B (填\”,N ”或=”).理由如下:如图2,过点E作EF // BC,交AC于点F.(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC .若△ ABC的边长为1, AE=2,求CD的长(请你直接写出结果). 仝〔国一13. 已知:如图,AF平分/ BAC , BC丄AF于点E,点D在AF上,ED=EA,点P在CF上,连接PB交AF于点M .若/ BAC=2 / MPC,请你判断/ F与/ MCD的数量关系,并说明理由.14. 如图,已知△ ABC是等边三角形,点D、E分别在BC、AC边上,且AE=CD , AD与BE相交于点F.(1)线段AD与BE有什么关系?试证明你的结论.(2)求/ BFD的度数.15. 如图,在△ ABC中,AB=BC,/ ABC=90 ° F为AB延长线上一点,点E在BC上,BE=BF,连接AE、EF 和CF,求证:AE=CF .16. 已知:如图,在△ OAB 中,/ AOB=90 ° OA=OB,在△ EOF 中,/ EOF=90 ° OE=OF,连接AE、BF .问线段AE与BF之间有什么关系?请说明理由.I)17. (2006?郴州)如图,在 △ ABC 中,AB=AC , D 是BC 上任意一点,过 D 分别向AB , AC 引垂线,垂足分别为 E , F ,CG 是AB 边上的高.(1) DE , DF , CG 的长之间存在着怎样的等量关系?并加以证明;(2) 若D 在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?请说明理由.18. 如图甲所示,在 △ ABC 中,AB=AC ,在底边BC 上有任意一点P ,贝U P 点到两腰的距离之和等于定长(腰上 的高),即PD+PE=CF ,若P 点在BC 的延长线上,那么请你猜想 PD 、PE 和CF 之间存在怎样的等式关系?写出你 的猜想并加以证明.等腰三角形典型例题练习参考答案与试题解析一•选择题(共2小题)1 如图,/ C=90° AD平分/ BAC交BC于D,若BC=5cm , BD=3cm,则点D到AB的距离为()2. 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ ACD 和等边△BCE,连接AE交CD于M,连接BD交CE于N .给出以下三个结论:①AE=BD②CN=CM③MN // AB其中正确结论的个数是()A. 0 B . 1 |C. 2 D. 3考点:平行线分线段成比例;全等三角形的判定与性质;等边三角形的性质.分析:由厶ACD和厶BCE是等边三角形,根据SAS易证得△ ACE ◎△ DCB,即可得① 正确;由△ACE DCB,可得/ EAC= / NDC,又由/ ACD= / MCN=60 ° 利用ASA,可证得△ACM ◎△ DCN,即可得② 正确;又可证得△ CMN是等边三角形,即可证得③ 正确.解答:解:•••△ ACD 和厶BCE 是等边三角形,•/ ACD= / BCE=60 ° AC=DC , EC=BC ,•••/ ACD+ / DCE= / DCE+ / ECB,即/ ACE= / DCB , •△ ACE DCB (SAS),• AE=BD,故①正确;•••/ EAC= / NDC ,•••/ ACD= / BCE=60 ° DCE=60 ° ACD= / MCN=60 °•/ AC=DC ACM ◎△ DCN (ASA) , • CM=CN,故② 正确;又/ MCN=180 °-Z MCA -/ NCB=180。
- 60°- 60°=60°•△ CMN是等边三角形,•/ NMC= / ACD=60 ° • MN // AB,故③正确.故选 D .二.填空题(共1小题)3. 如图,在正三角形ABC中,D, E, F分别是BC, AC , AB上的点,DE丄AC , EF 丄AB , FD丄BC ,则△ DEF 的面积与△ ABC的面积之比等于1: 3 .B • 3 cm C. 2cm D.不能确定考点:解答:角平分线的性质.由已知条件进行思考,结合利用角平分线的性质可得点的长,问题可解.解:I/ C=90° AD 平分/ BAC 交BC 于 D••• D至U AB的距离即为CD长CD=5 - 3=2故选C.D到AB的距离等于D到AC的距离即CDA • 5cm考点:相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的性质.分析:首先根据题意求得: / DFE= / FED= / EDF=60 °即可证得△ DEF是正三角形,又由直角三角形中,30°所对的直角边是斜边的一半,得到边的关系,即可求得DF : AB=1 : ,又由相似三角形的面积比等于相似比的平方,即可求得结果.解答:解:•••△ ABC 是正三角形,•••/ B= / C= / A=60 °•/ DE 丄AC , EF丄AB , FD 丄BC,• / AFE= / CED= / BDF=90 °•••/ BFD= / CDE= / AEF=30 ° DFE= / FED= / EDF=60 ° 型丄BF 2• △ DEF 是正三角形,• BD : DF=1 :黃①,BD: AB=1 : 3②,△ DEFABC ,①十②,冬忑,• DF : AB=1 : DEF的面积与△ ABC的面积之比等于1: 3.考点:全等三角形的判定与性质;角平分线的定义.过D作DM丄AB,于M , DN丄AC于N,根据角平分线性质求出DN=DM,根据四边形的内角和定理和平角定义求出/ AED= / CFD,根据全等三角形的判定证明:过D作DM丄AB,于M , DN丄AC于N ,•/ AD 平分/ BAC , DM 丄AB , DN 丄AC , • DM=DN (角平分线性质),/ DME= / DNF=90 °•••/ EAF+ / EDF=180 °MED+ / AFD=360 °- 180 °180 °•••/ AFD+ / NFD=180 °MED= / NFD ,在厶EMD和△ FND中f ZMED=ZDFN三•解答题(共15小题)4.在厶ABC中,AD是/ BAC的平分线, E、F分别为AB、AC上的点,且/ EDF+ / EAF=180 °求证DE=DF .分析:解答:AAS 推出△ EMD ◎△ FND 即可.* ZDME=ZDNF,•△ EMD ◎△FND ,••• DE=DF .DM=DNL5. 在△ ABC中,/ ABC、/ ACB的平分线相交于点O,过点O作DE // BC,分别交AB、AC于点D、E.请说明DE=BD+EC .B C考点:等腰三角形的判定与性质;平行线的性质.分析:根据OB和0C分别平分/ ABC和/ ACB ,和DE // BC ,利用两直线平行,内错角相等和等量代换, 求证出DB=DO,OE=EC .然后即可得出答案.解答:解:•••在△ ABC中,0B和0C分别平分/ ABC和/ACB ,•••/ DBO= / OBC ,Z ECO= / OCB ,•••DE // BC,•/ DOB= / OBC= / DBO,/ EOC= / OCB= / ECO ,• DB=DO , OE=EC,: DE=DO+OE , • DE=BD+EC .6. >已知:如图,D是厶ABC的BC边上的中点,DE丄AB , DF丄AC ,垂足分别为E, F,且DE=DF .请判断△ ABC 是什么三角形?并说明理由.考点:等腰三角形的判定;全等三角形的判定与性质.分析:用(HL )证明△ EBD FCD,从而得出/ EBD= / FCD,即可证明△ ABC是等腰三角形.解答:△ ABC是等腰三角形.证明:连接AD,: DE 丄AB , DF 丄AC,•/ BED= / CFD=90 ° 且DE=DF ,•/ D是厶ABC的BC边上的中点,• BD=DC ,• Rt△ EBD也Rt△ FCD (HL ) , EBD= / FCD , •△ ABC 是等腰三角形.7. 如图,△ ABC是等边三角形,BD是AC边上的高,延长BC至E ,使CE=CD .连接DE .(1) z E 等于多少度? ( 2) △ DBE 是什么三角形?为什么?考点:等边三角形的性质;等腰三角形的判定. 分析: (1 )由题意可推出/ ACB=60 ° Z E=Z CDE ,然后根据三角形外角的性质可知:/ ACB= / E+ / CDE , 即可推出/ E 的度数;(2)根据等边三角形的性质可知, BD 不但为AC 边上的高,也是Z ABC 的角平分线,即得: Z DBC=30 °然后再结合(1)中求得的结论,即可推出 △ DBE 是等腰三角形.解答:: 解: (1):公 ABC 是等边三角形,•••/ ACB=60 ° •••CD=CE ,•/ E = Z CDE ,•••/ ACB = Z E+Z CDE ,•〕「 ■- - i -,(2)•••△ ABC 是等边三角形,BD 丄AC ,「.Z ABC=60 ° • ZDBC 一2乙粧(>3(?, 2vZ E=30° z.Z DBC= Z E ,•△ DBE 是等腰三角形.&如图,在 △ ABC 中,/ ACB=90 ° CD 是 AB 边上的高,/ A=30 ° 求证:AB=4BD .考点:含30度角的直角三角形. 分析:由厶ABC 中,Z ACB=90 ° Z A=30可以推出AB=2BC ,同理可得 BC=2BD ,则结论即可证明. 解答: 解:vZ ACB=90 ° Z A=30 ° • AB=2BC , Z B=60 °又 v CD 丄 AB ,•••/ DCB=30 ° • BC=2BD . • AB=2BC=4BD .9.如图,△ ABC 中,AB=AC ,点D 、E 分别在 AB 、AC 的延长线上,且 BD=CE, DE 与BC相交于点F .求证: DF=EF .在^ DFG 和厶EFC中r Z4=Z3ZDFG 二 Z^FC ,二△ DFG ◎△ EFC ,.・. DF=EF .L DG=CE10 .已知等腰直角三角形 ABC , BC 是斜边./ B 的角平分线交 AC 于D ,过C 作CE 与BD 垂直且交BD 延长线 于E , 求证:BD=2CE .延长CE , BA 交于一点F ,由已知条件可证得 △ BFE 全也△ BEC ,所以FE=EC ,即CF=2CE ,再通 过证明△ ADB FAC 可得 FC=BD ,所以 BD=2CE . 证明:如图,分别延长 CE , BA 交于一点F .•/ BE 丄 EC ,:/ FEB= / CEB=90 ° •/ BE 平分/ ABC ,二/ FBE= / CBE , 又••• BE=BE ,•••△ BFE ◎△ BCE (ASA ) . FE=CE . : CF=2CE .•/ AB=AC , / BAC=90 ° / ABD+ / ADB=90 ° / ADB= / EDC , •/ ABD+ / EDC=90 ° 又•••/ DEC=90 ° / EDC+ / ECD=90 ° , FCA= / DBC= / ABD . • △ ADB ◎△ AFC . • FC=DB , • BD=2EC .11. (2012?牡丹江)如图 ①,△ ABC 中.AB=AC , P 为底边BC 上一点,PE 丄AB , PF 丄AC , CH 丄AB ,垂足分 别为E 、F 、H .易证PE+PF=CH .证明过程如下: 如图①,连接AP .••• PE 丄AB , PF 丄 AC , CH 丄 AB , • S ^ABP = AB ?PE , S ^ACP ==AC?PF , S ^ABC = ,AB ?CH .疋•匕疋又T ABP +S A ACP =S A ABC ,• =AB ?p E+ AC?p F==A B ?CH . •/ AB=AC , • PE+PF=CH .分析: 解答:£考点: 全等三角形的判定与性质.(1)如图②,P为BC延长线上的点时,其它条件不变,PE、PF、CH又有怎样的数量关系?请写出你的猜想,并加以证明:(2)填空:若/ A=30 ° △ ABC的面积为49,点P在直线BC上,且P到直线AC的距离为PF,当PF=3时,则AB边上的高CH= 7 .点P到AB边的距离PE= 4 或10 .考点:等腰三角形的性质;三角形的面积.分析:(1 )连接AP •先根据三角形的面积么式分别表示出S^AB P , S^ACP , S^ABC,再由S A ABP=S A ACP+S A ABC即可得出p E=p F+p H ;(2)先根据直角三角形的性质得出AC=2CH ,再由△ ABC的面积为49,求出CH=7 ,由于CH > PF, 则可分两种情况进行讨论:①P为底边BC上一点,运用结论PE+PF=CH ;②P为BC延长线上的点时,运用结论PE=PF+CH .解答:解: (1)如图②,PE=PF+CH .证明如下::PE 丄AB , PF 丄AC, C H丄AB …S“Bp*B?p E, 5气沖,$△ "?曲, •/ S A ABP=S A ACP+S△ ABC,二丄AB?PE」AC?PF+丄AB?CH,又T AB=AC , A PE=PF+CH ;2 2 2(2)•••在△ ACH 中,/ A=30 ° A AC=2CH .T S A AB C气AB?CH , AB=AC ,A *X2CH?CH=49 , A CH=7 .分两种情况:①P为底边BC上一点,如图①.•/ PE+PF=CH , A PE=CH - PF=7 - 3=4;②P为BC延长线上的点时,如图②.• PE=PF+CH , A PE=3+7=10 .故答案为7; 4 或10.A 4圍①图②12 •数学课上,李老师出示了如下的题目:在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况,探索结论过A 作AM 丄BC 于M ,过E 作EN 丄BC 于N ,贝U AM // EM , •/△ ABC 是等边三角形,••• AB=BC=AC=1 ,•/ AM 丄 BC ,• BM=CM= —BC= —, v DE=CE , EN 丄 BC , • CD=2CN , 2 2当点E 为AB 的中点时,如图1,确定线段AE 与DB 的大小关系,请你直接写出结论: AE或=”).(2 )特例启发,解答题目解:题目中,AE 与DB 的大小关系是:AE 交AC 于点F .(请你完成以下解答过程) (3)拓展结论,设计新题 在等边三角形ABC 中,点DB (填 E 在直线AB 上,点D 在直线DB (填、”,N”的长(请你直接写出结果) 考点: 分析:解答:、”,之”或=”).理由如下:如图2,过点 BC 上,且ED=EC .若△ ABC 的边长为1,E 作 EF // BC ,AE=2,求 CD等边三角形的判定与性质;三角形的外角性质;全等三角形的判定与性质;等腰三角形的性质. O(1)根据等边三角形性质和等腰三角形的性质求出/ D= / ECB=30 °求出/ DEB=30 °求出BD=BE即可;(2 )过E 作EF // BC 交AC 于F ,求出等边三角形 AEF ,证△ DEB 和厶ECF 全等,求出BD=EF 即 可; (3)当D 在CB 的延长线上,E 在AB 的延长线式时, 由(2)求出CD=3,当E 在BA 的延长线上, D 在BC 的延长线上时,求出 CD=1 .解:(1)故答案为:(2)过 E 作 EF // BC 交 AC 于 F ,•••等边三角形 ABC ,•/ ABC= / ACB= / A=60 ° AB=AC=BC , •••/ AEF= / ABC=60 ° / AFE= / ACB=60 ° 即/ AEF= / AFE= / A=60 °, • △ AEF 是等边三角形,• AE=EF=AF ,•••/ ABC= / ACB= / AFE=60 ° DBE= / EFC=120 ° / D+ / BED= / FCE+ / ECD=60 ° ° •/ DE=EC ,•/ D= / ECD ,•/ BED= / ECF , 在厶DEB 和厶ECF 中f ZDEB=ZECF* ZDBE=ZEFC ,^^ DEB ECF ,••• BD=EF=AE ,即 AE=BD ,故答案为:=.L DE=CE(3) 解:CD=1 或 3,理由是:分为两种情况:①如图1D2•/ AM // EN ,•••△ AMB s\ ENB , ••上 ___________ =,BE BW 2-1 BNB ~~c ~~b圏2②如图2,作AM 丄BC 于M ,过E 作EN 丄BC 于N , 贝U AM // EM , •/△ ABC 是等边三角形,• AB=BC=AC=1 ,•/ AM 丄 BC ,• BM=CM= _BC=_, v DE=CE , EN 丄 BC , • CD=2CN ,•/AM // EN ,•“ = ',•••=,• MN=1 ,• CN=1 - = , • CD=2CN=113. 已知:如图, AF 平分/ BAC , BC 丄AF 于点E ,点D 在AF 上,ED=EA ,点P 在CF 上,连接PB 交AF 于点 M .若/ BAC=2 / MPC ,请你判断/ F 与/ MCD 的数量关系,并说明理由.理由是:v AF 平分/ BAC , BC 丄 AF ,•/ CAE= / BAE ,/ AEC= / AEB=90 ° 在厶ACE 和厶ABE 中AE MN考点:全等三角形的判定与性质;等腰三角形的性质.根据全等三角形的性质和判定和线段垂直平分线性质求出AB=AC=CD ,推出/ CDA= / CAD= / CPM ,求出/ MPF= / CDM ,/ PMF= / BMA= / CMD ,在△ DCM 和△ PMF 中 根据三角形的内角和定理求出即可. 解答:解:/ F= / MCD ,• BN= ,••• CN=1 + *£ ,••• CD=2CN=3 ;I rj ZAEC=ZAEB•J 觥二腿,:.△ ACE ◎△ ABE (ASA )「. AB=AC ,LZCAE=ZBAE•••/ CAE= / CDE ••• AM 是BC 的垂直平分线,二CM=BM , CE=BE CMA= / BMA ,•/ AE=ED , CE 丄AD , • AC=CD,•/ CAD= / CDA ,•••/ BAC=2 / MPC,又I/ BAC=2 / CAD ,•••/ MPC= / CAD , •/ MPC= / CDA , •/ MPF= / CDM ,•/ MPF= / CDM (等角的补角相等),J / DCM+ / CMD+ / CDM=180 ° / F+/ MPF+ / PMF=180 °又•••/ PMF= / BMA= / CMD,•/ MCD= / F.14. 如图,已知△ ABC是等边三角形,点D、E分别在BC、AC边上,且AE=CD , AD与BE相交于点F.(1)线段AD与BE有什么关系?试证明你的结论.(2)求/ BFD的度数.考点::等边三角形的性质;全等三角形的判定与性质.分析:(1)根据等边三角形的性质可知/ BAC= / C=60 ° AB=CA ,结合AE=CD ,可证明△ ABE ◎△ CAD , 从而证得结论;(2)根据/ BFD= / ABE+ / BAD,/ ABE= / CAD,可知/ BFD= / CAD+ / BAD= / BAC=60 °解答:(1)证明:•••△ ABC 为等边三角形,•/ BAC= / C=60 ° AB=CA . 在厶ABE和厶CAD中,F AB=AC-ZBAE=ZC •••△ ABE ◎△CAD • AD=BE .k AE=CD(2 )解:J/ BFD= / ABE+ / BAD ,又•••△ ABE CAD,•/ ABE= / CAD . •/ BFD= / CAD+ / BAD= / BAC=60 °15. 如图,在△ ABC中,AB=BC,/ ABC=90 ° F为AB延长线上一点,点E在BC上,BE=BF,连接AE、EF 和CF,求证:AE=CF .考点:全等三角形的判定与性质.分析:根据已知利用SAS即可判定△ ABE ◎△ CBF,根据全等三角形的对应边相等即可得到AE=CF . 解答:证明:J/ ABC=90 ° •/ ABE= / CBF=90 °又J AB=BC , BE=BF , •△ABE CBF ( SAS). • AE=CF .16.已知:如图,在△ OAB 中,/ AOB=90 ° OA=OB,在△ EOF 中,/ EOF=90 ° OE=OF,连接AE、BF .问线段AE理由:在△ AEO与厶BFO中,••• Rt △ OAB 与Rt △ OEF 等腰直角三角形,二AO=OB , OE=OF,/ AOE=90。
