华一寄宿2017-2018元调模拟试卷
2018年华一寄分班测试卷

二、判断题(打“√”或“×”,并说明理由)(每小题5分,共10分)1.圆锥的体积比它等底等高圆柱体积小23。
()2.在一个数的末尾添上三个0,现数就扩大为原数的1000倍。
()三、计算题(每小题5分,共15分)1.12(2.250.3750.32) 1.2563÷⨯-⨯÷2.129...1212312 (10)+++⨯⨯⨯⨯⨯⨯5.从12、6、4、24、18五个数中取出成倍数关系的一对数,最多可取出____对。
杯子的容量是________升。
4.一个杯子底部直径是高度的一半,装水高度8厘米时占杯内容量的40%,那么这个价________元。
3.每把椅子定价20元,获得的利润是25%,若要使利润达到40%,则每把椅子应定2.一个三角形的三边长分别是5cm ,13cm ,12cm ,则它的面积是________cm²。
元。
1.王阿姨买了一万元的国库券,定期五年,年利率为3.24%,到期可取回________一、填空题(每小题5分,共25分)数学卷(卷面总分:100分时间:60分钟)2018年华一寄分班测试卷3.111...1321353135 (40352018)++++-++-++++-四、解答题(每小题8分,共40分)1.把一串数字按下列规律排列:2,0,1,8,2,0,1,8,2,……,求前2018个数字的和。
2.小芳早上去上学,离家时,墙上挂钟(一圈刻着1至12)分针正对着8,时针也在8附近,小芳每分钟走40米,到学校发现作业本没带,立即返回,每分钟走60米,到家时,看到分针正对着1,时针还在8附近,试求小芳家离学校的距离。
3.车间里有60名男女工人在生产零件。
男工每人完成90件,女工每人完成60件,平均每人完成70件,那么男女工人各有多少?4.暑假里小明一家到印度旅游,当地导游有兄妹俩,小明问导游哥哥:“你有几个兄弟,几个姐妹?”导游哥哥答:“我有几个兄弟,我就有几个姐妹,”小明再问导游妹妹:“你有几个兄弟,几个姐妹?”导游妹妹答:“我的兄弟数是姐妹数的2倍。
2018武汉元调数学试卷及答案(Word精校版)
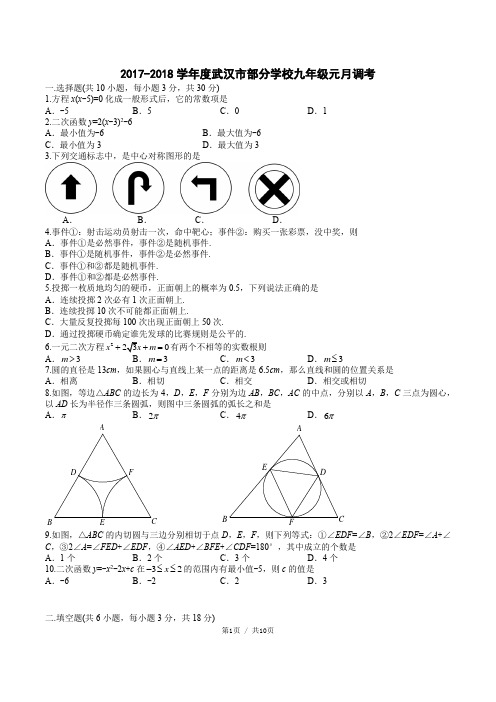
第1页 / 共10页2017-2018学年度武汉市部分学校九年级元月调考一.选择题(共10小题,每小题3分,共30分) 1.方程x (x -5)=0化成一般形式后,它的常数项是A .-5B .5C .0D .12.二次函数y =2(x -3)2-6A .最小值为-6B .最大值为-6C .最小值为3D .最大值为3 3.下列交通标志中,是中心对称图形的是A .B .C .D .4.事件①:射击运动员射击一次,命中靶心;事件②:购买一张彩票,没中奖,则 A .事件①是必然事件,事件②是随机事件. B .事件①是随机事件,事件②是必然事件. C .事件①和②都是随机事件. D .事件①和②都是必然事件.5.投掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确的是 A .连续投掷2次必有1次正面朝上. B .连续投掷10次不可能都正面朝上.C .大量反复投掷每100次出现正面朝上50次.D .通过投掷硬币确定谁先发球的比赛规则是公平的.6.一元二次方程20x m ++=有两个不相等的实数根则A .3m >B .3m =C .3m <D .3m ≤7.圆的直径是13cm ,如果圆心与直线上某一点的距离是6.5cm ,那么直线和圆的位置关系是 A .相离 B .相切 C .相交 D .相交或相切8.如图,等边△ABC 的边长为4,D ,E ,F 分别为边AB ,BC ,AC 的中点,分别以A ,B ,C 三点为圆心,以AD 长为半径作三条圆弧,则图中三条圆弧的弧长之和是A .πB .2πC .4πD .6π9.如图,△ABC 的内切圆与三边分别相切于点D ,E ,F ,则下列等式:①∠EDF =∠B ,②2∠EDF =∠A +∠C ,③2∠A =∠FED +∠EDF ,④∠AED +∠BFE +∠CDF =180°,其中成立的个数是 A .1个 B .2个 C .3个 D .4个 10.二次函数y =-x 2-2x +c 在32x -≤≤的范围内有最小值-5,则c 的值是 A .-6 B .-2 C .2 D .3二.填空题(共6小题,每小题3分,共18分)B第2页 / 共10页11.一元二次方程20x a -=的一个根是2,则a 的值是 .12.把抛物线22y x =先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是 . 13.一个不透明的口袋中有四个完全相同的小球,把它们分别标记为1,2,3,4.随机摸取一个小球然后放回, 再随机摸出一个小球,两次取出的小球标号的和为5的概率是 .14.设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的比,可以增加视觉美感,按此比例,如果雕像的高为2m ,那么上部应设计为多高?设雕像的上部高为x m ,列方程,并化成一般形式为 .15.如图,正六边形ABCDEF 中,P 是边ED 的中点,连接AP ,则AP AB=16.在O 中,AB 所对的圆心角108AOB ∠=︒,点C 为O 上的动点,以AO ,AC 为边构造AODC ,当∠A= °时,线段BD 最长.三.解答题(共8小题,共72分) 17. (本题8分)解方程230x x +-=AA第3页 / 共10页18. (本题8分)如图在O 中,半径OA 与弦BD 垂直,点C 在O 上,∠AOB=80°. (1)若点C 在优弧BD 上,求∠ACD 的大小; (2)若点C 在劣弧BD 上,直接写出∠ACD 的大小.19.(本题8分)甲,乙,丙三个盒子中分别装有除颜色以外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球,乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球. (1)请画树状图,列举所有可能的结果;(2)请直接写出事件“取出至少一个红球”的概率.20. (本题8分)如图,在平面直角坐标系中有点A(-4,0),B(0,3),点分别为C,D.(1)当a=-4时,①在图中画出线段CD,保留作图痕迹;②线段CD向下平移个单位时,四边形ABCD为菱形;(2)当a=时,四边形ABCD为正方形.21. (本题8分)如图,点D在⊙O的直径AB的延长线上,CD切⊙O于点C,AE⊥CD于点E.(1)求证:AC平分∠DAE.(2)若AB=6,BD=2,求CE的长.A第4页 / 共10页22. (本题10分)投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m.设平行于墙的边长为xm.(1)设垂直于墙的一边长为y,请直接写出y与x之间的函数关系式.(2)若菜园面积为384m2,求x的值.(3)求菜园的最大面积.23. (本题10分)如图,点C为线段AB上一点,分别以AB,AC,CB为底作顶角为120°的等腰三角形,顶角顶点分别为D,E,F,(点E,F在AB的同侧,点D在另一侧).(1)如图1,若点C是AB的中点,则∠AED=__________;(2)如图2,若点C不是AB的中点,①求证:△DEF为等边三角形;②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.AA第5页 / 共10页24.(本题12分)已知抛物线22=++与x轴交于A(-1,0),B(3,0)两点,一次函数y=kx+b的图象l经y ax x c过抛物线上的点C(m,n).(1)求抛物线的解析式;(2)若m=3,直线l与抛物线只有一个公共点,求k的值;(3)若k=-2m+2,直线l与抛物线的对称轴相交于点D,点P在对称轴上,当PD=PC时,求点P的坐标.第6页 / 共10页第7页 / 共10页2017-2018学年度武汉市部分学校九年级元月调考解析一.选择题9.如图:①∵∠EOF =2∠EDF ,∠EOF +∠B =180°, ∴2∠EDF +∠B =180°所以①错误②∵∠EOF =2∠EDF ,∠EOF +∠B =180°, ∠A +∠B +∠C =180°,∴2∠EDF =∠A +∠C 所以②正确③∵∠EDF +∠DEF =2x +y +z =90°+x ,∵∠A+∠EOD =180°,∴∠A =180°-2(y +z )=2x , ∴2(∠EDF +∠DEF )-180°=∠A 所以③错误④∠AED +∠BFE +∠CDF =90°-x +90°-y +90°-z =270°-(x +y +z )=270°-90°=180° 所以④正确二.填空题 11. 412. 2287y x x=++ 13.1414. 2-640x x +=15.16.27°16.延长AO 与O 交于点P ,连接DP ,如图,则 O CAO D P ∆∆≌ DP OC ∴=,即点D 的运动轨迹是以点P 为圆心,OC 长 为半径的圆.如图所示,连接BP ,BP 与P 的交点记作'DBD 最大值为'BD ,此时1'272A POD APB ∠=∠=∠=三.解答题17.1x 1x =PD’BOAC B第8页 / 共10页18. (1)∵OA ⊥BD , ∴AB =AD ,∴∠ACD =12∠AOB =40° (2)40°或140°19.(1)由题意可得如下树状图,由图可知共有12种等可能的情况.(2)5620.(1)如图所示 (2)2(3)72-21.(1)证明:连OC∵CD 与⊙O 切于点C , ∴OC ⊥DE ,∠OCD =90°∵AE ⊥DE , ∴∠E =90°,∴∠OCD =∠E =90°,∴OC //AE , ∴∠1=∠2 ∵OC =OA , ∴∠1=∠3, ∴∠2=∠3, ∴AC 平分∠DAE (2)解:作CH ⊥OD∵AB =6, ∴AO =OB =OC =3∵AC 平分∠DAE ,CH ⊥OD ,CE ⊥AE , ∴CE =CH ∵∠OCD =90°, ∴CD∵OCD S ∆=12OC ·CD =12OD ·CH , ∴CH =125, ∴CE =12522. (1)由题意可知: 200x +150⨯2y =10000化简得:210033y x =-+∴y 与x 之间的函数关系式210033y x =-+(024x <≤)(2)210038433x x ⎛⎫-+= ⎪⎝⎭整理得:()22549x -=解得:x 1=18,x 2=32∵024x <≤ ∴x =18即菜园面积为384m 2,x 的值为18. (3)设菜园的面积SS =210033x x ⎛⎫-+ ⎪⎝⎭=()2212502533x --+A第9页 / 共10页∵203-<,开口向下对称轴x =25∴当024x <≤时,y 随x 的增大而增大. ∴当x =24时,S 的最大值为416. 所以,菜园的最大面积为416 m 2 23. (1)90°(2)①证明:延长AE 、BF 交于G ,连DG .易证四边形ADBG 为菱形,△ADG 为等边三角形,四边形EGFC 为平行四边形. 可证∠DAE =∠DGF =60°,AE =CE =GF . 在△ADE 和△GDF 中. DA DG DAE DGF AE GF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△GDF (SAS ) ∴DE =DF ,∠ADE =∠GDF∴∠EDF =∠EDG +∠GDF =∠EDG +∠ADE =∠ADG =60° ∴△EDF 为等边三角形.②EF24.(1)将A (-1,0),B (3,0)代入22y ax x c =++中得:02096a ca c =-+⎧⎨=++⎩解得:a =-1,c =3∴抛物线的解析式为223y x x =-++(2)当m =3时,n =-9+6+3=0, ∴C (3,0), 将点C 代入y =kx +b 中得: 0=3k +b , ∴b =-3k , ∴l 的解析式为y =kx -3k联立:2323y kx ky x x =-⎧⎨=-++⎩得:()22330x k x k +---= ∵l 与抛物线只有一个交点BA第10页 / 共10页∴()()224330k k ∆=----=得:k =-4(3)当k =-2m +2时,y =(-2m +2)x +b 且m ≠1 将C (m ,n )代入y =(-2m +2)x +b 中得: n =(-2m +2)m +b ∵223n m m =-++∴23b m =+,l 的解析式为()2223y m x m =-+++ ∵D 为l 与抛物线对称轴的交点∴1D x =, 当x =1时,225y m m =-+ ∴()21,25D m m -+,()2,23C m m m -++ 设()1,P a , ∵PC =PD ,∴22PC PD =即()()()2222212325m m m a m m a -+-++-=-+-解得:154a =, ∴P 的坐标为(1,154)。
2018年武汉市元调模拟数学卷及答案

2
3
3
2
解得 x= 2 3 42 , ∴M( 2 3 42 ,– 1 ).
2
2
2
②当 D 是 MQ 的中点时,过 M 作 MS∥x 轴交 y 轴于 S,
△QOD≌△MSD,∴OD=DS,∴DS=1,∴yM=﹣2,代入抛物
线解析式得 1 x2﹣ 2 3 x﹣3=﹣2,解得 x= 3 6
3
3
∴OB=1 2 ,喷水最远有1 2 米远.
21. (1)略; (2)作 AH⊥OD 于 H,OG⊥AB 于 G, △AHE≌△ADE,EH=DE=1, ∵OH=HE=1,
∴OD=3, AH = 2 2 ,
OE × AH = AE × OG 得,
OG = 4 2 , 由 AG2 = OA2 - OG2 3
∴M( 3 6 ,–2).
③当 Q 是 MD 的中点时,过 M 作 MK⊥x 轴于 K,△DOQ≌△
MKQ,∴MK=OD=1,∴yM=1,代入抛物线解析式得 1 x2﹣ 2 3
3
3
x﹣3=1 ,解得 x= 3 15 ,∴M( 3 15 ,1)
∴M( 2 3 42 ,– 1 )或( 3 6 ,–2)或( 3 15 ,1).
2
2
(3)分别过 E 作 EK⊥AB,ES⊥AC,垂足分别为 K、S,过 P 作 PT ⊥AB 于 T.易知直线 AD 的解析式是:y=– 3 x–1, 3
联立
y
3 x 1 3
,
y
1 3
x2
23 3
x
3
整理得: 1 x2 3 x 2 0 , 33
2017——2018湖北省武汉市武昌区七校初三上期中考试数学试卷(华一寄宿学校)word版无答案

2017-2018学年度上学期部分学校联合测试数学试卷一、选择题(共10小题,每小题3分,共30分)1.民族图案是数学文化中的一块瑰宝,下列图案中,既不是中心对称图形也不是轴对称图形的是().A .B .C .D .2.二次函数222y x x =-+的顶点坐标是().A .(1,1)B .(2,2)C .(1,2)D .(1,3)3.如图,Rt ABC △中,90C ∠=︒,点D 在边BC 上,BD ,把ABC △绕着点D 逆时针旋转(0180)αα<<度后,点B 恰好落在AC 边上的点B '处,则角α的度数为().A .45︒B .75︒C .135︒D .150︒ 4.用配方法解关于x 的一元二次方程2230x x --=,配方后的方程可以是().A .2(1)4x -=B .2(1)4x +=C .2(1)16x -=D .2(1)16x +=5.已知1是关于x 的一元二次方程2(1)10m x x -++=的一个根,则m 的值是().A .1B .1-C .0D .无法确定6.将点(4,0)A 绕着原点O 顺时针方向旋转60︒角到对应点A ',则点A '的坐标是().A .(4,2)-B .(2,-C .D .2)-7.若二次函数2()1y x m =--,当1x ≤时,y 随x 的增大而减小,则m 的取值范围是().A .1m =B .1m >C .1m ≥D .1m ≤8.如图,AB 是⊙O 的弦,C 是AB 上一点,且2BC AC =,连OC 并延长交⊙O 于点D ,若3OC =,2CD =,则O 到AB 的距离是().A .B .9CD .25-9.如图,已知A 、B 两点的坐标分别为(2,0)、(0,2),⊙C 的圆心坐标为(1,0)-,半径为1,若D 是⊙C 上的一个动点,线段DA 与y 轴交于点E ,则ABE △的面积的最小值是().A .2B .1C .2D .210.二次函数2(0)y ax bx c a =++≠的图象的顶点在第一象限,通过(0,1),(1,0)-,则S a b c =++的值的变化范围是().A .01S <<B .12S <<C .12S <<D .11S -<<二、填空题(共6小题,每小题3分,共18分)11.抛物线22y x =+有最__________点,其坐标是__________.12.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干、小分支的总数为73,则每个支干长出__________个小分支.13.若点P 的坐标为(1,1)x y +-,其关于原点对称的点P '的坐标为(3,5)--,则(,)x y 为__________. 14.关于x 的方程2(5)310a x x ---=有实数根,则a 的取值范围为__________.15.如图,AB 是半⊙O 的直径,AC AD =,2OC =,30CAB ∠=︒,则点O 到CD 的距离OE =__________.16.函数22y x px q =+-的图象与x 轴无交点,则p q +的取值范围是__________.三、解答题(共72分) 17.解方程:2450x x +-=.18.如图,已知等腰ABC △的顶角顶点A 在⊙O 的内部,点B 、C 在圆上,连接OA ,求证:OA BC ⊥.19.二次函数2(0)y ax bx c a =++≠的图象如图所示,根据图象解答下列问题: (1)求函数解析式并直接写出不等式0y >的解集.(2)若方程2ax bx c k ++=有两个不相等的实数根,求k 的取值范围.20.如图,在每个小正方形的边长均为1的方格纸中,有线段AB ,点A 、B 均在小正方形的顶点上. (1)在方格纸中画出以AB 为腰的等腰ABC △,点C 在小正方形的顶点上,且ABC △的面积为6. (2)在方格纸中画出ABC △的中线BD ,并把线段BD 绕点C 逆时针旋转90︒画出旋转后的线段EF (B 与E 对应,D 与F 对应),连接BF ,请直接写出BF 的长__________.21.如图AB 为⊙O 的直径,点D 为AB 下方圆上一点,点C 为ACD 的中点,连接CA 、CD . (1)求证:2ABD BDC ∠=∠.(2)连AD ,过点C 作CE AB ⊥交AB 于H ,交AD 于点E ,若5OH =,24AD =,求线段DE 的长度.22.如图所示,ABCD 是边长为60cm 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD 四个点重合于图中的点P ,正好形成一个长方体形状的包装盒,E 、F 在AB 上是被切去的等腰直角三角形斜边的两个端点,若广告商要求包装盒面积2cm S 最大,试求x 应取何值?设cm AE FB x ==,包装盒侧面积...为2cm S . (1)分析:由正方形硬纸片ABCD 的边长为60cm ,cm AE FB x ==,则EF =__________cm .为更好地寻找题目中等量关系,将剪掉的阴影部分三角形集中,得到边长为EF 的正方形,其面积为__________2cm ;折起的四个角上的四个等腰直角三角形的面积之和为__________2cm . (2)由以上分析:用含x 的代数式表示包装盒的侧面积S 并求出问题的解.23.如图,在等边ABC △中,点D 为边BC 上一动点,以AD 为底在直线AD 左侧作等腰ADE △,且AE DE =,120AED ∠=︒(D 点在运动过程中,点E 始终在ABD △的内部). (1)ADB ∠和BAE ∠的数量关系为__________. (2)如图1所示,判断BDE △的形状并证明.(3)当D 点运动到如图2所示的位置时,延长BE 交AD 于点F ,若2DF AF =,2BF =+等边ABC △的边长为__________.24.在平面直角坐标系中,点O为坐标原点,抛物线23 22y ax ax=-+与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为线段AC的中点.(1)如图1,求抛物线的顶点坐标和解析式.(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ AC⊥于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式.(3)在(2)的条件下,如图3,连接AP,过点C作CE AP⊥于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.。
华一入学试卷

2017 年华一寄入学测试题满分:100 分时间 60 分钟一、计算题(每题 5 分,共 25 分)1234 2341 3412 4123 215421033 6511362 548 361411 3511 4 362 54818634451 3 7 29 37 41 53 29 37 8 36 56 63 72 77 84 88二、填空题(每题 3 分,共 27 分)12341.观察下列数字,并在横线上填入适当的数字:、、、、。
251017x y13072.已知 x,y 满足方程组 xy10则 x,y 的值是。
7y23.一列火车前 3 小时行驶了 360 千米,然后将速度提高了 10%,又行驶了 2 小时,那么火车一共行驶了千米。
1114.一次考试,参加加的学生中有得优,得良,得中,其余的得差,已知参加考试的732学生不超 50 人,那么得差的学生有人。
15.如下图,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成正方形区域域甲,和 L 形区域乙和丙。
已知三块区域甲、乙、丙的周长之比为 4:5:7,并且区域丙的面积 48,则大正方形的面积为。
丙乙甲6.我们规定两人轮流做一个工程是指,第一个人先做一个小时,第二个人做一个小时,然后再由第一个做一个小时,然后又由第二个人做一个小时。
如此反复,做完为止,如果甲、乙轮流做一个工程需要小时,而乙、甲轮流做同样的工程只需要小时,那乙单独做这个工程需要小时。
7. 已知S1,则 S 的整数部分是。
111120002002200120178.有一个四位数满足下列条件:它的各位数字都是奇数,它的各位数字互不相同;它的每个数字都能整除它本身,则满足条件四位数总共有个。
9.如下图,在长为 490 米的环形跑道上,A、B两点之间的跑道长 50 米,甲、乙两人同时从 A、B 两点出发反向奔跑。
两人相遇后,乙立刻转身与甲同向奔跑,同时甲把速度提高了 25%,乙把速度提高了 20%。
2017 华一寄宿学校八(上)物理第一次月考测试题、答题卡

2017 华一寄宿学校八(上)物理第一次月考测试题一、选择题:(每小题2分,共50分) 1、下列单位换算中正确的是( )A, 3.01m=3010mm=301dm B .5.1Km =5.1Km×1000m=5100m C .30min=30÷60h=0.5h D .30μm=3×10-2 mm=3×10-4 dm2、如图3是用厚刻度尺测量木块的长度,其中正确的测量图是( )A B C D3、小明同学用刻度尺先后四次测量一物体长度,各次测量结果分别是 5.43cm 、5.45cm 、5.46cm ,5.83cm 则此物体长度应是( )A .5.44cmB .5.45cmC .5.447cmD .5.54cm4、下列说法正确的是( )A .振动停止则声音停止B .物体振动就一定能听到声音C .多次认真测量一定能避免出现误差D .测量中错误是可以避免的,而误差是不可避免的5、小恒将一端系有乒乓球的细绳栓在横杆上,当鼓槌敲击鼓面时的力度越大时,乒乓球跳动高度越高,该实验中使用的乒乓球目的是( ) A .研究乒乓球的发声是由于乒乓球的跳动产生的 B .研究乒乓球发声的响度与其跳动高度的关系 C .研究乒乓球的跳动高度与敲击鼓面力度大小关系 D .用乒乓球的跳动来显示鼓面振动的幅度6、小明和张伟进行百米赛跑,每次小明都要比张伟提前10m 到达终点,若让小明将起点向后远离原起点10m,张伟仍在起点处与小明同时起跑,按原来的平均速度,则( ) A 、小明先到终点 B 、张伟先到终点C 、两人同时到达终点D 、条件不足,无法判断7、甲同学骑自行车去看望乙同学,得知消息后,乙同学步行去迎 接,接到后同车返回.整个过程他们的位置与时间的关系如右图 所示,据图可知( )A. 两同学在t=10 min 时速度相等B. 相遇前甲的速度是乙的4倍C. 相遇后乙的速度是原来的2倍D. 整个过程甲的平均速度是乙的1.5倍8、关于匀速直线运动的速度公式v=s/t 正确的说法是( ) A.速度v 与路程s 成正比 B.路程s 与速度v 成正比 C.对于匀速直线运动,路程s 与时间t 成正比例 D.速度v 与时间t 反比9、船在静水中行驶的速度为v1,河水的速度为v2(v1>v2),那么以河水为参照物,船( )A .逆水行驶速度为v1-v2,顺水行驶速度为v1+v2B .逆水行驶速度为v1+v2,顺水行驶速度为v1--V2C .逆水行驶速度为vl ,顺水行驶速度为v1D .逆水行驶速度为v1,顺水行驶速度为v1+v210、如图所示声波的波形图,下列说法正确的是( )A .甲、乙的音调和响度相同 B.甲、丙的音调和音色相同 C. 乙、丁的音调和音色相同 D.丙、丁的音色和响度相同10题图 11题图11、 战斗机水平飞行时,飞行员从左侧舷窗看到如图甲所示的“天地分界线”。
华一寄宿分班考试模拟试题5套

华一寄宿分班考试五套模拟试题(一)(1)一、填空题:2.用长短相同的火柴棍摆成5×1997的方格网,每一个小方格的边长为一根火柴棍长(如图),共需用______根火柴棍.4.一块长方形耕地如图所示,已知其中三块小长方形的面积分别是15、16、20亩,则阴影部分的面积是______亩.5.现有大小油桶40个,每个大桶可装油5千克,每个小桶可装油3千克,大桶比小桶共多装油24千克,那么,大油桶_____个,小油桶______个.6.如图,把A,B,C,D,E,F这六个部分用5种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,那么这幅图一共有______种不同的着色方法.7."123456789101112…282930"是一个多位数,从中划去40个数字,使剩下的数字(先后顺序不能变)组成最大的多位数,这个最大的多位数是______.8.一水库存水量一定,河水均匀流入水库内.5台抽水机连续抽10天可以抽干;6台同样的抽水机连续抽8天可以抽干。
若要求4天抽干,需要同样的抽水机______台.9.如图,A、C两地相距3千米,C、B两地相距8千米.甲、乙两人同时从C地出发,甲向A地走,乙向B地走,并且到达这两地又都立即返回.如果乙的速度是甲的速度的2倍,那么当甲到达D地时,还未能与乙相遇,他们相距1千米,这时乙距D地_ _____千米.10.一次足球赛,有A、B、C、D四队参加,每两队都赛一场.按规则,胜一场得2分,平一场得1分,负一场得0分.比赛结果,C队得5分,A队得3分,D队得1分,所有场次共进了9个球,C队进球最多,进了4个球,A队共失了3个球,B队一个球也没进,D队与A队比分是2∶3,则D队与C队的比分是______.二、解答题:1.一个人以相同的速度在小路上散步,从第1棵树走到第13棵树用了18分,如果这个人走了24分,应走到第几棵树?2.在黑板上写出3个整数分别是1,3,5,然后擦去一个换成其它两数之和,这样操作下去,最后能否得到57,64,108?为什么?3.有一根6厘米长的绳子,它的一端固定在长是2厘米、宽是1厘米的长方形的一个顶点A处(如图),让绳子另一端C与边AB在一条线上,然后把它按顺时针方向绕长方形一周,绳子扫过的面积是多少?4.如图,四个圆相互交叉,它们把四个圆面分成13个区域.如果在这些区域上(加点的)分别填上6至18的自然数,然后把每个圆中的数各自分别相加,最后把这四个圆的和相加得总和,那么总和最大可能是多少?华一寄宿分班考试五套模拟试题(一)(2)一、填空题:1.[240-(0.125×76+12.5%×24)×8]÷14=______.2.下面的加法算式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字。
华一寄宿2017-2018年度上学期10月八年级数学试题内容规范标准答案

华一寄宿八年级10月月考测试题一、选择题(本大题共10个小题,每小题3分,共30分)1.一个三角形的三个内角的度数之比为4:5:6,这个三角形一定是( ) 直角三角形等腰三角形锐角三角形钝角三角形2.长为10、7、5、3的四根木条,选其中三根组成三角形,有( )种选法. A.2 B.3 C.4 D.53.具备下列条件的两个三角形,全等的是( )A.两个角分别相等,且有一边相等B.一边相等,且这边上的高也相等C.两边分别相等,且第三边上的中线也相等D.两边且其中一条对应边的对角对应相等4.如图,已知∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是( ) A.BD =CD B.AB =AC C.∠B =∠C D.∠BAD =∠CAD5.直角三角形ABC 中,∠ABC =90°,AB =3,BC =4,AC =5,则△ABC 的三条高之和为( ) A.8.4 B.9.4 C.10.4 D.11.46.AD 是△ABC 中BC 边上的中线,若AB =4,AC =6,则AD 的取值值范围是( ) A.AD >1 B.AD <5 C.1<AD <5 D.2<AD <10第4题AB CD 12第8题ABCD第10题ACD E FG H M N7.若两个三角形的两边和其中一边上的高对应相等,则这两个三角形第三边所对应的角的关系是( ) A.相等 B.互余 C.互补 D.相等或互补8.如图,在Rt △ABC 中,∠C =90°,BD 是∠ABC ∠的平分线,交AC 于点D ,若CD =m ,AB =n ,则△ABD 的面积是( )A.mnB.12mnC.2mnD.13mn9.如图,在甲组图形中,每个图形是由四种简单图形A 、B 、C 、D (不同的线段和三角形)中的某两种图形组成,例如由A 、B 组成的图形记为A ★B ,在乙组图形的(a ),(b ),(c ),(d )四个图中,表示“A ★D ”和“A ★C ”的分别是( )(甲)dcb(乙)A.(a),(b)B.(b),(c)C.(c),(d)D.(b),(d)10.如图,△ABC中,AD平分∠BAC,△ABC的两条高线BE,CF交于点H,CF、BE分别交AD于M、N两点,HG平分∠BHC,下列结论:①∠ABE=∠ACF;②∠HMN=∠HNM;③AD//HG;④∠AMF=∠BAC.其中正确的结论有()A.1个B.2个C.3个D.4个二、填空题(本大题共6个小题,每小题3分,共18分)11.一个三角形的三个外角的度数之比为7:6:5,则这个三角形中相应的三个内角的比等于_____________.12.一个等腰三角形的边长分别是4cm和7cm,则它的周长是____________________.13.如图,∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为_____________.14.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则正方形的面积为______.15.如图在5×5的正方形方格中,有A、B两点,已知方格的边长为2,在网格中找点C,以A、B、C为顶点的三角形的面积为2,则你能找到满足条件的C点共有___________个.16.如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=123°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠DAC的度数为_________度.第13题ACDE F第14题lABCDE F第15题第16题ABD三、解答题(本大题共8个小题,共计72分)17.如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.AB CD432118.已知:AB//ED,∠EAB =∠BDE,AF=CD,EF=BC,求证:∠F=∠C.ABCDE F19.如果一个凸多边形的所有内角从小到大排列起来,恰好依次增加的度数相同,设最小角为100°,最大角为140°,那么这个多边形的边数为多少?20.如图,在∠AOB 的两边OA 、OB 上分别取OM =ON ,OD =OE ,DN 和EM 相交于点C , 求证:点C 在∠AOB 的平分线上.OA BCDEM N21.如图,AD 是△ABC 的中线,CE //AB ,AD 平分∠BAE ,求证:AB =AE +EC .ABCDE22.已知:如图,E 在△ABC 的边AC 上,且∠AEB =∠ABC ,(1)求证:∠ABE =∠C ;(2)若∠BAE 的平分线AF 交BE 于F ,FD //BC 交AC 于D 点,设AB =5,AC =8,求DC 的长.ABCDEF23.已知在△ABC 中,AO ⊥BC 于点O ,BO =CO ,点D 为△ABC 左侧一动点,如图所示,点E 在BD 的延长线上,CD 交AB 于F ,且∠BDC =2∠BAO ,(1)求证:∠ABD =∠ACD ;(2)求证AD 平分∠CDE .F E DABO(3)若在D 点运动的过程中,始终有DC =DA +DB ,在此过程中,∠BAC 的度数否发生变化?如果变化,请说 明理由;如果不变,请求出∠BAC 的度数.F E DABCO24.如图所示,等腰Rt △ABC 中,∠ABC =90°,点A 、B 分别在坐标轴上. (1)若C 点的横坐标为5时,求B 点的坐标;(2)当等腰Rt △ABC 在运动过程中,位置如图所示,若x 轴恰好平分∠BAC ,BC 交x 轴于M ,过C 点作CD ⊥x 轴于D ,求CDAM的值; (3)若A 的坐标为(-4,0),点B 在y 轴正半轴上运动时,分别以OB 、AB 为边在第一、第二象限作等腰直角△OBF 和等腰直角△ABE ,连EF 交y 轴于P 点,问当点B 在y 轴上运动时,下列两个结论:①FB 的长为定值,②EF -EB 的值为定值;有且只有一个结论正确,请选择,并求其值.八年级10月月考数学测试答题卡一、选择题(本大题共10小题,每小题3分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017~2018学年度九年级元调模拟考试数学试卷
姓名: 班级: 分数:
一、选择题(共10小题,每小题3分,共30分)
1.下列图标中是中心对称图形的为( )
A .
B .
C .
D .
2.若1x 、2x 是一元二次方程2x -2x =3的两根,则1x ·2x 的值为( )
A .-2
B . 2
C .-3
D .3
3.在平面直角坐标系中,与点P 关于原点对称的点Q 为(1,-3),则点P 的坐标是( )
A .(1,3)
B .(-1,-3)
C .(1,-3)
D .(-1,3)
4.将抛物线y =2x 向右平移2个单长度得到的抛物线的解析式为( )
A .y =2x -2
B .y =2x +2
C . y =2(2)x -
D .y =2(2)x +
5.下列事件中,是必然事件的是( )
A .经过长期努力学习,你会成为科学家
B .抛出的蓝球会下落
C .打开电视机,正在直播NBA
D D .从一批灯泡中任意拿一个灯泡,能正常发光
6.已知圆中两条平行的弦之间距离为1,其中一弦长为8,若半径为5 则另一弦长为( )
A .6
B .
C .6或
D .以上说法都不对
7.共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆,设该公司第二、三个月投放单车数量的月平均增长率为x ,则所列方程正确的是( )
A .1000(1+x )2=440
B .1000(1+x )2=1000
C .1000(1+2x )=1000+440
D .1000(1+x )2= 1000+440
8.如下图所示是一个滑轮的起重装置,已知滑轮的半径为10cm ,一条半径OA 绕轴心O 按逆时针方向旋转,当重物上升5πcm 时,则半径OA 转过的面积是(假设绳索与滑轮之间没有滑动)( )
A .15πcm 2
B . 20πcm 2
C .25πcm 2
D .30πcm 2
第8题图
则他的投篮命中率为( )
A .45
B .23
C .34
D .不能确定 10.已知非负数a ,b ,c 满足a +b =2,c -3a =4,设S =a 2+b +c 的最大值为m ,最小值为n ,则m -n 的值为( )
A .9
B .8
C .1
D .
103
二、填空题(本大题共6个小题,每小题3分,共18分) 11.某事件经过5000 000 00次试验,出现的频率是0.3,它的概本估计值是 .
12.如图,A 、B 、C 为⊙O 上三点,∠ACB =20°,则∠BAO 的度数为 .
13.某种产品预计两年内成本将下降36%,则年平均下降率为 .
14.已知扇形的圆心角为120°,弧长等于一个半经为5cm 的圆的周长,则扇形的面积为 cm 2.(结果保留π)
15.如图,正六边形ABCDEF 中,若四边形ACDF 的面积是20cm 2,则正六边形ABCDEF 的面积 cm 2.
16.如图,以AB 为边作正方形ABCD ,动点P 、Q 在正方形ABCD 的边上运动,且PQ =8,若点P 从点A 出发,沿A →B →C →D 的线路,向D 点运动,点Q 只能在线段AD 上运动,求点P 从A 到D 的运动过程中,PQ 的中点O 所经过的路径的长为 .
第12题图
第15题图
第16
题图
三、解答题(共8小题,共72分)
17.(本题8分)解方程:2x -2x -15=0
18. (本题8分)如图,△ABC 的三个顶点都在⊙O 上,直径AD =6cm ,∠DAC =2∠B (1)连CO ,证明:△AOC 为等边角形;(2)求AC 的长.
D
19.(本题8分)在一幅长80cm ,宽50cm 的矩形风景画的四周镶一条金色纸边,制成一副矩形挂图,如图所示,如果要使整个挂图的面积是5400cm 2,求出金色纸边的宽度.
20.(本题8分)现有若干完全相同的硬币(硬币的正反面图案不同).按如下方式抛掷硬币:
方式一:从中选取一枚硬币抛掷;方式二:从中选取两校硬币抛掷;方式三:从中选取三枚硬币抛掷.
请你在每一种抛掷方式中,各找出一种随机现象,使得这三种随机现象的概率相等(要求:概率不能为0或1),并说明理由.
21.(本题8分)已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=1
2 OB.
(1)求证:AB是⊙O的切线;(2)若∠ACD=45°,OC=2,求弦CD的长.
D
C
O
22.(本题10分)某市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100,在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销该原料日获利润w(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利润最大?最大获利是多少元?
23.(本题10分)如图1,已知点E为正方形ABCD对角线CA延长线上一点,过E点作EF⊥CB交其延
长线于点F,且EF
=4,AC
(1)如图1,连接BE ,求线段BE 的长;
(2)将等腰Rt △CEF 绕C 点旋转至如图2的位置,连接AE ,M 点为AE 的中点,连接MD 、MF ,求MD 与MF 的关系;
(3)将△CEF 绕C 点旋转一周,请直接写出点M 在这个过程中的运动路径长为 .
图1A D
F E
M
E
F
A B D
C 图2
24.(本题12分)已知抛物线y =(m +1)2+(
12
m -2)x -3,(1)无论m 取何值,抛物线必过第三象限一个定点,则该定点的坐标为 ;(不影响后两问解答) (2)当m =0时,不与坐标轴平行的直线l 1与抛物线有且只有一个交点P (2,a ), 求直线l 1的解析式;
(3)在(2)的条件下,直线y =kx +b 交抛物线于M , N 两点(M 在N 的右侧),PQ //y 轴交MN 于点Q ,若MQ =NQ ,求k 的值
.
图1。
