三种基本逻辑运算
逻辑代数中的三种基本运算
1 1 0 0
+ + B A+ B A + B A+ B A⋅ B ⋅ 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 0 0 0 1 0
相等
相等
五、若干常用公式
(1) AB+ AB = A( B + B) = A +
(2) A+ AB= A(1 + B) = A +
推广
A + A(
)= A
即 ⊙ A⊕ B = A⊙B ⊕ 同理可证 A⊙B = A⊕ B ⊙ ⊕
六、关于异或运算的一些公式 异或 A ⊕ B = A B + AB 同或 A⊙B = AB + A B ⊙ (1) 交换律 (2) 结合律 (3) 分配律 ⊙ A⊕ B = A⊙B ⊕ A⊙B = A⊕ B ⊙ ⊕
(5) 因果互换律
= AB + AC + ABC + ABC = AB+ A + C
推论
AB + A + BCD = AB + A C C
AB + AB = A B + AB
证明: 公式 (5) 证明:
左 = A B ⋅ AB = ( A + B ) ( A + B ) = A ⋅ A + A B + AB + B ⋅ B = A B + AB
曾用符号 A B Y
美国符号 A B A B Y
≥1
Y = A+ B A
B =1 Y = A⊕ B A B
Y
Y
⊕
Y
A B
Y
1.3
逻辑运算

逻辑运算
一、简介
逻辑运算是数字符号化的逻辑推演法,包括联合、相交、相减。
在图形处理操作中引用了这种逻辑运算方法以使简单的基本图形组合产生新的形体,并由二维逻辑运算发展到三维图形的逻辑运算。
由于布尔在符号逻辑运算中的特殊贡献,很多计算机语言中将逻辑运算称为布尔运算,将其结果称为布尔值。
二、基本概念
逻辑运算:在逻辑运算中,有与、或、非三种基本逻辑运算。
表示逻辑运算的方法有多种,如语句描述、逻辑代数式、真值表、卡诺图等。
三、逻辑运算符
在形式逻辑中,逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。
1、逻辑“与”AND:指两个条件同时成立。
如“在家偷玩游戏”与“妈妈回家了”,可以将它们组成“在家偷玩游戏且妈妈回家了”。
2、逻辑“或”OR:指两个条件中的任意一个成立。
如“晚餐吃蛋糕”或“晚餐吃炸鸡”,可以组成“晚餐吃蛋糕或炸鸡,我会很开心”。
3、逻辑“非”NOT:指将原结果做相反的计算。
如条件“飞机飞行”,结果“下飞机”可以组成“飞机不飞行时,才能下飞机”。
四、各种编程语言中的逻辑运算符。
第1章 逻辑代数基础

①代入规则:任何一个含有变量 A 的等式,如果将所有出现 A 的位置都用
同一个逻辑函数代替,则等式仍然成立。这个规则称为代入规则。 例如,已知等式 AB A B ,用函数 Y=AC 代替等式中的 A,
根据代入规则,等式仍然成立,即有:
( AC) B AC B A B C
A
E
B Y
4
第1章 逻辑代数基础---三种基本运算
功能归纳:
真值表:
开关 A 开关 B 断开 断开 闭合 闭合 断开 闭合 断开 闭合
灯Y 灭 灭 灭 亮
A 0 0 1 1
B 0 1 0 1
Y 0 0 0 1
将开关接通记作1,断开记作0;灯亮记作1,灯灭记作0。可以作出如
上表格来描述与逻辑关系,这种把所有可能的条件组合及其对应结果一一列
的逻辑函数, 并记为:
F f ( A, B, C , )
3
第1章 逻辑代数基础---三种基本运算
②三种基本运算
a.与逻辑(与运算)
定义:仅当决定事件(Y)发生的所有条件(A,B,C,…)均满足 时,事件(Y)才能发生。表达式为:
Y=A· C· B· …=ABC…
描述:开关A,B串联控制灯泡Y
法进行描述。每种方法各具特点,可以相互转换。 ①真值表
将输入变量的各种可能取值和相应的函数值排列在一起而组成的表格。
真值表列写方法:每一个变量均有0、1两种取值,n个变量共有2n种不 同的取值,将这2n种不同的取值按顺序(一般按二进制递增规律)排列起
来,同时在相应位置上填入函数的值,便可得到逻辑函数的真值表。
原式左边
AB A C ( A A ) BC
基本逻辑运算

1
1
0
1
1
0
(3) 逻辑符号 国 A 标 B
=1 L
国 外
A B
L *
10
4、同或逻辑
(1) 逻辑式: L=A⊙B (2) 真值表
A 0 0 1 1 B 0 1 0 1 L 1 0 0 1
L AB AB
只有两变量 参与运算
同入出1 异入出0
同或门 表示反相 L
(3) 逻辑符号 国 A 标 B
*
4
2、或逻辑(逻辑加)
(1)定义:在决定事物结果的诸条件中只要任何一个满 足,结果就会发生。 A (2)逻辑式:L= A + B
B + _
(3)真值表
设 开关闭合为 1,断开为 0 灯亮为 1,熄灭为 0
A 0 0 B 0 1 L 0 1
L
当逻辑变量A、B中任何一 个为1时,逻辑函数L等于1。 (低低得低)
只有输入A、B同时为0时,输 出L才为1 有1出0 全0出1
或非门 表示反相 L 表示反相
(3) 逻辑符号 国 A 标 B
1
国 A 外 B
L *
9
3、异或逻辑
(1) 逻辑式: L A B (2) 真值表
A 0 0 B 0 1 L 0 1
L AB AB
只有两变量 参与运算
同入出0 异入出1
分配律
B A.B B.A 0 0 0 1 0 0 0 0 0 1 1 1
*
13
2、常用恒等式
AB AC BC AB AC
含A的 原变量 含A的 反变量 含除A以外的 其余因子
冗余 项
如何证明?
检验等式两边的真值表 是否相等
常用的逻辑运算符及其作用

常用的逻辑运算符及其作用逻辑运算符是用来连接或改变逻辑表达式的运算符,常见的有与、或、非三种逻辑运算符。
在编程中,逻辑运算符经常用于判断条件和控制流程,是程序设计中不可或缺的一部分。
下面将分别介绍这三种常用的逻辑运算符及其作用。
一、与运算符(&&)与运算符用两个“&”表示,表示逻辑与的关系。
当两个操作数都为真(非零)时,结果为真,否则结果为假。
在编程中,与运算符常用于判断条件的复合情况。
例如:假设有一个判断条件为A && B,其中A为真,B为假。
根据与运算符的规则,由于B为假,所以整个判断条件的结果为假。
二、或运算符(||)或运算符用两个“|”表示,表示逻辑或的关系。
当两个操作数中至少一个为真(非零)时,结果为真,否则结果为假。
在编程中,或运算符常用于判断条件的多种情况。
例如:假设有一个判断条件为A || B,其中A为真,B为假。
根据或运算符的规则,由于A为真,所以整个判断条件的结果为真。
三、非运算符(!)非运算符用一个“!”表示,表示逻辑非的关系。
它是一个单目运算符,用于将操作数的逻辑值取反。
当操作数为真(非零)时,结果为假,当操作数为假(零)时,结果为真。
在编程中,非运算符常用于判断条件的取反情况。
例如:假设有一个判断条件为!A,其中A为真。
根据非运算符的规则,由于A为真,所以整个判断条件的结果为假。
通过使用这三种常用的逻辑运算符,我们可以构建复杂的条件判断和控制流程。
在实际的编程中,我们通常会使用表达式来表示条件判断,这些表达式由逻辑运算符连接而成。
除了与、或、非这三种基本的逻辑运算符之外,还有一些扩展的逻辑运算符,如异或(^)、条件运算符(?:)等。
异或运算符表示两个操作数中只有一个为真时,结果为真;条件运算符用于根据条件的真假来选择不同的操作。
逻辑运算符在编程中起到了至关重要的作用,它们可以帮助我们构建复杂的条件判断和控制流程,使程序更加灵活和高效。
与或非三种运算规则符号

与或非三种运算规则符号与、或、非是逻辑运算中常用的三种规则符号,它们能够帮助我们对命题或命题组进行逻辑判断和推理。
以下将详细介绍这三种运算规则符号及其特点和应用。
一、与运算(∧)与运算又称交运算或合取运算,表示同时满足两个命题的关系。
用符号“∧”表示。
对于两个命题p和q,p∧q是一个新的命题,当且仅当p和q都为真时,该命题为真;否则,该命题为假。
与运算具有以下特点:1.结合律:(p∧q)∧r = p∧(q∧r),即与运算满足结合律,不论括号如何分配,最终结果都是相同的。
2.交换律:p∧q = q∧p,即与运算满足交换律,两个命题顺序变化不影响最终结果。
3.吸收律:p∧(p∨q) = p,即与运算满足吸收律,当一个命题与另一个包含它的命题进行与运算时,结果为前者自身。
4.务实律:p∧(q∨r) = (p∧q)∨(p∧r),即与运算满足迪摩根律,可以通过拆分进行更复杂的逻辑运算。
与运算在逻辑学和数学中都有重要的应用。
在逻辑推理中,与运算用于判断多个条件是否同时满足;在数学中,与运算用于集合的交运算,即求两个集合的公共元素。
二、或运算(∨)或运算又称并运算或析取运算,表示至少有一个命题为真的关系。
用符号“∨”表示。
对于两个命题p和q,p∨q是一个新的命题,当且仅当p和q至少有一个为真时,该命题为真;否则,该命题为假。
或运算具有以下特点:1.结合律:(p∨q)∨r = p∨(q∨r),即或运算满足结合律,不论括号如何分配,最终结果都是相同的。
2.交换律:p∨q = q∨p,即或运算满足交换律,两个命题顺序变化不影响最终结果。
3.分配律:p∨(q∧r) = (p∨q)∧(p∨r),即或运算满足分配律,可以通过拆分进行更复杂的逻辑运算。
或运算在逻辑学和数学中都有重要的应用。
在逻辑推理中,或运算经常用于构建假设或条件选择;在数学中,或运算用于集合的并运算,即求两个集合的所有元素。
三、非运算(¬)非运算又称非定或非否运算,表示否定或取反的关系。
逻辑代数基础

式中符号“⊙”表示同或运算。
表2-12 同或逻辑的真值表
图2-8 同或逻辑的逻辑符号
2020/6/27 “相同为1,相异为0”
A BY 0 01 0 10 1 00 1 11
13
复习与思考
▪ 请举出现实生活中与、或、非的事例? ▪ 两个变量的异或运算和同或运算之间是什么关系?
2020/6/27
14
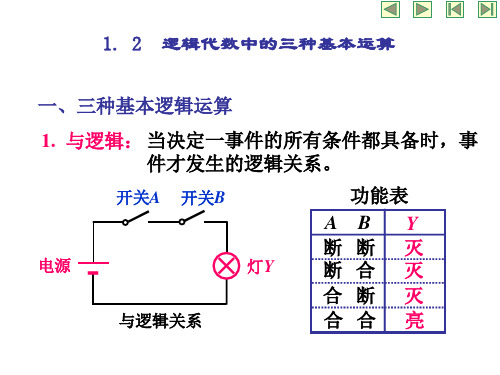
串联开关电路功能表
表1-6 与逻辑的真值表
开关A 开关B 灯Y
A BY
断开 断开 灭
0 00
断开 闭合 闭合 2020/6/27
闭合 断开 闭合
灭 A、B全1, 0 1 0
灭 Y才为1。 1 0 0
亮
1 1 12
逻辑表达式: Y=A ·B=AB 符号“·”读作“与”(或读作“逻辑乘”); 在不致引起混淆的前提下,“·”常被省略。
2.2 逻辑代数中的三种基本运算
逻辑:一定的因果关系。 逻辑代数是描述客观事物逻辑关系的数学方法, 是进行逻辑分析与综合的数学工具。因为它是英国数 学家乔治·布尔(George Boole)于1847年提出的,所以又 称为布尔代数。 逻辑代数有其自身独立的规律和运算法则,不同 于普通代数。 相同点:都用字母A、B、C……表示变量; 2“逻0真20/6辑1和/2”7,变不假“且量同、0”无。点高和大:电“小逻位1”、辑和表正代低示负数电两之变位种分量、不。的有同逻取和的辑值无逻代范、辑数围开状中仅和态的为关:变“等是量0等”和称和。为非1、
符号“ ’ ” 或“—”读作“ 非 ” 。
实现非逻辑的电路称作非门,非逻辑和非门 的逻辑符号如图1-3(b)所示。
逻辑符号中用小圆圈“ 。”表示非运算,符号 中的“1”表示缓冲。
值逻辑运算

值逻辑运算值逻辑运算在数学和计算机科学中是一种非常重要的概念。
它是指通过对一个或多个输入值进行操作,得到一个输出值的过程。
这种逻辑运算在日常生活中也经常被使用,例如在决策、推理和问题求解等方面。
我们来了解一下值逻辑运算的基本概念。
值逻辑运算通常包括与、或、非三种基本运算。
与运算表示只有当所有输入值都为真时,输出值才为真;或运算表示只要有一个输入值为真,输出值就为真;非运算表示将输入值取反,即真变为假,假变为真。
以与运算为例,我们可以通过以下逻辑表达式来进行描述:如果今天是星期六,并且天气晴朗,那么我就去游泳。
在这个例子中,星期六和天气晴朗就是两个输入值,而去游泳就是输出值。
只有当两个输入值都为真时,输出值才为真,否则输出值为假。
这种逻辑运算在日常生活中经常被用来做决策,帮助我们做出正确的选择。
接下来,我们来看一下或运算。
假设我有两个朋友,一个在A城市,一个在B城市。
如果我要去旅行,只要有一个朋友在目的地城市,我就可以选择去那个城市。
这就是或运算的逻辑。
只要有一个输入值为真,输出值就为真。
我们可以通过这种逻辑运算来解决一些选择问题。
我们来了解一下非运算。
非运算是将输入值取反的操作。
例如,如果今天不下雨,那我就出去玩。
在这个例子中,下雨是输入值,出去玩是输出值。
如果下雨为假,即不下雨,那么输出值就为真,我就会出去玩。
非运算在逻辑推理和问题求解中也经常被使用。
除了与、或、非三种基本逻辑运算,还有一些其他的值逻辑运算,例如异或运算、蕴含运算等。
这些逻辑运算在数学和计算机科学中起着重要的作用,帮助我们解决各种复杂的问题。
值逻辑运算在日常生活中也有很多应用。
例如,在购物决策中,我们可以根据商品的价格和质量来做出选择。
只有当价格适中且质量良好时,我们才会购买。
这就是一个与运算的例子。
在投资决策中,我们可以根据市场的情况和投资品种来决定是否投资。
只有当市场好且投资品种可靠时,我们才会进行投资。
这就是一个与运算的例子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L ≥1
.
A
A
≥1
B
B
L
C
C (a)
L (b)
或逻辑运算的基本规则为:
0 + 0 = 0,0 + 1=1,1 + 0= 1,1 + 1=1。
.
1.3.3 逻辑非运算 NOT 非逻辑:
一件事的发生是以其相反的条件为依据的。
电路图
电源
A
灯
L
语句描述
开关A 灯L 断开 亮 闭合 熄灭
表格描述 表达式
AL 01 10
.
电路图
A
B
电源
灯
L
语句描述
开关
A 断开 断开 闭合 闭合
开关
B 断开 闭合 断开 闭合
灯
L 熄灭 熄灭 熄灭 亮
表格描述 表达式
逻辑符号
AB L
00 0 01 0 10 0
L= A ·B A B
11 1
L &
.
A
B
A& B
Y
(a)
Y (b)
与逻辑运算的基本规则为:
0·0=0,0·1=0,1·0=0,1·1=1
1.3 三种基本逻辑运算
逻辑代数 : 按一定的逻辑规律进行运算的代数。用
字母表示变量,但变量取值仅有0、1两种值,0、1不表示数 值的大小,而表示两种对立的逻辑状态。
逻辑代数定义了3中基本逻辑运算:与 、或、非
1.3.1 逻辑与运算 AND 与逻辑:
只有当一件事的几个条件全部具备之后, 这件事才能发生。
• 与、或、非运算的运算规则 • 门符号的识别 • 真值表描述 • 逻辑表达式描述 • 简单的输入输出波形分析
.
.
1.3.2 逻辑或运算 OR 或逻辑:
当一件事的几个条件只要有一个条件满足, 这件事就会发生。
.
电路图 电源
A
B
灯
L
语句描述
开关
A 断开 断开 闭合 闭合
开关
B 断开 闭合 断开 闭合
灯
L 熄灭
亮 亮 亮
表格描述 表达式
逻辑符号
AB L 00 0 01 1 10 1 11 1
L= A +B A B
.
L= A
逻辑符号
L
A
1
1.3.4 基本运算的推广
与非运算
表达式 L= AB
逻辑号
A
L
&
B
或非运算 异或运算
L= A+B
A ≥1 L B
L= A B+A B
.
A =1 L B
基本逻辑运算分析举例 1
A0 B1
0 1 L =AB 0
.
1 A0 B1
0 L =A+B 1
0
1 A0
A
.
应掌握的内容
