唐山市海港高级中学基础测试(四)(三角函数)
三角函数的诱导公式教学设计

1.3三角函数的诱导公式(第1课时)唐山市海港高级中学郭凤禄(一)回顾知识,完成下列各题.1.求点P0 (2,-1)关于原点、x轴、y轴的对称点坐标.2.求点P(x,y)关于原点、x轴、y轴的对称点坐标,总结横坐标之间关系及纵坐标之间关系.3.如图所示,已知点P0(x,y)是角α的终边与单位圆的交点,求角α的正弦、余弦和正切值.4.(1)试着求390°的终边与单位圆交点的坐标?(2)求390°的正弦、余弦和正切值.比较30°、390°的正弦、余弦和正切值,可以得到结论?sin(2kπ+α)=?cos(2kπ+α)=?tan(2kπ+α)=?(二)探索新知,汇报交流探究1:(1)试着求210°的终边与单位圆交点的坐标吗?求210°的正弦、余弦和正切值.(2)试着求240°的正弦、余弦和正切值.探究2:(1)你说说锐角α的终边与π+α的终边与单位圆交点有什么关系?它们的三角函数之间有什么关系?(2)公式中的角α∈R还成立吗?探究3:(1)锐角α的终边与角(-α)的终边与单位圆的交点有什么关系?(2)锐角α的终边与角(π+α)的终边与单位圆的交点有什么关系?(3)它们的三角函数之间有什么关系?(4)公式中的角α∈R还成立吗?探究4:你能说出诱导公式一至四的推导过程吗?你能概括一下公式一、二、三、四的共同特征并归纳记忆方法吗?(三)巩固应用例1 求下列三角函数值:(1)cos225°;(2)sin11π3;(3)sin(-16π3);(4)例2 化简cos(180°+α)·sin(360°+α)cos(-180°-α)·sin(-180°-α).拓展已知cos(75°+α)=13,求cos(105°-α)的值.(四)课堂小结探究5:通过这节课的学习,大家学到了那些公式?我们运用了那些数学思想和方法?(五)作业布置:1.27页练习1、2、3(其中1题直接在书上填空).2.思考题(预习作业).给定一个角α,终边与角α的终边关于直线y=x对称的角与角α有什么关系?它们的三角函数之间有什么关系?能否证明?。
高中数学必修4三角函数综合测试题及答案详解[2]
![高中数学必修4三角函数综合测试题及答案详解[2]](https://img.taocdn.com/s3/m/ad5543c6a5e9856a5712604e.png)
高中数学必修4三角函数综合测试题及答案详解(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学必修4三角函数综合测试题及答案详解(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学必修4三角函数综合测试题及答案详解(word版可编辑修改)的全部内容。
必修4三角函数综合测试题及答案详解一、选择题1.下列说法中,正确的是( )A.第二象限的角是钝角B.第三象限的角必大于第二象限的角C.-831°是第二象限角D.-95°20′,984°40′,264°40′是终边相同的角2.若点(a,9)在函数y=3x的图象上,则tan错误!的值为()A.0 B。
错误! C.1 D。
错误!3.若|cosθ|=cosθ,|tanθ|=-tanθ,则错误!的终边在()A.第一、三象限B.第二、四象限C.第一、三象限或x轴上D.第二、四象限或x轴上4.如果函数f(x)=sin(πx+θ)(0<θ〈2π)的最小正周期是T,且当x=2时取得最大值,那么( )A.T=2,θ=错误! B.T=1,θ=πC.T=2,θ=π D.T=1,θ=错误!5.若sin错误!=-错误!,且π<x〈2π,则x等于()A。
错误!π B.错误!πC。
错误!π D。
错误!π6.已知a是实数,而函数f(x)=1+a sin ax的图象不可能是( )7.将函数y=sin x的图象向左平移φ(0≤φ〈2π)个单位长度后,得到y=sin错误!的图象,则φ=( )A。
错误! B.错误!C.错误!D.错误!8.若tanθ=2,则错误!的值为( )A.0 B.1C.错误!D.错误!9.函数f(x)=错误!的奇偶性是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.既不是奇函数也不是偶函数10.函数f(x)=x-cos x在(0,+∞)内( )A.没有零点B.有且仅有一个零点C.有且仅有两个零点D.有无穷多个零点11.已知A为锐角,lg(1+cos A)=m,lg错误!=n,则lgsin A的值是()A.m+错误!B.m-nC。
河北省唐山市海港高级中学高二上学期第一次月考数学试题
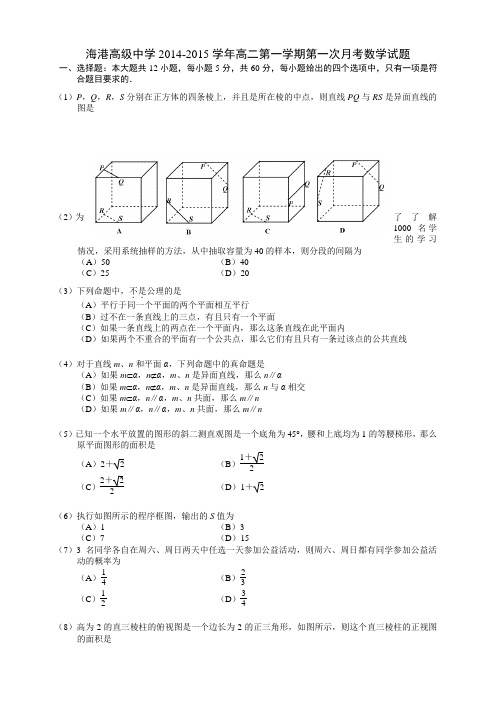
海港高级中学2014-2015学年高二第一学期第一次月考数学试题一、选择题:本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的. (1)P ,Q ,R ,S 分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ 与RS 是异面直线的图是(2)为了了解1000名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为 (A )50 (B )40 (C )25 (D )20 (3)下列命题中,不是..公理的是 (A )平行于同一个平面的两个平面相互平行(B )过不在一条直线上的三点,有且只有一个平面(C )如果一条直线上的两点在一个平面内,那么这条直线在此平面内(D )如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 (4)对于直线m 、n 和平面α,下列命题中的真命题是(A )如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n ∥α(B )如果m ⊂α,n ⊄α,m 、n 是异面直线,那么n 与α相交 (C )如果m ⊂α,n ∥α,m 、n 共面,那么m ∥n (D )如果m ∥α,n ∥α,m 、n 共面,那么m ∥n(5)已知一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是(A )2+ 2 (B )1+22(C )2+22 (D )1+ 2(6)执行如图所示的程序框图,输出的S 值为(A )1 (B )3 (C )7 (D )15(7)3名同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为(A ) 1 4 (B ) 23(C ) 1 2 (D ) 34(8)高为2的直三棱柱的俯视图是一个边长为2的正三角形,如图所示,则这个直三棱柱的正视图的面积是(A )4 (B )2 3 (C )3 (D )2(9)如图,正方体A 1B 1C 1D 1-ABCD 中,AB 的中点为M ,DD 1的中点为N ,则异面直线B 1M 与CN所成的角是(A )30︒ (B )45︒ (C )60︒ (D )90︒(10)设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -1≥0,x -y -1≤0,x -3y +3≥0,则z =x +2y 的最大值为(A )8(B )7 (C )2(D )1(11)已知直线l ⊥平面α,直线m ⊂平面β,有下列命题:①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α⊥β; 其中正确的命题是 (A )①与② (B )③与④ (C )②与④ (D )①与③(12)如图,在棱长为1的正方体A 1B 1C 1D 1-ABCD 中,点E ,F 分别是棱BC ,CC 1的中点,P 是侧面BCC 1B 1内一点,若A 1P //平面AEF ,则线段A 1P 长度的取值范围是(A )[1,52] (B )[324,52](C )[52,2](D )[2,3]二、填空题:本大题共4小题,每小题5分,共20分.(13)如右图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边的长为1,那么这个几何体的表面积为_____________.(14)已知某几何体的三视图如右下图所示,则该几何体的体积为___________.(15)在三棱锥V-ABC中,VB=6,AC=3,P为△VAC的重心,过点P作三棱锥的一个截面,使截面平行于直线VB和AC,则截面的周长为_________.(16)已知正三棱柱内接于一个半径为2的球,则正三棱柱的侧面积取得最大值时,其底面边长为_________.三、解答题:解答应写出文字说明、证明过程或演算步骤.(17)(本小题满分10分)如图,在正方体A1B1C1D1-ABCD中,E,F分别为A1D与D1C的中点.(Ⅰ)证明:EF∥平面ABCD;(Ⅱ)证明:DD1⊥EF.(18)(本小题满分12分)已知等差数列{a n}的前n项和S n满足S3=6,S5=15.(Ⅰ)求{a n}的通项公式;(Ⅱ)求数列{1a2n-1a2n+1}的前n项和.(19)(本小题满分12分)如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△CFD 分别沿DE,EF,DF折起,使A,B,C三点重合于点P.(Ⅰ)求证:平面PDE⊥平面PEF;(Ⅱ)求P到平面DEF的距离.(20)(本小题满分12分)△ABC中,角A,B,C所对的边分别为角a,b,c.已知a=3,cos A=63,B=A+π2.(Ⅰ)求b的值;(Ⅱ)求△ABC的面积.(21)(本小题满分12分)如图,在直三棱柱A 1B 1C 1-ABC 中,∠ACB =90︒,CA =CB =CC 1,M ,P ,N 分别为A 1C 1,A 1C ,BC 的中点.(Ⅰ)证明平面MNP ∥平面ABB 1A 1; (Ⅱ)求A 1C 与平面ABB 1A 1所成的角.(22)(本小题满分12分)如图,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,四边形ABCD 为菱形,E ,F 为PC 的三等分点.(Ⅰ)证明:AC ⊥PB ;(Ⅱ)若PD =3,AD =2,∠BAD =60︒,求二面角P -BC -A 的大小; (Ⅲ)在直线PB 上是否存在一点G ,使平面BDE ∥平面AFG ?说明理由.高二数学10月月考参考答案一、选择题:本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的. (1-5)CCACA (6-10)CDBDB (11-12)DB 二、填空题:本大题共4小题,每小题5分,共20分. (13)3+32(14)3π(15)8(16) 6三、解答题:解答应写出文字说明、证明过程或演算步骤.(17)证明:(Ⅰ)连接AD 1,AC ,∵E 是A 1D 的中点,∴E 也是AD 1的中点,又F 是D 1C 的中点,∴EF 是△ACD 1的中位线, ∴EF ∥AC , ……3分 又EF ⊄平面ABCD ,AC ⊂平面ABCD ,∴EF ∥平面ABCD .……5分 (Ⅱ)∵DD 1⊥平面ABCD ,AC ⊂平面ABCD ,∴DD 1⊥AC ,……8分 又EF ∥AC ,∴DD 1⊥EF . ……10分(18)解:(Ⅰ)设{a n }的公差为d ,则S n =na 1+n (n +1)2d .由已知可得⎩⎨⎧3a 1+3d =6,5a 1+10d =15,解得a 1=1,d =1. ……4分故{a n }的通项公式为a n =n . ……6分(Ⅱ)由(Ⅰ)知1a 2n -1a 2n +1=1( 2n -1)(2n +1)= 1 2(12n -1-12n +1), ……9分从而数列{1a 2n -1a 2n +1}的前n 项和为1 2(1- 1 3+ 1 3- 1 5+…+12n -1-12n +1)=n 2n +1. ……12分 (19)(Ⅰ)证明:由已知四边形ABCD 是正方形,∴∠A =∠B =∠C =90︒,又折叠后A ,B ,C 三点重合于点P , ∴PD ⊥PE ,PD ⊥PF ,PE ⊥PF , 又PE ∩PF =P ,∴PD ⊥平面PEF , ……4分 又PD ⊂平面PDE ,∴平面PDE ⊥平面PEF . ……6分(Ⅱ)解:PD =2,PE =PF =1,EF =2,DE =DF =5, S △DEF =12⨯2⨯5- 1 2= 32,设P 到平面DEF 的距离为d ,由V P -DEF =V D -PEF ,得13⨯ S △DEF ⨯d =13⨯ S △PEF ⨯PD ,……9分∴13⨯ 3 2⨯d =13⨯12⨯1⨯1⨯2,∴d = 23, ∴P 到平面DEF 的距离为 23.……12分 (20)解:(Ⅰ)由题意可知sin A =1-cos 2A =33.……2分 又因为B =A +π 2,所以sin B =sin (A + π2)=cos A =63. ……4分 由正弦定理可知b =a sin Bsin A=32.……6分 (Ⅱ)由B =A + π 2,得cos B =cos (A + π2)=-sin A =-33.……8分由A +B +C =π,得C =π-(A +B ),所以sin C =sin[π-(A +B )]=sin(A +B )=sin A cos B +cos A sin B= 13. ……10分 S △ABC =12ab sin C =12⨯3⨯32⨯13=322. ……12分(21)(Ⅰ)证明:∵M ,P 分别是A 1C 1,A 1C 的中点,∴MP ∥CC 1,又CC 1∥AA 1,∴MP ∥AA 1,又MP ⊄平面ABB 1A 1,AA 1⊂平面ABB 1A 1, ∴MP ∥平面ABB 1A 1, ……4分 同理PN ∥平面ABB 1A 1,MP ∩PN =P ,∴平面MNP ∥平面ABB 1A 1;……6分 (Ⅱ)解:取AB 中点D ,连接CD ,A 1D ,∵AA 1⊥平面ABC ,CD ⊂平面ABC ,∴AA 1⊥CD ,又∵AC =BC ,D 为AB 中点,∴CD ⊥AB ,又AA 1∩AB =A , ∴CD ⊥平面ABB 1A 1,∴∠CA 1D 为A 1C 与平面ABB 1A 1所成的角. ……10分在Rt △CA 1D 中,∠CDA 1=90︒,设CA =1,可得CD =22,A 1C =2, sin ∠CA 1D =CD A 1C =12,∴∠CA 1D =30︒,即A 1C 与平面ABB 1A 1所成的角为30︒.……12分(22)(Ⅰ)证明:∵PD ⊥平面ABCD ,AC ⊂平面ABCD ,∴PD ⊥AC ,又四边形ABCD 为菱形,∴AC ⊥BD ,又PD ∩BD =D ,∴AC ⊥平面PBD ,又PB ⊂平面PBD ,∴AC ⊥PB .……4分 (Ⅱ)解:取BC 中点H ,连接HD ,HC , 由四边形ABCD 为菱形,且∠BAD =60︒,得△BCD 为等边三角形,∴HD ⊥BC ,PH ⊥BC , ∴∠PHD 为二面角P -BC -A 的平面角, ……6分在Rt △PDH 中,∠PDH =90︒,PD =DH =3,∴∠PHD =45︒,即二面角P -BC -A 的大小为45︒.……8分 (Ⅲ)解:当G 为PB 中点时,平面BDE ∥平面AFG .下证: 当G 为PB 中点时,连接FG ,AG ,设AC ∩BD =O ,连接OE ,∵F ,G 分别是PE ,PB 的中点,∴FG ∥EB ,且FG ⊄平面BDE ,EB ⊂平面BDE , ∴FG ∥平面BDE ,同理,AF ∥平面BDE ,又AF ∩FG =F ,∴平面BDE ∥平面AFG , ∴当G 为PB 中点时,平面BDE ∥平面AFG . ……12分。
高中高一数学必修4三角函数练习试卷试题包括答案.docx

高一必修 4 三角函数练习题一、选择题(每题 4 分,计 48 分)1. sin(1560 o) 的值为()A 1B1C3D3 22222.如果 cos(A)1A) =(),那么 sin(22A 1B1C3D3 22223.函数 y cos(32x) 的最小正周期是()5A B 5C2D5524.轴截面是等边三角形的圆锥的侧面展开图的中心角是()A3B2C D4 335.已知 tan100 o k ,则 sin80 o的值等于()AkBkC1k 2 1 k 2 1k 21k2kDk6.若 sin cos 2 ,则tan cot的值为()A1B2C1D27.下列四个函数中,既是(0,) 上的增函数,又是以为周期的偶函数的是()2A y sin xB y |sin x |C y cosxD y | cos x |8.已知 a tan1 , b tan 2, c tan3 ,则()A a b cB c b aC b c aD b a c9.已知 sin(1,则 cos() 的值为())633A1B1C1D1 223310.是第二象限角,且满足cossin2(sincos )2 ,那么 是 ( )象限角22 2 2A 第一B 第二C 第三D 可能是第一,也可能是第三11. 已知 f ( x) 是以 为周期的偶函数,且x [0, ] 时, f ( x) 1 sin x ,则当 x [5,3 ] 时,22f ( x) 等于 ()A 1 sin xB 1 sin xC 1 sin xD 1 sin x12. 函数 f ( x) M sin( x)(0) 在区间 [ a, b] 上是增函数,且 f ( a)M , f (b)M ,则 g( x) M cos( x ) 在 [ a,b] 上()A 是增函数B 是减函数C可以取得最大值 MD可以取得最小值M二、填空题(每题 4 分,计 16 分)13. 函数 ytan( x) 的定义域为 ___________ 。
2023-2024学年河北省唐山市高一上学期数学人教A版-三角函数-专项提升-4-含解析

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年河北省唐山市高一上学期数学人教A版-三角函数-专项提升(4) 姓名:____________ 班级:____________ 学号:____________考试时间:120分钟 满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)1. 已知角 终边上一点P的坐标为 ,则 的值是( )A .B .C .D .±1-1±2-22. 已知角的顶点为坐标原点,始边为x轴的非负半轴,若是角终边上的一点,且 , 则y的值为( )A .B .C .D .013. 已知α∈[ , ],β∈[﹣ ,0],且(α﹣ )3﹣sinα﹣2=0,8β3+2cos 2β+1=0,则sin( +β)的值为( )A .B .C .D .4. 已知角 、 、 分别是 的三个内角,且 ,则 ( )A .B .C .D .15. 一条弦的长等于半径,这条弦所对的圆心角等于( )A .B .C .D .6. 黄金分割比例广泛存在于许多艺术作品中.在三角形中,底与腰之比为黄金分割比的三角形被称作黄金三角形,被认为是最美的三角形,它是两底角为72°的等腰三角形.达·芬奇的名作《蒙娜丽莎》中,在整个画面里形成了一个黄金三角形.如图,在黄金三角形中, , 根据这些信息,可得( )A .B .C .D .7. 的值为 ( )A .B .C .D .- -8. 若f(cosx)=cos2x,f(sin15°)=( )A .B .C .D .9. 已知 , , 则的值为( )A .B .C .D .向左平移个长度单位向右平移个长度单位向左平移个长度单位向右平移个长度单位10. 为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin(2x+)的图象( )A .B .C .D .±44-411. 已知角 的终边经过点 ,且 ,则 ( )A .B .C .D .--12. cos600°的值是( )A .B .C .D .13. 若点 绕坐标原点按逆时针方向旋转30°到达点B,则点B的横坐标是 .14. 若角α的终边经过点P(﹣1,2),则sin2α=15. 已知 , 则 .16. 已知α∈(0,π),tan( )= ,则sin( )= .17. 已知向量 , .(1) 求不等式 的解集;(2) 设 ,若关于x的方程 有且仅有一个实根,求实数m的取值范围.18. 函数f(x)=Asin(ωx﹣ )(A>0,ω>0)的最大值为2,其图象相邻两条对称轴之间的距离为 .(Ⅰ)求函数f(x)的最小正周期及解析式;(Ⅱ)求函数f(x)的单调减区间.19. 函数 (其中 , , )的部分图象如图所示,先把函数 的图象上的各点的横坐标缩短为原来的 (纵坐标不变),把得到的曲线向左平移 个单位长度,再向上平移1个单位,得到函数 的图象.(1) 求函数 图象的对称中心.(2) 当 时,求 的值域.(3) 当 时,方程 有解,求实数m的取值范围.20. 已知函数 .(1) 求 的最小正周期;(2) 求 的单调增区间;(3) 若 ,求 的值.21. 已知 .(1) 若 为锐角,求 ;(2) 求 .答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)18.19.(1)(2)(3)20.(1)(2)(3)21.(1)(2)。
河北省唐山市海港高级中学2014-2015学年高一上学期第一次月考数学试题

海港高级中学2014-2015学年高一第一学期第一次月考数学试题(2014.9.23)(说明:本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),考试时间为120分钟,卷面总分150分,第Ⅰ卷试题答案应涂在答题卡上,考试完毕后,交答题卡和答题卷.) 命题范围:必修1第一章、第二章2.1指数函数第一卷 客观题(满分60分)一、选择题本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x |x 2-2x =0},B ={0,1,2},则A ∩B =( )A .{0}B .{0,1}C .{0,2}D .{0,1,2}2.下列函数中,在区间(0,+∞)上为增函数的是( )A .y =x +1B .y =(x -1)2C .y =2-xD .y =1x3.已知全集U ={0,1,2,3,4}且∁U A ={0,2},则集合A 的非空真子集共有( )A .5个B .6个C .7个D .8个4.给出下列集合A 到集合B 的几种对应:其中,是从A 到B 的映射的是( )A .(1)(2)B .(1)(2)(3)C .(1)(2)(4)D .(1)(2)(3)(4)5.用分数指数幂表示a 3a a ,正确的是( ) A .a 43 B .a 34 C .a 112 D .a- 14 6.已知函数y =f (x +1)定义域是,则y =f (x -1)的定义域是( )A .B .C .D . 7.把函数y =f (x )的图像向左,向下分别平移2个单位,得到y =2x 的图像,则f (x )的解析式是( )A .f (x )=2x +2+2B .f (x )=2x +2-2C .f (x )=2x -2+2D .f (x )=2x -2-28.设f (x )是R 上的偶函数,且当x ∈(0,+∞)时,f (x )=x (1+3x ),则当x ∈(-∞,0)时,f (x )等于( )A .x (1+3x )B .-x (1+3x )C .-x (1-3x )D .x (1-3x )9.已知集合A ={x |2a +1≤x ≤3a -5},B ={x |3≤x ≤22},则能使A ⊆(A ∩B )成立的a 的取值集合为( ).A .B .(-∞,92,+∞) B .C .1,22,3D . B .0,140,120,2内的最大值为g (a ). (Ⅰ)求g (a )的表达式;(Ⅱ)求g (a )的最小值.20. (12分) 根据市场调查,某种新产品投放市场的30天内,每件销售价格P (元)与时间t (天t ∈N *)的关系满足右图,日销售Q (件)与时间t (天)之间的关系是Q =-t +40(t ∈N *).(1)写出该产品每件销售价格P 与时间t 的函数关系;(2)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销量)21.(12分) 设函数f (x )=x 2-2|x |-3.(1)画出y =f (x )的图象,并指出y =f (x )的单调递增区间;(2)判断y =f (x )的奇偶性,并求y =f (x )的值域(3)方程f(x)=k+1有两解,求实数k的取值范围.22.(12分)已知函数f(x)=2x-12x+1.(1)求f(x)的定义域和值域;(2)判断f(x)的奇偶性与单调性;(3)解关于x的不等式f(x2-2x+2) +f(-5) <0.第一次月考数学试题答案一、选择题:1.C ∵A={0,2},∴A∩B={0,2}∩{0,1,2}={0,2}.2.A 由基本初等函数的性质得,选项B中的函数在(0,1)上递减,选项C,D中的函数在(0,+∞)上为减函数,所以排除B,C,D,选A.3.B 依题意,A={1,3,4},∴集合A的非空真子集共有8-2=6个,选择B4.A 根据映射的定义知,(3)中集合A中元素a对应集合B中两个元素x,y,则此对应不是映射;(4)集合A中b在集合B中没有对应元素,且集合A中c对应集合B中两个元素y,z,则此对应不是映射.仅有(1)(2)是映射.5.B a 3a a=12=a12·a16·a112=a34.6.A 由题意知,-2≤x≤3,∴-1≤x+1≤4,∴-1≤x-1≤4,得0≤x≤5,即y=f(x-1)的定义域为.7.C y=2x向上,向右分别平移2个单位得f(x)的图像,所以f(x)=2x-2+2.8.C ∵x∈(0,+∞)时,f(x)=x(1+3x),∴x∈(-∞,0)时,-x∈(0,+∞),f(-x)=-x(1-3x),∵f(x)是R上的偶函数,∴f(x)=-x(1-3x),选择C9.B ∵A⊆(A∩B),∴A⊆B,又A={x|2a+1≤x≤3a-5},当A=φ时,2a+1>3a-5,∴a<6,当A≠φ,∴21352133522a aaa+≤-⎧⎪+≥⎨⎪-≤⎩解得∴6≤a≤9.,∴a的取值集合为(-∞,9-2,22,+∞),∴y=(12)t(x)的增区间为-1,2)∪(2,3解析-1,2)∪(2,3,B=∵f(x)是偶函数,∴f(-x)=f(x),即k(-x)2+(k-1)(-x)+3=kx2+(k-1)x+3,即kx2-(k-1)x+3=kx2+(k-1)x+3,∴-(k-1)=k-1,∴k=1,即f(x)=x2+3.此函数图象为开口向上且以y轴为对称轴的抛物线,所以f(x)的递减区间是(-∞,0f(-2)+2-20,20,aa,20,aa,20,2-4,+ ∞)(8分)(3)由图象(2)分析可知当方程f(x)=k+1有两解时,k+1=-4或k+1>-3,∴k=-5或k>-4(12分)22解析(1)f(x)的定义域是R,令y=2x-12x+1,得2x=-y+1y-1.∵2x>0,∴-y+1y-1>0,解得-1<y<1.∴f(x)的值域为{y|-1<y<1}.(4分)(2)∵f(-x)=2-x-12-x+1=1-2x1+2x=-f(x),∴f(x)是奇函数.∵f (x ) =2x -12x +1=1-22x +1,在R 上任取x 1,x 2,且x 1<x 2,f (x 1)- f (x 2)=∵x 1<x 2,∴12220x x -<,21(21))(21)0x x ++>, f (x 1)< f (x 2), f (x )在R 上是增函数。
河北省唐山市第一中学新高中数学三角函数与解三角形多选题100附答案
河北省唐山市第一中学新高中数学三角函数与解三角形多选题100附答案一、三角函数与解三角形多选题1.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且2a =,sin 2sin B C =,有以下四个命题中正确的是( )A .满足条件的ABC 不可能是直角三角形B .ABC 面积的最大值为43C .当A =2C 时,ABC 的周长为2+D .当A =2C 时,若O 为ABC 的内心,则AOB 【答案】BCD 【分析】对于A ,利用勾股定理的逆定理判断;对于B ,利用圆的方程和三角形的面积公式可得答案; 对于C ,利用正弦定理和三角函数恒等变形公式可得答案对于D ,由已知条件可得ABC 为直角三角形,从而可求出三角形的内切圆半径,从而可得AOB 的面积 【详解】对于A ,因为sin 2sin B C =,所以由正弦定理得,2b c =,若b 是直角三角形的斜边,则有222a c b +=,即2244c c +=,得3c =,所以A 错误; 对于B ,以BC 的中点为坐标原点,BC 所在的直线为x 轴,建立平面直角坐标系,则(1,),(1,0)B C -,设(,)A m n ,因为2b c ==, 化简得22516()39m n ++=,所以点A 在以5,03⎛⎫- ⎪⎝⎭为圆心,43为半径的圆上运动, 所以ABC 面积的最大值为1442233⨯⨯=,所以B 正确; 对于C ,由A =2C ,可得3B C π=-,由sin 2sin B C =得2b c =,由正弦定理得,sin sin b cB C=,即2sin(3)sin c c C C π=-,所以sin32sin C C =,化简得2sin cos 22cos sin 2sin C C C C C +=, 因为sin 0C ≠,所以化简得23cos 4C =,因为2b c =,所以B C >,所以cos C =,则1sin 2C =,所以sin 2sin 1B C ==,所以2B π=,6C π=,3A π=,因为2a =,所以2343,c b ==, 所以ABC 的周长为223+,所以C 正确; 对于D ,由C 可知,ABC 为直角三角形,且2B π=,6C π=,3A π=,2343,c b ==, 所以ABC 的内切圆半径为123433212r ⎛⎫=+-=- ⎪ ⎪⎝⎭, 所以AOB 的面积为1123331122333cr ⎛⎫-=⨯⨯-= ⎪ ⎪⎝⎭所以D 正确, 故选:BCD 【点睛】此题考查三角形的正弦定理和面积公式的运用,考查三角函数的恒等变换,考查转化能力和计算能力,属于难题.2.如图,ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若a b =,且()3cos cos 2sin a C c A b B +=,D 是ABC 外一点,1DC =,3DA =,则下列说法正确的是( )A .ABC 是等边三角形B .若23AC =A ,B ,C ,D 四点共圆 C .四边形ABCD 533 D .四边形ABCD 533 【答案】AC 【分析】利用三角函数恒等变换化简已知等式可求sin B ,再利用a b =,可知ABC 为等边三角形,从而判断A ;利用四点A ,B ,C ,D 共圆,四边形对角互补,从而判断B ;设AC x =,0x >,在ADC 中,由余弦定理可得2106cos x D =-,利用三角形的面积公式,三角函数恒等变换的,可求ABCD S 四边形,利用正弦函数的性质,求出最值,判断CD .【详解】由正弦定理2sin ,2sin ,2sin a R A b R B c R C ===,(sin cos sin cos )2sin sin A C C A B B +=⋅,2sin ,sin B B =∴=, a b =,B 是等腰ABC 的底角,(0,)2B π∴∈,,3B ABC π∴=∴△是等边三角形,A 正确;B 不正确:若,,,A BCD 四点共圆,则四边形对角互补, 由A 正确知21,cos 32D D π∠==-,但由于1,3,DC DA AC ===22211cos 232DC DA AC D DA DC +-===-≠-⋅⋅,∴B 不正确. C 正确,D 不正确:设D θ∠=,则2222cos 106cos AC DC DA DC DA θθ=+-⋅⋅=-,(106cos )ABC S θθ∴=-=△, 3sin 2ADC S θ=△,3sin cos 222ABCADCABCD S S Sθθ∴=+=-+四边形,13(sin cos 2θθ=⋅-+,3sin()3πθ=-+(0,),sin()(3πθπθ∈∴-∈,3ABCD S <≤+四边形,∴C 正确,D 不正确; 故选:AC.. 【点睛】本题主要考查正弦定理,余弦定理,三角函数恒等变换,正弦函数的图象和性质在解三角形中的综合应用,考查计算能力和转化思想,属于中档题.3.已知函数()()sin f x x ωϕ=+(其中,0>ω,||2ϕπ<),08f π⎛⎫-= ⎪⎝⎭,3()8f x f π⎛⎫≤ ⎪⎝⎭恒成立,且()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调,则下列说法正确的是( )A .存在ϕ,使得()f x 是偶函数B .3(0)4f f π⎛⎫=⎪⎝⎭C .ω是奇数D .ω的最大值为3【答案】BCD 【分析】 根据3()8f x f π⎛⎫≤⎪⎝⎭得到21k ω=+,根据单调区间得到3ω≤,得到1ω=或3ω=,故CD 正确,代入验证知()f x 不可能为偶函数,A 错误,计算得到B 正确,得到答案. 【详解】08f π⎛⎫-= ⎪⎝⎭,3()8f x f π⎛⎫≤ ⎪⎝⎭,则3188242k T πππ⎛⎫⎛⎫--==+ ⎪ ⎪⎝⎭⎝⎭,k ∈N , 故221T k π=+,21k ω=+,k ∈N , 08f π⎛⎫-= ⎪⎝⎭,则()s n 08i f x πωϕ⎛⎫=+= ⎪⎭-⎝,故8k πωϕπ+=-,8k ϕπωπ=+,k Z ∈,当,1224x ππ⎛⎫∈-⎪⎝⎭时,,246x k k ωπωπωϕππ⎛⎫+∈++ ⎪⎝⎭,k Z ∈,()f x 在区间,1224ππ⎛⎫-⎪⎝⎭上单调,故241282T πππ⎛⎫--=≤ ⎪⎝⎭,故4T π≥,即8ω≤,0243ωππ<≤,故62ωππ≤,故3ω≤,综上所述:1ω=或3ω=,故CD 正确;1ω=或3ω=,故8k ϕππ=+或38k ϕππ=+,k Z ∈,()f x 不可能为偶函数,A 错误;当1ω=时,(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭,33sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故3(0)4f f π⎛⎫= ⎪⎝⎭;当3ω=时,3(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭, 393sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故3(0)4f f π⎛⎫= ⎪⎝⎭, 综上所述:3(0)4f f π⎛⎫= ⎪⎝⎭,B 正确;故选:BCD. 【点睛】本题考查了三角函数的性质和参数的计算,难度较大,意在考查学生的计算能力和综合应用能力.4.设函数()sin 6f x M x πω⎛⎫=+ ⎪⎝⎭(0,0)M ω>>的周期是π,则下列叙述正确的有( )A .()f x 的图象过点10,2⎛⎫ ⎪⎝⎭B .()f x 的最大值为MC .()f x 在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递减D .5,012π⎛⎫⎪⎝⎭是()f x 的一个对称中心 【答案】BCD 【分析】已知只有周期的条件,只能求出ω,其中M 未知;A 选项代值判定;B 选项由解析式可知;C 选项由()f x 的单调递减区间在32,2,22k k k Z ππππ⎛⎫++∈ ⎪⎝⎭上化简可得;D 选项由()f x 的对称中心为(),0,k k Z π∈化简可得. 【详解】 由题可知2T ππω==,解得2ω=,即()sin 26f x M x π⎛⎫=+ ⎪⎝⎭当0x =时,()0sin 20sin 662Mf M M ππ⎛⎫=⨯+== ⎪⎝⎭,故选项A 错误; 因为()sin 26f x M x π⎛⎫=+⎪⎝⎭,所以最大值为M ,故选项B 正确; 由解析式可知()f x 在3222,262k x k k Z πππππ+≤+≤+∈ 即2,63x k k ππππ⎡⎤∈++⎢⎥⎣⎦上单调递减,当0k =时,选项C 正确; 由解析式可知()f x 的对称中心的横坐标满足26x k ππ+=,即212k x ππ=-当1k =时,512x π=,对称中心为5,012π⎛⎫⎪⎝⎭,故选项D 正确. 故选:BCD 【点睛】本题考查()()sin f x A x =+ωϕ型三角函数的性质,其中涉及最值、对称轴、对称中心,属于较难题.5.在ABC 中,a ,b ,c 分别为A ∠,B ,C ∠的对边,下列叙述正确的是( ) A .若sin sin a bB A=,则ABC 为等腰三角形 B .若cos cos a bB A=,则ABC 为等腰三角形 C .若tan A tan tan 0B C ++<,则ABC 为钝角三角形 D .若sin cos a b C c B =+,则4C π∠=【答案】ACD 【分析】多项选择题,一个一个选项验证:对于A :利用正弦定理判断sin sin A B =,在三角形中只能A=B ,即可判断; 对于B :∵由正弦定理得 sin 2sin 2A B =,可以判断∴ABC 为等腰三角形或直角三角形;对于C :利用三角函数化简得tan A tan tan B C ++sin sin sin =cos cos cos A B CA B C,利用sin 0,sin 0,sin 0,A B C >>>判断cos cos cos A B C 、、必有一个小于0,即可判断; 对于D :利用正弦定理判断得cos sin C C =求出角C . 【详解】对于A :∵由正弦定理得:sin sin a bA B=,而sin sin a b B A =,∴sin sin A B =, ∵A+B+C=π,∴只能A=B ,即ABC 为等腰三角形,故A 正确;对于B :∵由正弦定理得:sin sin a bA B=, ∴若cos cos a bB A=可化为sin cos sin cos A A B B =,即sin 2sin 2A B =, ∴22A B =或22A B π+=∴ABC 为等腰三角形或直角三角形,故B 错误; 对于C :∵A+B+C=π,∴()()()()sin sin sin cos cos cos A B C C A B C C ππ+=-=+=-=,,∴tan A tan tan B C ++sin sin sin =cos cos cos A B CA B C++ sin cos sin cos sin =cos cos cos A B B A CA B C ++sin sin =cos cos cos C CA B C+11=sin cos cos cos C A B C ⎛⎫+ ⎪⎝⎭cos cos cos =sin cos cos cos C A B C A B C +⎛⎫ ⎪⎝⎭sin sin sin =cos cos cos A B CA B C.∵tan A tan tan 0B C ++<而sin 0,sin 0,sin 0,A B C >>> ∴cos cos cos A B C 、、必有一个小于0,∴ABC 为钝角三角形. 故C 正确;对于D :∵sin cos a b C c B =+,∴由正弦定理得:sin sin sin sin cos A B A C B =+, 即sin cos sin cos sin sin sin cos B C C B B C C B +=+ ∴cos sin C C = ∵()0,C π∈∴4C π.故D 正确. 故选:ACD 【点睛】在解三角形中,选择用正弦定理或余弦定理,可以从两方面思考: (1)从题目给出的条件,边角关系来选择; (2)从式子结构来选择.6.已知函数()()cos 2f x A x b ϕ=++(0A >,0ϕπ<<)的部分图像如图所示,则( )A .2A =B .点7,112π⎛⎫⎪⎝⎭是()f x 图像的一个对称中心 C .6π=ϕ D .直线3x π=是()f x 图像的一条对称轴【答案】ABD 【分析】由图知函数最大值为3,最小值为1-,且函数图像与y 轴的交点为()0,2,进而待定系数得()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,再整体换元讨论B,D 选项即可.【详解】因为0A >,所以31A b A b +=⎧⎨-+=-⎩,解得21A b =⎧⎨=⎩,故A 正确;()02cos 12f ϕ=+=,则1cos 2ϕ=.又0ϕπ<<,所以3πϕ=,故C 错误;()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,令23x k ππ+=,k ∈Z ,解得62πk πx =-+,k ∈Z , 所以()f x 图像的对称轴方程为62πk πx =-+, 令1k =,则3x π=,D 正确;令232x k πππ+=+,k ∈Z ,解得122k x ππ=+,k ∈Z , 令1k =,则712x π=且7112f π⎛⎫= ⎪⎝⎭,故B 正确. 故选:ABD【点睛】本题考查三角函数图像求解析式,三角函数的对称轴,对称中心等,考查运算求解能力,是中档题.解题的过程中,需要注意形如()()sin 0y A x B A ωϕ=++>,()()cos 0y A x B A ωϕ=++>,max min ,y A B y A B =+=-+,ϕ的求解通常采用待定系数法求解.7.函数()sin 24f x x π⎛⎫=+⎪⎝⎭,则( ) A .函数()y f x =的图象可由函数sin 2y x =的图象向右平移4π个单位得到 B .函数()y f x =的图象关于直线8x π=轴对称C .函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称D .函数2()y x f x =+在08π⎛⎫ ⎪⎝⎭,上为增函数 【答案】BCD 【分析】对四个选项,一一验证:对于选项A ,利用三角函数相位变化即可;对于选项B ,利用正弦函数的对称轴经过最高(低)点判断; 对于选项C ,利用正弦函数的对称中心直接判断; 对于选项D ,利用复合函数的单调性“同增异减”判断; 【详解】由题意,对于选项A ,函数sin 2y x =的图象向右平移4π个单位可得到()sin 2sin 2cos 242f x x x x ππ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭,所以选项A 错误;对于选项B ,sin 21884f πππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,取到了最大值,所以函数()y f x =的图象关于直线8x π=轴对称,所以选项B 正确;对于选项C ,08f π⎛⎫-= ⎪⎝⎭,所以函数()y f x =的图象关于点,08π⎛⎫- ⎪⎝⎭中心对称,所以选项C 正确;对于选项D ,函数2yx 在08π⎛⎫ ⎪⎝⎭,上为增函数,08x π⎛⎫∈ ⎪⎝⎭,时,2442x πππ⎛⎫+∈ ⎪⎝⎭,,单调递增,所以函数2()y x f x =+在08π⎛⎫ ⎪⎝⎭,上为增函数,所以选项D 正确. 故选:BCD. 【点睛】(1)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题;(2)求单调区间,最后的结论务必写成区间形式,不能写成集合或不等式.8.已知函数()2sin()05,||2f x x πωϕωϕ⎛⎫=+<<< ⎪⎝⎭,且对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,3y f x π⎛⎫=+⎪⎝⎭为奇函数,则下列说法正确的是( ) A .函数()f x 的图象关于原点对称 B .函数()f x 的最小正周期为π C .函数()f x 的图象关于直线2x π=对称D .函数()f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z 【答案】BD 【分析】由()12f x f π⎛⎫≤ ⎪⎝⎭恒成立可得212f π⎛⎫=± ⎪⎝⎭,即()122k k ωππϕπ+=+∈Z ,由3y f x π⎛⎫=+ ⎪⎝⎭为奇函数可得()3k k ωπϕπ''+=∈Z ,即可求出2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,再根据正弦函数的性质分别判断即可. 【详解】因为对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,所以2sin 21212f πωπϕ⎛⎫⎛⎫=+=± ⎪⎪⎝⎭⎝⎭, 即sin 112ωπϕ⎛⎫+=±⎪⎝⎭,得()122k k ωππϕπ+=+∈Z ①. 2sin 2sin 333f x x x ππωπωϕωϕ⎡⎤⎛⎫⎛⎫⎛⎫+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,因为3y f x π⎛⎫=+ ⎪⎝⎭为奇函数,所以()3k k ωπϕπ''+=∈Z ②.由①②可得()(),3122k k k k ωπωπππ''-=--∈Z ,即()(42,)k k k k ω''=--∈Z .又05ω<<,所以1k k '-=,2ω=,则(2,)33k k k k ππϕππ=+=-'∈'Z ,得3πϕ=, 所以2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭, 由于(0)30f =≠,故()f x 的图象不关于原点对称,所以A 不正确;()f x 的最小正周期22T ππ==,所以B 正确; 2sin 22sin 2sin 3222333f ππππππ⎛⎫⎛⎫⎛⎫=⨯+=+=-=-≠± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以C 不正确; 令222232k x k πππππ-≤+≤+,k ∈Z ,得51212k x k ππππ-≤≤+,k ∈Z , 故函数() f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ,所以D 正确. 故选:BD.【点睛】 关键点睛:本题考查正弦型函数的性质,解题的关键是:(1)根据“对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立”得到“212f π⎛⎫=± ⎪⎝⎭”;(2)得到“2sin 33f x x πωπωϕ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭”后,能根据“3y f x π⎛⎫=+ ⎪⎝⎭为奇函数”得到“()3k k ωπϕπ''+=∈Z ”.9.函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图象如图所示,则下列结论正确的是( )A .1()2sin 36f x x π⎛⎫=- ⎪⎝⎭ B .若把()f x 的横坐标缩短为原来的23倍,纵坐标不变,得到的函数在[],ππ-上是增函数C .若把函数()f x 的图像向左平移2π个单位,则所得函数是奇函数 D .函数()y f x =的图象关于直线4x π=-对称 【答案】ACD【分析】根据函数的图象求出函数的解析式,得选项A 正确; 求出213263x πππ--得到函数在[],ππ-上不是增函数,得选项B 错误; 求出图象变换后的解析式得到选项C 正确; 求出函数的对称轴方程,得到选项D 正确.【详解】A, 如图所示:1732422T πππ=-=, 6T π∴=,∴2163πωπ==, (2)2f π=,∴2(2)2sin()23f ππϕ=+=,即2sin()13πϕ+=, ∴22()32k k Z ππϕπ+=+∈, ∴2()6k k Z πϕπ=-∈,||ϕπ<, ∴6πϕ=-, ∴1()2sin()36f x x π=-,故选项A 正确; B, 把()y f x =的横坐标缩短为原来的23倍,纵坐标不变,得到的函数12sin()26y x π=-, [x π∈-,]π,∴213263x πππ--, ∴12sin()26y x π=-在[π-,]π上不单调递增,故选项B 错误;C, 把()y f x =的图象向左平移2π个单位,则所得函数12sin[()]2sin 3223x y x ππ=-+=,是奇函数,故选项C 正确;D, 设1,,32,362x k k Z x k πππππ-=+∈∴=+当24k x π=-⇒=-,所以函数()y f x =的图象关于直线4x π=-对称,故选项D 正确.故选:ACD【点睛】方法点睛:求三角函数的解析式,一般利用待定系数法,一般先设出三角函数的解析式sin()y A wx k ,再求待定系数,,,A w k ,最值确定函数的,A k ,周期确定函数的w ,非平衡位置的点确定函数的φ.10.设M 、N 是函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象与直线2y =的交点,若M 、N 两点距离的最小值为6,1,22P ⎛⎫- ⎪⎝⎭是该函数图象上的一个点,则下列说法正确的是( )A .该函数图象的一个对称中心是()7,0B .该函数图象的对称轴方程是132x k =-+,Z k ∈ C .()f x 在71,23⎡⎤--⎢⎥⎣⎦上单调递增 D .()2cos 36x f x ππ⎛⎫=+⎪⎝⎭ 【答案】ABD【分析】 根据函数()f x 的基本性质求出函数()f x 的解析式,可判断D 选项的正误,利用余弦型函数的对称性可判断AB 选项的正误,利用余弦型函数的单调性可判断C 选项的正误.【详解】因为M 、N 是函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象与直线2y =的交点,若M 、N 两点距离的最小值为6,则函数()f x 的最小正周期为6T =,23T ππω∴==, 所以,()2sin 3x f x πϕ⎛⎫=+ ⎪⎝⎭, 将点P 的坐标代入函数()f x 的解析式,可得12sin 226f πϕ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭,则sin 16πϕ⎛⎫-= ⎪⎝⎭.0ϕπ<<,5666πππϕ∴-<-<,则62ππϕ-=,23πϕ∴=, ()22sin 2sin 2cos 3336236f x x x x πππππππ⎛⎫⎛⎫⎛⎫∴=+=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,D 选项正确; 对于A 选项,()7572cos 2cos 0362f πππ⎛⎫=+==⎪⎝⎭,A 选项正确; 对于B 选项,由()36x k k Z πππ+=∈,解得()132x k k Z =-+∈, 所以,函数()f x 的图象的对称轴方程是132x k =-+,k Z ∈,B 选项正确; 对于C 选项,当71,23x ⎡⎤∈--⎢⎥⎣⎦时,3618x ππππ-≤+≤, 所以,函数()f x 在区间71,23⎡⎤--⎢⎥⎣⎦上不单调,C 选项错误. 故选:ABD.【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+或()cos y A x ωϕ=+形式,再求()sin y A ωx φ=+或()cos y A x ωϕ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =或cos y x =的相应单调区间内即可,注意要先把ω化为正数.。
河北省唐山市海港高中高三数学上学期10月月考试卷 理(含解析)
河北省唐山市海港高中2015届高三上学期10月月考数学试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.下列结论正确的有( )①集合A={1,2},集合B={x|x是4的因数},A与B是同一个集合;②集合{y|y=2x2﹣3}与集合{(x,y)|y=2x2﹣3}是同一个集合;③由1,,,|﹣|,0.5这些数组成的集合有5个元素;④集合{(x,y)|xy≤0,x、y∈R}是指第二和第四象限内的点集.A.0个B.1个C.2个D.3个考点:命题的真假判断与应用.专题:集合.分析:①整数的因数是指能被整除的整数,②两集合相等是指两集合中元素完全相同,③集合中元素必需满足互异性,④当x=0,或y=0时也适合不等式xy≤0.解答:解:①B={x|x是4的因数}={﹣4,﹣2,﹣1,1,2,4},所以A≠B,所以①错误;②集合{y|y=2x2﹣3}={y|y≥﹣3}是数集,{(x,y)|y=2x2﹣3}表示曲线y=2x2﹣3上的点,是一个点集,所以两个集合不是同一个集合,所以②错误;③∵=,|﹣|=0.5,∴由1,,,|﹣|,0.5这些数组成的集合有3个元素,所以③错误;④当x=0或y=0也满足xy≤0,所以集合{(x,y)|xy≤0,x、y∈R}是指第二和第四象限内或坐标轴上的点集.所以④错误.故选择:A.点评:本题考查了,集合的有关性质,如集合中元素的互异性,集合的代表元,集合相等,这些都是集合中常考的知识点.属于基础题.2.已知i是虚数单位,a∈R,则“a=1”是“(a+i)2=2i”的( )A.充分必要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:由(a+i)2=2i化为a2﹣1+(2a﹣2)i=0,可得,解得a=1.即可判断出.解答:解:由(a+i)2=2i化为a2﹣1+(2a﹣2)i=0,∴,解得a=1.∴“a=1”是“(a+i)2=2i”的充要条件.故选:A.点评:本题考查了复数的运算法则、复数相等、充要条件的判定方法,属于基础题.3.设命题p:函数y=在定义域上为减函数;命题q:∃a,b∈(0,+∞),当a+b=1时,+=3,以下说法正确的是( )A.p∨q为真B.p∧q为真C.p真q假D.p,q均假考点:复合命题的真假.专题:简易逻辑.分析:根据反比例函数的单调性知,它在定义域上没有单调性,所以命题p是假命题;根据a+b=1得b=1﹣a,带入,看能否解出a,经计算解不出a,所以命题q是假命题,即p,q均假,所以D是正确的.解答:解:函数y=在(﹣∞,0),(0,+∞)上是减函数,在定义域{x|x≠0}上不具有单调性,∴命题p是假命题;由a+b=1得b=1﹣a,带入并整理得:3a2﹣3a+1=0,∴△=9﹣12<0,∴该方程无解,即不存在a,b∈(0,+∞),当a+b=1时,,∴命题q是假命题;∴p,q均价,∴p∨q为假,p∧q为假;故选D.点评:考查反比例函数的单调性,定义域,一元二次方程的解和判别式△的关系.4.阅读程序框图,运行相应的程序,则输出i的值为( )A.3 B.4 C. 5 D.6考点:程序框图.专题:算法和程序框图.分析:通过程序框图的要求,写出前四次循环的结果得到输出的值.解答:解:该程序框图是循环结构经第一次循环得到i=1,a=2;经第二次循环得到i=2,a=5;经第三次循环得到i=3,a=16;经第四次循环得到i=4,a=65满足判断框的条件,执行是,输出4故选B点评:本题考查解决程序框图中的循环结构时,常采用写出前几次循环结果,找规律.5.已知双曲线(a>0)的离心率为2,则实数a=( )A.2 B.C.D.1考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:由双曲线方程找出a,b,c,代入离心率,从而求出a.解答:解:由题意,e===2,解得,a=1.故选D.点评:本题考查了双曲线的定义,属于基础题.6.设,则a,b,c的大小关系是( ) A.a>c>b B.a>b>c C.c>a>b D.b>c>a考点:幂函数图象及其与指数的关系.分析:根据幂函数与指数函数的单调性直接可以判断出来.解答:解:∵在x>0时是增函数∴a>c又∵在x>0时是减函数,所以c>b故答案选A点评:本题主要考查幂函数与指数的关系.要充分利用函数图象、函数的单调性来解决问题.7.规定a⊗b=+2a+b,a、b∈R+,若1⊗k=4,则函数f(x)=k⊗x的值域( ) A.(2,+∞)B.(1,+∞)C.[,+∞)D.[,+∞)考点:函数的值域.专题:函数的性质及应用.分析:由规定的运算法则知,先求出k的值,再根据法则得到f(x),根据函数的单调性,求出值域.解答:解:∵a⊗b=+2a+b,a、b∈R+,∴1⊗k=+2+k=4,解得k=1,∴k⊗x=1⊗x=+2+x,∴f(x)=x++2,∴函数f(x)在(0,+∞)为增函数,∴x++2>2,故函数f(x)的值域为(2,+∞)故选:A.点评:本题考查了新定义下的求函数的值域问题,解题时要严格按照规定的定义进行运算,是基本题.8.要得到函数y=sin(2x﹣)的图象,只要将函数y=cos2x的图象( ) A.向左平移单位B.向右平移单位C.向左平移单位D.向右平移单位考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:由条件利用诱导公式,以及函数y=Asin(ωx+φ)的图象变换规律,可得结论.解答:解:∵y=sin(2x﹣)=cos(﹣2x+)=cos(2x﹣)=cos[2(x﹣)] ∴故将y=cos2x的图象右左平移个单位,可得函数y=sin(2x﹣)的图象,故选:D.点评:本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基本知识的考查.9.已知定义在R上的偶函数f(x)在[0,+∞)上是增函数,且f(ax+1)≤f(x﹣2)对任意都成立,则实数a的取值范围为( )A.[﹣2,0] B.[﹣3,﹣1] C.[﹣5,1] D.[﹣2,1)考点:奇偶性与单调性的综合.专题:计算题.分析:由已知中定义在R上的偶函数f(x)在[0,+∞)上是增函数,根据偶函数单调性的性质,我们可得f(x)在(﹣∞,0)上是减函数,进而可将f(ax+1)≤f(x﹣2)对任意都成立,转化为当时,﹣2≤ax≤0恒成立,解不等式即可得到答案.解答:解:∵偶函数f(x)在[0,+∞)上是增函数,则f(x)在(﹣∞,0)上是减函数,则f(x﹣2)在区间[,1]上的最小值为f(﹣1)=f(1)若f(ax+1)≤f(x﹣2)对任意都成立,当时,﹣1≤ax+1≤1,即﹣2≤ax≤0恒成立则﹣2≤a≤0故选A点评:本题考查的知识点是奇偶性与单调性的综合,其中根据已知条件及偶函数在对称区间上单调性相反,得到函数的单调性是解答本题的关键.10.已知锐角A是△ABC的一个内角,a,b,c是三角形中各角的对应边,若sin2A﹣cos2A=,则下列各式正确的是( )A.b+c=2a B.b+c<2a C.b+c≤2a D.b+c≥2a考点:基本不等式在最值问题中的应用;余弦定理.专题:解三角形;不等式的解法及应用.分析:已知等式左边变形后利用二倍角的余弦函数公式化简,求出cos2A的值,由A为锐角求出A的度数,利用余弦定理列出关系式,把cosA的值代入并利用基本不等式得出关系式,即可做出判断.解答:解:由sin2A﹣cos2A=,得cos2A=﹣,又A为锐角,∴0<2A<π,∴2A=,即A=,由余弦定理有a2=b2+c2﹣bc=(b+c)2﹣3bc≥(b+c)2﹣(b+c)2=,即4a2≥(b+c)2,解得:2a≥b+c,故选:C.点评:此题考查了余弦定理,以及基本不等式的运用,熟练掌握余弦定理是解本题的关键.11.下列四个图中,函数y=的图象可能是( )A.B.C.D.考点:函数的图象.专题:函数的性质及应用.分析:根据四个选择项判断函数值的符号即可选择正确选项.解答:解:当x>0时,y>0,排除A、B两项;当﹣2<x<﹣1时,y>0,排除D项.故选:C.点评:本题考查函数的性质与识图能力,属中档题,一般根据四个选择项来判断对应的函数性质,即可排除三个不符的选项.12.已知函数f(x)=,函数g(x)=asin(x)﹣2a+2(a>0),若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( ) A.[﹣,1] B.[,] C.[,] D.[,2]考点:分段函数的应用.专题:计算题;函数的性质及应用.分析:根据x的范围确定函数f(x)的值域和g(x)的值域,进而根据f(x1)=g(x2)成立,推断出[0,1]∩[2﹣2a,2﹣]≠∅,先看当二者的交集为空集时刻求得a的范围,进而可求得当集合的交集非空时a的范围.解答:解:当x∈[0,]时,y=﹣x,值域是[0,];x∈(,1]时,y=,y′=>0恒成立,故为增函数,值域为(,1].则x∈[0,1]时,f(x)的值域为[0,1],当x∈[0,1]时,g(x)=asin(x)﹣2a+2(a>0),为增函数,值域是[2﹣2a,2﹣],∵存在x1、x2∈[0,1]使得f(x1)=g(x2)成立,∴[0,1]∩[2﹣2a,2﹣]≠∅,若[0,1]∩[2﹣2a,2﹣]=∅,则2﹣2a>1或2﹣<0,即a<,或a>.∴a的取值范围是[,].故选:B.点评:本题主要考查了三角函数的最值,函数的值域问题,不等式的应用.解题的关键是通过看两函数值域之间的关系来确定a的范围.二、填空题(本大题共4小题,每小题5分,共20分,把答案填写在答题纸的相应位置上)13.已知sinacosα=且α∈(0,),则cosα﹣sinα=.考点:二倍角的正弦.专题:三角函数的求值.分析:由α∈(0,),可得cosα>sinα.可得cosα﹣sinα==,即可得出.解答:解:∵α∈(0,),∴cosα>sinα.∴cosα﹣sinα===.故答案为:.点评:本题考查了三角函数的单调性、同角三角函数基本关系式,考查了推理能力,属于基础题.14.函数y=的定义域为{ {x|x,或x≥1}.考点:函数的定义域及其求法.专题:函数的性质及应用.分析:根据函数f(x)的解析式,列出使解析式有意义的不等式组,从而求出f(x)的定义域.解答:解:要使函数有意义,x需满足:,可得 x,或x≥1,故答案为:{ {x|x,或x≥1},点评:本题考查函数定义域的求解,属基础题,要求:开偶次方根被开方数要大于等于零;对数的真数大于零.注意定义域的表示形式.15.设α=cos420°,函数f(x)=,则f()+f(log2)的值等于8.考点:分段函数的应用;对数的运算性质.专题:计算题;函数的性质及应用;三角函数的求值.分析:运用诱导公式求出a的值,再由对数的运算性质和对数恒等式a logaN=N,即可求出结果.解答:解:∵a=cos420°=cos60°=,∴f(x)=,∴f()==2,f()=()log2=2log26=6,∴f()+f(log2)=2+6=8.故答案为:8.点评:本题考查三角函数的求值,考查分段函数及应用,对数的运算和对数恒等式的运用,属于基础题.16.如图,正方体ABCD﹣A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是②③④⑤.(填上所有正确命题的序号)①A1C⊥平面B1CF;②在平面A1B1C1D1内总存在与平面B1EF平行的直线;③△B1EF在侧面BCC1B1上的正投影是面积为定值的三角形;④当E,F为中点时,平面B1EF截该正方体所得的截面图形是五边形;⑤当E,F为中点时,平面B1EF与棱AD交于点P,则AP=.考点:空间中直线与直线之间的位置关系;棱柱的结构特征.专题:空间位置关系与距离.分析:由正方体的结构特征,对所给的几个命题用线面,面面之间的位置关系直接判断正误即可得到答案.解答:解:对于①,A1C⊥平面B1EF,不一定成立,因为A1C⊥平面AC1D,而两个平面面B1EF与面AC1D不一定平行.故①错误;对于②,在平面A1B1C1D1内总存在与平面B1EF平行的直线,此两平面相交,一个面内平行于两个平面的交线一定平行于另一个平面,故②正确;对于③,△B1EF在侧面BCC1B1上的正投影是面积为定值的三角形,此是一个正确的结论,因为其投影三角形的一边是棱BB1,而E点在面上的投影到此棱BB1的距离是定值,故③正确;对于④当E,F为中点时,平面B1EF截该正方体所得的截面图形是五边形B1QEPF,故④正确;对于⑤由面面平行的性质定理可得EQ∥B1F,故D1Q=,B1Q∥PF,故AP=,故⑤正确.故正确的命题有:②③④⑤.故答案为:②③④⑤.点评:本题考点是棱柱的结构特征,考查对正方体的几何特征的了解,以及线面垂直,线面平行等位置关系的判定,涉及到的知识点较多,综合性强.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.如图,点A是单位圆与x轴正半轴的交点,点B(﹣,).(Ⅰ)若∠AOB=α,求sin2α的值;(Ⅱ)设点P为单位圆上的动点,点Q满足=+,∠AOP=2θ(≤θ≤),f(θ)=•,求f(θ)的取值范围.考点:三角函数中的恒等变换应用;任意角的三角函数的定义.专题:三角函数的图像与性质.分析:(Ⅰ)直接结合三角函数的定义求解sinα,cosα的值,然后,根据二倍角公式进行求值;(Ⅱ)首先,求解f(θ)=,然后,根据≤θ≤,确定f(θ)的取值范围.解答:解:(Ⅰ),sin2α=2sinα•cosα=.∴sin2α的值﹣;(Ⅱ)∵P(cos2θ,sin2θ),A(1,0),∴,∴=,∵,∴,,∴,∴f(θ)的取值范围.点评:本题考查三角函数的定义、二倍角公式、两角差的正弦公式等三角函数的知识,考查了运算求解能力、化归与转化思想.18.直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.(Ⅰ)求证:AC⊥B1C;(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;(Ⅲ)当时,求二面角B﹣CD﹣B1的余弦值.考点:用空间向量求平面间的夹角;直线与平面平行的判定;直线与平面垂直的性质.专题:计算题.分析:(I)要证明线与线垂直,根据所给的直三棱柱的侧棱与底面垂直和根据三条边长得到的勾股定理,得到线面垂直,进而得到线线垂直.(II)要证明线面平行,根据线面平行的判定定理,首先证明线与线平行,要写清楚两条线段的位置,得到结论.(III)以C为原点建立空间直角坐标系C﹣xyz,写出要用的点的坐标,构造向量,根据线段的比值,得到向量的坐标,设出法向量,求出法向量,根据向量所成的角做出二面角.解答:证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,所以AC2+BC2=AB2,所以AC⊥BC.因为直三棱柱ABC﹣A1B1C1,所以CC1⊥AC.因为BC∩AC=C,所以AC⊥平面BB1C1C.所以AC⊥B1C.(Ⅱ)证明:连接BC1,交B1C于E,DE.因为直三棱柱ABC﹣A1B1C1,D是AB中点,所以侧面BB1C1C为矩形,DE为△ABC1的中位线,所以DE∥AC1.因为DE⊂平面B1CD,AC1⊄平面B1CD,所以AC1∥平面B1CD.(Ⅲ)解:由(Ⅰ)知AC⊥BC,所以如图,以C为原点建立空间直角坐标系C﹣xyz.则B(3,0,0),A(0,4,0),A1(0,0,c),B1(3,0,4).设D(a,b,0)(a>0,b>0),因为点D在线段AB上,且,即.所以a=2,,.所以,,.平面BCD的法向量为.设平面B1CD的法向量为,由,,得,所以,y=2,.设二面角B﹣CD﹣B1的大小为θ,所以.所以二面角B﹣CD﹣B1的余弦值为.点评:本题考查空间中直线与平面之间的平行和垂直关系,用空间向量求解两个平面的夹角,本题解题的关键是建立坐标系,把理论的推导转化成数字的运算.19.已知定义在(0,+∞)上函数f(x)对任意正数m,n都有f(mn)=f(m)+f(n)﹣,当x>4时,f(x)>,且f()=0.(1)求f(2)的值;(2)解关于x的不等式f(x)+f(x+3)>2.考点:数列的求和.专题:函数的性质及应用.分析:(1)由已知得f(1)=f(1)+f(1)﹣,解得f(1)=,从而f(2×)=f(2)+f()﹣,由此能求出f(2)=1.(2)任取x1,x2∈(0,+∞),且x1<x2,则f(x2)﹣f(x1)=f()﹣=f()﹣=,由此能求出关于x的不等式f(x)+f(x+3)>2的解.解答:解:(1)∵定义在(0,+∞)上函数f(x),对任意正数m,n都有f(mn)=f(m)+f(n)﹣,∴f(1)=f(1)+f(1)﹣,∴f(1)=,∴f(2×)=f(2)+f()﹣,∵f()=0,∴f(2)=1.(2)任取x1,x2∈(0,+∞),且x1<x2,则f(x2)﹣f(x1)=f()﹣=f()﹣=,∵f()=f()+f()﹣,且时,f(x)>,∴,∴,解得x∈(1,+∞).点评:本题考查函数值的求法,考查不等式的解法,是中档题,解题时要认真审题,注意函数性质的合理运用.20.已知椭圆C:=1(a>b>0)的短半轴长为l,动点M(2,t)(t>0)在直线x=(c为半焦距)上.(Ⅰ)求椭圆的标准方程;(Ⅱ)求以OM为直径且被直线3x﹣4y﹣5=0截得的弦长为2的圆的方程;(Ⅲ)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:空间位置关系与距离.分析:(Ⅰ)由点M(2,t)在直线x=上,得,由此能求出椭圆方程.(Ⅱ)以OM为直径的圆的方程为(x﹣1)2+(y﹣)2=.由此利用点到直线的距离公式能求出圆的方程.(Ⅲ)由平几知|ON|2=|OK||OM|,直线OM:y=,直线FN:y=﹣,由,得.由此能证明线段ON的长为定值.解答:(本小题满分12分)(Ⅰ)解:由点M(2,t)在直线x=上,得,故,∴c=1.从而a=.…所以椭圆方程为.…(Ⅱ)解:以OM为直径的圆的方程为x(x﹣2)+y(y﹣t)=0.即(x﹣1)2+(y﹣)2=.其圆心为(1,),半径t=.…因为以OM为直径的圆被直线3x﹣4y﹣5=0截得的弦长为2,所以圆心到直线3x﹣4y﹣5=0的距离d==.所以,解得t=4.所求圆的方程为(x﹣1)2+(y﹣2)2=5.…(Ⅲ)证明:由平几知:|ON|2=|OK||OM|,(K为垂足)直线OM:y=,直线FN:y=﹣,由,得.∴|ON|2==(1+)••2=2.所以线段ON的长为定值.…点评:本题考查椭圆的标准方程和圆的方程的求法,考查线段ON的长为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.21.已知函数f(x)=alnx﹣ax﹣3(a∈R).(Ⅰ)求函数f(x)的单调区间;(Ⅱ)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数在区间(t,3)上总不是单调函数,求m的取值范围;(Ⅲ)求证:.考点:利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.专题:压轴题.分析:利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),对于本题的(1)在求单调区间时要注意函数的定义域以及对参数a的讨论情况;(2)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f'(2)=1,可求a 值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知:,于是可求m的范围.(3)是近年来2015届高考考查的热点问题,即与函数结合证明不等式问题,常用的解题思路是利用前面的结论构造函数,利用函数的单调性,对于函数取单调区间上的正整数自变量n有某些结论成立,进而解答出这类不等式问题的解.解答:解:(Ⅰ)当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);当a<0时,f(x)的单调增区间为[1,+∞),减区间为(0,1];当a=0时,f(x)不是单调函数(Ⅱ)得a=﹣2,f(x)=﹣2lnx+2x﹣3∴,∴g'(x)=3x2+(m+4)x﹣2∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=﹣2∴由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,所以有:,∴(Ⅲ)令a=﹣1此时f(x)=﹣lnx+x﹣3,所以f(1)=﹣2,由(Ⅰ)知f(x)=﹣lnx+x﹣3在(1,+∞)上单调递增,∴当x∈(1,+∞)时f(x)>f(1),即﹣lnx+x﹣1>0,∴lnx<x﹣1对一切x∈(1,+∞)成立,∵n≥2,n∈N*,则有0<lnn<n﹣1,∴∴点评:本题考查利用函数的导数来求函数的单调区间,已知函数曲线上一点求曲线的切线方程即对函数导数的几何意义的考查,考查求导公式的掌握情况.含参数的数学问题的处理,构造函数求解证明不等式问题.四、选修题:请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.22.如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC 的平分线分别交BC和圆O于点D、E,若PA=2PB=10.(1)求证:AC=2AB;(2)求AD•DE的值.考点:相似三角形的判定.专题:推理和证明.分析:(1)通过证明△ABP∽△CAP,然后证明AC=2AB;(2)利用切割线定理以及相交弦定理直接求AD•DE的值.解答:解:(1)∵PA是圆O的切线∴∠PAB=∠ACB又∠P是公共角∴△ABP∽△CAP…∴∴AC=2AB…(2)由切割线定理得:PA2=PB•PC∴PC=20又PB=5∴BC=15…又∵AD是∠BAC的平分线∴∴CD=2DB∴CD=10,DB=5…又由相交弦定理得:AD•DE=CD•DB=50…点评:本题主要考查与圆有关的比例线段、相似三角形的判定及切线性质的应用.属于基础题.23.已知直线l:(t为参数,α为l的倾斜角),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C为:ρ2﹣6ρcosθ+5=0.(1)若直线l与曲线C相切,求α的值;(2)设曲线C上任意一点的直角坐标为(x,y),求x+y的取值范围.考点:简单曲线的极坐标方程;参数方程化成普通方程.专题:坐标系和参数方程.分析:(1)求出圆的直角坐标方程,直线的直角坐标方程,利用直线l与曲线C相切,列出关系式,即可求α的值;(2)曲线C上任意一点的直角坐标为(x,y),通过圆的参数方程,得到x+y的表达式,利用三角函数化简,即可求解取值范围.解答:解:(1)曲线C的直角坐标方程为x2+y2﹣6x+5=0即(x﹣3)2+y2=4曲线C为圆心为(3,0),半径为2的圆.直线l的方程为:xsinα﹣ycosα+sinα=0…∵直线l与曲线C相切∴即…∵α∈[0,π)∴α=…(2)设x=3+2cosθ,y=2sinθ则x+y=3+2cosθ+2sinθ=…∴x+y的取值范围是.…点评:本题考查直线与圆的参数方程以及极坐标方程的应用,直线与圆的位置关系,三角函数的化简求值,考查计算能力.24.已知正实数a、b满足:a2+b2=2.(1)求的最小值m;(2)设函数f(x)=|x﹣t|+|x+|(t≠0),对于(1)中求得的m,是否存在实数x,使得f(x)=成立,说明理由.考点:基本不等式.专题:不等式的解法及应用.分析:(1)利用基本不等式的性质即可得出;(2)利用绝对值形式的三角不等式的性质即可得出.解答:解:(1)∵2=a2+b2≥2ab,即,∴.又∴≥2,当且仅当a=b时取等号.∴m=2.(2)函数f(x)=|x﹣t|+|x+|≥≥2=1,∴满足条件的实数x不存在.点评:本题考查了基本不等式的性质、绝对值形式的三角不等式的性质,考查了计算能力,属于基础题.。
河北省唐山市海港高级中学高三上学期10月月考数学(理)试题 Word版含答案
海港高级中学2015届高三上学期10月月考数学(理)试题(满分150分 考试时间120分钟)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.,若{0}M N ⋂=错误!③由1,5个元素; A .0 D .3个2. 已知i 是虚数单位,a R ∈,则“1a =”是“2()2a i i +=”的( ) A. 充分不必要条件 B. 充分必要条件C. 必要不充分条件D. 既不充分也不必要条件3.命题:q ,(0,)a b ∃∈+∞,当1a b +=时 ) A.p ∨q 为真 C.p 真q 假D.p ,q均假4. 阅读右边的程序框图,运行相应的程序,则输出i 的值为 A .3 B .4 C .5 D .65. 2,则实数=a ( ) D. 16.,则a ,b ,c 的大小关系是()AC .b a c >>D .a c b >>7.,若14k ⊗=,则函数()f xk x =⊗的值域()A.(2,)+∞ B .[2,)+∞ C D8的图象,只要将函数cos 2y x =的图象( )A. C.第4题图9.已知定义的R 上的偶函数()f x 在),0[+∞上是增函数,不等式)2()1(-≤+x f ax f 恒成立,则实数a 的取值范围是B .[]2,0- C.[]5,1-- D.[]2,1- 是ABC ∆的一个内角,,,a b c 是三角形中各角的对应边,若( )B. 2b c a +< C. 2b c a +≤ D. 2b c a +≥ 11.下列四个图中,( )成立,则实数a 的取值范围是( )D. 第Ⅱ卷(非选择题 共90分)13. 14.15.于 .16. 如图,正方体1111ABCD A B C D -的棱长为1,,E F 分别为棱1DD ,AB 上的点.下列说法正确的是__________.(填上所有正确命题的序号)①1A C ⊥平面1B EF ;②在平面1111A B C D 内总存在与平面1B EF 平行的直线;③1B EF △在侧面11BCC B 上的正投影是面积为定值的三角形; ④当,E F 为中点时,平面1B EF 截该正方体所得的截面图形是五边形;第16题图⑤当,E F 为中点时,平面1B EF 与棱AD 交于点P ,则三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 点Q 满足,OQ OA OP =+OB OQ =⋅,求(f θ.18.(本小题满分12分)直三棱柱111ABC A B C -中,5,4,3,AB AC BC === 14AA =,点D 在AB 上.(Ⅰ)若D是AB 中点,求证:1//AC 平面1B CD ; (Ⅱ),求二面角1B CD B --的余弦值.的短半轴长为1,动点(2,)M t (0)t >在直线(c 为半焦距)上.(Ⅱ)求以OM 为直径且被直线3450x y --=截得的弦长为2的圆的方程; (Ⅲ)设F 是椭圆的右焦点,过点F 作OM 的垂线与以OM 为直径的圆交于点N , 求证:线段ON 的长为定值,并求出这个定值.21.((Ⅰ)(Ⅱ)处的切线的倾斜角为45,对于任意的[1,2]t ∈,,求m 的取值范围; (Ⅲ)求证:.AC DBC 1 A 1B 1请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分. 22.(本小题满分10分)选修4—1:几何证明选讲如图,ABC ∆内接于直径为BC 的圆O ,过点A 作圆O 的切线交CB 的延长线于点P ,BAC ∠的平分线分别交BC 和圆O 于点E D 、,若102==PB PA . (1)求证:AB AC 2=;(2)求DE AD ⋅的值.23.(本小题满分10分)选修4-4:坐标系与参数方程 已知直线l :⎩⎨⎧=+-=ααsin cos 1t y t x (t 为参数,α为l 的倾斜角),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 为:05cos 62=+-θρρ.(1)若直线l 与曲线C 相切,求α的值;(2)设曲线C 上任意一点的直角坐标为),(y x ,求y x +的取值范围.24.(本小题满分10分)选修4-5:不等式选讲 已知正实数b a 、满足:ab b a 222=+. (1)求ba 11+的最小值m ; (2)设函数)0(|1|||)(≠++-=t tx t x x f ,对于(1)中求得的m ,是否存在实数x ,使得2)(mx f =成立,说明理由. 高三数学试题(理科)答案一、选择题ABDBD AADBC CB 13.2214. 1{|,1}2x x x ≤-≥或 15. 8 16. ②③④⑤17解 (Ⅰ)由三角函数定义可知31sin ,cos 22y x r r αα====-, 所以313sin 22sin cos 2()222ααα==⨯⨯-=-,即求……………………………5分(Ⅱ)由三角函数定义知(cos 2,sin 2)P θθ,所以(1cos 2,sin 2),OQ OA OP θθ=+=+所以131()(1cos 2)sin 2sin(2)2262f OB OQ πθθθθ=⋅=-++=--, 又因62ππθ≤≤,故52666πππθ≤-≤,即1sin(2)126πθ≤-≤,于是10()2f θ≤≤,所以()f θ的取值范围是1[0,]2.……………………………………12分18.【解】(Ⅰ)连接1BC 交1B C 于点E ,连接DE , 因为直三棱柱中侧面11BCC B 为矩形,所以 E 为1BC 的中点,又D 是AB 中点,于是1//DE AC ,且DE ⊂面1B CD ,1AC ⊄面1B CD ,PA BC D E22题O A C DBC 11B 1E所以1//AC 平面1B CD ;…………………………6分(Ⅱ)由5,4,3,AB AC BC ===知90ACB ∠=,即AC CB ⊥, 又直三棱柱中1AA ⊥面ABC ,于是以C 为原点建立空间 直角坐标系C xyz -如右图所示,于是1(3,0,0),(3,0,4)B B ,又13BD AB =,由平面几何易知4(2,,0)3D ,显然平面BCD 的一个法向量为1(0,0,1)=n , 又设平面1B CD 的一个法向量为2(,,)x y z =n ,则由212(3,0,4),4(2,,0),3CB CD ⎧⊥=⎪⎨⊥=⎪⎩n n ,得340,4203x x y +=⎧⎪⎨+=⎪⎩, 解得4,23x y =-=,取1z =,则24(,2,1)3=-n ,设二面角1B CD B --的平面角为θ,则1212||3361|cos |||||6161θ⋅===⨯n n n n ,又由图知θ为锐角, 所以其余弦值为36161.…………………………………………………………………12分 19.(1)21)1()1()1(-+=f f f ,所以21)1(=f 21)21()2()212(-+=⨯f f f 解得1)2(=f ………4分(2)任取()+∞∈,0,21x x ,且12x x <, 则1)41()4(21)414(21)()()(12121212-+=-⋅=-=-f x x f x x f x x f x f x f ………6分 因为2121)21()21()41(-=-+=f f f ,且4412>x x时23)(>x f所以2131()()1022f x f x ->--=所以)(x f 在()+∞,0上是增函数……9分因为2321)2()2()4(=-+=f f f 所以221)3()3()(2>++=++x x f x f x f 即)4(23)3(2f x x f =>+ 所以⎪⎩⎪⎨⎧>+>+>430302x x x x ,解得()+∞∈,1x ……12分20.(本小题满分12分)Ⅰ)由点(2,)M t 在直线2a x c =上,得22a c=, 故212c c+=, ∴1c =. 从而2a =. ……………2分 所以椭圆方程为2212x y +=. ……………4分 (Ⅱ)以OM 为直径的圆的方程为(2)()0x x y y t -+-=.即222(1)()124t t x y -+-=+. 其圆心为(1,)2t,半径214t r =+.…………6分 yx z A CD B C 1 AB 1方法二:设00(,)N x y ,则00(1,),(2,),(2,),(,FN x y OM t MN x y t ON x y =-==--=0,2(FN OM x ⊥∴-又,(MN ON x x ⊥∴ON x =ln 134n n⨯⨯<ln 123(1),2n n n ⨯⨯<⨯⨯⨯⨯-≥,所以()ln 3(1)2ln 1,1f x x x f x x x =-+->=-⇔<->………………………………11分2,3,4,,n 得3,,ln n n <ln 123(1),2n n n ⨯⨯<⨯⨯⨯⨯-≥ln 1n n⨯⨯<13分(26分8分2分5分9分10分。
2023-2024学年河北省唐山市高一上学期数学人教A版-三角函数-章节测试-10-含解析
1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年河北省唐山市高一上学期数学人教A版-三角函数-章节测试(10) 姓名:____________ 班级:____________ 学号:____________考试时间:120分钟 满分:150分题号一二三四五总分评分*注意事项:阅卷人得分一、选择题(共12题,共60分)1. 已知 , , 则的值为( ) A . B . C .D .2. 在平面直角坐标系中,角以射线为始边,终边与单位圆的交点位于第四象限,且横坐标为 , 则的值为( )A .B .C .D .π2π3. 函数 的最小正周期是( )A .B .C .D .第一象限第二象限第三象限第四象限4. 点在平面直角坐标系中位于( )A . B . C . D .5. 函数 的单调递减区间( )A .B .C .D .6. 函数 的定义域是( )A . B .C .D .[π+2kπ,3π+2kπ](k∈Z)7. 函数y=sin2x的单调减区间是( )A .B .C .D .8. 已知函数与 的图象对称轴完全相同,则函数 的对称中心可能为A .B .C .D .9. 若 且 则 的值是( )A .B .C .D .10. 已知函数 最小正周期为,且 的图象过点 ,则方程所有解的和为( )A . B . C . D .11. 将函数 的图像向左平移 个单位后,与函数 的图像重合,则函数 ( ).A .B .C .D .周期为 的奇函数周期为 的偶函数周期为 的奇函数周期为 的偶函数12. 函数 是( )A .B .C .D .13. 已知扇形的弧长为,半径为1,则扇形的圆心角为 ,扇形的面积为.14. 将函数 的图像向右平移 个单位长度后,所得函数为偶函数,则.15. 亲爱的考生,我们数学考试完整的时间是2小时,则从考试开始到结束,钟表的分针转过的弧度数为 .16. 函数 单调增区间为 .17. 已知 .(1) 化简;(2) 若为第四象限角且 , 求的值;(3) 若 , 求 .18. 已知函数 , , 将图象向右平移个单位,得到函数的图象.(1) 求函数的解析式,并求在上的单调递增区间;(2) 若函数 , 求的周期和最大值.19. 求函数 的定义域.20. 函数 的部分图像如图所示.(1) 求函数 的解析式;(2) 求图中 的值及函数 的单调递减区间;(3) 若将 的图象向左平移 个单位后,得到 的图像关于直线 对称,求 的最小值.21. 已知为斜三角形.(1) 证明:;(2) 若 , 求的值.答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.(1)(2)(3)18.(1)(2)19.20.(1)(2)(3)21.(1)(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
唐山市海港高级中学基础测试(四)(三角函数)
1
.终边在直线y =上的角的集合是()
A .{|2,}3k k πααπ=+∈Z B.2{|2,}3k k πααπ=+∈Z C .{|,}3k k πααπ=+∈Z D .2{|,}3k k πααπ=+∈Z
2.设集合{|18045,}2k M x x k ==+∈⋅ Z ,{|18045,}4
k
M x x k ==+∈⋅ Z , 那么( )
A .M N =
B .M N ⊆
C .N M ⊆
D .M N =∅ 3.若sin cos 0αα>,且
cos 0tan α
α
<,则角α是() A .第一象限角 B .第二象限角C .第三象限角 D .第四象限角 4.点(sin 2017,cos 2017)A
位于( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 5.若点55(sin
,cos )66
ππ
在角α的终边上,则sin α的值为( ) A
. B .12- C .1
2
D
6.若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的面积为( )
A .
21
sin 1
B .
22sin 2 C .21cos 1
D .22
cos 2
7.若,且为第四象限角,则的值等于()
A .
B .
C .
D . 8.若3sin cos 0αα+=,则
21
cos 2sin cos ααα
+的值为( )
A .103
B .53
C .2
3
D .-2
9.在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎫2x +π6,④y =tan ⎝
⎛⎭⎫2x -π
4中,最小正周期为π的
所有函数为( )
A .①②③
B .①③④
C .②④
D .①③ 10.已知>0,,直线=和=是函数图像的两条相邻的对
称轴,则=()
A .π4
B .π3
C .π2
D .3π
4
11.函数3sin(
2)5
y x π
=-的单调递增区间是(以下k ∈Z ) ( )
A .717[,]2020k k ππππ--
B .717[,]2020k k ππππ++
C .1317[,]2020k k ππ
ππ++D .719[,]2020
k k ππππ++
12.若将函数2sin(2)6
y x π
=+的图像向右平移1
4个周期后,所得图像对应的函数为()
A .2sin(2)4y x π
=+
B .2sin(2)3y x π=+
C .2sin(2)4y x π=-
D .2sin(2)3
y x π
=-
13.函数的部分图像如图所示,则y= 14.已知函数()tan()(0,||)2
f x A x π
ωϕωϕ=+><的最小正周期为
2
π
, 图象过两点(0,1)、3(
,0)8π,则()24
f π
=________. 15.如图,某港口一天6时到18时的谁深变化曲线近似满足函数
(
6
3)y sin x k π
=+Φ+,据此函数可知,这段时间水深(单位:m )
的最大值为___________.
16.设sin ,(0)()(1)1,(0)
x x f x f x x π<⎧=⎨-+≥⎩和1cos ,()
2()1(1)1,()2x x g x g x x π⎧
<⎪⎪=⎨
⎪-+≥⎪⎩
,则)4
3()65()31()41(f g f g +++的值为
5
sin 13
α=-αtan α125125-5125
12
-ω0ϕπ<<x 4
πx 54π
()sin()f x x ωϕ=+ϕ=sin()y A x ωϕ+
1.D 因为在(0,)π
内终边在直线y =上的角是23
π
,
所以终边在直线y =上的角的集合
为2{|,}3
k k π
ααπ=+∈Z .故选D . 2.B 由于M 中,180********(21)2
k x k k =+=+=+⋅⋅⋅
,21k +是奇数;而N 中,
180********(1)4
k x k k =+=+=+⋅⋅⋅ ,1k +是整数,因此必有M N ⊆.
3.C 由sin cos 0αα>可知sin α,cos α同号,从而α为第一或第三象限角.由
cos 0tan α
α
<可知cos α,tan α异号,从而α为第三或第四象限角.综上可知,α为第三象限角.故选C . 4.C 因为sin 2017sin(1118037)sin 370=⨯=-< +,cos2017cos(1118037)=⨯ + cos370=-< ,所以点(sin 2017,cos 2017)A 位于第三象限,故选C .
5.A
根据任意角的三角函数的定义,5cos 6sin 12
π
α==,故选A . 6.A
由题意得扇形的半径为1sin1
.又由扇形面积公式得,该扇形的面积为211
22sin 1⨯
⨯
21sin 1
=.故选A . 7.D 由,且为第四象限角,则,则
,故选D .
8.A 由3sin cos 0αα+=得cos 0α≠,所以1
tan 3
α=-,所以
2222
2211()1cos sin 1tan 1032cos 2sin cos cos 2sin cos 12tan 313
αααααααααα+-++===
=+++-. 9.A 函数y =cos|2x |=cos 2x ,其最小正周期为π,①正确;将函数y =cos x 的图像中位于x 轴上方的图像不变,位于x 轴下方的图像对称地翻转至x 轴上方,即可得到y =|cos x |的图像,所以其最
小天正周期也为π,②正确;函数y =cos ⎝⎛⎭⎫2x +π6的最小正周期为π,③正确;函数y =tan ⎝
⎛⎭⎫2x -π
4的最小正周期为π
2,④不正确.
0.A 由题设知,
=,所以=1,所以=(),
所以=(),因为,所以=
,故选A . 11.B 3sin(
2)3sin(2)55y x x ππ=-=--,只需求出3sin(2)5
y x π
=-的单调递减区间,由3222252k x k πππππ+≤-≤+得717222102k x k ππππ+≤≤+,所以7172020
k x k ππππ+≤≤+,
所以3sin(2)5y x π=-的单调递减区间为717[,]2020
k k ππ
ππ+
+.故选B . 12.D 函数2sin(2)6y x π=+的周期为π,将函数2sin(2)6y x π=+的图象向右平移1
4
个周期即
4
π个单位,所得函数为2sin[2()]2sin(2)463y x x πππ
=-+=-.故选D .
13.由图知,2A =,周期2[()]36T πππ=-=,所以23
πω=,所以
2s i n (2)
y x ϕ=+,因为图象过点(,2)3π,所以22sin(2)3πϕ=⨯+,所以2sin()13
πϕ+=,所以22()32k k ππϕπ+=+∈Z ,令0k =,得6πϕ=-,所以2sin(2)6
y x π=-. 14.2T ππω==,所以2ω=.因为图象过点3(
,0)8π,所以30tan(2)8
A π
ϕ=⨯+,即3()4k k πϕπ+=∈Z ,所以,因为||2πϕ<,所以4
π
ϕ=.再由图象过定点(0,1),得1A =.综上可知,()tan(2)4f x x π=+.所以()tan(2)24244f πππ=⨯
+tan 3π
==15.8由图像得,当时,求得,当时,
,故答案为8.
16.3因为22)4
1
(=
g ,5()16g =+,12()sin()1133f π=-+=, 3()sin()11442
f π=-+=-+,所以原式3=.
5sin 13α=-α12cos 13
α==sin tan cos ααα=5
12
=-πω544
ππ-ω4πϕ+2k π
π+k Z ∈ϕ4
k π
π+
k Z ∈0ϕπ<<ϕ4
π
2sin(2)6y x π
=-sin()16x π+Φ=-min 2y =5k =sin()16
x π
+Φ=max 3158y =⨯+=。
