稍复杂的分数除法问题
青岛版六年级数学上册6.4-稍复杂的分数除法问题同步练习及答案

6.4 稍复杂的分数除法问题
1.果园有枣树147棵,桃树比枣树多71,桃树有多少棵?
2.小英读一本故事书,第一天读了全书的 83 ,第二天读了余下的 52,
这时还剩下45页没有读。
这本书共有多少页?
3.某商站运进一批红糖,第一天卖出250千克,第二天卖出200千克,
两天正好卖出了这批红糖的 41,这批红糖有多少千克?
4. 学校图书馆购进科技书60本,比购进的故事书少 5
1。
学校图书
馆购进故事书多少本?
答案:1. 147×(1+71)= 168(棵)
2. 45÷[1-83-(1-83)× ]52
120(页) 3. (250+200)÷41 =1800(千克)
4. 60÷(1-5
1)= 75(本)
【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】。
小学数学稍复杂的分数除法应用题
多
2 3
,黑兔有多少只?
3、根据所给的方程口头编应用题。
ⅹ- 1 ⅹ= 60 5
ⅹ+ 1 ⅹ= 60 5
1、看图列算式。
(1) 男生 女生
(2) 桃树 李树
1
ⅹ人
多3
15人
ⅹ+
ⅹ 1
3
= 15
ⅹ棵
300棵
少
2 5
ⅹ
﹣
2 5
ⅹ
= 300
2、根据条件列方程解答。
• 小张买了一本书和一支钢笔,书的单价是
10
元
,
正好比钢笔的单价少
3 8
, 钢笔的单
价是多少元?
(2) 李明家有白兔450只, 白兔的只数比黑兔
复习
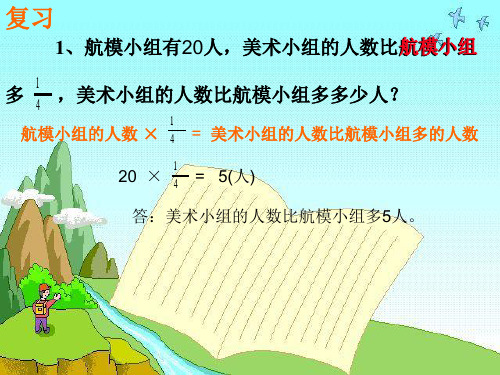
1、航模小组有20人,美术小组的人数比航模小组
多 1 ,美术小组的人数比航模小组多多少人?
1
航模小组的人数 × 4 = 美术小组的人数比航模小组多的人数
20
×
1 4
= 5(人)
答:美术小组的人数比航模小组多5人。
2、航模小组有20人,美术小组的人数比航模
小组多
1 4
。美术小组有多少人?
航模小组的人数 +美术小组比航模小组多的人数=美术小组的人数
Ⅹ
=
24×
4 3
Ⅹ = 16 答:航模小组有16人。
这类题的特点: 单位“1”是未知的。
解答这类题的关键:搞清楚哪两个量比较, 谁多谁少,多或少了谁的几分之几。
解答方法:
(1)找准单位“1”的量,设未知数为X。
(2)根据含有分率的句子找出等量关系。
(3)根据“一个数乘分数的意义”用乘法 列方程解答。
青岛版六年级数学上册第六单元分数四则混合运算信息窗稍复杂的分数除法问题课件

32
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
33
答: 这种马铃薯每百克含脂肪900毫克.
先乘
先减
30
青岛版六年级数学上册
• 第六单元分数四则混合运算信息窗4稍复杂 的分数除法问题
31
三、自主练习
5.星光小学举办“变废为宝, 美化校园”作品大赛, 六年级上 交作品160件, 比五年级多 1。
7
(1)本次活动五年级上交 (2)本次活动中,五、六年级学生
万寿山占 1 4
颐和园面积 - 万寿山面积 = 昆明湖面积
解:设颐和园的占地面积是 x 公顷
-=
3 4
x
= 219
x= 292
返回
答:颐和园的占地面积是292 公顷。6
青岛版六年级数学上册
• 第六单元分数四则混合运算信息窗4稍复杂 的分数除法问题
7
二、合作探索
颐和园的占地面积是多少公顷?
x 公顷 219
1.画线段图, 分析数量关系。
2.列等量关系式。
3.列式解答, 进行检验。
10
青岛版六年级数学上册
• 第六单元分数四则混合运算信息窗4稍复杂 的分数除法问题
11
二、合作探索
布达拉宫南北长多少米?
南北长: 东西长:
x米
360米
比南北长 1
5
12
青岛版六年级数学上册
• 第六单元分数四则混合运算信息窗4稍复杂 的分数除法问题
+ = 360
6
x
=
360
5
返回
x = 300
答: 布达拉宫南北长300米。
16
青岛版六年级数学上册
2024年青岛版(五年制)五年级数学上册教案第八单元 分数四则混合运算较复杂分数除法问题

较复杂分数除法问题⏹教学内容教材第110~113页,较复杂的分数除法⏹教学提示谁做单位“1”,是否求单位“1”。
⏹教学目标知识与能力能结合具体情境,运用分数四则混合运算解决稍复杂的分数除法问题。
会借助线段图,分析稍复杂的用分数四则混合运算解决的分数除法问题的数量关系,并解决问题。
过程与方法1.在解决问题的过程中,逐步掌握用分数四则混合运算解决稍复杂的分数除法问题的策略,提高分析问题和解决问题的能力。
2.经历把现实问题转化成数学问题的过程,进一步学习解决数学问题的思想和方法,养成科学探索问题的习惯。
情感、态度与价值观在探索未知的过程中体验学习的乐趣,培养学生积极、主动地参与学习和探究活动的态度。
⏹重点、难点重点:1.找单位“1”。
2.画线段图。
难点:分析题目中的数量关系。
教学准备教师准备:实物投影仪。
学生准备:练习本、直尺、铅笔。
教学过程(一)新课导入:师:通过前几课的资料链接,同学们应该知道,我国的世界文化遗产也很多,你能数一数吗?。
生……(师重点板书颐和园,布达拉宫和敦煌莫高窟。
)师:今天,老师带领大家继续了解颐和园,布达拉宫和敦煌莫高窟。
出示情境图信息。
生:感叹建筑的宏伟……师:同学们除了发现建筑的宏伟外,还发现了什么?生1:昆明湖占地219公顷,万寿山占地面积仅是颐和园的14。
生2:布达拉宫的东西长360米,比南北长15。
生3:敦煌莫高窟宽30米,宽比高少14。
生4:……师:根据图中的信息,结合前面所学知识,你能提出什么问题?生1:万寿山的占地面积是多少?生2:颐和园的占地面积是多少?生3:布达拉宫的南北长是都是米?生4:莫高窟的高是多少米?生5:布达拉宫的占地面积大约是多少米?生6:……设计意图:借助中国的世界文化遗产入手,引入情境图片,激发学生学习的热情。
引导学生发现数学信息,从而提出数学问题。
(二)探究新知:师:同学们竟然一口气提出了这么多的问题,看了前面的学习内容掌握的非常扎实。
由于课堂时间有限,这节课我们先来研究3个问题。
青岛版数学五年级上册 稍复杂的分数除法问题(2)

1
x ×(1- 4 )= 30
x × 3 = 30
4
x = 40
答:敦煌莫高窟最大石窟的高为40米。
想一想:两题有什么相同点和不同点?
课堂练习
1.“锅庄”是流行于青藏地区的大众性舞蹈。表演
一队有男演员12人,比女演
员少 。女演员有多少人?
解:设女演员有x人。
x ×(1- )= 12
南北长:
360米
1
x
5
东西长:
南北长
+
1
比南北长
5
东西比南北多的米数 = 东西长
解:设南北长是x米。
=
+
6
5
返回
宏大,它东西长360
1
米,比南北长
。
5
360
x = 360
x =
300
答:布达拉宫南北长300米。
西藏的布达拉宫规模
布达拉宫南北长多少米? xx 米
宏大,它东西长360
1
米,比南北长
。
5
1
年级上交作品160件,比五年级多 7 。
(1)本次活动五年级上交
作品多少件?
解:设五年级上交作品 x件。
x + 1 x = 160
7
8
7
x = 160
x = 140
答:五年级上交作品140件。
(2)本次活动中,五、六年级
学生作品总数占全校学生作品总
2
数的 5 。全校学生作品一共有多
少件?
解:设全校学生作品一共有 x 件。
8 中国的世界遗产——分数四则混合运算
稍复杂的分数除法问题(2)
稍复杂的分数除法问题

稍复杂的分数除法问题学习目标:1、我能在理解分数除法的意义及掌握分数乘法问题解题思路的基础上,掌握已知“一个数的几分之几是多少,求一个数”的稍复杂的分数除法问题的解题思路和方法,能比较熟练地解答一些简单的实际问题。
2、我能弄清单位“1”的量,会分析题中的数量关系(重、难点)。
3、我能借助线段图,分析稍复杂的分数除法应用题的数量关系。
学习过程:一、自主学习1、知识链接。
第二小组有9人,是第一小组人数的910,第一小组有几人?思考下面的问题:(1)信息:_______________________________ 问题:______________________________单位“1”:__________________________(2)线段图:(3)解题过程(两种方法):2、我会预习。
自学课本第84—85页,思考下面的问题。
(1)“万寿山占地面积仅是颐和园的14”是什么意思?是把谁看做单位“1”?这道题有什么样的数量关系?(2)“比南北长15”是什么意思?是把谁看做单位“1”?这道题有什么样的数量关系?(3)“宽比高少14”是什么意思?是把谁看做单位“1”?这道题有什么样的数量关系?(4)思考:通过预习,你还有哪些不明白的问题?___________________________二、合作探究1、红点问题一:颐和园的占地面积是多少公顷?思考:你能画出线段图,分析数量关系吗?你有几种解法?2、红点问题二:布达拉宫南北长多少米?思考:你能画出线段图,分析数量关系吗?应该先画什么?你有几种解法?3、红点问题三:敦煌莫高窟最大石窟的高为多少米?思考:你能画出线段图,分析数量关系吗?应该先画什么?你有几种解法?三、班级展示1、各小组将你们的研究成果向全班同学汇报。
2、汇报时,要回答其他小组提出的疑问。
四、梳理拓展说一说本节课你有什么收获。
(温馨提示:可以从知识性的收获、学习方法的收获、学习习惯、个人反思等几方面谈。
稍复杂的分数除法问题,六年级上册,第22课时

第22课时稍复杂的分数除法问题学习内容课本第38页例5,第40页练习八第6~10题。
学习目标进一步理解分数的意义,会用方程的方法解决稍复杂的分数除法问题。
课文讲解例5,比多少的分数问题。
两种量进行比较,用小明的体重去度量爸爸的体重,少的部分用分数表示。
画线段图分析数量关系。
未知数参与列式,有两种方法。
两步计算。
稍复杂的分数乘法问题,列方程解决分数除法的简单问题是本课的学习基础。
列方程解决稍复杂的分数除法问题,是本课的新知。
辅导精要例4,略读课文,了解课文的基本结构:用方程解决问题。
读题。
理解并记住长句“他的体重比爸爸的体重轻”、“轻8/15”下划线,少的部分用分数表示,爸爸的体重是一个未知数。
读步骤。
解决问题有三步骤:“阅读与理解——分析与解答——回顾与反思”。
第一步,阅读与理解。
摘抄条件和问题:小明的体重是35㎏,小明的体重比爸爸轻8/15,要求的是爸爸的体重。
第二步,分析与解答。
分析数量的对应关系:爸爸的体重与少的部分对应关系是“1→8/15”、“?㎏→?㎏”;爸爸的体重与小明体重的对应关系是“1→7/15”、“?㎏→35㎏”。
画图。
爸爸的体重与小明的体重是两个不同的量,画线段图需要有两条线段;由于“轻8/15”与“小明的体重”不相对应,它们不在同一线段上。
如图。
关系式。
爸爸的体重×(1-8/15)=小明的体重,或者爸爸的体重-轻的部分=小明的体重,列方程。
爸爸的体重是未知数。
解:设小明爸爸的体重是x㎏。
解法一:(1-8/15)x=35,7/15x=35,x=35×15/7,x=75。
解法二:x-8/15x=35,7/15x=35,x=35×15/7,x=75。
第三步,回顾与反思。
从答案入手进行检验,75㎏>35㎏,爸爸比小明重,答案是合理的。
进一步计算:(75-35)/75=8/15,或者35/75=7/15,1-7/15=8/15,符合题意,解答正确。
答:小明爸爸的体重是75㎏。
“稍复杂的分数(百分数)除法应用题”错误成因分析

“稍复杂的分数(百分数)除法应用题”错误成因分析1. 引言1.1 介绍在初中数学学习中,分数和百分数是学生经常接触到的知识点。
其中,分数除法是一个稍微复杂一些的应用题类型,需要学生灵活运用所学的分数和百分数知识进行计算。
然而,有些学生在解答这类题目时常常出现错误,造成分数除法的计算结果不正确。
接下来将通过分析分数除法应用题错误成因来探讨这些常见错误的背后原因,以期能帮助教师和学生更好地理解和掌握这一知识点。
在日常的教学实践中,教师常常会遇到学生在解答稍复杂的分数除法应用题时出现各种错误。
这些错误主要可以归结为学生未理解分数和百分数的含义、混淆分数和百分数的计算方法、忽视约分的重要性、计算过程中出现疏忽或错误以及缺乏实际应用题训练等方面。
通过分析这些错误的成因,我们可以更好地指导学生避免类似错误,提高他们对分数除法的理解和运用能力。
1.2 研究背景分数和百分数是数学中常见的概念和运算方式,是学生在数学学习中需要掌握和运用的重要知识点。
在学生学习过程中,我们经常会发现一些学生在进行稍复杂的分数(百分数)除法应用题时会出现各种错误。
这些错误不仅影响了他们的学习成绩,也反映了他们对分数和百分数的理解和应用能力存在着一定的困难和不足。
通过对学生在分数(百分数)除法应用题中常见的错误进行分析和总结,我们可以发现一些共同的成因。
这些成因包括未理解分数和百分数的含义,混淆分数和百分数的计算方法,忽视约分的重要性,计算过程中出现疏忽或错误,以及缺乏实际应用题训练等。
了解这些错误产生的原因,可以为我们在教学实践中提供一定的参考和指导,帮助学生更好地掌握和运用分数和百分数的知识,提高他们的数学学习成绩和能力。
2. 正文2.1 未理解分数和百分数的含义未理解分数和百分数的含义是导致稍复杂的分数(百分数)除法应用题错误的一个重要原因。
学生们在进行分数除法应用题时,如果没有正确理解分数和百分数的含义,就很容易在计算过程中出现错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
稍复杂的分数除法问题
数学一直以来都是一个令人头疼的学科,尤其是一些稍微复杂的问题。
在这篇文章中,我想和大家分享一些涉及到分数除法的稍微复杂一点的问题,以及如何解决它们。
问题1:如何将一个分数除以一个小数?
假设我们需要计算2/3除以0.2. 首先,我们需要将小数转化为分数形式。
因为0.2可以写成2/10或者1/5,我们在此选择将其转化为1/5。
所以,我们现在需要计算2/3 ÷ 1/5。
对于两个分数的除法,我们可以在不改变分数值的前提下,将除法运算转换成乘法运算:
2/3 ÷ 1/5 = 2/3 x 5/1
现在,我们可以将两个分数相乘:
2/3 x 5/1 = 10/3
所以,2/3 ÷ 0.2 = 10/3。
问题2:如何将一个分数除以另一个分数?
让我们考虑一下这个问题:5/7 ÷ 2/3。
一种解决方法是使用“翻
转和乘法”法则,将除法运算转换成乘法运算:
5/7 ÷ 2/3 = 5/7 x 3/2
现在我们可以将两个分数相乘:
5/7 x 3/2 = 15/14
所以,5/7 ÷ 2/3 = 15/14。
问题3:如何将一个分数除以一个分数,并将答案写成混合数?
让我们考虑这个问题:17/5 ÷ 2/3。
我们可以使用与前一个问题
相同的方法,将除法运算转换成乘法运算:
17/5 ÷ 2/3 = 17/5 x 3/2
现在我们可以将两个分数相乘:
17/5 x 3/2 = 51/10
此外,我们还可以将分数51/10转化为混合数的形式,这可以使答案更加易于理解:
51/10 = 5 + 1/10
所以,17/5 ÷ 2/3 = 5 1/10。
结论
通过解决这些稍微复杂的分数除法问题,我们可以看到,处理分数的关键在于能够将问题转化为相应的乘法运算,并进行必要的分数简化和转化。
当我们能够灵活地使用这些技巧时,我们可以更加自信地处理各种各样的数学问题。
