第8章立体几何专题4 垂直的证明常考题型专题练习——【含答案】
立体几何线面垂直-题型全归纳(解析版)

立体几何线面垂直-题型全归纳题型一利用等腰三角形“三线合一”例题1、如图,在正三棱锥P-ABC中,E,F,G分别为线段PA,PB,BC的中点,证明:BC⊥平面PAG。
证明:在正三棱锥P-ABC中,AB=AC,G是BC的中点,∴AG⊥BC,又 PB=PC,G是BC的中点,∴PG⊥BC,PG⋂AG=G,PG,AG⊂平面PAG,∴BC⊥平面PAG,解题步骤(1)根据线段的中点,找出相应的等腰三角形;(2)格式“因为D是BC的中点,且AB=AC,所以AD⊥BC”;(3)依据“三线合一”得到线线垂直。
变式训练1、已知四面体ABCD中,AB=AC,BD=CD,E为棱BC的中点,求证:AD⊥BC证明:连接DE,AB=AC,E是BC的中点,∴AE⊥BC,又 BD=CD,E是BC的中点,∴DE⊥BC,AE⋂DE=E,AE,DE⊂平面ADE,∴BC⊥平面ADE,AD⊂平面ADE,∴AD⊥BC变式训练2、在三棱锥P ABC -中,2AC BC ==,90ACB ∠=,AP BP AB ==,PC AC ⊥.求证:PC AB ⊥证明:取AB的中点O,连接OP,OC, AP=BP,O是AB的中点,∴PE⊥AB,又 AC=BC,O是AB的中点,∴OC⊥AB,PO⋂CO=O,PO,CO⊂平面POC,∴AB⊥平面POC,PC⊂平面POC,∴AB⊥PC。
变式训练3、如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,E为CD的中点,060=∠ABC ,求证:AB⊥平面PAE。
证明: 底面ABCD是菱形,060=∠ABC ,∴AE⊥CD,又 AB//CD,∴AB⊥AE,又PA⊥平面ABCD,AB⊂平面ABCD,∴AB⊥PA,AP⋂AE=A,AP,AE⊂平面PAE,∴AB⊥平面PAE。
A CB P题型二利用勾股定理逆定理例题2、如图,在正方体1111D C B A ABCD -中,M 为棱1CC 的中点,AC 交BD 于点O ,求证:BDM1平面⊥O A 证明:连接OM,M A 1,11C A ,设正方体的棱长为2,则6222222121=+=+=AO A A O A 32122222=+=+=OC CM OM 91)22(222121121=+=+=M C C A M A 21221M A OM O A =+∴即:OM⊥OA 1又 在正方体1111D CB A ABCD -中,∴BD⊥OA 1 OM,BD⊂平面BDM,∴BDM1平面⊥O A 解题步骤(1)根据题干给出的线段长度(没有长度的可以假设),标示在图形上,找出相应的三角形;(2)把线段的长度分别求平方,判断能否构成“222c b a =+”;(3)根据平方关系得到线线垂直。
专题4:立体几何中垂直关系的证明基础练习题

12.证明见解析
【分析】
在等腰三角形PAB中, 是 的中点,可得 ,利用线面垂直的判定定理可证 平面 ,利用线面垂直的性质定理,即可得证.
【详解】
证明:∵ 是 的中点, ,
∴ ,
∵ 底面 ,
∴ ,
又∵ ,即
∴ 平面 ,
∴ ,
∵ 平面 , 平面 ,
∴ 平面 ,
∵ 平面 ,
∴ .
8.证明见解析
【分析】
由平面 ⊥平面 得到 ⊥平面 ,进一步得到 ⊥ ,再结合直径所对圆周角为直角得到 ⊥ , ⊥平面 ,从而得到证明.
【详解】
由题设知,平面 ⊥平面 ,交线为 .
因为 ⊥ , 平面 ,所以 ⊥平面 ,故 ⊥ .
因为 为 上异于 , 的点,且 为直径,所以 ⊥ .
又 = ,所以 ⊥平面 .
∴点O为三角形ABC的垂心,∴BO⊥AC
又因PO⊥AC,所以AC⊥PBO
故PB⊥AC
考点:证明异面直线垂直.
7.见解析
【分析】
由已知中P为正方形ABCD所在平面外一点,PA⊥面ABCD,结合正方形的几何特征,我们易得到BC⊥平面PAB,由线面垂直的性质得到BC⊥AE,结合已知中AE⊥PB,及线面垂直的判定定理,得到AE⊥平面PBC,最后再由线面垂直的判定定理,即可得到AE⊥PC.
【点睛】
此题考查线面垂直的性质和判定的综合应用,利用线面垂直得线线垂直.
5.证明见解析
【分析】
先证直线 平面 ,再证平面 ⊥平面 .
【详解】
证明:∵ 是圆的直径, 是圆上任一点, , ,
平面 , 平面 ,
,又 ,
平面 ,又 平面 ,
平面 ⊥平面 .
【点睛】
人教A版必修二立体几何面面垂直证明线面垂直习题-含答案

垂直证明习题——面面垂直⇒线面垂直1. 如图,四边形ABCD 为矩形,平面ABEF ⊥平面ABCD , 90BAF ∠=︒.求证:AF ⊥平面ABCD .2. 在斜三棱柱111ABC A B C -中,侧面11AA CC ⊥平面ABC ,1AC CA =,AB AC ⊥,D 是1AA 的中点.求证:CD ⊥平面1AB .3. 如图,正方形ABCD 边长为a ,平面ABCD ⊥平面CED ,CE ⊥DE ,CE =12AB .证明:AE ⊥EC .4. 如图,在直角梯形ABCD 中,//AB DC ,90BAD ∠=,4AB =,2AD =,3DC =,点E 在CD 上,且2DE =,将ADE 沿AE 折起,使得平面ADE ⊥平面ABCE (如图).G 为AE 中点.求证:DG ⊥平面ABCE5. 如图在四棱锥P ABCD -中,底面ABCD 是矩形,点E 、F 分别是棱PC 和PD 的中点.若AP AD =,且平面PAD ⊥平面ABCD ,证明:AF ⊥平面PCD .6. 如图,四棱锥,,,,为等边三角形,平面平面,为中点.求证:平面.7. 如图,在四棱锥中,底面是矩形,侧面底面,且,若、分别为、的中点.求证:平面.8. 如图,四棱锥P —ABCD 的底面ABCD 是平行四边形,平面PBD ⊥平面ABCD ,PB =PD ,PA ⊥PC ,CD ⊥PC ,O ,M 分别是BD ,PC 的中点,连结OM .求证:OM ⊥平面PCD .P ABCD -//AB CD 90BCD ∠=︒224AB BC CD ===PAB ∆PAB ⊥ABCD Q PB AQ ⊥PBC P ABCD -ABCD PAD ⊥ABCD 2PA PD AD ==E F PC BD EF ⊥PDC9. 如图,在四棱锥中P ABCD -中,底面ABCD 是菱形,且60DAB ∠=︒,PA PD =,M 为CD的中点,平面PAD ⊥平面ABCD .求证:BD PM ⊥.10. 已知四棱锥中,底面是菱形,侧面平面,且,.证明:平面.11. 如图,在四棱锥P ABCD-中,侧面PCD⊥底面ABCD ,PD CD ⊥,底面ABCD 是直角梯形,,90,1,2AB CD ADC AB AD PD CD ∠=︒====.求证:BC ⊥平面PBD .12. 如图,在梯形ABCD 中,//,1,60AB CD AD DC CB ABC ︒===∠=,四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,1CF =.求证:BC ⊥平面ACFE .A P ABCD -ABCD PAD ⊥ABCD PA =1AD =2PD =DB ⊥PAC垂直证明习题——面面垂直⇒线面垂直(教师版)1. 如图,四边形ABCD 为矩形,平面ABEF ⊥平面ABCD , 90BAF ∠=︒.求证:AF ⊥平面ABCD .【解析】证明:∵90BAF ∠=︒,∴AB AF ⊥,又平面ABEF ⊥平面ABCD ,平面ABEF平面ABCD AB =,AF ⊂平面ABEF ,∴AF ⊥平面ABCD .2. 在斜三棱柱111ABC A B C -中,侧面11AA CC ⊥平面ABC ,1AC CA =,AB AC ⊥,D 是1AA 的中点.求证:CD ⊥平面1AB .【解析】证明:∵面11ACC A ⊥面ABC ,AB AC ⊥,∴AB ⊥面11ACC A ,即有AB CD ⊥. 又1AC A C =,D 为1AA 中点,则1CD AA ⊥.∴CD ⊥面11ABB A .3. 如图,正方形ABCD 边长为a ,平面ABCD ⊥平面CED ,CE ⊥DE ,CE =12AB .证明:AE ⊥EC .【解析】证明:∵平面ABCD ⊥平面CDE ,平面ABCD ∩平面CDE =CD ,AD ⊥CD , ∴AD ⊥平面CDE ,又EC ⊂平面CDE ,∴AD ⊥EC又∵CE ⊥DE ,AD ∩DE =D ,AD ,DE ⊂平面ADE ,∴CE ⊥平面ADE , 又AE ⊂平面ADE ,∴CE ⊥AE .4. 如图,在直角梯形ABCD 中,//AB DC ,90BAD ∠=,4AB =,2AD =,3DC =,点E在CD 上,且2DE =,将ADE 沿AE 折起,使得平面ADE ⊥平面ABCE (如图).G 为AE 中点.求证:DG ⊥平面ABCE【解析】证明:因为G 为AE 中点,2AD DE ==,所以DG AE ⊥.因为平面ADE ⊥平面ABCE ,平面ADE 平面ABCE AE =,DG ⊂平面ADE , 所以DG ⊥平面ABCE .5. 如图在四棱锥P ABCD -中,底面ABCD 是矩形,点E 、F 分别是棱PC 和PD 的中点.若AP AD =,且平面PAD ⊥平面ABCD ,证明:AF ⊥平面PCD .【解析】证明:在矩形ABCD 中,AD CD ⊥,又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,CD ⊂面ABCD , 所以CD ⊥平面PAD ,又AF ⊂面PAD ,所以CD AF ⊥①因为PA AD =且F 是PD 的中点,所以AF PD ⊥,②由①②及PD ⊂面PCD ,CD ⊂面PCD ,PD CD D =,所以AF ⊥平面 PCD . 6. 如图,四棱锥,,,,为等边三角形,平面平面,为中点.求证:平面.P ABCD -//AB CD 90BCD ∠=︒224AB BC CD ===PAB ∆PAB ⊥ABCD Q PB AQ ⊥PBC【解析】证明:因为,,所以,又平面平面,且平面平面,所以平面. 又平面,所以,因为为中点,且为等边三角形,所以.又,所以平面.7. 如图,在四棱锥中,底面是矩形,侧面底面,且,若、分别为、的中点.求证:平面.【解析】因为平面平面,平面平面,平面,又由矩形得,所以CD ⊥平面.又平面,∴,因为,∴又,所以是等腰直角三角形,且,即 又,∴而,平面,平面,所以平面 8. 如图,四棱锥P —ABCD 的底面ABCD 是平行四边形,平面PBD ⊥平面ABCD ,PB =PD ,PA ⊥PC ,CD ⊥PC ,O ,M 分别是BD ,PC 的中点,连结OM .求证:OM ⊥平面PCD .【解析】连结PO ,因为且O 是BD 中点,所以又因为平面平面,平面平面,平面,//AB CD 90BCD ∠=︒AB BC ⊥PAB ⊥ABCD PAB ⋂ABCD AB =BC ⊥PAB AQ ⊂PAB BC AQ ⊥Q PB PAB ∆PB AQ ⊥PB BC B ⋂=AQ ⊥PBC P ABCD -ABCD PAD ⊥ABCD 2PA PD AD ==E F PC BD EF ⊥PDC PAD ⊥ABCD PAD ⋂ABCD AD =CD ⊂ABCD ABCD CD AD ⊥PAD PA ⊂PAD CD PA ⊥//EF PA CD EF⊥2PA PD AD ==PAD ∆π2APD ∠=PA PD ⊥//EF PA PD EF ⊥CD PD D ⋂=CD ⊂PDC PD ⊂PDC EF ⊥PDC PB PD =PO BD ⊥PBD ⋂ABCD BD =PBD ⊥ABCD PO ⊂PBD。
高中数学第八章立体几何初步-平面与平面垂直的判定课件及答案

则 AD⊥BC,SD⊥BC,∴∠ADS 为二面角 A-BC-S 的平面角.在 Rt△BSC
中,∵SB=SC=a,
∴SD=
22a,BD=B2C=
2 2 a.
在 Rt△ABD 中,AD= 22a.在△ADS 中, ∵SD2+AD2=SA2,∴∠ADS=90°,即二面角 A-BC-S 为直二面角,故平
面 ABC⊥平面 SBC.
(3)垂线法.过二面角的一个面内异于棱上的 A 点向另一个平面作垂线,垂 足为 B,由点 B 向二面角的棱作垂线,垂足为 O,连接 AO,则∠AOB 为二面 角的平面角或其补角.如图③,∠AOB 为二面角 α-l-β 的平面角.
【对点练清】
1.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两
D.AO⊥l,BO⊥l,且 AO⊂α,BO⊂β 答案:D
3.如图,在正方体 ABCD-A1B1C1D1 中,二面角 A-BC-A1 的平面 角等于 ________. 答案:45°
知识点二 平面与平面垂直
(一)教材梳理填空 1.面面垂直的定义:
一般地,两个平面相交,如果它们所成的二面角是_直__二__面__角__,就说 定义
D.不存在
()
答案:C 3.若平面 α⊥平面 β,平面 β⊥平面 γ,则
()
A.α∥γ
B.α⊥γ
C.α 与 γ 相交但不垂直 答案:D
D.以上都有可能
题型一 二面角的概念及其大小的计算
【学透用活】 (1)一个二面角的平面角有无数个,它们的大小是相等的. (2)构成二面角的平面角的三要素:“棱上”“面内”“垂直”,即二面角的 平面角的顶点必须在棱上,角的两边必须分别在两个半平面内,角的两边必须都 与棱垂直,这三个条件缺一不可. (3)当二面角的两个半平面重合时,规定二面角的大小是 0°;当二面角的两 个半平面合成一个平面时,规定二面角的大小是 180°,所以二面角的平面角 α 的取值范围是 0°≤α≤180°.
线面垂直练习题及答案

线面垂直练习题及答案线面垂直是立体几何中的一个重要概念,它指的是一条直线与一个平面垂直。
在解决线面垂直问题时,我们通常需要利用相关的定理和性质来进行证明和计算。
以下是一些线面垂直的练习题及答案。
练习题1:已知直线AB与平面α垂直,点C在平面α内,求证:直线AC垂直于平面α。
答案1:由于直线AB垂直于平面α,根据线面垂直的性质定理,直线AB与平面α内的所有直线都垂直。
因此,直线AC作为平面α内的一条直线,必然与直线AB垂直。
根据线面垂直的定义,直线AC也垂直于平面α。
练习题2:在长方体ABCD-EFGH中,求证:直线BF垂直于平面ABEF。
答案2:由于长方体的对角线BF是连接两个相对顶点的直线,根据长方体的性质,对角线BF垂直于底面ABCD和顶面EFGH。
因此,直线BF垂直于平面ABEF内的任意直线,满足线面垂直的定义。
练习题3:已知直线l与平面α相交于点P,且直线m垂直于平面α,求证:直线m与直线l垂直。
答案3:由于直线m垂直于平面α,根据线面垂直的性质,直线m与平面α内的所有直线都垂直。
由于直线l与平面α相交于点P,我们可以将直线l投影到平面α上,得到一个与l平行的直线。
由于直线m垂直于平面α,它也垂直于平面α内的任何直线,包括l的投影。
因此,直线m与直线l垂直。
练习题4:在三棱锥P-ABC中,若PA⊥平面ABC,且AB⊥AC,求证:平面PAB垂直于平面PAC。
答案4:由于PA垂直于平面ABC,根据线面垂直的性质,PA也垂直于平面ABC 内的所有直线,包括AB和AC。
由于AB垂直于AC,根据面面垂直的判定定理,如果一个平面内的两条相交直线都垂直于另一个平面,则这两个平面垂直。
因此,平面PAB垂直于平面PAC。
练习题5:已知直线a与平面α垂直,直线b在平面α内,且直线a与直线b 相交于点O,求证:点O是直线a上的垂足。
答案5:由于直线a垂直于平面α,根据线面垂直的性质,直线a与平面α内的所有直线都垂直。
初中数学证明垂直问题专题训练含答案

初中数学证明垂直问题专题训练含答案姓名:__________ 班级:__________考号:__________一、综合题(共3题)1、如图,四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.2、如图,四边形是平行四边形,,,是的中点,是延长线上一点.(1)若,求证:;(2)在(1)的条件下,若的延长线与交于点,试判定四边形是否为平行四边形?并证明你的结论(请先补全图形,再解答);(3)若,与垂直吗?若垂直给出证明,若不垂直说明理由.3、如图16,已知△ABC为等边三角形,P为BC上一点,△APQ为等边三角形。
(1)求证:AB∥CQ;(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并给予证明;若AQ 与CQ不能互相垂直,请说明理由。
二、计算题(共1题)1、如图,在中,,是边上的高,是边上的一个动点(不与重合),,,垂足分别为.(1)求证:;(2)与是否垂直?若垂直,请给出证明;若不垂直,请说明理由;(3)当时,为等腰直角三角形吗?并说明理由.三、解答题(共4题)1、完成下面证明:(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b证明:∵a⊥c(已知)∴∠1=(垂直定义)∵b∥c (已知)∴∠1=∠2()∴∠2=∠1=90° ()∴a⊥b()(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE证明:∵AB∥CD (已知)∴∠B=()∵∠B+∠D=180° (已知)∴∠C+∠D=180° ()∴CB∥DE()2、如图所示,已知AE与CE分别是∠BAC,∠ACD的平分线,且∠1+∠2=∠AEC.(1)请问:直线AE与CE互相垂直吗?若互相垂直,给予证明;若不互相垂直,说明理由;(2)试确定直线AB,CD的位置关系并说明理由.3、直线,与的平分线交于点C,过点C作一条直线分别与直线PA,QB相交于点D,E.(1)如图(1),当直线l与PA垂直时,求证:.(2)如图(2),当直线l与PA不垂直且点D,E在AB同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由.(3)当直线l与PA不垂直且点D,E在AB异侧时,(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,请写出AD,BE,AB之间的数量关系(不用证明).4、已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
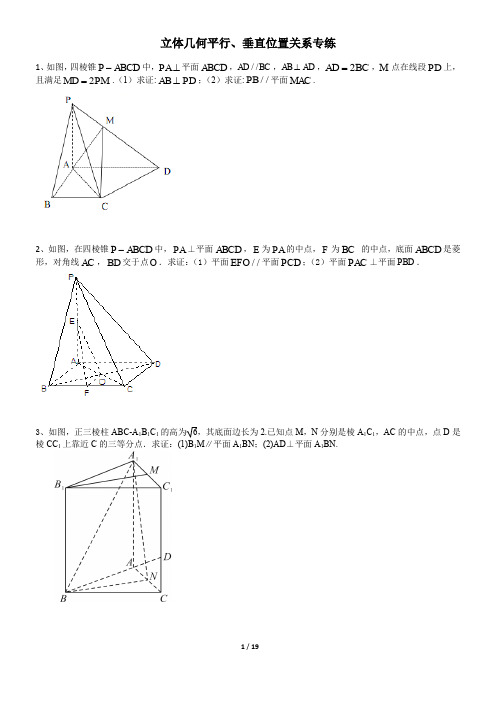
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1垂直的证明【方法总结】1、证明线面垂直的方法:①利用线面垂直定义:如果一条直线垂直于平面内任一条直线,则这条直线垂直于该平面;②用线面垂直判定定理:如果一条直线与平面内的两条相交直线都垂直,则这条直线与平面垂直;③用线面垂直性质:两条平行线中的一条垂直于一个平面,则另一条也必垂直于这个平面.2、证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.3、证明面面垂直一般要先找到两个面的交线,然后再在两个面内找能与交线垂直的直线,最后通过证明线面垂直证明面面垂直。
【分类练习】考向一 线面垂直例1、在四棱锥P ABCD -中,PA ⊥底面ABCD ,//AB CD ,AB BC ⊥,1AB BC ==,2DC =,点E 在PB 上求证:CA 平面PAD;【答案】(1)证明见解析;(2)2.【解析】(1)过A作AF⊥DC于F,则CF=DF=AF,所以∠DAC=90°,即AC⊥DA,又PA⊥底面ABCD,AC⊂面ABCD,所以AC⊥PA,因为PA、AD⊂面PAD,且PA∩AD=A,所以AC⊥平面PAD.例2、如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.11(1)证明:BE ⊥平面EB 1C 1;解析:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .例3、如图,在三棱柱111ABC A B C -中,1CC ⊥平面ABC ,D ,E ,F ,G 分别为1AA ,AC ,11A C ,1BB 的中点C 1B 1A 1GFE DCBA求证:AC ⊥平面BEF ;1【解析】(1)在三棱柱111ABC A BC -中,∵1CC ⊥平面ABC , ∴四边形11A ACC 为矩形.又E ,F 分别为AC ,11A C 的中点, ∴AC ⊥EF . ∵AB BC =. ∴AC ⊥BE , ∴AC ⊥平面BEF .例4、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,CD ⊥AD ,BC ∥AD ,12BC CD AD ==.(Ⅰ)求证:BD ⊥平面PAB ;【解析】因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以BD ⊥PA .在直角梯形ABCD 中,12BC CD AD ==,由题意可得2AB BDBC==,所以222AD AB BD=+,所以BD AB⊥.因为PA AB A=,所以BD⊥平面PAB.【巩固练习】1、如图,在三棱柱ABC-A1B1C1中,AB=AC,A1在底面ABC的射影为BC的中点,D 是B1C1的中点.证明:A1D⊥平面A1BC;【答案】见解析【解析】证明:设E为BC的中点,连接A1E,AE.由题意得A1E⊥平面ABC,所以A1E⊥AE.11因为AB =AC ,所以AE ⊥BC.故AE ⊥平面A 1BC.连接DE ,由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B,从而DE ∥A 1A 且DE =A 1A ,所以AA 1DE 为平行四边形.于是A 1D ∥AE. 因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC.2.(2019·上海格致中学高三月考)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD DC =,E 是PC 的中点,作EF PB ⊥交PB 于点F .(1)证明:PA ∥平面EDB ; (2)证明:PB ⊥平面EFD .【答案】(1)详见解析;(2)详见解析.【解析】(1)设AC 与BD 相交于O ,连接OE ,由于O 是AC 中点,E 是PC 中点,所以OE 是三角形PAC 的中位线,所以//PA OE ,而PA ⊂平面EDB ,OE ⊂平面EDB ,1所以PA ∥平面EDB.(2)由于PD ⊥底面ABCD ,所以PD BC ⊥,由于,BC CD PD CD D ⊥⋂=,所以BC ⊥平面PCD ,所以BC DE ⊥.由于DP DC =且E 是PC 中点,所以DE PC ⊥,而PC BC C ⋂=,所以DE ⊥平面PBC ,所以DE PB ⊥.依题意EF PB ⊥,DE EF E =,所以PB ⊥平面EFD .3.(2019·江苏高三月考)如图,在四棱锥P ABCD -中,四边形ABCD 是平行四边形,AC ,BD 相交于点O ,OP OC =,E 为PC 的中点,PA PD ⊥.(1)求证://PA 平面BDE ; (2)求证:PA ⊥平面PCD 【答案】(1)详见解析(2)详见解析 【解析】(1)连结OE .1因为四边形ABCD 是平行四边形,AC ,BD相交于点O ,所以O 为AC 的中点. 因为E 为PC 的中点,所以//OE PA .因为OE ⊂平面BDE ,PA ⊄平面BDE ,所以//PA 平面BDE .(2)因为OP OC =,E 为PC 的中点,所以OE PC ⊥. 由(1)知,//OE PA ,所以PA PC ⊥.因为PA PD ⊥,PC , PD ⊂平面PCD ,PC PD P ⋂=,所以PA ⊥平面PCD .考向二 面面垂直例1、如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,且2AB =,1BC =,E ,F 分别是AB ,PC 的中点,PA DE ⊥.旗开得胜1(1)求证://EF 平面PAD ; (2)求证:平面PAC ⊥平面PDE . 【答案】(1)详见解析(2)详见解析【解析】证明:(1)取PD 中点G ,连AG ,FG ,F ,G 分别是PC ,PD 的中点//FG CD ∴,且12FG CD = 又E 为AB 中点//AE CD ∴,且12AE CD =//AE FG ∴,AE FG =四边形AEFG 为平行四边形//EF AG ∴,又EF ⊄平面PAD ,AG ⊂平面PAD //EF ∴平面PAD(2)设AC DE H =由AEHCDH ∆∆及E 为AB 中点旗开得胜1得12AH AE CH CD == 又2AB =,1BC =3AC ∴=,1333AH AC ==23AH AB AE AC ∴==又BAD ∠为公共角GAE BAC ∴∆∆90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥,PAAC A =DE ⊥平面PAC ,又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;MD CBA【解析】(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD上异于C,D的点,且DC为直径,所以DM⊥CM.又BC CM=C,所以DM⊥平面BMC.而DM⊂平面AMD,故平面AMD⊥平面BMC.例3、如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=3π,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=AD,点M在线段EF上。
(1)求证:BC⊥平面ACFE;(2)若12EMMF=,求证:AM∥平面BDF.【答案】(1)证明见解析(2)证明见解析【解析】(1)在梯形ABCD中,∵AB∥CD,AD=CD=CB=a,∠ABC=60°∴四边形ABCD是等腰梯形且∠DCA=∠DAC=30°,∠DCB=120°∴∠ACB=∠DCB-∠DCA=90°∴AC⊥BC又∵平面ACFE⊥平面ABCD,交线为AC,∴BC⊥平面ACFE.(2)在梯形ABCD中,设AC BD=N,连接FN,则CN:NA=1:211又∵EM :MF =1:2,而EF=AC∴MF ∥AN ,且MF =AN ∴四边形ANFM 是平行四边形,∴AM ∥NF 又∵NF ⊂平面BDF ,AM ⊄平面BDF ∴AM ∥平面BDF .【巩固练习】1.如图,四面体P ABC -中,13PAPB ,平面PAB ⊥平面ABC ,90ACB ∠=︒,86AC BC ,,则PC_______.【答案】13【解析】取AB 的中点E ,连接,PE EC .1因为90,8ACBAC,6BC =,所以10AB =,所以5CE =.因为13PAPB ,E 是AB 的中点,所以,12PEAB PE .因为平面PAB ⊥平面ABC ,平面PAB ⋂平面ABC AB =,PE ⊂平面PAB , 所以PE ⊥平面ABC .因为CE ⊂平面ABC ,所以PE CE ⊥. 在Rt PEC ∆中,2213PCPE CE .2.如图,已知四边形ABCD 是矩形,PA ⊥平面ABCD ,M ,N 分别是AB ,PC 的中点.(1)求证:MN CD ⊥.(2)若PA AD =,求证:平面MND ⊥平面PDC . 【答案】(1)见解析;(2)见解析【解析】(1)证明:连接AC .过点N 作NO AC ⊥于点O ,连接OM .PA ⊥平面ABCD ,PA AC ∴⊥.又//PA NO ,NO ∴⊥平面ABCD ,且N 为PC 的中点,知O 为AC 中点,QM 为MN 在平面ABCD 内的射影,显然OMAB ⊥,MN AB ∴⊥.//AB CD ,MN CD ∴⊥1(2)连接,PM MC ,由PA AD BC ==,AM MB =,PA AM ⊥,MB BC ⊥,可知PM MC =.又N 为PC 的中点,MN PC ∴⊥.又MN DC ⊥,MN ∴⊥平面PCD ,∴平面MND ⊥平面PCD .3.(2019·北京高一期末)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,对角线AC ,BD 交于点O .(Ⅰ)若AC PD ⊥,求证:AC ⊥平面PBD ; (Ⅱ)若平面PAC ⊥平面ABCD ,求证:PB PD =;(Ⅲ)在棱PC 上是否存在点M (异于点C ),使得BM ∥平面PAD ?说明理由. 【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)不存在,理由详见解析. 【解析】(Ⅰ)证明:因为底面ABCD 是菱形, 所以AC BD ⊥.因为AC PD ⊥,BD PD D =,,BD PD ⊂平面PBD ,所以AC ⊥平面PBD . (Ⅱ)证明:连接PO .1由(Ⅰ)可知AC BD ⊥. 因为平面PAC ⊥平面ABCD , 所以BD ⊥平面PAC . 因为PO ⊂平面PAC , 所以BD PO ⊥. 因为底面ABCD 是菱形, 所以BO DO =. 所以PB PD =.(Ⅲ)解:不存在,证明如下.假设存在点M (异于点C ),使得BM 平面PAD . 因为菱形ABCD 中,BC AD ,且BC ⊄平面PAD , 所以BC 平面PAD .又因为BM ⊂平面PBC ,所以平面PBC 平面PAD . 这显然矛盾!旗开得胜1从而,棱PC 上不存在点M ,使得BM ∥平面PAD考向三 线线垂直例1、如图,ABC ∆和BCD ∆所在平面互相垂直,且2AB BC BD ===,0120ABC DBC ∠=∠=,E 、F 分别为AC 、DC 的中点.(Ⅰ)求证:EF BC ⊥ADCBFE【解析】(Ⅰ)∵,BC BD DF FC ==,且120CBD ∠=︒,∴ΔBCF 为RT 三角形,FC BF ⊥.同理,∵,BC BA AE EC ==,且120ABC ∠=︒,ΔBCE 为RT 三角形BE EC ⊥,∴ΔBCF ≅ΔBCE ,过E 作EO BC ⊥,垂足为O ,连接OF , 可证出EOC FOC ∆≅∆,旗开得胜1所以2EOCFOC π∠=∠=,即FO BC ⊥.从而证出BC ⊥面EOF ,又EF ⊂面EOF ,所以EF BC ⊥.BCDAFEO例2、如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,1BAA ∠=60°.(Ⅰ)证明1AB A C ⊥; 【解析】(Ⅰ)取AB 中点E ,连结CE ,1A B ,1A E ,∵AB =1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB , ∵CA =CB , ∴CE ⊥AB , ∵1CE A E ⋂=E ,∴AB ⊥面1CEA , ∴AB ⊥1A C ;1例3、如图,直三棱柱111C B A ABC -中,112ACBC AA ==,D 是棱1AA 的中点,BD DC ⊥1.(Ⅰ)证明:BC DC ⊥1;【解析】(Ⅰ)在Rt DAC ∆中,AD AC =,得:45ADC ︒∠=同理:1114590A DC CDC ︒︒∠=⇒∠=得:111,DC DC DC BD DC ⊥⊥⇒⊥面1BCD DC BC ⇒⊥【巩固练习】1、如图,在直棱柱111ABC A B C -中,BC AC ⊥,1AC CC =,D ,E 分别是棱AB ,AC 上的点,且//BC 平面1A DE .1(1)证明:DE 11B C ; (2)求证:11AC A B ⊥.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)因为//BC 平面1A DE ,BC ⊂平面ABC ,平面ABC 平面1A DE DE =,所以//BC DE .又在直棱柱111ABC A B C -中,有11//BC B C ,所以11//B C DE .(2)连接1A C ,因为棱柱111ABC A B C -为直棱柱,所以1CC ⊥平面ABC , 又BC ⊂平面ABC ,所以1BC CC ⊥.又因为BC AC ⊥,AC ⊂平面11ACC A ,1CC ⊂平面11ACC A ,1ACCC C =,所以BC ⊥平面11ACC A .又1AC ⊂平面11ACC A ,所以1BC AC ⊥. 在直棱柱111ABC A B C -中,有四边形11AAC C 为平行四边形. 又因为1AC CC =,所以四边形11AAC C 为菱形,所以11AC A C ⊥. 又1BCAC C =,BC ⊂平面1A BC ,1AC ⊂平面1A BC , 所以1AC ⊥平面1A BC ,又1A B ⊂平面1A BC ,所以11AC A B ⊥.2.(2019·四川双流中学高三月考(文))如图,在三棱锥A BCD -中,AB AD ⊥,BC BD ⊥,平面ABD ⊥平面BCD ,点E ,F (E 与A ,D 不重合)分别在棱AD ,BD 上,且EF AD ⊥.1(1)证明://EF 平面ABC . (2)证明:AD AC ⊥【答案】(1)详见解析(2)详见解析【解析】(1)在平面ABD 内,因为AB AD ⊥,EF AD ⊥,所以//EF AB . 又因为EF ⊄平面ABC ,AB平面ABC ,所以//EF 平面ABC .AD AC ⊥(2)因为平面ABD ⊥平面BCD ,平面ABD ⋂平面BCD BD =,BC ⊂平面BCD ,BC BD ⊥,所以BC ⊥平面ABD .因为AD ⊂平面ABD ,所以BC AD ⊥. 又AB AD ⊥,BCAB B =,AB 平面ABC ,BC ⊂平面ABC ,所以AD ⊥平面ABC ,又因为AC ⊂平面ABC ,所以AD AC ⊥.13、如图,在三棱锥A -BCD 中,点M ,N 分别在棱AC ,CD 上,且N 为CD 的中点。
