fisher算法及其matlab实现
fisheriris数据集matlab中knn分类 -回复

fisheriris数据集matlab中knn分类-回复如何使用Matlab中的KNN分类算法对Fisheriris数据集进行分类。
第一步是导入数据集。
在Matlab中,可以使用内置函数`load fisheriris`来加载Fisheriris数据集。
该数据集包含150个样本,每个样本有4个特征(萼片长度、萼片宽度、花瓣长度、花瓣宽度)。
此外,每个样本还有一个类标签,表示鸢尾花的类别。
matlabload fisheriris第二步是观察数据集。
可以使用Matlab的命令行窗口或数据编辑器来查看数据集的内容。
在命令行窗口中输入`fisheriris`可以显示数据集的前若干行。
第三步是划分训练集和测试集。
为了评估分类器的性能,我们需要将数据集划分为训练集和测试集。
可以使用Matlab内置函数`cvpartition`来实现随机划分。
matlabc = cvpartition(species,'HoldOut',0.3);trainIdx = training(c);testIdx = ~trainIdx;这里我们将数据集划分为70的训练集和30的测试集。
`trainIdx`和`testIdx`是逻辑向量,指示哪些样本属于训练集和测试集。
第四步是选择KNN算法的参数。
在Matlab中,可以使用`fitcknn`函数创建一个分类器对象,并设置相关参数。
常用的参数有:- 'NumNeighbors':指定邻居的数量。
- 'Distance':指定距离度量的类型,如'euclidean'、'cityblock'等。
matlabknn = fitcknn(meas(trainIdx,:), species(trainIdx),'NumNeighbors',5,'Distance','euclidean');在这个例子中,我们选择最近的5个邻居来进行分类,并使用欧氏距离作为距离度量。
matlab fisher最优分割 时间序列

在MATLAB中,可以使用以下步骤来实现Fisher最优分割算法对时间序列进行聚类:1. 确定聚类数:使用Fisher最优分割算法对时间序列进行聚类,需要先确定聚类数。
可以通过交叉验证等方法来选择最优的聚类数。
2. 建立Fisher矩阵:使用MATLAB中的Fisher矩阵函数可以快速计算出Fisher矩阵。
Fisher 矩阵是一个方阵,其中每个元素表示两个变量之间的相关性。
可以使用以下代码来计算Fisher矩阵:定义时间序列数据data = [1 2 3 4 5; 6 7 8 9 10; 11 12 13 14 15];计算Fisher矩阵F = fisher(data, 'Distance', 'euclidean');在这个示例中,我们使用Fisher函数计算Fisher矩阵,并将'euclidean'作为距离度量方式。
3. 计算最优分割点:使用MATLAB中的fminsearch()函数可以找到Fisher矩阵的最小值。
可以使用以下代码来计算最优分割点:定义最小值搜索函数fun = (x) -sum(x.*F);计算最小值x0 = [0.5 0.5];x = fminsearch(fun, x0);输出最优分割点disp(['最优分割点为:', num2str(x(1)) ', ', num2str(x(2))]);在这个示例中,我们将Fisher矩阵作为输入,并使用fminsearch()函数找到Fisher矩阵的最小值。
最终,我们将得到最优分割点,并将其打印出来。
4. 对时间序列进行聚类:使用MATLAB中的cluster()函数可以将时间序列聚类到相应的聚类中。
可以使用以下代码来进行聚类:定义聚类函数clustFunc = (x) cluster(x, x(1), x(2));对时间序列进行聚类clustLabels = cluster(data, x(1), x(2));输出聚类标签disp(['时间序列的聚类标签为:', num2str(clustLabels)]);在这个示例中,我们将时间序列数据和最优分割点作为输入,并使用cluster()函数将时间序列聚类到相应的聚类中。
Fisher线性分类器通俗解释及MATLAB、Python实现

Fisher线性分类器通俗解释及MATLAB、Python实现⼀、通俗的解释:问题提出:还是以iris的数据为例,有A、B、C三种花,每⼀类的特征都⽤4维特征向量表⽰。
现在已知⼀个特征向量,要求对应的类别,⽽我们⼈可以直接通过眼睛看⽽作出分类的是在⼀维⼆维三维空间,⽽不适应这样的四维数据。
启⽰:假设有这样的⼀个⽅向向量,其与特征向量进⾏内积运算(即向⽅向向量的投影)后,结果为⼀个数值,若同类的特征向量投影后聚集在⼀起,不同类的特征投影后相对分散,那么,我们的⽬的就达到了。
⽬标:这样就有了⽅向,即要寻找⼀个独特的⽅向,使其达到我们的要求。
注:具体的推导过程,参看教科书,另外,在求解极值的时候,利⽤了矩阵论中的向量导数运算。
⼆、MATLAB程序:clearA=[5.1,3.5,1.4,0.24.9,3.0,1.4,0.24.7,3.2,1.3,0.24.6,3.1,1.5,0.25.0,3.6,1.4,0.25.4,3.9,1.7,0.44.6,3.4,1.4,0.35.0,3.4,1.5,0.24.4,2.9,1.4,0.24.9,3.1,1.5,0.15.4,3.7,1.5,0.24.8,3.4,1.6,0.24.8,3.0,1.4,0.14.3,3.0,1.1,0.15.8,4.0,1.2,0.25.7,4.4,1.5,0.45.4,3.9,1.3,0.45.1,3.5,1.4,0.35.7,3.8,1.7,0.35.1,3.8,1.5,0.35.4,3.4,1.7,0.25.2,4.1,1.5,0.15.5,4.2,1.4,0.24.9,3.1,1.5,0.15.0,3.2,1.2,0.25.5,3.5,1.3,0.24.4,3.2,1.3,0.25.0,3.5,1.6,0.6 5.1,3.8,1.9,0.44.8,3.0,1.4,0.35.1,3.8,1.6,0.24.6,3.2,1.4,0.25.3,3.7,1.5,0.2 5.0,3.3,1.4,0.2 7.0,3.2,4.7,1.4];B=[6.4,3.2,4.5,1.5 6.9,3.1,4.9,1.55.5,2.3,4.0,1.36.5,2.8,4.6,1.55.7,2.8,4.5,1.36.3,3.3,4.7,1.6 4.9,2.4,3.3,1.0 6.6,2.9,4.6,1.3 5.2,2.7,3.9,1.4 5.0,2.0,3.5,1.05.9,3.0,4.2,1.56.0,2.2,4.0,1.0 6.1,2.9,4.7,1.45.6,2.9,3.6,1.36.7,3.1,4.4,1.4 5.6,3.0,4.5,1.55.8,2.7,4.1,1.06.2,2.2,4.5,1.5 5.6,2.5,3.9,1.15.9,3.2,4.8,1.86.1,2.8,4.0,1.3 6.3,2.5,4.9,1.5 6.1,2.8,4.7,1.25.5,2.4,3.8,1.1 5.5,2.4,3.7,1.05.8,2.7,3.9,1.26.0,2.7,5.1,1.65.4,3.0,4.5,1.56.0,3.4,4.5,1.6 6.7,3.1,4.7,1.5 6.3,2.3,4.4,1.3 5.6,3.0,4.1,1.3 5.5,2.5,4.0,1.35.5,2.6,4.4,1.26.1,3.0,4.6,1.4 5.8,2.6,4.0,1.2 5.0,2.3,3.3,1.0 5.6,2.7,4.2,1.3 5.7,3.0,4.2,1.25.7,2.9,4.2,1.36.2,2.9,4.3,1.3 5.1,2.5,3.0,1.1 5.7,2.8,4.1,1.3];C=[6.3,3.3,6.0,2.5 5.8,2.7,5.1,1.9 7.1,3.0,5.9,2.1 6.3,2.9,5.6,1.86.5,3.0,5.8,2.27.6,3.0,6.6,2.1 4.9,2.5,4.5,1.7 7.3,2.9,6.3,1.86.7,2.5,5.8,1.87.2,3.6,6.1,2.5 6.5,3.2,5.1,2.0 6.4,2.7,5.3,1.97.7,2.6,6.9,2.36.0,2.2,5.0,1.56.9,3.2,5.7,2.35.6,2.8,4.9,2.07.7,2.8,6.7,2.06.3,3.4,5.6,2.46.4,3.1,5.5,1.86.0,3.0,4.8,1.86.9,3.1,5.4,2.16.7,3.1,5.6,2.46.9,3.1,5.1,2.35.8,2.7,5.1,1.96.8,3.2,5.9,2.36.7,3.3,5.7,2.56.7,3.0,5.2,2.36.3,2.5,5.0,1.96.5,3.0,5.2,2.06.2,3.4,5.4,2.35.9,3.0,5.1,1.8];%⽅法⼀:先将A作为⼀类,BC作为⼀类NA=size(A,1);NB=size(B,1);NC=size(C,1);A_train=A(1:floor(NA/2),:);%训练数据取1/2(或者1/3,3/4,1/4)B_train=B(1:floor(NB/2),:);C_train=C(1:floor(NC/2),:);A_test=A((floor(NA/2)+1):end,:);B_test=B((floor(NB/2)+1):end,:);C_test=C((floor(NC/2)+1):end,:);A_train=A_train;D_train=[B_train;C_train];A_test=A_test;D_test=[B_test;C_test];for i=1:size(A_train,1)S1=S1+(A_train(i,:)-u1)'*(A_train(i,:)-u1);endfor i=1:size(D_train,1)S2=S2+(D_train(i,:)-u2)'*(D_train(i,:)-u2);endSw=S1+S2;w1=(inv(Sw)*(u1-u2)')';w1=w1./norm(w1);y0=w1*(u1+u2)'/2;% a1=w*u1'% d1=w*u2'r1=0;for i=1:size(D_test,1)if w1*D_test(i,:)'<y0r1=r1+1;endendrate_D=r1/size(D_test,1)r2=0;for i=1:size(A_test,1)if w1*A_test(i,:)'>y0r2=r2+1;endendrate_A=r2/size(A_test,1)三、Python程序:from sklearn import discriminant_analysisfrom sklearn.model_selection import train_test_splitimport numpydata = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(0,1,2,3)) target = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(4), dtype=str) t = numpy.zeros(len(target))t[target == 'setosa'] = 1t[target == 'versicolor'] = 2t[target == 'virginica'] = 3#print(clf.predict([data[3]]))。
费舍变换 matlab

费舍变换 matlab费舍变换(Fisher's linear discriminant analysis)是一种经典的监督学习算法,用于特征提取和数据降维。
在MATLAB中,你可以使用`fitcdiscr`函数来实现费舍变换。
这个函数可以用于训练一个线性判别分析器,并且返回一个分类器对象。
你可以使用这个分类器对象来进行预测和特征提取。
下面是一个简单的示例代码,演示如何在MATLAB中使用`fitcdiscr`函数进行费舍变换:matlab.% 生成一些示例数据。
X = [randn(100,2); randn(100,2)+2];Y = [ones(100,1); 2ones(100,1)];% 使用fitcdiscr函数训练一个线性判别分析器。
classifier = fitcdiscr(X, Y);% 使用训练好的分类器对象进行预测。
predictedY = predict(classifier, X);% 获取费舍变换后的特征。
transformedX = X classifier.Coeffs(1, 2).Linear; % 可视化原始数据和变换后的数据。
figure;scatter(X(:,1), X(:,2), 20, Y, 'filled');title('Original Data');xlabel('Feature 1');ylabel('Feature 2');figure;scatter(transformedX, zeros(length(transformedX),1), 20, Y, 'filled');title('Transformed Data');xlabel('Transformed Feature');在这个示例中,我们首先生成了一些示例数据,然后使用`fitcdiscr`函数训练了一个线性判别分析器。
FISHER线性判别MATLAB实现

Fisher 线性判别上机实验报告班级: 学号: 姓名:一.算法描述Fisher 线性判别分析的基本思想:选择一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起,不同类的样本相隔尽可能地远。
Fisher 线性判别分析,就是通过给定的训练数据,确定投影方向W 和阈值w0, 即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
线性判别函数的一般形式可表示成0)(w X W X g T += 其中Fisher 选择投影方向W 的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求。
如下为具体步骤:(1)W 的确定w S 样本类间离散度矩阵b在投影后的一维空间中,各类样本均值Tiim '= Wm样本类内离散度和总类内离散度 T Ti i ww S ' = W S W S ' = W S W 样本类间离散度Tbb S ' = W S W Fisher 准则函数为 max 2221221~~)~~()(S S m m W J F +-=(2)阈值的确定w 0是个常数,称为阈值权,对于两类问题的线性分类器可以采用下属决策规则: 令)()()(21x x x g g g -=则:如果g(x)>0,则决策w x 1∈;如果g(x)<0,则决策w x 2∈;如果g(x)=0,则可将x 任意分到某一类,或拒绝。
(3)Fisher 线性判别的决策规则 Fisher 准则函数满足两个性质:1.投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
2.投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出W :-1w 12W = S (m - m ) 。
这就是Fisher 判别准则下的最优投影方向。
fisheriris数据集matlab中knn分类 -回复

fisheriris数据集matlab中knn分类-回复问题,解释清楚fisheriris数据集是什么,并讲述如何使用knn算法对其进行分类。
首先,我们需要了解fisheriris数据集。
fisheriris数据集是由英国统计学家罗纳德·费舍尔(R.A. Fisher)在1936年提出的一个用于多变量分析和模式识别的经典数据集。
该数据集包含了150个样本,分为3个不同种类的鸢尾花(iris),每个种类50个样本。
每个样本都包含了鸢尾花的4个特征(sepal length、sepal width、petal length和petal width)的测量值。
为了更好地理解数据集,我们可以先进行数据可视化。
在MATLAB中,我们可以使用plot函数来显示样本的特征值。
首先,我们需要将特征值和鸢尾花的类别进行分组,然后使用不同的颜色和符号来表示不同的种类。
以下是可视化代码:load fisheririsgscatter(meas(:,3), meas(:,4), species,'rgb','osd');执行以上代码,我们可以得到一个散点图,其中X轴代表鸢尾花的petallength特征,Y轴代表鸢尾花的petal width特征,不同的颜色和符号代表不同的鸢尾花种类。
通过这个散点图,我们可以观察到不同种类的鸢尾花在特征空间中的分布和重叠情况。
接下来,我们将使用knn算法对fisheriris数据集进行分类。
knn算法是一种基于邻居的分类算法,它的基本思想是将未知样本分类为其k个最近邻居的多数类别。
在MATLAB中,我们可以使用ClassificationKNN对象来实现knn分类器。
以下是knn分类代码示例:load fisheririsX = meas(:,3:4);Y = species;knnModel = fitcknn(X,Y,'NumNeighbors',5);CVKnnModel = crossval(knnModel);classLoss = kfoldLoss(CVKnnModel);以上代码中,我们首先将鸢尾花的petal length和petal width特征值存储在X矩阵中,将鸢尾花的种类存储在Y向量中。
Fisher分类器(算法及程序)
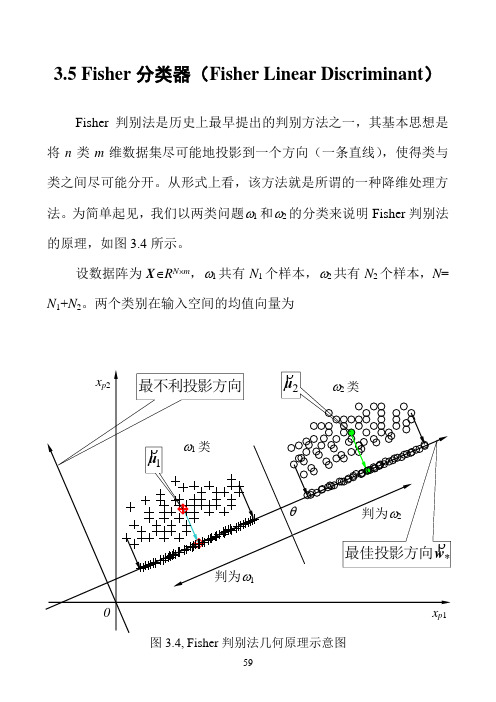
3.5 Fisher分类器(Fisher Linear Discriminant)Fisher判别法是历史上最早提出的判别方法之一,其基本思想是将n类m维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题ω1和ω2的分类来说明Fisher判别法的原理,如图3.4所示。
设数据阵为X∈R N⨯m,ω1共有N1个样本,ω2共有N2个样本,N= N1+N2。
两个类别在输入空间的均值向量为图3.4, Fisher判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μρρρρρρ设有一个投影方向()mT m R w w w ∈=,,,21Λρw ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μρρρρρρρρρρρρ在w ρ方向,两均值之差为())39.3(~~2121μμw μμρρρρρ-=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μρρρρρ定义类间散度(Between-class scatter)平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμρρρρρρρρρρρρρρρρρρρρρρρρρρB T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS ρρρρρρρρρρρρ定义类ωj 的类内散度(Within-class scatter)平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw ρρρρρρρ两个类的总的类内散度误差平方和为()()())44.3(2121221wS w w μμw μw w ρρρρρρρρρρρρW T j Np T jp j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS ρρρρ我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w w ρρρρρW T B T WBSS SS J ==图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义。
fisheriris数据集matlab分类(一)

fisheriris数据集matlab分类(一)Fisheriris数据集MATLAB分类介绍Fisheriris数据集是机器学习中常用的经典数据集之一,由英国统计学家Ronald Fisher提供。
该数据集包含了150个鸢尾花的观测样本,每个样本包含4个特征:花萼长度、花萼宽度、花瓣长度和花瓣宽度。
这些样本被分为了三个类别:Setosa、Versicolor和Virginica。
本文将利用MATLAB对该数据集进行分类分析。
分类方法1. 决策树分类决策树是一种常用的分类方法。
它通过构建一棵树来进行分类决策。
决策树的每个节点代表一个属性,通过划分属性的不同取值来分割样本。
在MATLAB中,可以使用fitctree函数构建决策树分类器,使用predict函数进行预测。
2. 支持向量机分类支持向量机是一种常用的线性分类方法,通过构建一个超平面来划分样本。
在MATLAB中,可以使用fitcsvm函数构建支持向量机分类器,使用predict函数进行预测。
3. 朴素贝叶斯分类朴素贝叶斯是一种基于概率的分类方法,它假设各个特征之间相互独立。
在MATLAB中,可以使用fitcnb函数构建朴素贝叶斯分类器,使用predict函数进行预测。
4. K近邻分类K近邻是一种非参数的分类方法,它通过用样本的最近邻样本进行投票来进行分类。
在MATLAB中,可以使用fitcknn函数构建K近邻分类器,使用predict函数进行预测。
5. 随机森林分类随机森林是一种基于决策树的集成学习方法,它通过构建多棵决策树来进行分类。
在MATLAB中,可以使用TreeBagger函数构建随机森林分类器,使用predict函数进行预测。
结论通过对Fisheriris数据集使用不同的分类方法进行分类分析,我们可以得到不同的分类结果。
不同的方法适用于不同的场景。
决策树分类方法简单直观,适用于特征较少、样本量较小的情况;支持向量机分类方法适用于线性可分的情况;朴素贝叶斯分类方法适用于高维特征的情况;K近邻分类方法适用于数据分布较为均匀的情况;随机森林分类方法适用于特征较多、样本量较大的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fisher 判别法讲解以及matlab 代码实现
两类的线形判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。
过这个预置点且与投影方向垂直的超平面就是两类的分类面。
第一个问题,如何确定投影方向?
这里只讨论两类分类的问题.训练样本集是X ={x1,x2...xn},每个样本是一个d 维
向量,其中第一类w1={11x ,12x ...11n x },第二类w2={21x
,2
2x ...22n x }。
我们
要寻求一个投影方向w (w 也是一个d 维向量),投影以后样本变成:i y =i T
x w (y
是一个标量),i=1...n
在原样本空间中,类均值为:
∑∈=
i
j w x j i
i x
n m 1
i=1,2(一共两类的均值)
(ps.i
m 是一个d*1的矩阵,假设每个维度是一个变量值,mi 中的每一维度就
是这些变量值的均值,如下图所示
:
图1
特别注明:有些例子给的矩阵是这样的:
图2
这里的单个样本是1*d 的矩阵,要注意计算的时候将其转置,不然套用fisher 算法公式的时候就会发现最后得到的矩阵维数不对。
定义各类类内的离散度矩阵为:(类内离散度矩阵其实就是类协方差矩阵,类在多于一个样本,且样本维度>1时是一个矩阵)
∑∈--=
i
j w x T
i
j i j i m x m x S ))((
(因为,
j
x 是一个d*1的矩阵,也可称作d 维向量,
i
m 也是一个d*1的矩阵,
所以最后得到的i
S 一定是一个d*d 的矩阵)
(在用matlab 计算的时候直接用cov (wi )即可得到想要的协方差矩阵,故直接
计算不探究细节时图2可直接cov 算协方差,不用根据公式转置来转置去,不过matlab 中算的协方差被缩小了(n1-1)倍,计算时i
S =cov (w1)*(n1-1))
总的类内离散度矩阵:
21S S S w +=
类间离散度矩阵定义为:
T b m m m m S ))((2121--=
在投影以后的一维空间里,两类的均值分别是;
i
T
w x j T
i
w y i i
ii m w x w
N y N m i
j i j ===
∑∑∈∈1
1 i=1,2
故类内离散度不再是一个矩阵,而是一个值
∑∈-=
i
j w y ii
i ii m y S 2)( i=1,2
总类内离散度为:
1111S S S ww +=
类间离散度:
2
1111)
(m m S bb -=
要使得需求的方向投影能在投影后两类能尽可能的分开,而各类内部又尽可能的
聚集,可表示成如下准则,即fisher 准则:
ww
bb
S S w J =
)(max
将公式代入并通过拉格朗日求极值的方法,可得投影方向:
)(211
m m S w w -=-
(w 是一个d*1的矩阵,或者说亦是一个d 维向量) 阈值可表示为:
)(2
1
22110m m w +-=
最后将待确定样本代入
0)(w x w x g T +=
判断)(x g 的符号和哪个类相同,确定其属于哪个类别。
例子(注意表格中所给的样本维度和公式中变量维度的问题) 代码已经运行无误
代码:
%读取excel中特定单元格的数据
w12=xlsread('E:\模式识别\理论学习\胃病分类问题.xls','C2:F16');
%分别选取类1和类2、测试样本的数据
w1=w12(1:5,:);
w2=w12(6:12,:);
sample=w12(13:15,:);
%计算类1和类2的样本数
r1=size(w1,1);
r2=size(w2,1);
r3=size(sample,1);
%计算类1和类2的均值(矩阵)
m1=mean(w1);
m2=mean(w2);
%各类类内离散度矩阵(协方差矩阵)
s1=cov(w1)*(r1-1);
s2=cov(w2)*(r2-1);
%总类内离散度矩阵
sw=s1+s2;
%投影向量的计算公式
w=inv(sw)*(m1-m2)';
%计算投影后的一位空间内,各类的均值
y1=w'*m1';
y2=w'*m2';
%计算阈值
w0=-1/2*(y1+y2);
%和类相同符号被归为同类
for i=1:r3
y(i)=sample(i,:)*w+w0;
if y(i)*(w'*w1(1,:)'+w0)>0
y(i)=1;
else
y(i)=2;
end
End
判断得出第一个待测样本属于类1,第二,三个待测样本属于类2
如果想进一步知道样本矩阵是如何转置得到最后结果的,可看下面这个例子,这个例子没有用到matlab内置的cov协方差函数(用cov可以直接用样本数据直接进行矩阵运算,不用转置成样本维度向量),所以要进行转置后代入fisher准则公式求解.
x=xlsread('E:\模式识别\理论学习\污染水域问题.xls','C3:F14'); x1=x(1:5,:)';
x2=x(6:10,:)';
sample=x(11:12,:)';
m1=zeros(size(x1,1),1);
% 求类内离散度矩阵
m1=mean(x1,2)
m2=mean(x2,2)
% 求类内离散度矩阵
s1=zeros(size(x1,1),size(x1,1));
for i=1:size(x1,2)
s1=s1+(x1(:,i)-m1)*(x1(:,i)-m1)';
end
s2=zeros(size(x2,1),size(x2,1));
for i=1:size(x2,2)
s2=s2+(x2(:,i)-m2)*(x2(:,i)-m2)';
end
sw=s1+s2;
w=inv(sw)*(m1-m2);
y1=w'*m1;
y2=w'*m2;
w0=-1/2*(y1+y2);
for i=1:size(sample,2)
y(i)=w'*sample(:,i);
if y(i)+w0>0
y(i)=1;
else
y(i)=2;
end
end。
