惯性力
惯性力
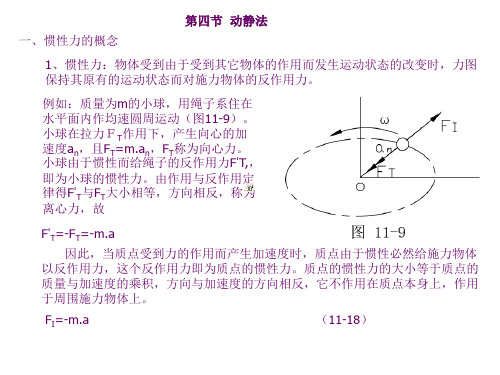
二,动静法 设一质量为m的质点M,在主动力F和约束反力FN作用下沿AB弧运动,其加速度 为a,根据动力学方程有: F+FN=ma 所以 F+FN-ma=0 由(11-18)有 F+FN+ FI =0 (11-19)
上式表明:在质点 运动的任一瞬时,作用 在质点上的主动力,约 束反力与虚加在质点上惯性 力,在形式上组成一平衡力系,这种处理动力学问题的方法称为动静法. 动静法只是一种处理动力学问题的方法.实际上质点并没有受到惯性力作用, 因此质点的这种平衡是虚拟的.我们只是把惯性力虚加在质点上来把质点的动力学 问题转化为静力学问题来处理.
(b)
联解(a)(b)得:
a=
sin 30 o
f s 30o
f s sin 30o + cos 30o
g = 3.32m / s 2
�
例7 小物块A放在车的斜面上,斜面倾角为30,如图.物块A与斜面的静摩擦系 小物块A放在车的斜面上,斜面倾角为30,如图.物块A 数fs=0.2,若车向左加速运动,问物块不沿斜面下滑的加速度a. =0.2,若车向左加速运动,问物块不沿斜面下滑的加速度a 解:以物块A为研究对象,作出其受力图如图. 其中FI是惯性力.
第四节 动静法 一,惯性力的概念 1,惯性力:物体受到由于受到其它物体的作用而发生运动状态的改变时,力图 保持其原有的运动状态而对施力物体的反作用力. 例如:质量为m的小球,用绳子系住在 水平面内作均速圆周运动(图11-9). 小球在拉力FT作用下,产生向心的加 速度an,且FT=m.an,FT称为向心力. 小球由于惯性而给绳子的反作用力F'T,, 即为小球的惯性力.由作用与反作用定 律得F'T与FT大小相等,方向相反,称为 离心力,故 F'T=-FT=-m.a 因此,当质点受到力的作用而产生加速度时,质点由于惯性必然给施力物体 以反作用力,这个反作用力即为质点的惯性力.质点的惯性力的大小等于质点的 质量与加速度的乘积,方向与加速度的方向相反,它不作用在质点本身上,作用 于周围施力物体上. FI=-m.a (11-18)
第20讲义章惯性力

M IzM z(F Iit) m ir i r i ( m ir i2 ) J z 14
第二十章 惯性力
综上所述,惯性力系向转轴上一点O简化的主矩为
M IOM IxiM IyjM Izk
如果刚体有质量对称平面,切该平面与转轴z垂直,简化中 心O取为 此平面与转轴的交点,则有
F IR P gaCP g(aAaC t )A F Ie F Ir
式中
FIeP gaA,FIrP gaC t A
惯性力系向质心简化得主矩为
M IC
J C
1 12
P l 2
g
1P
12
g
la A
方向如图所示。
B
F Ie C
O
F
t Ir
M IC
q
A aA
21
第二十章 惯性力
再向O点简化, 主矢不变
P F IR g a C
M I O r i ( m i a i ) (m i r i ) a C m r C a C
若选质心C为简化中心,则 rC=0,有: MIC 0
故平移刚体的惯性力系可以简化
为通过质心的合力,其力大小等
于刚体质量与加速度的乘积,合
力的方向与加速度方向相反。
12
第二十章 惯性力
2、定轴转动刚体 如图示定轴转动刚体,考 虑质点i,以O为简化中。 有
29
第二十章 惯性力
由前面所得,即有
F Ix mC a x0, F Iy mC a y0
置静止落下。求开始落下时杆AB的角加速度及A点支座反力。
解: 选杆AB为研究对象
虚加惯性力系:
FIt
ml
2
F Inmna 0,M IAJA m 3 2l
2-3惯性力

巴黎国葬院
傅 科 摆
§3、非惯性系 定义: 一、定义 1. 惯性系 牛顿定律始终成立的参考系 惯性系: 2. 非惯性系: 相对惯性系有加速度的 非惯性系 参照系 加速小车上的小球。 例:加速小车上的小球。 地面观察者: 地面观察者: F=0, a=0 车上观察者: 车上观察者: a F = 0 , = - a0 = 0 牛顿定律不正确。 牛顿定律不正确。
a0
可见, 可见,在非惯性系中必须引进惯性力 F0 = m a0
这时牛顿第二定律为: 这时牛顿第二定律为: F + F 0= m a 注意: 注意 A.惯性力 惯性力的方向与 相反。 A.惯性力的方向与 ao 相反。 B. 惯性力是一个假想的力,而非真实力。 惯性力是一个假想的力,而非真实力。 假想的力 C. 惯性力只有受力物体 而无施力物体。 惯性力只有受力物体 而无施力物体。 只有受力物体,
a0Βιβλιοθήκη 以加速小车为参照系牛顿定律不正确, 以加速小车为参照系牛顿定律不正确, 必须修正。 必须修正。 二、惯性力 F0 = a0 m a0 非惯性系相对于惯性系的加速度 非惯性系中的牛顿定律形式: 则:非惯性系中的牛顿定律形式: F + F 0= m a F a 真实力 F0 惯性力 物体相对于非惯性系的加速度
0.
0.
图1
图2
*:惯性离心力 : 人随车转弯时,车为非惯性系 例:人随车转弯时,车为非惯性系 人受惯性力的作用 且:F0 = - Fn = - man 惯性力F 的方向a 的方向相反, 惯性力F0的方向 n的方向相反, 径向向外,为惯性离心力。 径向向外,为惯性离心力。
ω
Fn m F0
一单摆. 当小球摆至最高位置时; [ 例1 ] 一单摆.(1)当小球摆至最高位置时; 释放框架自由下落,如图1 释放框架自由下落,如图1、问小球相对于框 当小球摆至平衡位置时, 架如何运动 ?(2)当小球摆至平衡位置时,释 放框架,如图2 小球相对于框架如何运动? 放框架,如图2,小球相对于框架如何运动?
惯性力

夏季强热带风暴的漩涡
表现(观)重力 representation weight 地球上测得的物体的重力是表现 重力。表现重力是万有引力 P与惯性离 心力 f 的合力。显然这一合力 P 与纬 度值有关。 重力加速度
2 2 g 2 a引 a离 2a引a离 sinq
g a
引
q
a
a引 a离 g a引 a离 sinq
g北极=9.832 m/s2
离
已考虑惯性离心力在内
潮汐 tide 涨潮,落潮是海水受太阳和月亮引力及地球这个非惯性 系中的惯性力共同作用的结果。 以太阳的作用为例,解释这一现象。 地球绕太阳公转,考虑地心这个平动加速参考系。 地心O处,质点受太阳引力 F 与惯性力 f ,
★ 你把不论什么东西 扔给你的同伴时, 如果 你的同伴在船头而你在 船尾, 你所用的力并不 比你们两个站在相反位 置时所用的力更大.
伽利略实验
★ 水滴将象先前一样, 滴进下面的罐子, 一滴 也不会滴向船尾, 虽然 水滴在空中时, 船已行 驶了相当距离.
非惯性系 惯性力
• 一、非惯性系 noninertial system • 惯性定律不成立的参考系(相对于惯性系作加速运动)。 • 二、惯性力 inertial force • 在非惯性系中,牛顿运动定律不适用,但是也可以假想, 在非惯性系中,除了物体相互作用所引起的力以外,还有一种 由于非惯性系而引起的力——惯性力,这样就能在形式上运用 牛顿运动定律了。 惯性力没有真正施力者,所以也就没有反作 用力。 三、平动参考系 flat movement
什么是惯性力有何表现

什么是惯性力有何表现关键信息项:1、惯性力的定义2、惯性力的表现形式3、惯性力与惯性的区别4、惯性力在不同场景中的作用5、惯性力对物体运动的影响6、如何理解和计算惯性力11 惯性力的定义惯性力是在非惯性参考系中,为了使牛顿运动定律在形式上仍然成立而引入的一种假想力。
在惯性参考系中,物体的运动遵循牛顿第一定律和牛顿第二定律,即物体在不受外力或所受合外力为零时保持静止或匀速直线运动,所受合外力不为零时产生加速度。
然而,在非惯性参考系中,由于参考系本身具有加速度,物体的运动看起来不符合牛顿定律,此时引入惯性力来修正这种偏差。
111 惯性力的特点惯性力不是由物体之间的相互作用产生的,而是由于参考系的加速运动导致的。
它没有施力物体,也不能通过牛顿第三定律找到其反作用力。
112 惯性力的大小和方向惯性力的大小等于物体的质量乘以参考系的加速度,方向与参考系的加速度方向相反。
12 惯性力的表现形式121 直线加速运动中的惯性力当参考系沿直线加速运动时,物体受到的惯性力沿相反方向。
例如,在一辆加速前进的汽车中,乘客会感觉到身体被向后推,这个向后的力就是惯性力。
122 旋转运动中的惯性力在旋转参考系中,会出现离心力和科里奥利力等惯性力。
离心力使物体远离旋转中心,而科里奥利力则会改变物体在旋转参考系中的运动方向。
123 复杂运动中的惯性力组合在实际情况中,参考系的运动可能是多种形式的组合,此时惯性力也会相应地组合和叠加。
13 惯性力与惯性的区别131 惯性是物体保持原有运动状态的性质,是物体的固有属性,与参考系的选择无关。
而惯性力只在非惯性参考系中存在,是为了描述物体在非惯性系中的运动而引入的概念。
132 惯性的大小由物体的质量决定,质量越大,惯性越大。
惯性力的大小则取决于参考系的加速度和物体的质量。
14 惯性力在不同场景中的作用141 在工程和技术中的应用例如,在设计离心分离设备、游乐场的旋转游乐设施等时,需要考虑惯性力的作用来确保安全和正常运行。
惯性力和惯性的大小

惯性力和惯性的大小众所周知,物理学中有惯性的概念,惯性力的概念;而且惯性是有大小的,惯性力是不存在的。
笔者在长期的教学研究中发现,认为惯性有大小是不合理的,惯性力也未必是一种假想的力,它很可能是一种客观存在。
博士论文,惯性。
1•惯性力的概念惯性1. 1惯性力的原始概念大家知道:牛顿定律只适用于惯性系而不适用于非惯性系。
例如在由静止加速前进的火车上,受合力为零的小球会相对于火车向后加速运动。
为了使牛顿运动定律在火车中同样成立,需要引入惯性力的概念,所引入的惯性力大小,其方向与火车的加速度方向反向。
这样就有牛顿第二定律得以成立。
也就是说:相对于地面(我们认为是惯性系)有加速度的参照系是非惯性系,非惯性系中牛顿运动定律不成立,欲使牛顿运动定律成立,需要引入惯性力。
正是在这些问题中,我们认识了什么是惯性力。
然而本文所要定义的惯性力与上述惯性力的概念是完全不同的。
1. 2惯性力的新定义我始终有这样一个猜想:“所有物质组成的宇宙具有这样的一种性质,它可以允许任何物体对其保持原有的运动状态,而不允许任何物体对其有加速度;如果物体对宇宙有加速度,物体就会受到宇宙对它的一种约束力,这种力就是我所定义的惯性力。
即惯性力是宇宙对物体的一种约束力,它并不是假想的力,是一种真实作用力。
”[需要说明的是,我这里所说的惯性力只是真正的惯性力在我们所能看到的参考系中的分力,而真正的属性力我们是无法知道的,因为我们不可能知道绝对的加速度。
以上这段文字在英语稿中没有]惯性力的施力物体是宇宙,就好象重力的施力物体是地球一样。
宇宙中的一切物体只要对宇宙有加速度,就一定受到惯性力。
惯性力的大小与其相对于惯性系的加速度成正比,与相对于惯性系的加速度的方向相反。
如果物体的质量为m,对惯性系的加速度为a,则惯性力的大小为f=ma。
显然惯性力是非平衡状态下才受到的一种力。
关于惯性力的产生机理,我猜想应该类似于变化的电场产生磁场。
当然这仅仅是一种猜想,有待于实验的验证。
惯性与惯性力对物体运动的影响

惯性与惯性力对物体运动的影响惯性和惯性力是物理学中的基本概念,它们在解释和描述物体运动方面起着重要的作用。
惯性是物体保持自身运动状态的性质,而惯性力则是由于物体惯性产生的力。
本文将探讨惯性和惯性力对物体运动的影响,并分析其背后的物理原理。
在我们日常生活中,我们常常会观察到物体的运动状态是多种多样的。
有些物体保持静止,有些物体做直线运动,还有些物体做曲线运动。
这是由于物体本身具有惯性导致的。
惯性的基本原理是根据牛顿第一定律,即一个物体如果没有受到外力作用,就会保持静止或匀速直线运动的状态。
当我们对一个静止的物体施加一个力后,它会发生变化。
这是因为物体在受到外力作用后,会产生一个反作用力,这个反作用力就是惯性力。
惯性力的大小和方向与外力大小和方向相等但相反。
想象一下,当我们用力推一个书桌时,书桌会有一个相反方向的反作用力作用在我们身上,这便是惯性力的体现。
惯性和惯性力对物体的运动状态有着重要的影响。
首先是物体保持静止或直线匀速运动的性质。
在没有外力作用的情况下,物体会保持其运动状态不变。
这解释了为什么地球公转、宇宙飞船在太空中直线匀速运动等现象。
物体的惯性使它们能够保持稳定的运动状态,不会发生任意的改变。
其次,惯性和惯性力还可以解释物体做曲线运动的原因。
当我们用手持物体绕圆周运动时,物体会产生离心力与我们的手相反方向的惯性力。
这个惯性力使得物体有向外的趋势,垂直于它的切线方向。
这一原理可以用来解释为什么车辆在转弯时会有向外的离心力作用于人们身上。
惯性和惯性力的概念和机制在众多领域都得到了应用。
在工程学中,惯性力的概念被广泛应用于设计坐船、飞机和汽车等交通工具。
通过考虑惯性力对乘客的影响,可以确保乘坐的稳定性和舒适性。
在运动学和动力学中,惯性和惯性力是解释和计算物体运动和受力的基础。
尽管惯性和惯性力在物体运动中起到重要作用,但在某些情况下,它们也会对物体运动造成不利影响。
例如,在突然变化的力作用下,物体的惯性导致它们继续运动的惯性条件,从而可能导致损坏或伤害。
基本物理学问题中的惯性力和惯性质量

基本物理学问题中的惯性力和惯性质量一、引言惯性力和惯性质量是基础物理学中的重要概念,它们在描述物体运动时具有至关重要的作用。
这两个概念在物理学中的地位,类似于数学中的基本运算符号,是基本、必不可少的。
二、惯性力在描述物体运动时,有时候会遇到力的作用方向与物体方向不一致的情况。
这时候就需要引入惯性力。
惯性力是物体由于其惯性而产生的一种力,这种力与物体运动的状态有关。
比如,当我们在车上突然刹车时,我们的身体会向前倾,这是因为我们的身体具有惯性。
当车突然停止,身体仍然具有向前的惯性,导致身体向前倾。
这时,我们会感觉到一个向后的推力,这就是惯性力。
惯性力的大小与物体的质量、加速度以及惯性系的参考系有关。
在不同的参考系下,一个物体所受的惯性力是不同的。
三、惯性质量惯性质量是用来衡量物体惯性大小的物理量。
它描述了物体对力的反应能力,也就是说,物体的惯性越大,它所能受到的力也就越大,这就是惯性质量和力的关系。
惯性质量与物体的质量密切相关,但并不完全相同。
惯性质量是描述物体惯性大小的一个物理量,而物体的质量描述的是它的质量大小。
比如,一个小石头和一个大石头在相同的力作用下,根据牛顿第二定律,它们所受到的加速度应该是不同的。
这是因为它们具有不同的惯性质量。
尽管它们的质量相同,但是惯性质量不同,因此所受到的力也不同。
四、结论惯性力和惯性质量是描述物体运动时必不可少的概念。
惯性力描述了物体由于惯性而产生的一种力,而惯性质量则描述了物体对力的反应能力。
在实际中,我们常常需要考虑惯性力和惯性质量对物体运动的影响,在设计机器、运动模拟等方面,有重要的应用价值。
哲学家牛津在《人性困境》中指出:我们感知的世界,总是是以惯性的形式出现的。
这一点在物理学中也同样有体现。
物体的惯性力和惯性质量,是我们理解物体运动时必须要了解的重要概念,同时也是深入理解物理学的关键之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浅谈惯性力
在物理学中,大多数的力都有施力物体。
然而惯性力却不然,惯性力是没有施力物体的力。
它是为了满足牛顿运动定律在非惯性系中的数学表达形式不变而引入的。
惯性力是指当物体加速的时候,惯性会使物体保持原有的运动状态的倾向,若是以该物体为参照物,看起来仿佛有一股方向相反的力作用在该物体上,因此成为惯性力。
因为惯性力实际上并不存在,实际存在的只有原本将该物体加速的力,所以惯性力又称假象力。
形象的体现了惯性力的不存在性。
例如我们在乘公车的时候有一个明显的体会就是,当司机忽然加速的时候,我们的身体会向后倾,有时甚至会因为一些人的没扶好支撑物而跌倒。
这时,人们就会想,我们向前后倾是因为什么物体给我们了一个力呢?实际上这里根本不存在一个将我们向后推动的力,这只是惯性在不同参照系下的表现而已。
当汽车加速运动时,地面上的人看到汽车里面的人是运动的且加速度和汽车加速度是一样的。
但是汽车里面的人看到与他们一起乘车的人却是静止不动的。
如果我们对人进行受力分析,那么人受到重力和支持力。
这两个力是平衡的。
根据牛顿运动定律,人是不会移动的,但是人确实又移动了。
这就是牛顿力学的一个局限。
为了拟补这个缺陷,我们引入了惯性力这个概念。
在处于非惯性系中的物体上人为的加上一个与该非惯性系数相等,方向相反的加速度。
因为这个加速度是由于惯性引起的,所以将这个加速度的力成为惯性力。
这样就可以解释我们在坐汽车时遇到的现象。
所以惯性是物体本身的性质,不是力。
我们知道对一切运动的描述,都是相对于某个参考系的。
参考系选取的不同,对运动的描述,或者说运动方程的形式,也随之不同。
人类从经验中发现,总可以找到这样的参考系:其时间是均匀流逝的,空间是均匀和各向同性的;在这样的参考系内,描述运动的方程有着最简单的形式。
这样的参考系就是惯性参照系,也称为惯性参考系或惯性系。
而非惯性系则是能够对同一个被观测的单元施加作用力的观测参照框架和附加非线性的坐标系的统称。
非惯性参照系的种类无穷多。
在经典机械力学中,任何一个使得“伽利略相对性原理”失效的参照系都是所谓的“非惯性参照系”。
比如,一个加速转动的参照系;一个加速振动的参照系;……;一个随机任意加速运动的参照系等等。
即任何一个使得牛顿第一定律和牛顿第二定律不再成立的参照系。
在经典电动力学中,任何一个使得“爱因斯坦相对性原理”失效的参照系都是所谓的“非惯性参照系”。
比如,任何一个使得洛伦兹电磁作用力定律,或者麦克斯韦方程组不再成立的参照系。
事实上牛顿运动定律只在惯性系中成立,然而在现实中,我们又不得不与非惯性系打交道。
例如在研究大气环流一类大尺度的运动时,自转着的地球就是一个非惯性系,所以转动参考系就是一个非惯性系,在实际中有着非常重要的意义。
物理学家总希望以最简明的方程概括最多的现象。
对于非惯性系,关键在于寻找惯性力的正确表达式,然后把真实力与惯性力的矢量和作为总的力。
这样在非惯性系中质点运动学方程的形式保持不变,因此,牛顿运动学在非惯性系中又可以运
用。
我们通常虽然也说运动是一种相对运动,是相对于参考系说的,但我们认为运动是一个物体的性质,一个物体由于惯性保持速度不变。
外力可以改变这种运动状态。
但我们通常指的运动其实是两个物体的运动差。
我们用运动差表示一个物体的速度。
用参考系与物体的运动差表示为物体的速度或其他。
或说用物体的速度表示两个物体的运动差。
惯性力和电磁力之间的一种有趣的相似性,近来已有所介绍,证明
了在一非惯性转动参照系中的离心力和科里奥利力能够用静电力和
磁力来模拟.。
