“对称反对称原理”和机构惯性力平衡
浅谈“对称性”在高中物理力学问题中的应用

浅谈“对称性”在高中物理力学问题中的应用在物理学中,“对称性”是一个非常重要的概念,它在解决各种力学问题中起着至关重要的作用。
对称性在高中物理课程中占据着重要的地位,它不仅是基础知识的一部分,也是解决问题的关键。
本文将浅谈“对称性”在高中物理力学问题中的应用,通过一些具体的例子,帮助学生更好地理解和应用这一重要概念。
在物理学中,对称性主要包括平移对称、旋转对称和镜像对称。
平移对称是指当系统的性质不随空间的平移而变化时,就说系统具有平移对称性。
旋转对称是指当系统的性质不随空间的旋转而变化时,就说系统具有旋转对称性。
镜像对称是指当系统的性质不随镜像翻转而变化时,就说系统具有镜像对称性。
这些对称性不仅可以用来描述物体的形状,也可以用来研究力学问题中的平衡、稳定等性质。
在力学问题中,对称性的应用是非常多样的。
以平衡问题为例,平衡是一个非常基础且重要的问题,而对称性可以帮助我们简化平衡问题的分析和求解。
在斜面上放置一个物体,斜面具有对称性,它不随平移而变化,因此我们可以利用对称性来简化受力分析,找出物体达到平衡时的条件。
另外一个重要的力学问题是旋转问题。
对称性在旋转问题中同样具有重要作用。
一个实心圆盘绕自身的对称轴旋转,由于盘的形状具有旋转对称性,因此我们可以利用这一对称性来简化刚体的转动惯量、角动量等问题的求解。
对称性还可以帮助我们发现一些物理定律和物理规律。
在牛顿第一、第二定律中,物体的平动和转动方程都是具有对称性的,它们不随时间、空间的平移和旋转而变化。
这些对称性不仅帮助我们理解和推导这些定律,也帮助我们更好地应用这些定律来解决实际问题。
对称性在高中物理力学问题中的应用是非常广泛的。
在解决力学问题时,我们可以通过识别系统的对称性,简化受力分析,找出物体达到平衡的条件,求解刚体的转动惯量和角动量等问题。
对称性也帮助我们理解和推导一些物理定律和规律,是我们更好地掌握力学知识和解决实际问题的重要工具。
通过对对称性的应用,可以帮助学生更好地理解力学问题,提高解题能力。
对称与反对称运动实验设计与分析

实验步骤:设定运动参数、采集数据、 分析数据
实验结果:对称运动与反对称运动的差 异性表现
实验结论:对称运动与反对称运动在生 理和心理上的影响
实验条件:设定实验的环境 和条件
实验对象:选择合适的实验 对象和材料
实验目的:明确实验的目的 和预期结果
实验方法:选择合适的实验 方法和技术
对称与反对称运动实 验设计与分析
汇报人:XX
目录
ห้องสมุดไป่ตู้
添加目录标题
对称与反对称运动 实验原理
对称与反对称运动 实验设计
对称与反对称运动 实验数据分析
对称与反对称运动 实验结果讨论
对称与反对称运动 实验结论总结
添加章节标题
对称与反对称运动 实验原理
对称运动:物体 在运动过程中, 其形状、大小、 质量等物理量保 持不变的运动。
反对称运动:物 体在运动过程中, 其形状、大小、 质量等物理量发 生变化的运动。
对称与反对称运 动的区别:对称 运动中,物体的 物理量保持不变; 反对称运动中, 物体的物理量发 生变化。
对称与反对称运动 的应用:在物理学、 工程学、生物学等 领域,对称与反对 称运动原理被广泛 应用于各种实验设 计和分析中。
操作简单
反对称运动实 验的缺点:结 果准确性较低, 可重复性较差
实验设计:优化实验方案,提高实验效率 数据处理:改进数据处理方法,提高数据准确性 实验结果分析:深入分析实验结果,挖掘实验数据背后的规律 实验改进:根据实验结果和分析,提出改进措施,提高实验效果
感谢您的观看
汇报人:XX
对称与反对称运动 实验设计
实验目的:验证对称运动的原理和特性 实验设备:运动平台、力传感器、数据采集系统等 实验步骤:设定运动参数、启动运动平台、采集数据、分析数据等 实验结果:验证了对称运动的原理和特性,为后续研究提供基础数据
试论大学物理中的“对称性”与力学三大守恒定律的关系

试论大学物理中的“对称性”与力学三大守恒定律的关系作者:赵波来源:《神州·下旬刊》2018年第04期摘要:“对称性”,是物理力学分析中的主要内容,它与物理学中的众多理论都有着密切的联系。
基于此,本文着重对大学物理中“对称性”与力学三大守恒定律的关系进行论述,以达到重新梳理物理学相关知识,实现学科研究知识在归纳中拓展的目的。
关键词:大学物理;“对称性”;力学三大守恒定律引言:随着社会理论分析的视角逐步拓展,人类文明的研究领域也在逐步拓宽。
大学物理,是人类应用现有理性思维知识,实现世界资源、空间分析的直接体现。
大学物理教师在教学过程中,为了对“对称性”进一步解读,将其与力学三大守恒定律结合在一起,全面实现理论知识综合解析。
一、对称与“对称性”之间的关系对称,是在二维平面轴对称的定义上延伸出来的理论,是指处于同一平面中两个平行物体,它们在样式、颜色、空间分布等方面都相同,但其方向却相反的物质。
而对称性,是在对称概念的基础上,延伸出来的形态特征。
如某一物体经过某一个周期旋转后,依旧与原来的图像相互吻合,那么,我们就称物体的这种特征为“对称性”[1]。
“对称性”原理,是牛顿力学原理基础之一。
力学在这一理论之上,引申出物质发展的对称性与不对称的关系,进而对物质守恒的相关原理进行证明论述。
此外,“对称性”的分析,也能够进一步拓展质量、数量层面的延伸,小到一粒微尘的变化,大到世界物质的生存与死亡,均遵循着“对称性”和“非对称性”之间的关系[2]。
二、“对称性”与力学三大守恒定律之间的关系(一)时间平移与能量守恒定律依据力学的能量守恒定律可知:物质中的能量不会凭空产生,也并不会凭空消失,它的运作始终遵循着能力均衡的状态。
而大学物理中提到的“对称性”,也是从这一层面,对时间的运动规律进行总结。
如,我们每天经历的时间均是24小时,每一小时又分为60分钟,每一分钟又被分为60秒。
今天如此,昨天亦如此,未来也如此。
论“对称性”在高中物理力学问题中的效用

������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
知当磁场方 向 竖 直 向 上 时,由 左 手 定 则 可 知 安 培 力 水 平 向
右,金属杆ab 受力可以平衡,A 正确;若 磁 场 方 向 竖 直 向 下, 由左手定则可知安培 力 水 平 向 左,则 金 属 杆 ab 受 力 无 法 平 衡,B、C、D 错误.答案为 A. 四 、力 学 置 换 方 面
的趣味性.因此,在 高 中 物 理 力 学 问 题 解 析 中 引 用 对 称 性,
能够有效降低解题 难 度,帮 助 学 生 构 建 知 识 体 系,使 学 生 能
够灵活应用所学知识去解答问题.从 实 践 效 果 来 看,此能 力 ,提 升 考 试 成 绩 .
石
块
运动到抛出点下方离抛出点15 m 时,位移为x=-15 m,由
x=v0t-
12gt2
代 入 得 -15=20t-
1 2
×10t2,解 得t1 = (2
+ 7)s,t2=(2- 7)s(舍去).故选 ACD. 二 、结 构 力 学 方 面
在教学有关结构力学方面的知识时,此 内 容 对 于 学 生 而
结构力学对称性应用

对称性应用在工程问题中,有很多结构都具有对称性。
我们对这些结构进行受力分析的时候,常常将结构简化为杆系模型,而结构力学研究的就是结构的杆系模型,因此对称性在结构力学中有着广泛的应用。
现在就对称性在结构力学中的应用做一简单的总结。
结构的对称性是指结构的几何形状和支座形式均对称于某一几何轴线。
而荷载的对称则分为正对称荷载和反对称荷载。
另外需要注意的是杆件截面和材料的性质也要对于此轴对称。
在对称荷载作用下,结构内力呈对称分布。
在反对称荷载作用下,结构内力呈反对称分布。
如下图所示:对称性在求解结构内力中的应用:对称结构在正对称荷载作用下,其对称的内力(弯矩和轴力)和位移是正对称的,其反对称的内力(剪力)是反对称的;在反对称荷载作用下,其对称的内力(弯矩和轴力)和位移是反对称的,其反对称的内力(剪力)是正对称的。
因此,只要我们做出半边结构的内力图,也就知道了整个结构的内力图。
据此,我们在对对称结构进行内力分析时,就可以取半边结构进行分析。
取半边结构进行分析,可以减少超静定次数,减少基本未知量,为解题提供了很大的方便。
在用力法解决超静定问题时,对于对称的结构,可利用对称性简化计算。
简化步骤如下:1、选取对称的基本结构。
2、将未知力及荷载分组。
3、取半结构进行计算。
对于对称结构承受一般非对称荷载时,利用荷载分组,将荷载分解为正、反对称的两组,并将他们分别作用于结构上求解内力,然后将计算结果叠加。
反对称正对称在计算对称结构时,根据对称结构特性,可以选取半个结构计算。
选取半结构的原则:1、在对称轴的截面或位于对称轴的节点处2、按原结构的静力和位移条件设置相应的支撑,使半结构与原结构的内力和变形完全等效奇数跨对称结构:偶数跨对称结构:在用位移法求解超静定结构的时候,同样可以利用对称性简化计算。
分析可知,在正对称荷载时用位移法求解只有一个基本未知量;但在反对称荷载时若用位移法求解将有两个基本未知量,而用力法求解则只有一个未知量。
物理学中的对称性原理

物理学中的对称性原理物理学中的对称性原理是指在自然界中存在着各种对称性,并且这些对称性对于物理定律的描述和解释起着重要的作用。
对称性原理是物理学中的基本原理之一,它帮助我们理解和解释了许多重要的现象和规律。
一、空间对称性空间对称性是指物理系统在空间变换下保持不变。
在三维空间中,常见的空间对称性有平移对称性、旋转对称性和镜像对称性。
1. 平移对称性:物理系统在空间平移下保持不变。
例如,一个自由粒子在空间中运动时,其动能和势能在空间平移下保持不变。
2. 旋转对称性:物理系统在空间旋转下保持不变。
例如,一个均匀的圆盘在绕其对称轴旋转时,其物理性质保持不变。
3. 镜像对称性:物理系统在空间镜像变换下保持不变。
例如,一个球在经过镜像变换后,其形状和物理性质保持不变。
二、时间对称性时间对称性是指物理系统在时间反演下保持不变。
时间反演是指将时间t变为-t,即将物理系统的演化方向反转。
时间对称性原理表明,物理定律在时间反演下保持不变。
1. 动力学时间对称性:物理系统的演化方程在时间反演下保持不变。
例如,牛顿第二定律F=ma在时间反演下仍然成立。
2. 热力学时间对称性:热力学系统的热平衡状态在时间反演下保持不变。
例如,一个封闭的热力学系统在达到热平衡后,其热平衡状态在时间反演下保持不变。
三、粒子对称性粒子对称性是指物理系统在粒子变换下保持不变。
粒子变换是指将一个粒子变为另一个粒子,例如将一个电子变为一个中子。
粒子对称性原理表明,物理定律在粒子变换下保持不变。
1. 电荷守恒:电荷在粒子变换下保持守恒。
例如,一个粒子和其反粒子的电荷之和为零。
2. 弱力相互作用:弱力相互作用在粒子变换下保持不变。
例如,一个粒子在弱力相互作用下可以转变为另一种粒子。
四、规范对称性规范对称性是指物理系统在规范变换下保持不变。
规范变换是指改变物理系统的规范场,例如改变电磁场的规范。
规范对称性原理在量子场论中起着重要的作用。
1. 电磁规范对称性:电磁场的规范变换不改变物理系统的物理性质。
解析二 对称结构
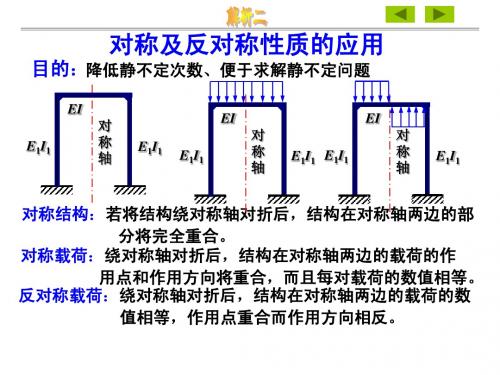
目的:降低静不定次数、 目的:降低静不定次数、便于求解静不定问题
EI E1I1 对 称 轴 E1I1 E1I1 EI 对 称 轴 E1I1 E1I1 EI 对 称 轴 E1I1
对称结构:若将结构绕对称轴对折后,结构在对称轴两边的部 对称结构:若将结构绕对称轴对折后, 分将完全重合。 分将完全重合。 对称载荷:绕对称轴对折后, 对称载荷:绕对称轴对折后,结构在对称轴两边的载荷的作 用点和作用方向将重合,而且每对载荷的数值相等。 用点和作用方向将重合,而且每对载荷的数值相等。 反对称载荷:绕对称轴对折后, 反对称载荷:绕对称轴对折后,结构在对称轴两边的载荷的数 值相等,作用点重合而作用方向相反。 值相等,作用点重合而作用方向相反。
X2 X3 X1 X3 1 X X2
X2
P
X3 X3 X1 X1 X2
P
P
X2
X2
P
对称轴通过的截面处内力特点和变形特点: 对称轴通过的截面处内力特点和变形特点: 内力特点和变形特点
对称载荷: 对称载荷: 剪力为零, 仅有轴力与弯矩, 剪力为零, 仅有轴力与弯矩,且转角及水平位移为零 反对称载荷: 反对称载荷: 轴力及弯矩为零, 仅有剪力, 轴力及弯矩为零 仅有剪力 且垂直位移为零
对称结构 对称载荷
对称结构 反对称载荷
F2
F2
F2
F2
F1
பைடு நூலகம்F1 F1
F1
qq/2 F F/2 F /2 F/2 FF /2 q/2 q/2
对称结构在对称载荷和反对称载荷作用时的变形和内力特点: 对称结构在对称载荷和反对称载荷作用时的变形和内力特点: 变形、 变形、内力关于对称轴对称 对称载荷 反对称载荷 变形、 变形、内力关于对称轴反对称 对称轴通过的截面处内力和变形特点: 内力和变形特点 对称轴通过的截面处内力和变形特点: P P P
CAD绘图中的对称与平衡原理与应用

CAD绘图中的对称与平衡原理与应用在CAD(计算机辅助设计)软件中,对称与平衡是非常重要的设计原则与技巧。
通过灵活应用对称与平衡,可以让我们的绘图作品更加美观、优雅,同时提升其功能性与可读性。
本文将介绍CAD绘图中的对称与平衡原理,并提供一些相关的应用技巧。
对称原理是指将图形的两侧或多个部分以某个中心点、轴线或面进行镜像,使得两侧或多个部分完全一致。
对称可以分为水平对称、垂直对称和轴对称。
水平对称是将图形上下翻转,使得两侧相同;垂直对称是将图形左右翻转,使得两侧相同;轴对称是将图形绕着一个轴线旋转180度,使得两侧相同。
在CAD软件中,实现对称非常简便。
我们可以使用"镜像"命令来进行水平或垂直对称,只需要选择需要对称的对象和镜像线即可。
而轴对称则可以通过"旋转"命令来实现,选择对象和旋转角度为180度即可。
此外,还可以使用"偏移"命令来实现对称,只需选择偏移距离为对象的一半即可。
对称的应用在CAD绘图中非常广泛,无论是绘制物体的外形,还是设置文字的排布,都可以运用对称原理。
例如,在绘制建筑平面图中,我们可以通过对称绘制两侧的房间,以保证布局的平衡与美观。
又如,在设计产品外观时,通过对称可以让产品看起来更加均衡与稳定。
除了对称,平衡原理也是CAD绘图中不可忽视的设计原则。
平衡是指图形的各个部分在空间或视觉上的均衡分布。
平衡可以分为对称平衡和不对称平衡。
对称平衡是指图形的各个部分在绘图板上以某个中心点或轴线为中心均衡分布;不对称平衡则是指图形的各个部分在绘图板上按照一定的比例或分布规律达到均衡。
实现平衡也可以借助CAD软件提供的工具来完成。
我们可以使用"移动"命令来移动需要调整位置的对象,通过调整位置来实现平衡。
另外,还可以利用"伸展"命令来调整某个对象的大小,使其与其他对象在视觉上达到平衡。
平衡的应用范围广泛,不仅可在平面绘图中应用,在三维模型设计中同样重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代流行的提花纺织机高速运行的瓶颈问题 , 是 高
速 往 复运 动的提 刀机 构构 件惯性 力 得不 到很好 的平
纺织机械
2 0 1 4年 第 1 期
・ 研 究与 应 用 ・ 2 9
振动 , 操 作 女 工 开 机后 , 赶 紧跑 开 。原 因很 简 单 , 两
G、 H 铰接 另一 根提 刀 梁 D ; 每件 提 刀 梁 中部 有 铰 链, 分别 为 和 0 4 ; 铰接 两件 滑块 M 、 N, 滑 块 由滑
件 的加 速度 总是数 值 相等 、 方 向相反 , 即 它们 的惯性 力 完全抵 消 了 , 实现 了机构 构件 的惯性 力 完全平 衡 。
“ 在 工程实 际 中 , 机架 所受 的振 动力 和振 动力 矩
完全 平衡 往 往 很 难 实 现 ” , 现 行 采 用 最 多 的是 配 重 法, 一般 只能做 到 “ 综 合 优化平 衡 ” , 适 当地部 分平 衡 主要 影响运 行 效 果 的惯 性 力 和 惯 性 力 矩 。否则 , 机
艺 的要求 。
中一个连杆的下部 , 安装了一对外啮合圆柱直齿轮 , 使 两 根连杆 摆 动 方 向相 反 。水 平 力 小 了一 些 , 但 是
开机 后硬性 冲击 声还 很 重 , 特别 是 向上 的冲 击 力很 大 。原 因是 两根 连杆 长度不 相 等 了 , 质量 差别 大 了 ,
的效 果 。
和两根连杆 形状尺寸相 同、 质量相 等, 运动方 向相
反 。“ 惯性 力平衡 机构 的对 称反 对称 设计 准则 ” 得 到
满足 , 能够设 计 出惯性 力 完全 平衡 机构 。 在机 构 中 , 两个 对应 的构 件运 动速 度相 等 , 运 动 速度方 向必 须 相 反 。这一 点很 关 键 。道 理 很 简 单 , 只有 这样 , 两个 对应 构件 的质 量 和加速 度 的乘积 , 即 惯性 力才 能相 等 , 方 向相 反 , 惯 性力 才 能 完全 抵 消 ,
2 8 ・ 研究与应用 ・
纺织机械
总第 2 5 1期
“ 对 称 反 对 称原 理 ’ ’ 和 机 构 惯 性 力 平 衡
冯 庆 庚
( 烟台经济技术开发 区同步机 电设备研 究所 2 6 4 0 0 6 )
摘
要
介 绍 一种机 构惯 性 力平衡 设计 准 则 , 理 论依 据 是 “ 对称 反 对 称 原理 ” 。显 示 出设 计 成 功 的
2 对 称 反 对 称 原 理
对 称反 对 称 是 客观 存 在 的普 遍 现 象 , 动 物 的肢
图1 对称反 对称机 构的 构件惯性力完全平衡
图1 显 示 的一种 对称 反对 称机 构… 。其 中两 个
滑块是 对称 的 , 两根 连 杆 L是 反对 称 的。两 个 滑 块
体、 器官多数是对称 的, 人们设计的建筑物 、 纺织物 花形 , 往 往也 是 对称 和 反 对 称 的 。对 称 反 对称 已经
机构 惯性 力 完全平衡 原理 图、 电子计 算机 仿 真绘 出的机 构构 件加 速度 曲线 。该技 术 已经 于 2 0 1 2年 通过 中国专利局 发 明 专利 的 实质性 审 查 , 颁发 了发 明专利证 书。
关键 词 对称 机构 惯性 力 平衡
1 前言
判 断一 部机 器 的运 行 品质 好 坏 , 感 受 它 的 噪 声 和振 动 , 是 简单 可 靠 的 方 法 。除 了专 门利 用 振 动 和 噪声工 作 的机器 外 , 一 般 希 望 机 器 的 噪声 和 振 动 越
得到 平衡 。
3 惯性力平衡 机构 的对 称反对称设计准则
笔者 接触 到 大 型 电子 提 花 机 之后 , 了解 到 限制
道 理简单 , 可 是许 多设计 者 的确 没有认 识 到 。 有 一个 企 业 , 高 价从 纺 机 展 上 购买 的 国外 提花 机龙 头 , 一开机, 整个 机 器 在 晃 动 , 连 地 基 都 在 剧烈
构 因配重 多而 变得 复杂 , 恶化 其他 运行 指标 。
在进 行 多次理 论 总结 后 , 才逐 步 认 识 到 机 构设 计 符 合了“ 对 称反 对称 原 理 ” 。笔 者将 其 总结 为 “ 惯 性 力 平 衡机 构 的对称 反对 称设计 准则 ” , 表述为 :
“ 机 构 的对称 平 面两侧 , 对称 或 反对称 构件 的形 状 尺寸 相 同 、 质量 相等 , 运 动方 向相 反” 。
成 为人类 探求 客观 世界 、 创新 设计 的一 种基 本原 理 。 科学 家在 探 讨 宇 宙 和 微 观 物 质 结 构 的前 沿 科 学 领 域, 借用“ 对称 反对称原理” 取 得 了许 多 重 大 发 现 。 应用 “ 对 称反 对称 原 理 ” 研 究 问题 , 会 取 得 事 半功 倍
根长连杆在运行中, 等速同向摆动 , 惯性力叠加到 2
倍 。后来 , 有 几个企 业 对这 种机 型进行 了改进 , 在其
动副 Q、 Y垂直导向。其 中曲柄 r 的值可以改变 , 提
刀梁 可 以 O 或O 4为心 轴 摆 动 , 改变 r 值 可 以形 成 不 同 的开 口大小 和形状 , 适应 不 同织机 、 不 同织造 工
小越 好 。
衡 。笔者 想 到现代 汽 车发动 机 的平衡技 术 , ” 为什 么
小卧车开起来没声音 , 而单缸拖拉机 的振动却让人
难 以忍 受? ” 坚信 总会 找到解 决 问题 的办法 。 经 过几 十 种 设计 方 案 的 比较 , 终 于找 到 了一 种 理 想方 案 , 计 算机仿 真 画 出的动 态 曲线 , 显 示对 应构
所以, 我们 可 以看 到许多 机器 , 只要 能完 成特 定
工作 , 发出的噪声即使很大 , 却一直在运行。在纺织
车间, 织 布机 发 出震 耳 欲聋 的噪 声 , 已经 习惯 , 有 人
认 为“ 高 速往 复运 动是 纺织原 理确 定 的 , 惯性 力产 生
的振 动 和噪声 是必 然 的” 。
