演绎推理课件.ppt
合集下载
演绎推理PPT课件

AB是 C 直角三角形
(结论
(2)函数 y2x5的图象是一条. 直线
归纳
类比
三段论
(特殊到一般) (特殊到特殊)(一般到特殊)
2020年9月28日
8
练一练:请分别说出下列三段论的大小前提和结论?
大前(题1)两条直线平行,同旁内角互补。如果∠A与∠B是两
条平行直线的同旁内角,那么∠A+∠B=180°;
大前题
小前
结论
题
(2)太阳系的大行星都以椭圆形轨道绕太阳运行,
天王星是太阳系的大行星,
三角形是直角三角形,
D
在△ABC中,AD⊥BC,即∠ADB=900 小前提
所以△ABD是直角三角形
结论
同理△ABE是直角三角形
A
M
B
(2)因为直角三角形斜边上的中线等于斜边的一半,大前提
M是Rt△ABD斜边AB的中点,DM是斜边上的中线 小前提
1
所以 DM= 2 AB
结论
同理
EM=
1 2
AB
所以 DM = EM
形式 别到一般的推理。 的推理。
推理。
区
别 推理
结论不一定正确,有待进一
在大前提、小前提 和推理形式都正确
结论 步证明。
的前提下,得到的
结论一定正确。
联系
合情推理的结论需要演绎推理的验证,而演绎 推理的方向和思路一般是通过合情推理获得的。
2020年9月28日
7
推理
合情推理
(或然性推理)
演绎推理 (必然性推理)
大20前20年提9月的28实日 质是使推理得以进行下去的依据。大前提往往省略11
例2 利用三段论证明:函数 f (x)=-x2+2 x在(-∞,1)是 增函数.
课件5:2.1.2 演绎推理

∵直角三角形斜边上的中线等于斜边的一半,大前提 M 是直角△ABD 斜边 AB 上的中点,DM 为中线,小前提 ∴DM=12AB. ……………………………………结论 同理 EM=12AB.
∵和同一条线段相等的两条线段相等,……大前提 DM=12AB,EM=12AB,……………………小前提 ∴MD=ME. ……………………………………结论
解:(1)三角函数是周期函数,………………大前提 y=sin x(x∈R)是三角函数,…………………小前提 y=sin x(x∈R)是周期函数.…………………结论 (2)两个角是对顶角,则这两个角相等,……大前提 ∠1 和∠2 是对顶角,………………………小前提 ∠1 和∠2 相等.………………………………结论
(3)所有的循环小数都是有理数,……………大前提 0.332·是循环小数,…………………………小前提 0.332·是有理数.………………………………结论
所以,b a
a+m a+m
<a a
b+m a+m
,即ba<ba+ +mm.……结论
随堂演练 1.“四边形 ABCD 是矩形,所以四边形 ABCD 的对角线 相等”,补充该推理的大前提是 ( ) A.正方形的对角线相等 B.矩形的对角线相等 C.等腰梯形的对角线相等 D.矩形的对边平行且相等
【解析】得出“四边形 ABCD 的对角线相等”的大前提 是“矩形的对角线相等”. 【答案】B
③函数 f(x)=x+1x在(1,+∞)上为增函数.
5.将下列推理写成“三段论”的形式. (1)向量是既有大小又有方向的量,故零向量也有大小 和方向; (2)矩形的对角线相等,正方形是矩形,所以正方形的 对角线相等; (3)0.332·是有理数.
解:(1)向量是既有大小又有方向的量,……大前提 零向量是向量,………………………………小前提 零向量也有大小和方向.………………………结论 (2)每一个矩形的对角线相等,………………大前提 正方形是矩形,………………………………小前提 正方形的对角线相等.…………………………结论
6.2 简单判断的演绎推理方法 课件(44张PPT)

三段论推理
1.三段论推理的含义
三段论是演绎推理的一种重要形式。它是以两个已知的性质判断 为前提,借助一个共同的项推出一个新的性质判断的推理。
2.三段论推理的结构
中项 所有 M 都是 P 大前提 所有 S 都是 M 小前提
所以,所有 S 都是 P 结论
小项
大项
P M S
结构式
三段论推理
【探究与分享】
6.2 简单判断的演绎推理方法
第六课 掌握演绎推理方法
第二单元 遵循逻辑思维规则
性质判断换质推理
示例评析
◆所有金属都是导电的,
所以,所有金属都不是不导电的。
◆唯心主义者不是马克思主义者,所以,唯心主义者是非马克思主义者。
◆有些学生是党员,
所以,有些学生不是非党员。
◆有些疾病不是传染的,
所以,有些疾病是不传染的。
指的是性质判断形式的肯定或否定。
性质判断换质推理
肯定判断形式→否定判断形式 否定判断形式→肯定判断形式
所有 书信 是 有格式的 所有 书信 不是 没有格式的
量项和主项
不变
联项
换质
新谓项是与原谓
项相矛盾的概念
性质判断换质推理
(3)规则
从所给真实前提必然地推出真实结论必须遵循的规则: ①推理时不改变前提判断的主项和量项。 ②改变前提判断的质,即把肯定判断变为否定判断,把 否定判断变为肯定判断。 ③找出前提性质判断中与谓项相矛盾的概念,用它作为 结论性质判断的谓项。
性质判断换位推理
第一步:不改变 联项。主项与谓 项的位置互换。
量项 主项 联项 谓项
第二步:前提中 不周延的项换位 后不能周延。
(新) 量项
新主项
《演绎推理》PPT课件

错误:中项两次不周延
精选课件ppt
22
例如:凡贪污罪都是故意犯罪, 某人的行为是故意犯罪,
所以,某人的行为是贪污罪。
辩证法是马克思主义的精髓 黑格尔的方法是辩证法 所以,黑格尔的方法是马克思主义的精髓
精选课件ppt
23
2、在前提中不周延的项,在结论中也不得周延
错误:大项不当周延小项不当周延 例: a. 海鸥是会飞的
直言判断推理 关系推理 模态推理
直接推理 三段论
复合判断推理
完全归纳推理 不完全归纳推理
联言推理 选言推理 假言推理 假言选言推理
简单枚举归纳推理 科学归纳推理
精选课件ppt
8
第二节 直言判断直接推理
一、什么是直言判断直接推理 二、直言判断对当关系推理 三、直言判断变形直接推理
精选课件ppt
9
一、什么是直言判断直接推理
出一个新判断的思维形态。 例:真金是不怕火炼的,
所以,怕火炼的不是真金。
凡绿色植物都是含有叶绿素的, 菠菜是绿色植物, 所以,菠菜是含有叶绿素的。
精选课件ppt
4
二、推理的组成
1、前提:已知的作为推理出发点的判断。 2、结论:有前提推出的新判断。 3、推理形式:前提与结论之间的联结方式。
精选课件ppt
5
三、结论真实的推理和合乎逻辑的推理
结论真实的推理具备的条件: 1、前提真实 2、推理形式有效 例:凡有用的都是真理,
所以,凡真理都是有用的。
运动员需要锻炼身体, 我不是运动员, 所以,我不用锻炼身体
精选课件ppt
6
四、推理作用
精选课件ppt
7
五、推理的种类
推理
演绎推理
归纳推理 类比推理
精选课件ppt
22
例如:凡贪污罪都是故意犯罪, 某人的行为是故意犯罪,
所以,某人的行为是贪污罪。
辩证法是马克思主义的精髓 黑格尔的方法是辩证法 所以,黑格尔的方法是马克思主义的精髓
精选课件ppt
23
2、在前提中不周延的项,在结论中也不得周延
错误:大项不当周延小项不当周延 例: a. 海鸥是会飞的
直言判断推理 关系推理 模态推理
直接推理 三段论
复合判断推理
完全归纳推理 不完全归纳推理
联言推理 选言推理 假言推理 假言选言推理
简单枚举归纳推理 科学归纳推理
精选课件ppt
8
第二节 直言判断直接推理
一、什么是直言判断直接推理 二、直言判断对当关系推理 三、直言判断变形直接推理
精选课件ppt
9
一、什么是直言判断直接推理
出一个新判断的思维形态。 例:真金是不怕火炼的,
所以,怕火炼的不是真金。
凡绿色植物都是含有叶绿素的, 菠菜是绿色植物, 所以,菠菜是含有叶绿素的。
精选课件ppt
4
二、推理的组成
1、前提:已知的作为推理出发点的判断。 2、结论:有前提推出的新判断。 3、推理形式:前提与结论之间的联结方式。
精选课件ppt
5
三、结论真实的推理和合乎逻辑的推理
结论真实的推理具备的条件: 1、前提真实 2、推理形式有效 例:凡有用的都是真理,
所以,凡真理都是有用的。
运动员需要锻炼身体, 我不是运动员, 所以,我不用锻炼身体
精选课件ppt
6
四、推理作用
精选课件ppt
7
五、推理的种类
推理
演绎推理
归纳推理 类比推理
演绎推理 课件

解 在数列{an}中,如果当n≥2时,an-an-1为常数,则{an}为等差数列, 大前提
当通项公式为an=2n+3时,若n≥2, 则an-an-1=2n+3-[2(n-1)+3]=2(常数), 通项公式为an=2n+3的数列{an}为等差数列.
小前提 结论
类型二 演绎推理的应用
命题角度1 证明几何问题 例2 如图,D,E,F分别是BC,CA,AB上的点,∠BFD=∠A, DE∥BA,求证:ED=AF,写出三段论形式的演绎推理.
解 平行四边形的对角线互相平分, 菱形是平行四边形, 菱形的对角线互相平分.
大前提 小前提 结论
②等腰三角形的两底角相等,∠A,∠B是等腰三角形的两底角,则∠A= ∠B;
解 等腰三角形的两底角相等, ∠A,∠B是等腰三角形的两底角, ∠A=∠B.
大前提 小前提 结论
③通项公式为an=2n+3的数列{an}为等差数求f(x)的单调递增区间.
梳理 三段论的基本模式
大前提 小前提
结论
一般模式 _已__知__的__一__般__原__理___ _所__研__究__的__特__殊__情__况___ 根据一般原理,对特殊情况做出的判断
常用格式 M是P S是M S是P
类型一 演绎推理与三段论
例1 将下列演绎推理写成三段论的形式. ①平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线 互相平分;
演绎推理
知识点一 演绎推理
思考 分析下面几个推理,找出它们的共同点. (1)所有的金属都能导电,铀是金属,所以铀能够导电; (2)一切奇数都不能被2整除,(2100+1)是奇数,所以(2100+1)不能被2整除. 答案 问题中的推理都是从一般性的原理出发,推出某个特殊情况下的 结论,我们把这种推理叫演绎推理.
演绎推理 课件

演绎推理
知识点一 演绎推理及其一般模式——“三段论” 1.演绎推理
含义 从一般性的原理出发,推出_某个特殊情况下的结论的推理
特点 2.三段论
大前提 小前提
结论
由 一般到特殊 的推理
一般模式
已知的一般原理 所研究的特殊情况
根据一般原理,对特殊情况做出的判断
常用格式 M是P S是M S是P
思考 (1)演绎推理的应用
例3 如图所示,三棱锥 A-BCD的三条侧棱AB, AC,
AD两两互相垂直,O为点A在底面BCD上的射影. (1)求证: O为△BCD的垂心;
证明 ∵AB⊥AD,AC⊥AD,AB∩AC=A,
∴AD⊥平面ABC,又BC⊂平面ABC.
∴AD⊥BC,又∵AO⊥平面BCD,AO⊥BC,
_ 提下,得到的结论一定正确
别
具有猜测和发现结论,探索 按照严格的逻辑法则推理,利
作用 和提供思路的作用,利于创 于培养和提高逻辑证明的能力
新意识的培养
联系
合情推理与演绎推理是相辅相成的,数学结论、证明思路等 的发现主要靠合情推理;数学结论、猜想的正确性必须通过 演绎推理来证明
题型一 用三段论的形式表示演绎推理
∵AD∩AO=A,
∴BC⊥平面AOD,∴BC⊥DO,同理可证 CD⊥BO,
(2)类比平面几何的勾股定理, 猜想此三棱锥侧面与底面间的一个关系, 并给出证明.
证明如下: 连接DO并延长交BC于E,连接AE, 由(1)知AD⊥平面ABC,AE⊂平面ABC, ∴AD⊥AE,又AO⊥ED, ∴AE2=EO·ED,
∵a, b, c∈R+,
利用三段论推理时, 正确使用大(小)前提, 尤其注意数学中有关公式、定 理、性质、法则的使用情形.
知识点一 演绎推理及其一般模式——“三段论” 1.演绎推理
含义 从一般性的原理出发,推出_某个特殊情况下的结论的推理
特点 2.三段论
大前提 小前提
结论
由 一般到特殊 的推理
一般模式
已知的一般原理 所研究的特殊情况
根据一般原理,对特殊情况做出的判断
常用格式 M是P S是M S是P
思考 (1)演绎推理的应用
例3 如图所示,三棱锥 A-BCD的三条侧棱AB, AC,
AD两两互相垂直,O为点A在底面BCD上的射影. (1)求证: O为△BCD的垂心;
证明 ∵AB⊥AD,AC⊥AD,AB∩AC=A,
∴AD⊥平面ABC,又BC⊂平面ABC.
∴AD⊥BC,又∵AO⊥平面BCD,AO⊥BC,
_ 提下,得到的结论一定正确
别
具有猜测和发现结论,探索 按照严格的逻辑法则推理,利
作用 和提供思路的作用,利于创 于培养和提高逻辑证明的能力
新意识的培养
联系
合情推理与演绎推理是相辅相成的,数学结论、证明思路等 的发现主要靠合情推理;数学结论、猜想的正确性必须通过 演绎推理来证明
题型一 用三段论的形式表示演绎推理
∵AD∩AO=A,
∴BC⊥平面AOD,∴BC⊥DO,同理可证 CD⊥BO,
(2)类比平面几何的勾股定理, 猜想此三棱锥侧面与底面间的一个关系, 并给出证明.
证明如下: 连接DO并延长交BC于E,连接AE, 由(1)知AD⊥平面ABC,AE⊂平面ABC, ∴AD⊥AE,又AO⊥ED, ∴AE2=EO·ED,
∵a, b, c∈R+,
利用三段论推理时, 正确使用大(小)前提, 尤其注意数学中有关公式、定 理、性质、法则的使用情形.
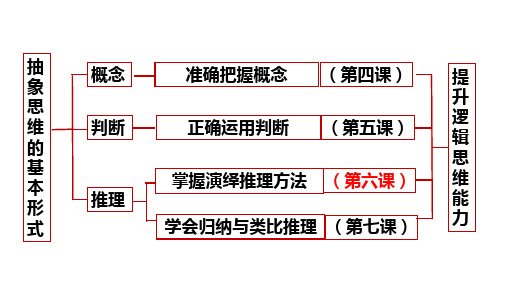
6.1 推理与演绎推理概述 课件(共27张PPT)高中政治统编版选择性必修3 逻辑与思维
甲说乙说谎,乙说丙说谎,丙说甲和乙都说谎。以下正确的说法是( ) A.甲和乙诚实,丙是说谎者 B.甲和丙说谎,乙是诚实者 C.乙和丙说谎,甲是诚实者 D.乙和丙诚实,甲是说谎者
解析: ①根据题干三个条件,假设甲诚实,那么乙就是说谎者;乙是说 谎者,则丙诚实;若丙诚实,则甲和乙都是说谎者,这个推演结果与我 们的初始假设“甲诚实”不一致(矛盾),于是可定论:甲不诚实。②从 定论“甲不诚实”,可推知乙诚实;从乙诚实,推知丙说谎;从丙说谎, 推出甲和乙不都说谎(乙诚实),推演结果成立,结论是:甲和丙说谎, 乙诚实。故选B。
作案的 不是我
甲
乙
丙
丁
经查证,四个人的口供中只有一个是假的。➢ 谁是作案人?你的结论是如何得出的。
推理过程: 乙:丁是案犯
丁:作案的不是我
两判断有矛盾,根据矛盾律,不可能同真,必有一假
四个人的口供中只有一个是假的。
甲:案犯是丙 丙:如果我作案,那么丁是主犯
根据矛盾律,乙、丁必有一假
甲、丙为真
丙、丁为作案人 (丁说了假话)
形式逻辑的研究对象是推理结构,不研究每个推理所反映的认识对象的 具体内容。
①告诉人们正确的思维应该运用怎样的推理结构,以及运用推理结 构时应该遵循哪些规则; ②帮助人们识别什么样的推理结构是正确的,什么样的推理结构是 不正确的。
正确理解:逻辑学不研究每个推理所反映的认识对象的具体内容。 逻辑学本身只能告诉我们前提和结论之间的逻辑规则,而不具体解决前提真实与否 的问题。前提真实与否只有靠各门具体科学,靠实践来解决。
一、推理的含义与种类
1、判断形成的两条途径
一是通过实践,直接对对象进行观察或调查,然后作出判断; 二是借助已有的判断,合乎逻辑地推出一个新的判断。(推理)
人教a版数学【选修2-2】2.1.2《演绎推理》ppt课件

重点:演绎推理的含义及演绎推理规则. 难点:演绎推理的应用.
演绎推理 思维导航 日常生活中我们经常接触这样的推理形式:“所有金属都导 电,因为铁是金属,所以铁导电”,它是合情推理吗?这种 推理形式正确吗?
新知导学 1.演绎推理 从________________出发,推出__________情况下的结论, 一般性的原理 某个特殊 我们把这种推理称为演绎推理,简言之,演绎推理是由 _____________的推理. 一般到特殊
6.判断下列推理是否正确?为什么? “因为过不共线的三点有且仅有一个平面(大前提),而A、B 、C为空间三点(小前提),所以过A、B、C三点只能确定一个 平面(结论).” [解析] 不正确,因为大前提中的“三点”不共线,而小前 提中的“三点”的基本形式——三段论
3.三段论 (1)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的__________; 一般原理 ②小前提——所研究的__________; 特殊情况 ③结论——根据一般原理,对特殊情况做出的________. 判断 其一般推理形式为 大前提:M是P. 小前提:S是M. 结 论:__________.
成才之路 · 数学
人教A版 · 选修2-2
路漫漫其修远兮 吾将上下而求索
第二章
推理与证明
第二章 2.1 合情推理与演绎推理
2.1.2 演绎推理
1
自主预习学案
2
典例探究学案
3
巩固提高学案
4
备 选 练 习
自主预习学案
理解演绎推理的概念,掌握演绎推理的形式,并能用它们进 行一些简单的推理,了解合情推理与演绎推理的联系与区别 .
牛刀小试 1 . (2014· 微山一中高二期中 )关于下面推理结论的错误: “因为对数函数 y=logax 是增函数(大前提),又 y=log1 x 是对
