报告高数函数图形的描绘.ppt
合集下载
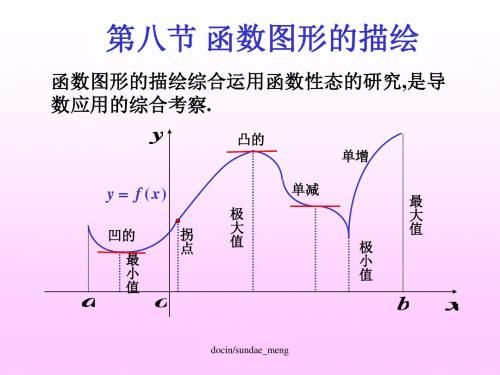
——函数图形的描绘PPT课件

lim f (x) ;
xa
(iii)
lim f (x) ;
xa
(iv)
. lim f (x)
xa
第11页/共27页
以上四种情形可参考下列各图
a
a (图 (i))
(图 (ii)) a
a (图 (iii))
(图 (iv)) 第12页/共27页
如果下列条件之一成立,则称直线 y a 为 f 之 水平渐近线:
(i) lim f (x) a ; a
(ii) lim f (x) a . x
以上二种情形可参考下列各图:
a
(图 2.3.2(i))
a
(图 2.3.2(ii))
第13页/共27页
如果下列条件之一成立,则称直线
y ax b ,( a 0 )为 f 之斜渐近线:
(i)
lim f (x) (ax b) 0 ;
曲线 在(,0]为凸的; 当x 0时, y 0, 曲线 在[0,)为凹的; 注意到, 点(0,0)是曲线由凸变凹的分界点.
第4页/共27页
➢曲 线 的 拐 点 及 其 求 法
1、定义 连续曲线上凹凸的分界点称为曲线的拐点. 注意:拐点处的切线必在拐点处穿过曲线. 2、拐点的求法
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
点(0 , 0)为拐点.
其相关结论见表:
x (, 1) -1 (-1,0) 0 (0, 1) 1 (1, )
f (x) +
0
-
-
-0Βιβλιοθήκη +f (x) -
-
-
0
+
+
+
f (x)
高数函数图形的描绘ppt课件

的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
3/30/2020
6
例3. 描绘
的图形.
解: 1) 定义域为
无对称性及周期性.
2) y x2 2x, y 2x 2,
y
令 y 0,
令 y 0,
1 O 1 2 3 x
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
,
渐近线
y 1
.
提示:
y 2 ex2 (1 2 x2 )
y
1
1
( 1 ,1 e 2 )
2
O
(
1
,1
1
e2 )
2
x
3/30/2020
16
作业
P76 14 (2); P169 2 ; 5
3/30/2020
17
第七节
备用题 求笛卡儿叶形线 x3 y3 3axy 的渐近线 .
解: 令 y = t x , 代入原方程得曲线的参数方程 :
2π
令 y 0 得 x 0; 令 y 0 得 x 1
3) 判别曲线形态
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1 2π
1 2πe
(极大)
(拐点)
3/30/2020
12
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1 2π
1 2πe
(极大)
(拐点)
4) 求渐近线
lim y 0
第六节 函数图形的描绘
一、 曲线的渐近线 二、 函数图形的描绘
【中学课件】函数图形的描绘-PPT文档资料
x( 2 ,0 ) 3 , 2 ) 2 ( , 3 ) 3 (
f (x)
0
不存在
(0 , )
f (x)
0 0
拐点
( 3, 26 ) 9
f ( x)
极值点
docin/sundae_meng
3
间 断 点
补充点 : ( 1 3 , 0 ), ( 1 3 , 0 );
y . 2
2、图形描绘的步骤
利用函数特性描绘函数图形.
第一步
y f ( x ) 确 定 函 数 的 定 义 域 , 利 用 函 数 奇 偶 性 、 周 期 性 缩 小 范 围 ;
确 定 特 殊 点 : 曲 线 与 x 轴 的 交 点 , 即 : f ( x ) = 0 ; ' " f ( x ) 0 f( x ) 0 使 和 及 导 数 不 存 在 的 点 .
第二步
docin/sundae_meng
用 特 殊 点 将 函 数 的 定 义 域 划 分 成 几 个 部 f'( x )和 分 区 间 , 列 成 表 格 .确 定 在 这 些 部 分 区 间 内 f" ( x ) 的 符 号 , 并 由 此 确 定 函 数 的 增 减 性 、 极 值 和 函 数 的 凹 凸 性 和 拐 点 。
4 ( x 2 ) f ( x ) 3 , 4 ( x 1 ) x , lim f ( x ) lim [ 2 2 ] x 0 x 0 x 8 (x 3 ) f (x ) . 得铅直渐近线 x0 . 4 x
列表确定函数升降区间,凹凸区间及极值点和拐点:
docin/sundae_meng
3、作图举例
高中数学函数的图像ppt课件

34
真题透析 例 (2010 年高考湖南卷)函数 y=ax2+bx 与 y = logb x(ab≠0,|a|≠|b|)在同一直角坐标系中的图
a
像可能是( )
35
【解析】 从对数的底数入手进行讨论,再 结合各个选项的图像从抛物线对称轴的取值 范围进行判断,故选D. 【答案】 D 【名师点评】 (1)本题易出现以下错误:① 忽视 y= logb x 中底数的绝对值,误认为 a,b
(2)图像的左右平移,只体现出x的变化,与x 的系数无关;图像的上下平移,只与y的变化 有关.
19
识图 对于给定函数的图像,可从图像上下左右分布范 围,变化趋势,特殊点的坐标等方面进行判断, 必要时可借助解方程、解(证)不等式等手段进行 判断,未必非要写出函数的解析式进行判断.
20
例2
(2010年高考山东卷)函数y=2x-x2的图像
过点 P 且与 AB 垂直的截面面积记为 y,则 y=
12f(x)的大致图像是(
)
38
解析:选A.先从起始点排除B,D,再用验证 法,当点P为OA的中点时,截面面积大于大圆 面积的一半,即可判定A正确.
39
x+1,x∈[-1,0 2.已知 f(x)=x2+1,x∈[0,1] ,则下 列函数的图像错误的是( )
11
5.已知下列曲线: 以下编号为①②③④的四个方程 ① x- y=0;②|x|-|y|=0;③x-|y|=0; ④|x|-y=0. 请按曲线 A、B、C、D 的顺序,依次写出与 之对应的方程的编号________.
答案:④②①③
12
考点探究•挑战高考
考点突破
作图 1.熟悉基本初等函数的图像. 2.会通过函数的性质确定图像的形状:如奇偶 性→对称性;函数值的正负→x轴上方下方;渐 近线→变化趋势;过哪些特殊点、定点;极值、 最值等.
真题透析 例 (2010 年高考湖南卷)函数 y=ax2+bx 与 y = logb x(ab≠0,|a|≠|b|)在同一直角坐标系中的图
a
像可能是( )
35
【解析】 从对数的底数入手进行讨论,再 结合各个选项的图像从抛物线对称轴的取值 范围进行判断,故选D. 【答案】 D 【名师点评】 (1)本题易出现以下错误:① 忽视 y= logb x 中底数的绝对值,误认为 a,b
(2)图像的左右平移,只体现出x的变化,与x 的系数无关;图像的上下平移,只与y的变化 有关.
19
识图 对于给定函数的图像,可从图像上下左右分布范 围,变化趋势,特殊点的坐标等方面进行判断, 必要时可借助解方程、解(证)不等式等手段进行 判断,未必非要写出函数的解析式进行判断.
20
例2
(2010年高考山东卷)函数y=2x-x2的图像
过点 P 且与 AB 垂直的截面面积记为 y,则 y=
12f(x)的大致图像是(
)
38
解析:选A.先从起始点排除B,D,再用验证 法,当点P为OA的中点时,截面面积大于大圆 面积的一半,即可判定A正确.
39
x+1,x∈[-1,0 2.已知 f(x)=x2+1,x∈[0,1] ,则下 列函数的图像错误的是( )
11
5.已知下列曲线: 以下编号为①②③④的四个方程 ① x- y=0;②|x|-|y|=0;③x-|y|=0; ④|x|-y=0. 请按曲线 A、B、C、D 的顺序,依次写出与 之对应的方程的编号________.
答案:④②①③
12
考点探究•挑战高考
考点突破
作图 1.熟悉基本初等函数的图像. 2.会通过函数的性质确定图像的形状:如奇偶 性→对称性;函数值的正负→x轴上方下方;渐 近线→变化趋势;过哪些特殊点、定点;极值、 最值等.
函数图形的描绘

2. 斜渐近线 若
(或 x )
( k x b) ( k x b)
斜渐近线 y k x b .
f ( x) b lim x[ k ]0 x x x f ( x) b lim [ k ]0 x x x
f ( x) b 即 k lim [ ] x x x
1 令 f ( x ) = 0, 得可疑点: x 2
lim f ( x ) lim e
x x x2
0
得水平渐近线 y 0 ,
曲线 y f ( x ) 不存在其它渐近线.
列表确定函数单调区间,凹凸区间,极值点和拐点:
x
f ( x ) f ( x )
1 1 1 (, ) ( ,0) 2 2 2
第六节 函数图形的描绘
第六节 函数图形的描绘
一、曲线的渐近线 二、函数图形的描绘
三、内容小结
返回
一、 曲线的渐近线 定义 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为 曲线C 的渐近线 . 或为“纵坐标差”
y
C M
y f ( x)
解:
定义域: (,0) (0,)
f ( x ) 4( x 2) , 3 x f ( x ) 8( x 3) . 4 x
令 f ( x ) 0, 得驻点 x 2, 令 f ( x ) 0, 得点 x 3.
4( x 1) lim f ( x ) lim [ 2] 2 得水平渐近线 y 2 , 2 x x x
y kxb
L
PN
例如, 双曲线 有渐近线
o
x y 0 a b
chap3-6函数图形的描绘 共22页

机动 目录 上页 下页 返回 结束
第三步 确 定 在 这 些 部 分 区 间 内 f'(x)和 f"(x)的 符 号 , 并 由 此 确 定 函 数 的 增 减 性 与 极 值 及 曲 线 的 凹 凸 与 拐 点 ( 可 列 表 进 行 讨 论 ) ;
第四步 确定函数图形的水平、铅直渐近线、斜渐 近线以及其他变化趋势;
那么yaxb就是y f(x)的一条斜渐 . 近
斜渐近线求法:
limf(x) a, li[m f(x)a]x b.
x x
x
那y么 a xb就是y 曲 f(x)线 的一条.斜
机动 目录 上页 下页 返回 结束
注意: 如果
(1) lim f (x) 不存在; x x
(2 )lif m (x )a存 ,但 在 li[m f(x ) a]不 x ,存
0
0
f(x) f (x)
极大值
32
27
拐点
( 1 , 16 ) 3 27
极小值
0
y
B(0,1)
C (3,5) 28
A(1,0)
1
1 o 1
3
3
1
x
机动 目录 上页 下页 返回 结束
yx3x2x1
机动 目录 上页 下页 返回 结束
四、小结
函数图形的描绘综合运用函数性态的研究,是导 数应用的综合考察.
x x
x
可以断 y定 f(x)不存在斜.渐近线
例1 求f(x)2(x2)x (3)的渐. 近线 x1
解 D :(,1 ) (1 ,) .
机动 目录 上页 下页 返回 结束
limf(x), x1
第三步 确 定 在 这 些 部 分 区 间 内 f'(x)和 f"(x)的 符 号 , 并 由 此 确 定 函 数 的 增 减 性 与 极 值 及 曲 线 的 凹 凸 与 拐 点 ( 可 列 表 进 行 讨 论 ) ;
第四步 确定函数图形的水平、铅直渐近线、斜渐 近线以及其他变化趋势;
那么yaxb就是y f(x)的一条斜渐 . 近
斜渐近线求法:
limf(x) a, li[m f(x)a]x b.
x x
x
那y么 a xb就是y 曲 f(x)线 的一条.斜
机动 目录 上页 下页 返回 结束
注意: 如果
(1) lim f (x) 不存在; x x
(2 )lif m (x )a存 ,但 在 li[m f(x ) a]不 x ,存
0
0
f(x) f (x)
极大值
32
27
拐点
( 1 , 16 ) 3 27
极小值
0
y
B(0,1)
C (3,5) 28
A(1,0)
1
1 o 1
3
3
1
x
机动 目录 上页 下页 返回 结束
yx3x2x1
机动 目录 上页 下页 返回 结束
四、小结
函数图形的描绘综合运用函数性态的研究,是导 数应用的综合考察.
x x
x
可以断 y定 f(x)不存在斜.渐近线
例1 求f(x)2(x2)x (3)的渐. 近线 x1
解 D :(,1 ) (1 ,) .
机动 目录 上页 下页 返回 结束
limf(x), x1
高等数学课件D3_6函数图形的描绘

例
描绘
y
1 3
x3
x2
2
的图形.
解: 1) 定义域为(, ),无对称性及周期性.
2) y x2 2x, y 2x 2,
y
令 y 0, 得 x 0, 2
令 y 0, 得 x 1
1 O 1 2 3 x
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
y 0
0
x 0 (0, 1) 1 (1, )y 0 Nhomakorabeay
0
y
1 2π
1 2πe
(极大)
(拐点)
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1 2π
1 2πe
(极大)
(拐点)
4) 求渐近线
lim y 0
x
y 0 为水平渐近线
5) 作图
y
1 2π
A
y0 O
y
1
x2
e2
2π
B
1
x
思考与练习
y
y
x 1 3
4)
y
2 3
2
2
(极大)
0
4 3
(拐点)
2 3
(极小)
例
描绘函数 y
1
e
x2 2
的图形.
2π
解: 1) 定义域为 (, ), 图形对称于 y 轴.
2) 求关键点
y
1 2π
x
e
x2 2
,
y
1
e
x2 2
(1
x
2
)
2π
令 y 0得 x 0; 令 y 0 得 x 1
【中学课件】函数图形的描绘

f ( x)
0 不存在
f (x)
0
f (x)
拐点
极值点
3 (3, 2h6tt)p:///sundae_meng 9
间 断 点
补充点: (1 3,0), (1 3,0);
A (1,2), 作图
B (1,6), C (2,1). y
得特殊点 x 1 . 3
补充点: A (1,0),
B (0,1), C (3 , 5). 28
列表确定函数升降区间, 凹凸区间及极值点与拐点:
/sundae_meng
x (, 1) 1 ( 1 , 1) 1
3
3 33
3
f (x)
0
第五步 描出与方程 f '( x) 0 和 f "( x) 0 的根对 应的曲线上的点,有时还需要补充一些点,再综 合前四步讨论的结果画出函数的图形.
/sundae_meng
3、作图举例
例1
作函数
f
(
x)
4(
x x2
1)
2
的图形.
解 D : x 0, 非奇非偶函数,且无对称性.
有铅直渐近线两条: x 2, x 3.
/sundae_meng
水平渐近线 (平行于 x 轴的渐近线)
如果 lim f ( x) b 或 lim f ( x) b (b 为常数)
x
x
那么 y b 就是 y f ( x) 的一条水平渐近线.
1
x
例3 作函数 f ( x) x3 x2 x 1 的图形.
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)(x 1), f ( x) 2(3x 1).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
f
(x)
x]
lim
x
2x2 3x x2 2x 3
y x 2为曲线的斜渐近线 .
演示课件
二、函数图形的描绘
步骤 :
1. 确定函数 期性 ;
的定义域 , 并考察其对称性及周
2. 求
并求出 及
为 0 和不存在
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
1)
,
y
(
x
2 1)3
演示课件
又因
lim y 1 , 即 k 1
x x 4
4
b lim ( y 1 x) lim [(x 3)2 1 x] x 4 x 4(x 1) 4
lim 5x 9 5 x 4(x 1) 4
y 1 x 5 为斜渐近线 44
5) 求特殊点 x 0 2 y 9 1 44
2 1
O12 3 5 x
y
1 4
x
5 4
x 1
演示课件
例5. 描绘函数
的图形.
解: 1) 定义域为
图形对称于 y 轴.
2) 求关键点
y
1 2π
x
e
x2 2
,
y
1
e
x2 2
(1
x
2
)
2π
令 y 0 得 x 0; 令 y 0 得 x 1
3) 判别曲线形态
x 0 (0, 1) 1 (1, )
y (x 3)2 4(x 1)
y
(
x 4(
3)(x x 1)2
1)
y
(
x
2 1)3
演示课件
6)绘图
x (, 1) 1 (1,1)
y
2
(极大)
铅直渐近线 x 1
斜渐近线
y1x5 44
特殊点
x0 y 9
2 1
44
1 (1,3) 3 (3, )
无
0
定 义
(极小)
y
y (x 3)2
4(x 1)
lim y
x
(x)
lim 3a t 2
t 1 1 t 3
3at 1 t3
lim
t 1
3 at(1t) (1t)(1t t
2
)
a
所以笛卡儿叶形线有斜渐近线 y x a
笛卡儿 叶形线
演示课件
叶形线
演示课件
第七节
备用题 求笛卡儿叶形线 x3 y3 3axy 的渐近线 .
解: 令 y = t x , 代入原方程得曲线的参数方程 :
x
3at 1 t3
,
3at2 y 1t3 ,
当x 时t 1, 因
t 1
lim y lim 3a t 2 3a t 1 x x t1 1 t 3 1 t 3
斜渐近线
2. 函数图形的描绘
按作图步骤进行
演示课件
思考与练习
D 1.
曲线
y
1 1
ex2 ex2
(
)
(A) 没有渐近线;
(B) 仅有水平渐近线;
(C) 仅有铅直渐近线; (D) 既有水平渐近线又有铅直渐近线.
提示:
lim
x
1 1
e e
x x
2 2
1;
lim 1 x01
e e
x x
2 2
演示课件
演示课件
2 3
(极小)
例4. 描绘方程
的图形.
解: 1) y (x 3)2 , 定义域为 4(x 1)
2) 求关键点. 原方程两边对 x 求导得
2(x 3) 4 y 4 y 4xy 0
①
y x 3 2y 2(x 1)
①两边对 x 求导得 2 4 y 8y 4xy 0
y 1 4 y 2(x 1)
x x
x
b lim [ f (x) k x]
x (或 x )
演示课件
例2. 求曲线
的渐近线.
y
解:
y
x3
,
(x 3)(x 1)
lim y ,
x 3
(或 x 1)
3 O1 x
y x2
所以有铅直渐近线 x 3 及 x 1
又因
ቤተ መጻሕፍቲ ባይዱ
k
lim
x
f (x) x
lim
x
x2
x2 2x
3
b
lim [
2. 曲线 y 1 ex2 的凹区间是
( 1 , 1 )
22
,
凸区间是
( ,
1 )
2
及
(
1 , )
2
,
拐点为
(
1
1
,1e 2 )
2
,
渐近线
y 1
.
提示:
y 2 ex2 (1 2 x2 )
y
1
1
( 1 ,1 e 2 )
2
O
(
1
,1
1
e2 )
2
x
演示课件
作业
P76 14 (2); P169 2 ; 5
令 y 0 得 x 1, 3 ;
演示课件
3) 判别曲线形态
x (, 1) 1
y
0
y
y
2
(1,1)
1 (1,3) 3
无
0
定
义
0
(3, )
(极大)
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
y (x 3)2 , 4(x 1)
y
(
x 4(
3)(x x 1)2
第六节 函数图形的描绘
一、 曲线的渐近线 二、 函数图形的描绘
演示课件
一、 曲线的渐近线
定义 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为
曲线C 的渐近线 .
y
y f (x)
或为“纵坐标差” C M
y kxb
例如, 双曲线
L PN
演示课件
2. 斜渐近线 ( P76 题14)
若
(kx b)
(或 x )
(kx b)
lim x [ f (x) k b ] 0
x
x
x
斜渐近线 y k x b. k lim [ f (x) b ]
x x x k lim f (x)
x x
(或 x )
lim [ f (x) k b ] 0
演示课件
例3. 描绘
的图形.
解: 1) 定义域为
无对称性及周期性.
2) y x2 2x, y 2x 2,
y
令 y 0,
令 y 0,
1 O 1 2 3 x
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
y
0
0
y y
x 1 3
4)
y2
3
2
0
2
4 3
(极大)
(拐点)
y 0
y
y
1 2π
0
1
2πe
(极大)
(拐点)
演示课件
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1 2π
1 2πe
(极大)
(拐点)
4) 求渐近线
lim y 0
x
y 0 为水平渐近线
5) 作图
y
1 2π
A
y0 O
y
1
x2
e2
2π
B
1
x
演示课件
内容小结
1. 曲线渐近线的求法
水平渐近线 ; 垂直渐近线;
有渐近线
x y0 ab
O
x
y
但抛物线
无渐近线 .
Ox
演示课件
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或 x )
若
则曲线
有铅直渐近线 x x0 .
(或 x x0 )
y
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2 x x 1
2
x
O1
y 2 为水平渐近线;
lim( 1 2) , x 1为铅直渐近线. x1 x 1
f
(x)
x]
lim
x
2x2 3x x2 2x 3
y x 2为曲线的斜渐近线 .
演示课件
二、函数图形的描绘
步骤 :
1. 确定函数 期性 ;
的定义域 , 并考察其对称性及周
2. 求
并求出 及
为 0 和不存在
的点 ;
3. 列表判别增减及凹凸区间 , 求出极值和拐点 ;
4. 求渐近线 ;
5. 确定某些特殊点 , 描绘函数图形 .
1)
,
y
(
x
2 1)3
演示课件
又因
lim y 1 , 即 k 1
x x 4
4
b lim ( y 1 x) lim [(x 3)2 1 x] x 4 x 4(x 1) 4
lim 5x 9 5 x 4(x 1) 4
y 1 x 5 为斜渐近线 44
5) 求特殊点 x 0 2 y 9 1 44
2 1
O12 3 5 x
y
1 4
x
5 4
x 1
演示课件
例5. 描绘函数
的图形.
解: 1) 定义域为
图形对称于 y 轴.
2) 求关键点
y
1 2π
x
e
x2 2
,
y
1
e
x2 2
(1
x
2
)
2π
令 y 0 得 x 0; 令 y 0 得 x 1
3) 判别曲线形态
x 0 (0, 1) 1 (1, )
y (x 3)2 4(x 1)
y
(
x 4(
3)(x x 1)2
1)
y
(
x
2 1)3
演示课件
6)绘图
x (, 1) 1 (1,1)
y
2
(极大)
铅直渐近线 x 1
斜渐近线
y1x5 44
特殊点
x0 y 9
2 1
44
1 (1,3) 3 (3, )
无
0
定 义
(极小)
y
y (x 3)2
4(x 1)
lim y
x
(x)
lim 3a t 2
t 1 1 t 3
3at 1 t3
lim
t 1
3 at(1t) (1t)(1t t
2
)
a
所以笛卡儿叶形线有斜渐近线 y x a
笛卡儿 叶形线
演示课件
叶形线
演示课件
第七节
备用题 求笛卡儿叶形线 x3 y3 3axy 的渐近线 .
解: 令 y = t x , 代入原方程得曲线的参数方程 :
x
3at 1 t3
,
3at2 y 1t3 ,
当x 时t 1, 因
t 1
lim y lim 3a t 2 3a t 1 x x t1 1 t 3 1 t 3
斜渐近线
2. 函数图形的描绘
按作图步骤进行
演示课件
思考与练习
D 1.
曲线
y
1 1
ex2 ex2
(
)
(A) 没有渐近线;
(B) 仅有水平渐近线;
(C) 仅有铅直渐近线; (D) 既有水平渐近线又有铅直渐近线.
提示:
lim
x
1 1
e e
x x
2 2
1;
lim 1 x01
e e
x x
2 2
演示课件
演示课件
2 3
(极小)
例4. 描绘方程
的图形.
解: 1) y (x 3)2 , 定义域为 4(x 1)
2) 求关键点. 原方程两边对 x 求导得
2(x 3) 4 y 4 y 4xy 0
①
y x 3 2y 2(x 1)
①两边对 x 求导得 2 4 y 8y 4xy 0
y 1 4 y 2(x 1)
x x
x
b lim [ f (x) k x]
x (或 x )
演示课件
例2. 求曲线
的渐近线.
y
解:
y
x3
,
(x 3)(x 1)
lim y ,
x 3
(或 x 1)
3 O1 x
y x2
所以有铅直渐近线 x 3 及 x 1
又因
ቤተ መጻሕፍቲ ባይዱ
k
lim
x
f (x) x
lim
x
x2
x2 2x
3
b
lim [
2. 曲线 y 1 ex2 的凹区间是
( 1 , 1 )
22
,
凸区间是
( ,
1 )
2
及
(
1 , )
2
,
拐点为
(
1
1
,1e 2 )
2
,
渐近线
y 1
.
提示:
y 2 ex2 (1 2 x2 )
y
1
1
( 1 ,1 e 2 )
2
O
(
1
,1
1
e2 )
2
x
演示课件
作业
P76 14 (2); P169 2 ; 5
令 y 0 得 x 1, 3 ;
演示课件
3) 判别曲线形态
x (, 1) 1
y
0
y
y
2
(1,1)
1 (1,3) 3
无
0
定
义
0
(3, )
(极大)
(极小)
4) 求渐近线
lim y , x 1 为铅直渐近线
x1
y (x 3)2 , 4(x 1)
y
(
x 4(
3)(x x 1)2
第六节 函数图形的描绘
一、 曲线的渐近线 二、 函数图形的描绘
演示课件
一、 曲线的渐近线
定义 . 若曲线 C上的点M 沿着曲线无限地远离原点
时, 点 M 与某一直线 L 的距离趋于 0, 则称直线 L 为
曲线C 的渐近线 .
y
y f (x)
或为“纵坐标差” C M
y kxb
例如, 双曲线
L PN
演示课件
2. 斜渐近线 ( P76 题14)
若
(kx b)
(或 x )
(kx b)
lim x [ f (x) k b ] 0
x
x
x
斜渐近线 y k x b. k lim [ f (x) b ]
x x x k lim f (x)
x x
(或 x )
lim [ f (x) k b ] 0
演示课件
例3. 描绘
的图形.
解: 1) 定义域为
无对称性及周期性.
2) y x2 2x, y 2x 2,
y
令 y 0,
令 y 0,
1 O 1 2 3 x
3) x (,0) 0 (0,1) 1 (1, 2) 2 (2, )
y
0
0
y y
x 1 3
4)
y2
3
2
0
2
4 3
(极大)
(拐点)
y 0
y
y
1 2π
0
1
2πe
(极大)
(拐点)
演示课件
x 0 (0, 1) 1 (1, )
y 0
y
0
y
1 2π
1 2πe
(极大)
(拐点)
4) 求渐近线
lim y 0
x
y 0 为水平渐近线
5) 作图
y
1 2π
A
y0 O
y
1
x2
e2
2π
B
1
x
演示课件
内容小结
1. 曲线渐近线的求法
水平渐近线 ; 垂直渐近线;
有渐近线
x y0 ab
O
x
y
但抛物线
无渐近线 .
Ox
演示课件
1. 水平与铅直渐近线
若
则曲线
有水平渐近线 y b.
(或 x )
若
则曲线
有铅直渐近线 x x0 .
(或 x x0 )
y
例1. 求曲线
的渐近线 .
解: lim ( 1 2) 2 x x 1
2
x
O1
y 2 为水平渐近线;
lim( 1 2) , x 1为铅直渐近线. x1 x 1
