结构力学计算题
结构力学例题

v AF 7Pl3 60EI
此道题也可采用李兹法。设挠度曲 线 。 n
v(x) ai xi i 1
例5 用矩阵法写出下图所示连续梁单元 ①②的单元刚度矩阵,建立总刚度方 程,并进行约束处理,计算节点处的 位移。已知EI为常数,A l3 / (12EI ) 。
l
3
l
解:(1)根据结构的受力特点,将它离散 为2个单元,3个节点,并建立杆元的 局部坐标及结构的总坐标如上图所示。
结构力学例题
例1 利用梁的弯曲要素表计算下图中梁 的固定端弯矩。已知 l / (6EI) 。
解:由叠加法原理可将上述结构拆为下 列情况的组合。
q
M1
M2
ql / 3
通过查弯曲要素表有
图(a)中
1
M1l 3EI
M 2l 6EI
2
M1l 6EI
M 2l 3EI
图 (b) 中
3
1 45
ql 3 EI
M 32 0
弯矩图如下所示:
0.065ql 2
0.18ql 2
0.25ql 2
0.125ql 2
例4 用能量法求解如图所示梁的静不定 性。已知图中EI为常数,柔性系数
。 A l3 / (12EI )
解:设弹性支座处的支反力为F,则有力 的平衡关系可得弯矩分布函数,如下:
M (x) (F P)x (3P F)l (0 x l) 2
则杆元①在总坐标系中的刚度矩阵为
杆元②的局部坐标与总坐标一致,故有
A 0 0 A 0 0
0
12I l2
6I l
0
12I l2
6I
l
6I
K (2)
E l
0 A
《结构力学习题集》(上)第四章超静定结构计算——力法
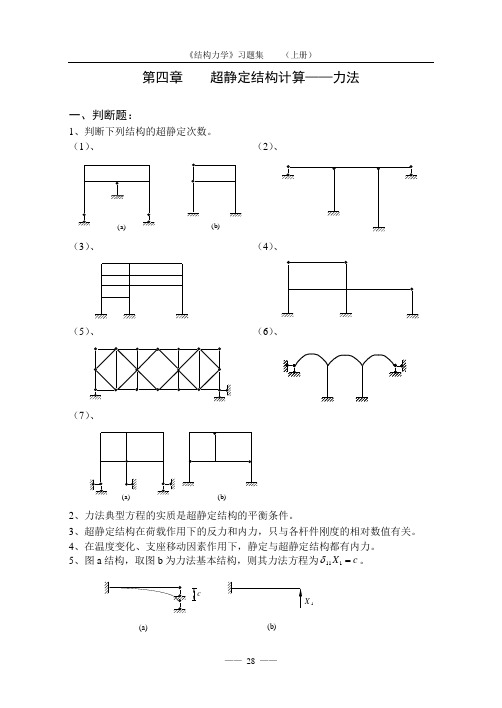
第四章 超静定结构计算——力法一、判断题:1、判断下列结构的超静定次数。
(1)、 (2)、(a )(b)(3)、 (4)、(5)、 (6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。
5、图a 结构,取图b 为力法基本结构,则其力法方程为δ111X c =。
(a)(b)X 16、图a 结构,取图b 为力法基本结构,h 为截面高度,α为线膨胀系数,典型方程中∆12122t a t t l h =--()/()。
t 21t l Ah(a)(b)X 17、图a 所示结构,取图b 为力法基本体系,其力法方程为。
(a)(b)1二、计算题:8、用力法作图示结构的M 图。
3mm9、用力法作图示排架的M 图。
已知 A = 0.2m 2,I = 0.05m 4,弹性模量为E 0。
qa a11、用力法计算并作图示结构的M 图。
ql /212、用力法计算并作图示结构的M 图。
q3 m4 m13、用力法计算图示结构并作出M 图。
E I 常数。
(采用右图基本结构。
)l 2/3l /3/3l/314、用力法计算图示结构并作M 图。
EI =常数。
3m 3m2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l lql l17、用力法计算并作图示结构M 图。
E I =常数。
18、用力法计算图示结构并作弯矩图。
161kNmmmm19、已知EI = 常数,用力法计算并作图示对称结构的M 图。
ql lqa a21、用力法作图示结构的 M 图 。
EI = 常数。
2ql22、用力法作M 图。
各杆EI 相同,杆长均为 l 。
23、用力法计算图示结构并作M 图。
EI = 常数。
4m2kN24mmm24、用力法计算并作出图示结构的M 图。
E = 常数。
20kN3m 4m 3m26、用力法计算图示结构并作M 图。
结构力学习题资料

结构力学复习题一、单选题1、①下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1正确答案(B)②下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(C)③下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(A)④下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(D)2、①分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(A)②分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(D)③分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(D)④分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(B)3、①指出下列结构的零杆个数为。
(A)2 (B)3 (C)4 (D)5正确答案(C)②指出下列结构的零杆个数为。
(A)9 (B)10 (C)11 (D)12 正确答案(C)③指出下列桁架的类型。
(A)简单桁架(B)联合桁架(C)组合桁架(D)复杂桁架正确答案(B)④指出下列桁架的类型。
(A)简单桁架(B)联合桁架(C)组合桁架(D)复杂桁架正确答案(A)⑤指出下列结构的单铰个数为。
(A)13 (B)14 (C)15 (D)16正确答案(D)4、①指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(B)②指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(C)③指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(A)④指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(B)⑤指出下列结构的超静定次数为。
结构力学计算题经典(有答案)
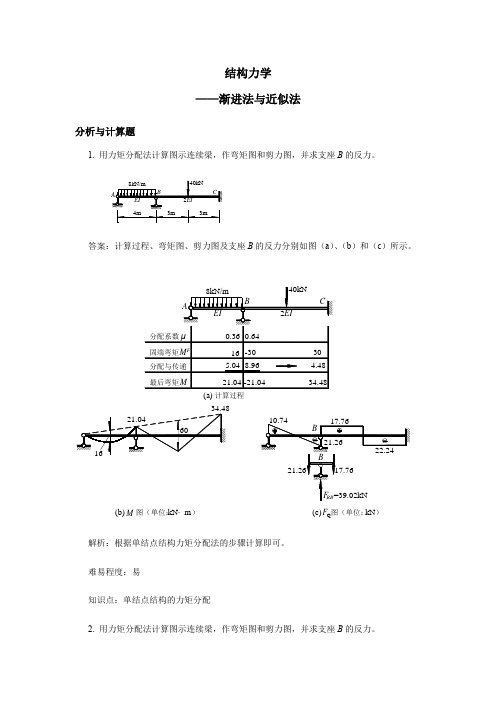
结构力学 ——渐进法与近似法分析与计算题1. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:计算过程、弯矩图、剪力图及支座B 的反力分别如图(a )、(b )和(c )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:易知识点:单结点结构的力矩分配2. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
A60kN 40kN·m EIEI B C4m4m6m(b)M 图(单位: )kN·m 图(单位: )(c)kNQ F (a)计算过程答案:图(a )为求解结点B 约束力矩的受力分析图。
计算过程、弯矩图、剪力图及支座B 的反力分别如图(b )、(c )和(d )所示。
解析:根据单结点结构力矩分配法的步骤计算即可。
难易程度:中知识点:单结点结构的力矩分配3. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:CD 段为静定悬臂梁,将其截开并暴露出截面C 的弯矩,用力矩分配法计算如图(a )所示结构。
弯矩图和剪力图如图(b )、(c )所示。
BCEIN/m2EI m3m3m40kN(b)计算过程F BM (a)图(单位: )(c)M kN·m图(单位: )Q F (d)kN10kN20kN12kN/m ABCDEI 2EI 2m 4m4m解析:根据单结点结构力矩分配法的步骤计算即可。
本题中悬臂段CD 若不切除,则可按B 、C 两个刚结点的结构进行计算。
难易程度:中知识点:单结点结构的力矩分配4. 用力矩分配法计算图示连续梁,作弯矩图和剪力图,并求支座B 的反力。
答案:AB 段为静定悬臂梁,将其截开并暴露出截面B 的弯矩,用力矩分配法计算过程如图(a )所示。
弯矩图和剪力图图(b )、(c )所示。
kNQ F (c)图(单位: )m M 图(单位: )(b)RB F =63.02kN ( )计算过程(a)mkN·10kN/m 60kN EI 2IB CD2m6m2m解析:根据单结点结构力矩分配法的步骤计算即可。
结构力学计算和分析题

三、基本计算题(本大题共4小题,每小题7分,共28分)19.计算图示桁架指定杆件a、b中的内力。
20.求图示桁架结点D的水平位移。
各杆EA相同。
21.用力矩分配法计算图示结构,并作弯矩图。
22.当行列荷载在图示位置时,利用影响线计算截面K的弯矩值。
四、分析计算题(本大题共3小题,每小题12分,共36分)23.作图示刚架的弯矩图、剪力图及轴力图。
24.计算图示结构,并作弯矩图。
EI=常数。
25.用位移法作图示结构的M图,并求支座A的水平反力。
EI=常数。
三、计算题(每小题6分,共30分)21.用位移法计算图示结构,作弯矩图。
22.用机动法画出图示静定多跨梁的弯矩M A、剪力Q A及反力R B的影响线。
23.求图示结构①单元局部坐标下的杆端力。
已知结点位移{△}=1×10-4[0.485,-1.485,0,0.515]T m,各杆EA=2×105kN,P=10kN,l=2m 。
24.不计轴向变形,求图示刚架结构刚(劲)度矩阵中K 11和K 22两个主元素。
EI=常数。
25.图示体系各柱质量不计,EI=常数,横梁EI 1=∞,简谐荷载频率θ=3ml EI 18,不计阻尼。
求最大动力弯矩值。
四、分析计算题(每小题10分,共30分)26.用力法计算图示结构,作出弯矩图。
EI=常数27.吊车荷载在简支梁AB、BC上移动,P1=P2=240kN,P3=P4=160kN,求支座反力R B的最大值。
28.图示体系各杆EI=常数。
求自振频率。
三、计算分析题(共62分)16.分析图示体系的几何组成,说明理由并作出结论。
(6分)17.作图示刚架的弯矩、剪力图。
(8分)18.求图示桁架中指定杆1、2的轴力。
(6分)19. 利用影响线,求图示梁在移动荷载作用下支座A的反力R A的最大值。
(6分)20.求图示刚架结点A的竖向位移,各杆EI=常数。
(8分)21.用力法计算图示结构,并作M图,各杆EI=常数。
结构力学练习题

1、 已知图示结构弯矩图,试作剪力图。
2、用位移法计算图示结构,作弯矩图。
(EI=常数)3、计算图示在荷载作用下的静定刚架,绘出其弯矩M 图,并求C 点的竖向位移CvΔ。
4、用位移法计算图示结构D 点水平位移Δ,EI 为常数。
L EIF P EI 1 =∞DL EIL5、用位移法计算图示刚架,并画出M图。
6、用位移法作图示结构M图。
E=常数。
7、用位移法计算图示结构,并画出弯矩图。
8、利用对称性,用力法计算下图所示超静定结构,并画出M图。
lEIBAEIEIqEIDCql9、用力法计算图示钢架,并绘制弯矩图,EI为常数。
20kN/m40kN6m6m10、用力法计算图示结构,并画出弯矩图。
11、试列出图示刚架的力法典型方程,并求出所有系数和自由项。
(EI=常数)12、下图所示超静定刚架支座A 产生逆时针转角 ,支座C 产生竖向沉降c ,并受图示荷载作用,用力法计算该刚架并画出M 图。
aAB EIEIqCac13、计算图示静定组合结构,画出梁式杆的弯矩图。
2m2m2m DAF1kN/mC2m2mEGB14、试做图示多跨静定梁的弯矩图,剪力图。
15、作 图 示 结 构 的 M 图 。
AB C a aa aF P a D E FF P16、试做图示结构的弯矩图,剪力图。
17、计算图示结构,绘弯矩图、剪力图、轴力图。
18、试作图示多跨静定梁的弯矩图、剪力图。
19、计算图示桁架指定杆件1、2、3的内力。
20、计算图示刚架A、C两截面的相对转角 AC。
结构力学动力计算习题
m
m l l l
练习题 .按先处理法求图示连续梁的刚度方程 8 .按先处理法求图示连续梁的刚度方程 (不
考虑梁的轴向变形)。 考虑梁的轴向变形)。
2kN 5 k N .m
1 2EI 2 EI
4kN 1 2 k N /m
3 EI 4
4m
4m
4m
练习题
9. 求图示结构各元的杆端力,并画出内力图。 求图示结构各元的杆端力,并画出内力图。
E = 10 kN m , θ = 20s , 5 3 k = 3 × 10 N/m, P = 5 × 10 N, W = 9.8kN
5 2 -1
Psinθ t
W 2m 2m
k
练习题 图示刚架杆自重不计,各杆EI=常数。 EI=常数 7. 图示刚架杆自重不计,各杆EI=常数。求自 振频率及振型,并画出振型图。 振频率及振型,并画出振型图。
练习题 10. 按后处理法求图示结构的结点荷载列阵 。 按后处理法求图示结构的结点荷载列阵{P}。 各杆EI=常数。 常数。 各杆 常数
4 kN 5 kN 2 6 kN /m 1
2 0 kN. m 3
4 3 kN
6
5
4m
4m
4m
m1
EI
l
m2
2EI 2EI l
练习题
5. 图示三铰刚架各杆 图示三铰刚架各杆EI=常数,杆自重不计。 常数, 常数 杆自重不计。
求自振频率与主振型。 求自振频率法。 用柔度法。
练习题
3
f11 = 1 × ( 1 × l × l × 2 × l ) × 4 = l EI 2 2 3 2 3EI l3 f 22 = f11 = f12 = f 21 = 0 3EI
结构力学自由度的计算例题及解析
1. 对于一个简单的平面桁架结构,若共有6个节点和10根构件,那么其自由度为多少?- A. 6- B. 8- C. 10- D. 122. 在一个平面梁结构中,每个支座具有多少个约束?- A. 1- B. 2- C. 3- D. 43. 计算一个刚性连接的平面框架结构的自由度时,若结构有8个节点和12根构件,自由度公式为:自由度 = 3n - 2j,其中n是节点数,j是构件数。
该结构的自由度是多少?- A. 4- B. 6- C. 8- D. 104. 一个平面结构中,假设有4个节点,6根构件,所有构件都在一个平面上,计算其自由度时需考虑:- A. 3自由度每节点,减去2自由度每构件- B. 2自由度每节点,减去1自由度每构件- C. 2自由度每节点,减去2自由度每构件- D. 3自由度每节点,减去1自由度每构件5. 对于一个三维空间的桁架结构,若有10个节点和20根构件,其自由度计算应使用的公式是:- A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 3n - 3j- D. 自由度 = 6n - 6j6. 在平面框架结构中,如果节点数为5,构件数为8,计算其自由度时,正确的自由度为: - A. 6- B. 8- C. 10- D. 127. 对于一个有10个节点和15根构件的平面结构,其自由度为:- A. 15- B. 18- D. 248. 一个简单的平面框架结构中有6个节点,8根构件,计算自由度时,如果框架是完全支撑的,结果是:- A. 3- B. 6- C. 9- D. 129. 对于一个空间框架结构,其中有5个节点和12根构件,计算自由度时所用的公式为: - A. 自由度 = 6n - 3j- B. 自由度 = 3n - 2j- C. 自由度 = 6n - 2j- D. 自由度 = 3n - 3j10. 若一个平面结构中节点数为7,构件数为10,且结构为刚性框架,计算其自由度时,结果为:- A. 5- B. 7- C. 9- D. 11。
结构力学试题及答案汇总(完整版)
. .word . .院(系) 建筑工程系 学号 三明学院 姓名 .密封线内不要答题 密封……………………………………………………………………………………………………………………………………………………结构力学试题答案汇总一、选择题(每小题3分,共18分)1. 图 示 体 系 的 几 何 组 成 为 : ( A ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬 变 ; D. 常 变 。
(第1题) (第4题)2. 静 定 结 构 在 支 座 移 动 时 , 会 产 生 : ( C )A. 力 ;B. 应 力 ;C. 刚 体 位 移 ;D. 变 形 。
3. 在 径 向 均 布 荷 载 作 用 下 , 三 铰 拱 的 合 理 轴 线 为: ( B )A .圆 弧 线 ;B .抛 物 线 ;C .悬 链 线 ;D .正 弦 曲 线 。
4. 图 示 桁 架 的 零 杆 数 目 为 : ( D )A. 6;B. 7;C. 8;D. 9。
5. 图 a 结 构 的 最 后 弯 矩 图 为 : ( A )A .图 b ;B .图 c ;C .图 d ;D .都不 对 。
6. 力 法 方 程 是 沿 基 本 未 知 量 方 向 的 : ( C ) A .力 的 平 衡 方 程 ; B .位 移 为 零 方 程 ;C .位 移 协 调 方 程 ;D .力 的 平 衡 及 位 移 为 零 方 程 。
. .word . .二、填空题(每题3分,共9分)1.从 几 何 组 成 上 讲 , 静 定 和 超 静 定 结 构 都 是___几何不变____体 系 , 前 者___无__多 余 约 束 而 后 者____有___多 余 约 束 。
2. 图 b 是 图 a 结 构 ___B__ 截 面 的 __剪力__ 影 响 线 。
3. 图 示 结 构 AB 杆 B 端 的 转 动 刚 度 为 ___i___, 分 配 系 数 为 ____1/8 ____, 传 递 系 数 为 ___-1__。
武汉理工大学专升本结构力学题库
一、计算( 每题参考分值5分)1、位移法计算图10结构。
各杆EI相同,且为常数,忽略杆件的轴向变形。
(1)写出位移法的独立基本未知量;(2)写出杆端弯矩表达式;(3)列出位移法基本方程(不需求解)。
图10正确答案:位移法(1)位移法的独立基本未知量为:(3分)(2)杆端弯矩表达式:(每项3分,共6分)(3)位移法基本方程(2分)(4分)2、位移法计算图12结构。
各杆EI=常数,忽略杆件的轴向变形。
(1)写出位移法的独立基本未知量;(2)写出杆端弯矩表达式;(3)列出位移法基本方程(不需求解)。
图12正确答案:位移法(1)位移法的独立基本未知量为:(3分)(2)杆端弯矩表达式:(每项2分,共8分)(3)位移法基本方程(4分)3、力法求图8结构。
各杆EI相同,且为常数,忽略杆件的轴向变形。
(要求写出详细的计算过程)(1)求C支座的支座反力;(2)(2)绘弯矩图。
图8正确答案:力法上图每图2分,共8分(1分)(2分)(2分)(1分)(1分)4、位移法计算图13结构。
各杆EI相同,且为常数,忽略杆件的轴向变形。
(1)写出位移法的独立基本未知量;(2)写出杆端弯矩表达式;(3)列出位移法基本方程(不需求解)。
图13正确答案:位移法(1)位移法的独立基本未知量为:(3分)(2)杆端弯矩表达式:(每项2分,共8分)(3)位移法基本方程(4分)5、图12结构受到简谐荷载作用,已知:。
EI=常数,忽略杆件的轴向变形。
求:QCA的幅值。
图12正确答案:动力学(1)自振频率(5分)(4分)(2)动力系数(3分)(3)的幅值(3分)6、图12结构受到简谐荷载作用,已知:。
柱的EI相同,且为常数,横梁的EI1为∞。
忽略杆件的轴向变形。
求:QDB的幅值。
图12正确答案:动力学(1)自振频率(5分)(4分)(2)动力系数(3分)(3)的幅值(3分)7、力矩分配法计算图10结构,并绘制弯矩图。
EI=常数,忽略杆件的轴向变形。
图10正确答案:力矩分配法(1)转动刚度(3分),分配系数(3分),固端弯矩(3分)(2)分配及传递过程(3分),弯矩图(kN·m)(3分)8、力法计算图10结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BV
B
1)虚设力状态并作M图如图a)
2)作实际位移状态的M p图如图b)
3)求△BV
)
(
3
8800
)4
4
160
(
1
)4
2
1
20
4
3
2
4
3
2
160
4
2
1
(
2
1
↓
=
⨯
⨯
+
⨯
⨯
⨯
⨯
-
⨯
⨯
⨯
⨯
=
=
∆∑⎰
EI
EI
EI
dx
EI
M
M
P
BV
4、用力法计算图示刚架,并作M图。
1)力法的基本结构如图(a)
2)力法的典型方程
P1
1
11
=
+Δ
X
δ
3)作1
M、
P
M图如图(b)(c),
并求系数及由项
2
1
11
1
1
144
810
P
P
M
dx
EI EI
M M
Δdx
EI EI
δ==
==
∑⎰
∑⎰
4)解力法的典型方程:
X1=
5)叠加法作M图1
1P
M M X M
=+
如图(d)
p
4
4
M图
160
160
20
160
b) M p图(kN·m)
11EI
EI I E 144
)636(1)6326621(2111=
⨯⨯⨯+⨯⨯⨯⨯⨯⋅=
δ
(4)求P 1∆
)]320761986207231982(6
3
)1983321[(211⨯+⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯⋅-=
∆I E P 63)2079(
1
1⨯⨯+⨯⨯-75.3759-=
(4)求1X
kN X X P
P 11.26144
75
.3759011
111111==
∆-
=⇒=∆+δδ
(5)画M 图
P P M M M X M M +⨯=+=11.26111
解:1)力法的基本结构如图(a )
2)力法的典型方程
0P 1111=+ΔX δ
3)作1N 、P N 图,并求系数及由项
EA
Pl
l EA N N ΔEA l
l EA N P P )221()244(112
111+-
=⨯=+=
⨯=∑∑δ 4)解力法的典型方程: X 1= P
5)叠加法作N 图;P N X N
N +=11如图d)
b) 1N 图
d)N 图
322/111=+=
Aa μ,31
2/112/1=+=AE μ
33.1314031
3122=⨯⨯==ql M Aa
67.614061
6122=⨯⨯==ql M aA
67.10628031
3122-=⨯⨯-=-=ql M AE
33.532806
1
6122-=⨯⨯-=-=ql M EA
计算过程:
P N P N AB AB 202-=⇒=+
③取截面Ⅰ—Ⅰ
(4)画弯矩图P M M M +∆=11
解:1)位移法的基本结构如图(a )
2)位移法的典型方程:
0P 1111=+R Z r
3)作1M 、P M 图如图 (b )(c )并求系数及由项
1110r i = 2118
P R ql =-
4)解位移法典型方程
2
180ql Z i
=
5)叠加法作M 图如图(d )
P M Z M M +=11
5、用力矩分配法作图示对称刚架的M 图。
EI=常数。
(18分)
31211=+=
Aa μ,32212=+=AE μ 33.1314031
3122=⨯⨯==ql M Aa
67.614061
6122=⨯⨯==ql M aA
67.26280121
12122-=⨯⨯-=-=ql M AE
67.2628012
1
12122=⨯⨯==ql M EA
(3)计算过程:。
