高考数学《立体几何》判断命题题型总汇
2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)

2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)1.(2022·天津·统考高考真题)直三棱柱111ABC A B C -中,112,,AA AB AC AA AB AC AB ===⊥⊥,D 为11A B 的中点,E 为1AA 的中点,F 为CD 的中点.(1)求证://EF 平面ABC ;(2)求直线BE 与平面1CC D 所成角的正弦值; (3)求平面1ACD 与平面1CC D 所成二面角的余弦值. 【解析】(1)证明:在直三棱柱111ABC A B C -中,1AA ⊥平面111A B C ,且AC AB ⊥,则1111AC A B ⊥以点1A 为坐标原点,1A A 、11A B 、11AC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()2,0,0A 、()2,2,0B 、()2,0,2C 、()10,0,0A 、()10,0,2B 、()10,0,2C 、()0,1,0D 、()1,0,0E 、11,,12F ⎛⎫⎪⎝⎭,则10,,12EF ⎛⎫= ⎪⎝⎭, 易知平面ABC 的一个法向量为()1,0,0m =,则0EF m ⋅=,故EF m ⊥,EF ⊄平面ABC ,故//EF 平面ABC .(2)()12,0,0C C =,()10,1,2C D =−,()1,2,0EB =,设平面1CC D 的法向量为()111,,u x y z =,则111112020u C C x u C D y z ⎧⋅==⎪⎨⋅=−=⎪⎩,取12y =,可得()0,2,1u =,4cos ,5EB u EB u EB u⋅<>==⋅. 因此,直线BE 与平面1CC D 夹角的正弦值为45.(3)()12,0,2AC =,()10,1,0A D =, 设平面1ACD 的法向量为()222,,v x y z =,则122122200v AC x z v A D y ⎧⋅=+=⎪⎨⋅==⎪⎩,取21x =,可得()1,0,1v =−,则1cos ,5u v u v u v⋅<>==−=⨯⋅因此,平面1ACD 与平面1CC D 2.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【解析】(1)因为AD CD =,E 为AC 的中点,所以AC DE ⊥; 在ABD △和CBD △中,因为,,B A C D CD ADB DB DB D ∠=∠==,所以ABD CBD ≌△△,所以AB CB =,又因为E 为AC的中点,所以AC BE ⊥; 又因为,DE BE ⊂平面BED ,DE BE E ⋂=,所以AC ⊥平面BED ,因为AC ⊂平面ACD ,所以平面BED ⊥平面ACD .(2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED , 所以AC EF ⊥,所以1=2AFC S AC EF ⋅△, 当EF BD ⊥时,EF 最小,即AFC △的面积最小. 因为ABD CBD ≌△△,所以2CB AB ==, 又因为60ACB ∠=︒,所以ABC 是等边三角形, 因为E 为AC 的中点,所以1AE EC ==,BE 因为AD CD ⊥,所以112DE AC ==, 在DEB 中,222DE BE BD +=,所以BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz −,则()()()1,0,0,,0,0,1A B D ,所以()()1,0,1,AD AB =−=−, 设平面ABD 的一个法向量为(),,n x y z =,则00n AD x z n AB x ⎧⋅=−+=⎪⎨⋅=−+=⎪⎩,取y =()3,3,3n =, 又因为()31,0,0,4C F ⎛⎫− ⎪ ⎪⎝⎭,所以31,4CF ⎛⎫= ⎪ ⎪⎝⎭,所以cos ,21n CF n CF n CF⋅===设CF 与平面ABD 所成的角的正弦值为02πθθ⎛⎫≤≤ ⎪⎝⎭,所以4sin cos ,7nCF θ==所以CF 与平面ABD3.(2022·浙江·统考高考真题)如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE ∠=∠=︒,二面角F DC B −−的平面角为60︒.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ⊥;(2)求直线BM 与平面ADE 所成角的正弦值.【解析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H . ∵四边形ABCD 和EFCD 都是直角梯形,//,//,5,3,1AB DC CD EF AB DC EF ===,60BAD CDE ∠=∠=︒,由平面几何知识易知,2,90DG AH EFC DCF DCB ABC ==∠=∠=∠=∠=︒,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt EGD 和Rt DHA ,EG DH == ∵,DC CF DC CB ⊥⊥,且CF CB C ⋂=,∴DC ⊥平面,BCF BCF ∠是二面角F DC B −−的平面角,则60BCF ∠=, ∴BCF △是正三角形,由DC ⊂平面ABCD ,得平面ABCD ⊥平面BCF ,∵N 是BC 的中点,∴FN BC ⊥,又DC ⊥平面BCF ,FN ⊂平面BCF ,可得FN CD ⊥,而BC CD C ⋂=,∴FN ⊥平面ABCD ,而AD ⊂平面ABCD FN AD ∴⊥.(2)因为FN ⊥平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点, NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz −,设(3,(1,0,3)A B D E,则32M ⎛⎫ ⎪ ⎪⎝⎭,333,,,(2,23,0),(2,22BM AD DE ⎛⎫∴=−=−−=− ⎪ ⎪⎝⎭ 设平面ADE 的法向量为(,,)nx y z =由00n AD n DE ⎧⋅=⎨⋅=⎩,得20230x x z ⎧−−=⎪⎨−+=⎪⎩,取(3,n =−,设直线BM 与平面ADE 所成角为θ,∴3||sin cos ,|||3n BM n BM n BMθ⋅=〈〉====⋅4.(2022·全国·统考高考真题)如图,PO 是三棱锥−P ABC 的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B −−的正弦值. 【解析】(1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥−P ABC 的高,所以PO ⊥平面ABC ,,AO BO ⊂平面ABC , 所以PO AO ⊥、PO BO ⊥,又PA PB =,所以POA POB ≅△△,即OA OB =,所以OAB OBA ∠=∠,又AB AC ⊥,即90BAC ∠=︒,所以90OAB OAD ∠+∠=︒,90OBA ODA ∠+∠=︒, 所以ODA OAD ∠=∠所以AO DO =,即AO DO OB ==,所以O 为BD 的中点,又E 为PB 的中点,所以//OE PD , 又OE ⊄平面PAC ,PD ⊂平面PAC , 所以//OE 平面PAC(2)过点A 作//Az OP ,如图建立平面直角坐标系, 因为3PO =,5AP =,所以4OA =,又30OBA OBC ∠=∠=︒,所以28BD OA ==,则4=AD,AB = 所以12AC =,所以()O,()B,()P ,()0,12,0C ,所以32E ⎛⎫ ⎪⎝⎭,则332AE ⎛⎫= ⎪⎝⎭,()43,0,0AB =,()0,12,0AC =,设平面AEB 的法向量为(),,n x y z =,则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩,令2z =,则=3y −,0x =,所以()0,3,2n =−;设平面AEC 的法向量为(),,m a b c =,则33302120m AE a bc m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩,令a =6c =−,0b =,所以()3,0,6m =−;所以cos ,13n m n m n m⋅−===设二面角C AE B −−的大小为θ,则43cos cos ,=13n m θ=, 所以11sin 13θ=,即二面角C AE B −−的正弦值为1113.5.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求三棱锥F ABC −的体积.【解析】(1)由于AD CD =,E 是AC 的中点,所以AC DE ⊥.由于AD CDBD BD ADB CDB =⎧⎪=⎨⎪∠=∠⎩,所以ADB CDB ≅△△,所以AB CB =,故AC BD ⊥,由于DE BD D ⋂=,,DE BD Ì平面BED , 所以AC ⊥平面BED ,由于AC ⊂平面ACD ,所以平面BED ⊥平面ACD . (2)[方法一]:判别几何关系依题意2AB BD BC ===,60ACB ∠=︒,三角形ABC 是等边三角形,所以2,1,AC AE CE BE ===由于,AD CD AD CD =⊥,所以三角形ACD 是等腰直角三角形,所以1DE =. 222DE BE BD +=,所以DE BE ⊥,由于AC BE E ⋂=,,AC BE ⊂平面ABC ,所以DE ⊥平面ABC . 由于ADB CDB ≅△△,所以FBA FBC ∠=∠,由于BF BF FBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩,所以FBA FBC ≅,所以AF CF =,所以EF AC ⊥, 由于12AFCSAC EF =⋅⋅,所以当EF 最短时,三角形AFC 的面积最小 过E 作EF BD ⊥,垂足为F ,在Rt BED △中,1122BE DE BD EF ⋅⋅=⋅⋅,解得EF =所以13,222DF BF DF ===−=, 所以34BF BD =过F 作FH BE ⊥,垂足为H ,则//FH DE ,所以FH ⊥平面ABC ,且34FH BF DE BD ==, 所以34FH =,所以111323324F ABC ABCV SFH −=⋅⋅=⨯⨯=[方法二]:等体积转换AB BC =,60ACB ∠=︒,2AB =ABC ∴∆是边长为2的等边三角形,BE ∴=连接EFADB CDB AF CF EF ACBED EF BD ∆≅∆∴=∴⊥∴∆⊥∆在中,当时,AFC 面积最小222,,2,,BED EF AD CD AD CD AC E AC DE BE BD BE EDBE DE EF BD BD ⊥==∴+=∴⊥⋅⊥∆==为中点DE=1若在中,32113222BEFBF S BF EF ∆∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC −−−∆∴=+=⋅=6.(2022·全国·统考高考真题)在四棱锥P ABCD −中,PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP ====∥(1)证明:BD PA ⊥;(2)求PD 与平面PAB 所成的角的正弦值.【解析】(1)证明:在四边形ABCD 中,作DE AB ⊥于E ,CF AB ⊥于F , 因为//,1,2CD AB AD CD CB AB ====, 所以四边形ABCD 为等腰梯形, 所以12AE BF ==,故DE =BD = 所以222AD BD AB +=, 所以AD BD ⊥,因为PD ⊥平面ABCD ,BD ⊂平面ABCD , 所以PD BD ⊥, 又=PD AD D ⋂, 所以BD ⊥平面PAD , 又因为PA ⊂平面PAD , 所以BD PA ⊥;(2)如图,以点D 为原点建立空间直角坐标系,BD =则()()(1,0,0,,A B P ,则()()(1,0,3,0,3,3,AP BP DP =−=−=,设平面PAB 的法向量(),,n x y z =,则有0{30n AP x n BP ⋅=−=⋅=−=,可取()3,1,1n =, 则5cos ,5n DPn DP n DP ⋅==所以PD 与平面PAB7.(2022·北京·统考高考真题)如图,在三棱柱111ABC A B C -中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N 分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值.条件①:AB MN ⊥;条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.【解析】(1)取AB 的中点为K ,连接,MK NK ,由三棱柱111ABC A B C -可得四边形11ABB A 为平行四边形,而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B ,而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B ,而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B ,(2)因为侧面11BCC B 为正方形,故1CB BB ⊥,而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A ,平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A ,因为//NK BC ,故NK ⊥平面11ABB A ,因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =,故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥,所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯. 若选②,因为//NK BC ,故NK ⊥平面11ABB A ,而KM ⊂平面MKN , 故NK KM ⊥,而11,1B M BK NK ===,故1B M NK =,而12B B MK ==,MB MN =,故1BB M MKN ≅,所以190BB M MKN ∠=∠=︒,故111A B BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯.8.(2022·全国·统考高考真题)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C −−的正弦值. 【解析】(1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h , 则111111112211433333A A BC A A ABC A ABC AB BC C C B V S h h V S A A V −−−=⋅===⋅==,解得h =所以点A 到平面1A BC (2)取1A B 的中点E ,连接AE ,如图,因为1AA AB =,所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =, 且AE ⊂平面11ABB A ,所以⊥AE 平面1A BC , 在直三棱柱111ABC A B C -中,1BB ⊥平面ABC , 由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥,又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A , 所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB ==,1A B =2BC =, 则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1AC 的中点()1,1,1D , 则()1,1,1BD =,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩, 可取()1,0,1m =−,设平面BDC 的一个法向量(),,n a b c =,则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩, 可取()0,1,1n =−r , 则11cos ,22m nm n m n ⋅===⨯⋅,所以二面角A BD C −−=本课结束。
高三高考数学总复习《立体几何》题型归纳与汇总

(3)当 PA// 平面 BDE 时, PA 平面 PAC ,且平面 PAC 平面 BDE DE ,可得 PA//DE .由 D 是 AC 边的中 点知, E 为 PC 边的中点.故而 ED 1 PA 1, ED∥PA ,因为 PA 平面 ABC ,所以 ED 平面 BDC .
2
由 AB BC 2 ,AB BC ,D 为 AC 边中点知,BD CD 2. 又 BD AC ,有 BD DC ,即 BDC 90.
3 【解析】(1)∵ PA PD, N 为 AD 的中点,∴ PN AD, ∵底面 ABCD为菱形, BAD 60 ,∴ BN AD, ∵ PN BN N ,∴ AD 平面 PNB . (2)∵ PN PD AD 2 , ∴ PN NB 3 , ∵平面 PAD 平面 ABCD,平面 PAD 平面 ABCD AD , PN AD, ∴ PN 平面 ABCD, ∴ PN NB ,
【易错点】 外接球球心位置不好找 【思维点拨】 应用补形法找外接球球心的位置
题型四 立体几何的计算
例 1 如图,已知三棱锥的底面是直角三角形,直角 边边长分别为 3 和 4 ,过直角顶点的侧棱长为 4 ,且 垂直于底面,该三棱锥的主视图是 ( )
【答案】 B 【解析】显然由空间直角坐标系可知,该几何体在 xoy 面内的点保持不动,在 y 轴上的点在 xoy 面内的射影为坐标原 点,所以该几何体的主视图就是其在面 xoy 面的表面图形,即主视图应为高为 4 ,底面边长为 3 的直角三角形.故选 B.
以 PA BD . (2)因为 AB BC , AB BC , D 为线段 AC 的中点,所以在等腰 Rt△ABC 中, BD AC .又 由(1)可知, PA BD,PA AC A,所以 BD 平面 PAC .由 E 为线段 PC 上一点,则 DE 平面 PAC ,
立体几何7大题型汇编

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高中数学高考总复习立体几何平行与垂直的判断习题及详解

高中数学高考总复习立体几何平行与垂直的判断习题及详解一、选择题1.(文)(09·福建)设m,n是平面α内的两条不同直线;l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是()A.m∥β且l1∥αB.m∥l1且n∥l2C.m∥β且n∥βD.m∥β且n∥l2[答案] B[解析]如图(1),α∩β=l,m∥l,l1∥l,满足m∥β且l1∥α,故排除A;如图(2),α∩β=l,m∥n∥l,满足m∥β,n∥β,故排除C.在图(2)中,m∥n∥l∥l2满足m∥β,n∥l2,故排除D,故选B.[点评]∵l1与l2相交,m∥l1,n∥l2,∴m与n相交,由面面平行的判定定理可知α∥β;但当m、n⊂α,l1,l2⊂β,l1与l2相交,α∥β时,如图(3),得不出m∥l1且n∥l2.(理)设a,b是两条直线,α,β是两个平面,则a⊥b的一个充分条件是()A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β[答案] C[解析]对于A,如图正方体α、β分别为平面ABCD与平面ADD1A1,a、b分别为直线B1B和C1C.a与b也可能平行,对于B,∵a⊥α,α∥β,∴a⊥β,又b⊥β,∴a∥b,对于D,a与b也可能平行,故选C.2.(2010·郑州检测)已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题.如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有()A.0个B.1个C.2个D.3个[答案] C[解析]依题意得,命题“a∥b,且a⊥γ⇒b⊥γ”是真命题(由“若两条平行线中的一条与一个平面垂直,则另一条也与这个平面垂直”可知);命题“a∥β,且a⊥c⇒β⊥c”是假命题(直线c可能位于平面β内,此时结论不成立);命题“α∥b,且α⊥c⇒b⊥c”是真命题(因为α∥b,因此在平面α内必存在直线b1∥b;又α⊥c,因此c∥b1,c⊥b).综上所述,其中真命题共有2个,选C.3.(2010·东北三校模拟)正方体ABCD -A 1B 1C 1D 1中,M ,N ,P 分别为A 1B 1,CD ,B 1C 1的中点,则下列命题正确的是( )A .AM 与PC 是异面直线B .AM ⊥PC C .AM ∥平面BC 1ND .四边形AMC 1N 为正方形 [答案] C[解析] 连接MP ,AC ,A 1C 1,AM ,C 1N ,由题易知MP ∥A 1C 1∥AC ,且MP =12AC ,所以AM 与PC 是相交直线,假设AM ⊥PC ,∵BC ⊥平面ABB 1A 1,∴BC ⊥AM ,∴AM ⊥平面BCC 1B 1,又AB ⊥平面BCC 1B 1矛盾,∴AM 与PC 不垂直.因为AM ∥C 1N ,C 1N ⊂平面BC 1N ,所以AM ∥平面BC 1N .又易得四边形AMC 1N 为菱形而不是正方形,故选C.4.(文)对两条不相交的空间直线a 与b ,必存在平面α,使得( ) A .a ⊂α,b ⊂α B .a ⊂α,b ∥α C .a ⊥α,b ⊥αD .a ⊂α,b ⊥α[答案] B[解析] a 、b 异面时,A 错,C 错;若D 正确,则必有a ⊥b ,故排除A 、C 、D ,选B.(理)设a 、b 为两条直线,α、β为两个平面.下列四个命题中,正确的命题是( ) A .若a 、b 与α所成的角相等,则a ∥b B .若a ∥α,b ∥β,α∥β,则a ∥b C .若a ⊂α,b ⊂β,a ∥b ,则α∥β D .若a ⊥α,b ⊥β,α⊥β,则a ⊥b [答案] D[解析] 若直线a 、b 与α成等角,则a 、b 平行、相交或异面;对选项B ,如a ∥α,b ∥β,α∥β,则a 、b 平行、相交或异面;对选项C ,若a ⊂α,b ⊂β,a ∥b ,则α、β平行或相交;对选项D ,由⎭⎪⎬⎪⎫a ⊥αβ⊥α⇒a ∥β或a ⊂β,无论哪种情形,由b ⊥β都有b ⊥a .,故选D. 5.一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB ⊥EF ②AB 与CM 成60°③EF 与MN 是异面直线④MN ∥CD 其中正确的是( )A.①②B.③④C.②③D.①③[答案] D[解析]本题考查学生的空间想象能力,将其还原成正方体如图所示,AB⊥EF,EF与MN是异面直线,AB∥CM,MN⊥CD.只有①③正确,故选D.6.(文)(2010·山东潍坊)已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是()A.若α⊥γ,α⊥β,则γ∥βB.若m∥n,m⊂α,n⊂β,则α∥βC.若m∥n,m∥α,则n∥αD.若m∥n,m⊥α,n⊥β,则α∥β[答案] D[解析]对于选项A,两平面β、γ同垂直于平面α,平面β与平面γ可能平行,也可能相交;对于选项B,平面α、β可能平行,也可能相交;对于选项C,直线n可能与平面α平行,也可能在平面α内;对于选项D,∵m∥n,m⊥α,∴n⊥α,又n⊥β,∴α∥β,故选D.(理)(2010·曲师大附中)已知两个不同的平面α,β和两条不重合的直线a,b,则下列四个命题中为真命题的是()A.若a∥b,b⊂α,则a∥αB.若α⊥β,α∩β=b,a⊥b,则a⊥βC.若a⊂α,b⊂α,a∥β,b∥β,则α∥βD.若α∥β,a⊄α,a⊄β,a∥α,则a∥β[答案] D[解析]选项A中,直线a可能在平面α内;选项B中,直线a可能在平面β内;选项C 中,直线a ,b 为相交直线时命题才成立.7.(2010·江苏南通)在正方体ABCD -A 1B 1C 1D 1中,P 、Q 分别是棱AA 1、CC 1的中点,则过点B 、P 、Q 的截面是( )A .邻边不等的平行四边形B .菱形但不是正方形C .邻边不等的矩形D .正方形 [答案] B[解析] 设正方体棱长为1,连结D 1P ,D 1Q ,则易得PB =PQ =D 1P =D 1Q =52,取D 1D 的中点M ,则D 1P 綊AM 綊BQ ,故截面为四边形PBQD 1,它是一个菱形,又PQ =AC =2,∴∠PBQ 不是直角,故选B.8.(文)(2010·山东日照、聊城模考)已知直线l 、m ,平面α、β,且l ⊥α,m ⊂β,给出下列四个命题:①若α∥β,则l ⊥m ;②若l ⊥m ,则α∥β;③若α⊥β,则l ∥m ;④若l ∥m ,则α⊥β; 其中真命题是( ) A .①② B .①③ C .①④D .②④[答案] C [解析][点评] 如图,α∩β=m ,则l ⊥m ,故(2)假;在上述图形中,当α⊥β时,知③假.(理)(2010·福建福州市)对于平面α和共面的直线m ,n ,下列命题是真命题的是( ) A .若m ,n 与α所成的角相等,则m ∥n B .若m ∥α,n ∥α,则m ∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n[答案] D[解析]正三棱锥P-ABC的侧棱P A、PB与底面成角相等,但P A与PB相交应排除A;若m∥α,n∥α,则m与n平行、相交或异面,应排除B;若m⊥α,m⊥n,则n∥α或n⊂α,应排除C.∵m、n共面,设经过m、n的平面为β,∵m⊂α,∴α∩β=m,∵n∥α,∴n∥m,故D正确.9.(文)(2010·北京顺义一中月考)已知l是直线,α、β是两个不同平面,下列命题中的真命题是()A.若l∥α,l∥β,则α∥βB.若α⊥β,l∥α,则l⊥βC.若l⊥α,l∥β,则α⊥βD.若l∥α,α∥β,则l∥β[答案] C[解析]如图在正方体ABCD-A1B1C1D1中,取平面ABD1A1为α,平面ABCD为β,B1C1为l,则排除A、B;又取平面ADD1A1为α,平面BCC1B1为β,B1C1为l,排除D.(理)(2010·广东罗湖区调研)已知相异直线a,b和不重合平面α,β,则a∥b的一个充分条件是()A.a∥α,b∥αB.a∥α,b∥β,α∥βC.a⊥α,b⊥β,α∥βD.α⊥β,a⊥α,b∥β[答案] C[解析]a∥α,b∥α时,a与b可相交可异面也可平行,故A错;a∥α,b∥β,α∥β时,a与b可异面,故B错;由α⊥β,a⊥α得,a∥β或a⊂β,又b∥β,此时a与b可平行也可异面,排除D.10.(2010·日照实验高中)如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,AB =1,M ,N 分别在AD 1,BC 上移动,且始终保持MN ∥平面DCC 1D 1,设BN =x ,MN =y ,则函数y =f (x )的图象大致是( )[答案] C[解析] 过M 作ME ⊥AD 于E ,连接EN ,则平面MEN ∥平面DCC 1D 1,所以BN =AE =x (0≤x <1),ME =2x ,MN 2=ME 2+EN 2,则y 2=4x 2+1,y 2-4x 2=1(0≤x <1,y >0),图象应是焦点在y 轴上的双曲线的一部分.故选C.二、填空题11.(文)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,E 、F 、G 、H 分别是棱CC 1、C 1D 1、D 1D 、DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足条件________时,有MN ∥平面B 1BDD 1.[答案] M ∈线段FH[解析] 因为HN ∥BD ,HF ∥DD 1,所以平面NHF ∥平面B 1BDD 1,又平面NHF ∩平面EFGH =FH .故线段FH 上任意点M 与N 相连,有MN ∥平面B 1BDD 1,故填M ∈线段FH .(理)(2010·南充市模拟)已知两异面直线a ,b 所成的角为π3,直线l 分别与a ,b 所成的角都是θ,则θ的取值范围是________.[答案] [π6,π2]12.在四面体ABCD 中,M 、N 分别是△ACD 、△BCD 的重心,则四面体的四个面中与MN 平行的是________.[答案] 面ABC 和面ABD[解析] 连结AM 并延长交CD 于点E ,∵M 为△ACD 的重心,∴E 为CD 的中点, 又N 为△BCD 的重心,∴B 、N 、E 三点共线, 由EM MA =EN NB =12得MN ∥AB , 因此MN ∥平面ABC ,MN ∥平面ABD .13.如图是一正方体的表面展开图,B 、N 、Q 都是所在棱的中点,则在原正方体中, ①AB 与CD 相交;②MN ∥PQ ;③AB ∥PE ;④MN 与CD 异面;⑤MN ∥平面PQC . 其中真命题的序号是________.[答案] ①②④⑤[解析] 将正方体还原后如图,则N 与B 重合,A 与C 重合,E 与D 重合,∴①、②、④、⑤为真命题.14.如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为a ,点P 是棱AD 上一点,且AP =a3,过B 1,D 1,P 的平面交底面ABCD 于PQ ,Q 在直线CD 上,则PQ =________.[答案]223a [解析] ∵B 1D 1∥平面ABCD ,平面B 1D 1P ∩平面ABCD =PQ ,∴B 1D 1∥PQ , 又B 1D 1∥BD ,∴BD ∥PQ ,设PQ ∩AB =M ,∵AB ∥CD ,∴△APM ∽△DPQ ,∴PQ PM =PDAP=2,即PQ =2PM , 又△APM ∽△ADP ,∴PM BD =AP AD =13,∴PM =13BD ,又BD =2a ,∴PQ =223a .三、解答题15.(文)(2010·南京调研)如图,在四棱锥E -ABCD 中,四边形ABCD 为平行四边形,BE =EC ,AE ⊥BE ,M 为CE 上一点,且BM ⊥平面ACE .(1)求证:AE ⊥BC ;(2)如果点N 为线段AB 的中点,求证:MN ∥平面ADE .[解析] (1)因为BM ⊥平面ACE ,AE ⊂平面ACE ,所以BM ⊥AE .因为AE ⊥BE ,且BE ∩BM =B ,BE 、BM ⊂平面EBC ,所以AE ⊥平面EBC . 因为BC ⊂平面EBC ,所以AE ⊥BC . (2)解法1:取DE 中点H ,连接MH 、AH .因为BM ⊥平面ACE ,EC ⊂平面ACE ,所以BM ⊥EC . 因为BE =BC ,所以M 为CE 的中点. 所以MH 为△EDC 的中位线,所以MH 綊12DC .因为四边形ABCD 为平行四边形,所以DC 綊AB . 故MH 綊12AB .因为N 为AB 的中点,所以MH 綊AN .所以四边形ANMH 为平行四边形,所以MN ∥AH . 因为MN ⊄平面ADE ,AH ⊂平面ADE , 所以MN ∥平面ADE .解法2:取EB 的中点F ,连接MF 、NF .因为BM ⊥平面ACE ,EC ⊂平面ACE ,所以BM ⊥EC . 因为BE =BC ,所以M 为CE 的中点,所以MF ∥BC .因为N 为AB 的中点,所以NF ∥AE , 因为四边形ABCD 为平行四边形, 所以AD ∥BC .所以MF ∥AD .因为NF 、MF ⊄平面ADE ,AD 、AE ⊂平面ADE , 所以NF ∥平面ADE ,MF ∥平面ADE . 因为MF ∩NF =F ,MF 、NF ⊂平面MNF , 所以平面MNF ∥平面ADE .因为MN ⊂平面MNF ,所以MN ∥平面ADE .(理)(2010·厦门市质检)如图所示的几何体中,△ABC 为正三角形,AE 和CD 都垂直于平面ABC ,且AE =AB =2,CD =1,F 为BE 的中点.(1)若点G 在AB 上,试确定G 点位置,使FG ∥平面ADE ,并加以证明;(2)在(1)的条件下,求三棱锥D -ABF 的体积. [解析] (1)当G 是AB 的中点时,GF ∥平面ADE . ∵G 是AB 的中点,F 是BE 的中点, ∴GF ∥AE ,又GF ⊄平面ADE ,AE ⊂平面ADE , ∴GF ∥平面ADE . (2)连接CG ,由(1)可知: GF ∥AE ,且GF =12AE .又AE ⊥平面ABC ,CD ⊥平面ABC ,∴CD ∥AE , 又CD =12AE ,∴GF ∥CD ,GF =CD ,∴四边形CDFG 为平行四边形, ∴DF ∥CG ,且DF =CG .又∵AE ⊥平面ABC ,CG ⊂平面ABC ,∴AE ⊥CG . ∵△ABC 为正三角形,G 为AB 的中点, ∴CG ⊥AB ,又AB ∩AE =A ,∴CG ⊥平面ABE . 又CG ∥DF ,且CG =DF ,∴DF 为三棱锥D -ABF 的高,且DF = 3. 又AE ⊥平面ABC ,AB ⊂平面ABC ,∴AE ⊥AB . ∵在Rt △ABE 中,AB =AE =2,F 为BE 的中点,∴S △ABF =12S △ABE =12×12×2×2=1.∴V D -ABF =13S △ABF ·DF =13×1×3=33,∴三棱锥D -ABF 的体积为33. 16.(文)(2010·安徽合肥质检)如图,PO ⊥平面ABCD ,点O 在AB 上,EA ∥PO ,四边形ABCD 为直角梯形,BC ⊥AB ,BC =CD =BO =PO ,EA =AO =12CD .(1)求证:BC ⊥平面ABPE ;(2)直线PE 上是否存在点M ,使DM ∥平面PBC ,若存在,求出点M ;若不存在,说明理由.[解析] (1)∵PO ⊥平面ABCD , BC ⊂平面ABCD ,∴BC ⊥PO ,又BC ⊥AB ,AB ∩PO =O ,AB ⊂平面ABP ,PO ⊂平面ABP ,∴BC ⊥平面ABP , 又EA ∥PO ,AO ⊂平面ABP , ∴EA ⊂平面ABP ,∴BC ⊥平面ABPE . (2)点E 即为所求的点,即点M 与点E 重合. 取PO 的中点N ,连结EN 并延长交PB 于F , ∵EA =1,PO =2,∴NO =1,又EA 与PO 都与平面ABCD 垂直,∴EF ∥AB , ∴F 为PB 的中点,∴NF =12OB =1,∴EF =2,又CD =2,EF ∥AB ∥CD ,∴四边形DCFE 为平行四边形,∴DE ∥CF , ∵CF ⊂平面PBC ,DE ⊄平面PBC , ∴DE ∥平面PBC .∴当M 与E 重合时即可.(理)在长方体ABCD -A 1B 1C 1D 1中,O 为底面正方形的中心,过A 1、C 1、B 三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD -A 1C 1D 1及其三视图.(1)求证:D1O∥平面A1BC1;(2)是否存在过点A1与直线DC1垂直的平面A1PQ,与线段BC1交于点P,与线段CC1交于点Q?若存在,求出线段PQ的长;若不存在,请说明理由.[分析]要证D1O∥平面A1BC1,∵O为DB的中点,∴取A1C1中点E,只须证D1E綊OB,或利用长方体为正四棱柱的特性,证明平面ACD1∥平面A1C1B,假设存在平面A1PQ ⊥DC1,利用正四棱柱中,BC⊥平面DCC1D1,故有BC⊥DC1,从而平面A1PQ与平面BCC1的交线PQ⊥DC1,故只须在面DCC1D1的边CC1上寻找点Q,使D1Q⊥DC1即可.[解析](1)连接AC,AD1,D1C,易知点O在AC上.D1、四边形A1D1CB均为平行四边根据长方体的性质得四边形ABC Array 1形,∴AD1∥BC1,A1B∥D1C,又∵AD1⊄平面A1C1B,BC1⊂平面A1C1B,∴AD1∥平面A1C1B,同理D1C∥平面A1BC1,又∵D1C∩AD1=D1,∴根据面面平行的判定定理知平面ACD1∥平面A1BC1.∵D1O⊂平面ACD1,∴D1O∥平面A1BC1.(2)假设存在过点A1与直线DC1垂直的平面A1PQ,与线段BC1交于点P,与线段CC1交于点Q.D,过点D1作C1D的垂线交C1C于点Q,过点Q作PQ连接C Array 1∥BC交BC1于点P,连接A1P,A1Q.∵C1D⊥D1Q,C1D⊥A1D1,D1Q∩A1D1=D1,∴C1D⊥平面A1D1Q.∵A1Q⊂平面A1D1Q,∴C1D⊥A1Q.∵PQ∥BC∥A1D1,∴C1D⊥PQ,∵A1Q∩PQ=Q,∴C1D⊥平面A1PQ.∴存在过点A1与直线DC1垂直的平面A1PQ,与线段BC1交于点P,与线段CC1交于点Q.在矩形CDD 1C 1中,∵Rt △D 1C 1Q ∽Rt △C 1CD ,∴C 1Q CD =D 1C 1C 1C ,结合三视图得C 1Q 2=24,∴C 1Q =1. ∵PQ ∥BC ,∴PQ BC =C 1Q CC 1=14,∴PQ =14BC =12. 17.(文)(2010·东北师大附中)如图所示,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为DD 1、DB 的中点.(1)求证:EF ∥平面ABC 1D 1;(2)求证:EF ⊥B 1C ;(3)求三棱锥B 1-EFC 的体积.[解析] (1)证明:连结BD 1,在△DD 1B 中,E 、F 分别为D 1D ,DB 的中点,则EF ∥D 1B ,又EF ⊄平面ABC 1D 1,D 1B ⊂平面ABC 1D 1,∴EF ∥平面ABC 1D 1.(2)证明:∵B 1C ⊥AB ,B 1C ⊥BC 1,AB ∩BC 1=B ,∴B 1C ⊥平面ABC 1D 1,又BD 1⊂平面ABC 1D 1,∴B 1C ⊥BD 1,又EF ∥BD 1,∴EF ⊥B 1C .(3)解:∵CF ⊥BD ,CF ⊥BB 1,∴CF ⊥平面BDD 1B 1,即CF ⊥平面EFB 1,且CF =BF = 2∵EF =12BD 1=3,B 1F =BF 2+BB 12=(2)2+22=6,B 1E =B 1D 12+D 1E 2=12+(22)2=3,∴EF 2+B 1F 2=B 1E 2,即∠EFB 1=90°,∴VB 1-EFC =VC -B 1EF =13·S △B 1EF ·CF =13×12·EF ·B 1F ·CF =13×12×3×6×2=1. (理)(2010·河北唐山)如图,在四棱锥V -ABCD 中,底面ABCD 是矩形,侧棱VA ⊥底面ABCD ,E 、F 、G 分别为VA 、VB 、BC 的中点.(1)求证:平面EFG ∥平面VCD ;(2)当二面角V -BC -A 、V -DC -A 依次为45°、30°时,求直线VB 与平面EFG 所成的角.[解析] (1)∵E 、F 、G 分别为VA 、VB 、BC 的中点,∴EF ∥AB ,FG ∥VC ,又ABCD 是矩形,∴AB ∥CD ,∴EF ∥CD ,又∵EF ⊄平面VCD ,FG ⊄平面VCD ,∴EF ∥平面VCD ,FG ∥平面VCD ,又EF ∩FG =F ,∴平面EFG ∥平面VCD .(2)∵VA ⊥平面ABCD ,CD ⊥AD ,∴CD ⊥VD .则∠VDA 为二面角V -DC -A 的平面角,∴∠VDA =30°.同理∠VBA =45°.作AH ⊥VD ,垂足为H ,由上可知CD ⊥平面VAD ,则AH ⊥平面VCD .∵AB ∥平面VCD ,∴AH 即为B 到平面VCD 的距离.由(1)知,平面EFG ∥平面VCD ,则直线VB 与平面EFG 所成的角等于直线VB 与平面VCD 所成的角,记这个角为θ.∵AH =VA sin60°=32VA ,VB =2VA ,∴sin θ=AH VB =64, 故直线VB 与平面EFG 所成的角是arcsin64.。
高考数学复习—立体几何:(二)空间直线平面关系判断与证明—平行与垂直关系证明(试题版)
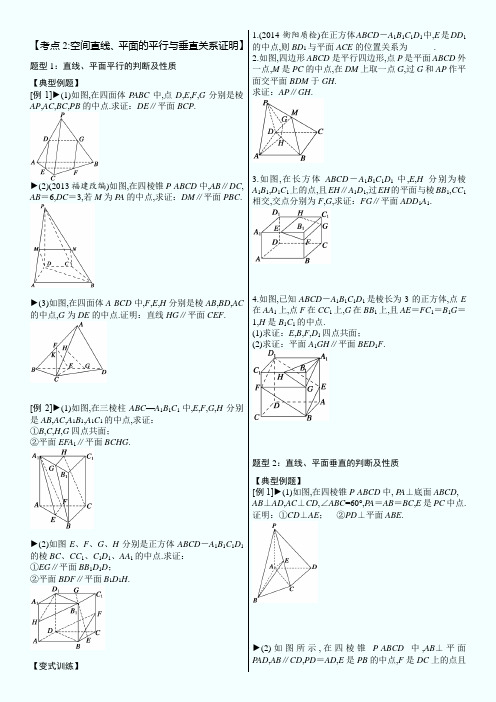
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。
立体几何大题15种题型全归纳

【题型一】 平行1:四边形法证线面平行【典例分析】如图,在正方体中,E ,F 分别是,CD 的中点.(1)求证:平面;(2)求异面直线与所成角的余弦值.【答案】(1)证明见解析;(2(1)在正方体中,取中点G ,连接FG ,,如图,而F 是CD 的中点,则,,又E 是的中点,则,, 因此,,,四边形是平行四边形,有,而平面,平面,平面.【经验总结】基本规律1.利用平移法做出平行四边形2.利用中位线做出平行四边形【变式演练】1.如图所示,在四棱锥P -ABCD 中,PC ⊥底面ABCD ,,,,E 是PB 的中点.(1)求证:平面PAD ;(2)若,求三棱锥P -ACE 的体积.【答案】(1)证明见解析(2) 【分析】(1)取PA 的中点F ,连接EF ,DF ,利用平行四边形证明,再由线面平行的判定定理即可得证;(2)根据等体积法知,即可由棱锥体积公式求解.(1)取PA 的中点F ,连接EF ,DF ,∵点E ,F 分别为PB ,PA 的中点,1111ABCD A B C D -1AA //EF 11A CD 1ED 1A C 1111ABCD A B C D -1CD 1GA 1//FG DD 112FG DD =1AA 11//A E DD 1112A E DD =1//A E FG 1A E FG =1FGA E 1//EF GA EF ⊄11A CD 1GA ⊂11A CD //EF 11A CD AB AD ⊥//AB CD 222AB AD CD ===//CE 2PC =13//EC DF P ACE E ACP V V --=∴,,∴四边形EFDC 是平行四边形,∴,又∵平面PAD ,平面PAD ,∴平面PAD ;2.如图,在四棱锥中,面,,且,,,,为的中点.(1)求证:平面;(2)求平面与平面所成二面角的余弦值;(3)在线段上是否存在一点,使得直线与平面若存在求出的值,若不存在说明理由. 【答案】(1)证明见解析(2)(3)存在, (1)证明:取CP 中点F ,连接NF 、BF ,因为F ,N 分为PC ,PD 的中点,则,且, 又,且,,所以四边形NABF 是平行四边形, ,又面PBC ,面PBC 。
立体几何高考常考题型

空间位置关系的判断与证明(1)高考对此部分的命题较为稳定,一般为“一小一大”或“一大”,即一道选择题(或填空题)和一道解答题或只考一道解答题.(2)选择题一般在第9~11题的位置,填空题一般在第14题的位置,多考查线面位置关系的判断,难度较小.(3)解答题多出现在第18或19题的第一问的位置,考查空间中平行或垂直关系的证明,难度中等.考点一 空间点、线、面的位置关系[大稳定——常规角度考双基]1.[命题真假的判定]已知直线m ,l ,平面α,β,且m ⊥α,l ⊂β,给出下列命题: ①若α∥β,则m ⊥l ;②若α⊥β,则m ∥l ;③若m ⊥l ,则α⊥β;④若m ∥l ,则α⊥β.其中正确的命题是( )A .①④B .③④C .①②D .①③解析:选A 对于①,若α∥β,m ⊥α,则m ⊥β,又l ⊂β,所以m ⊥l ,故①正确,排除B.对于④,若m ∥l ,m ⊥α,则l ⊥α,又l ⊂β,所以α⊥β.故④正确.故选A.2.[判断直线与直线的位置关系](2019·全国卷Ⅲ)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则( )A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线解析:选B 法一:取CD 的中点O ,连接EO ,ON .由△ECD 是正三角形,平面ECD ⊥平面ABCD ,知EO ⊥平面ABCD .∴EO ⊥CD ,EO ⊥ON .又N 为正方形ABCD 的中心,∴ON ⊥CD .以CD 的中点O 为原点, OD ―→方向为x 轴正方向建立空间直角坐标系,如图①所示.不妨设AD =2,则E (0,0,3),N (0,1,0),D (1,0,0),M ⎝⎛⎭⎫12,0,32,B (-1,2,0),∴EN = 12+(-3)2=2,BM = ⎝⎛⎭⎫322+4+34=7, ∴EN ≠BM .连接BD ,BE ,∵点N 是正方形ABCD 的中心,∴点N 在BD 上,且BN =DN ,∴BM ,EN 是△DBE 的中线,∴BM ,EN 必相交.故选B.法二:如图②,取CD 的中点F ,DF 的中点G ,连接EF ,FN ,MG ,GB .∵△ECD 是正三角形,∴EF ⊥CD .∵平面ECD ⊥平面ABCD ,∴EF ⊥平面ABCD .∴EF ⊥FN .不妨设AB =2,则FN =1,EF =3,∴EN = FN 2+EF 2=2.∵EM =MD ,DG =GF ,∴MG ∥EF 且MG =12EF ,∴MG ⊥平面ABCD , ∴MG ⊥BG .∵MG =12EF =32, BG = CG 2+BC 2= ⎝⎛⎭⎫322+22=52, ∴ BM = MG 2+BG 2=7.∴ BM ≠EN .连接BD ,BE ,∵ 点N 是正方形ABCD 的中心,∴ 点N 在BD 上,且BN =DN ,∴ BM ,EN 是△DBE 的中线,∴ BM ,EN 必相交.故选B.3.[线面垂直、面面垂直的判定]如图,在正方形ABCD 中,E ,F 分别是BC ,CD 的中点,G 是EF 的中点,现在沿AE ,AF 及EF 把这个正方形折成一个空间图形,使B ,C ,D 三点重合,重合后的点记为H ,那么,在这个空间图形中必有( )A .AG ⊥平面EFHB .AH ⊥平面EFHC .HF ⊥平面AEFD .HG ⊥平面AEF解析:选B 根据折叠前、后AH ⊥HE ,AH ⊥HF 不变,得AH ⊥平面EFH ,B 正确;∵过A 只有一条直线与平面EFH 垂直,∴A 不正确;∵AG ⊥EF ,EF ⊥GH ,AG ∩GH =G ,∴EF ⊥平面HAG ,又EF ⊂平面AEF ,∴平面HAG ⊥AEF ,过H 作直线垂直于平面AEF ,一定在平面HAG 内,∴C 不正确;由条件证不出HG ⊥平面AEF ,∴D 不正确.故选B.4.[求异面直线所成的角](2018·全国卷Ⅱ)在正方体ABCD A 1B 1C 1D 1中,E 为棱CC 1的中点,则异面直线AE 与CD 所成角的正切值为( )A .22B .32C .52D .72解析:选C 如图,连接BE ,因为AB ∥CD ,所以AE 与CD 所成的角为∠EAB .在Rt △ABE 中,设AB =2,则BE =5,则tan ∠EAB =BE AB =52,所以异面直线AE 与CD 所成角的正切值为52.故选C. [解题方略]判断与空间位置关系有关命题真假的3种方法(1)借助空间线面平行、面面平行、线面垂直、面面垂直的判定定理和性质定理进行判断;(2)借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理进行判断;(3)借助于反证法,当从正面入手较难时,可利用反证法,推出与题设或公认的结论相矛盾的命题,进而作出判断.[小创新——变换角度考迁移]1.[与充要条件交汇](2019·全国卷Ⅱ)设α,β为两个平面,则α∥β的充要条件是( )A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面解析:选B 若α∥β,则α内有无数条直线与β平行,反之不成立;若α,β平行于同一条直线,则α与β可以平行也可以相交;若α,β垂直于同一平面,则α与β可以平行也可以相交,故A 、C 、D 均不是充要条件.根据平面与平面平行的判定定理知,若一个平面内有两条相交直线与另一个平面平行,则两平面平行,反之成立.因此B 中条件是α∥β的充要条件.故选B.2.[与命题的交汇](2019·北京高考)已知l ,m 是平面α外的两条不同直线.给出下列三个论断:①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:____________.解析:已知l ,m 是平面α外的两条不同直线,由①l ⊥m 与②m ∥α,不能推出③l ⊥α,因为l 可以与α平行,也可以相交不垂直;由①l ⊥m 与③l ⊥α能推出②m ∥α;由②m ∥α与③l ⊥α可以推出①l ⊥m .故正确的命题是②③⇒①或①③⇒②.答案:②③⇒①或①③⇒②3.[线面角与其他问题的交汇](2018·全国卷Ⅱ)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°,若△SAB 的面积为515,则该圆锥的侧面积为________.解析:如图,∵SA 与底面成45°角,∴△SAO 为等腰直角三角形.设OA =r ,则SO =r ,SA =SB =2r .在△SAB 中,cos ∠ASB =78,∴sin ∠ASB =158, ∴S △SAB =12SA ·SB ·sin ∠ASB =12×(2r )2×158=515,解得r=210,∴SA=2r=45,即母线长l=45,∴S圆锥侧=πrl=π×210×45=402π.答案:402π考点二空间平行、垂直关系的证明[例1]如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点,求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.[证明](1)∵平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,PA⊂平面PAD,∴PA⊥底面ABCD.(2)∵AB∥CD,CD=2AB,E为CD的中点,∴AB∥DE,且AB=DE.∴四边形ABED为平行四边形.∴BE∥AD.又∵BE⊄平面PAD,AD⊂平面PAD,∴BE∥平面PAD.(3)∵AB⊥AD,且四边形ABED为平行四边形.∴BE⊥CD,AD⊥CD,由(1)知PA⊥底面ABCD.∴PA⊥CD.∵PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,∴CD⊥平面PAD,又PD⊂平面PAD,∴CD⊥PD.∵E和F分别是CD和PC的中点,∴PD∥EF,∴CD⊥EF.又BE⊥CD且EF∩BE=E,∴CD⊥平面BEF.又CD⊂平面PCD,∴平面BEF⊥平面PCD.[解题方略]1.直线、平面平行的判定及其性质(1)线面平行的判定定理:a⊄α,b⊂α,a∥b⇒a∥α.(2)线面平行的性质定理:a ∥α,a ⊂β,α∩β=b ⇒a ∥b .(3)面面平行的判定定理:a ⊂β,b ⊂β,a ∩b =P ,a ∥α,b ∥α⇒α∥β.(4)面面平行的性质定理:α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b .2.直线、平面垂直的判定及其性质(1)线面垂直的判定定理:m ⊂α,n ⊂α,m ∩n =P ,l ⊥m ,l ⊥n ⇒l ⊥α.(2)线面垂直的性质定理:a ⊥α,b ⊥α⇒a ∥b .(3)面面垂直的判定定理:a ⊂β,a ⊥α⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l ,a ⊂α,a ⊥l ⇒a ⊥β.[多练强化]1.如图,在四棱锥P -ABCD 中,平面PAB ⊥平面ABCD ,AD ∥BC ,PA ⊥AB ,CD ⊥AD ,BC =CD =12AD . 求证:(1)PA ⊥CD ;(2)平面PBD ⊥平面PAB .证明:(1)因为平面PAB ⊥平面ABCD ,平面PAB ∩平面ABCD =AB ,又因为PA ⊥AB ,所以PA ⊥平面ABCD ,又CD ⊂平面ABCD ,所以PA ⊥CD .(2)取AD 的中点为E ,连接BE ,由已知得,BC ∥ED ,且BC =ED ,所以四边形BCDE 是平行四边形,又CD ⊥AD ,BC =CD ,所以四边形BCDE 是正方形,连接CE ,所以BD ⊥CE .又因为BC ∥AE ,BC =AE ,所以四边形ABCE 是平行四边形,所以CE ∥AB ,则BD ⊥AB .由(1)知PA ⊥平面ABCD ,所以PA ⊥BD ,又因为PA ∩AB =A ,所以BD ⊥平面PAB ,因为BD ⊂平面PBD ,所以平面PBD ⊥平面PAB .2.如图,四边形ABCD 与四边形ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ;(2)平面BDE ∥平面MNG .证明:(1)如图,连接AE ,则AE 必过DF 与GN 的交点O ,连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO ,又BE ⊄平面DMF ,MO ⊂平面DMF ,所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN ,又DE ⊄平面MNG ,GN ⊂平面MNG ,所以DE ∥平面MNG .又M 为AB 的中点,N 为AD 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN ,又BD ⊄平面MNG ,MN ⊂平面MNG ,所以BD ∥平面MNG ,又DE 与BD 为平面BDE 内的两条相交直线,所以平面BDE ∥平面MNG .考点三 平面图形中的折叠问题[例2] 如图①,在直角梯形ABCD 中,∠ADC =90°,AB ∥CD ,AD =CD =12AB =2,E 为AC 的中点,将△ACD 沿AC 折起,使折起后的平面ACD 与平面ABC 垂直,如图②.在图②所示的几何体D ABC 中.(1)求证:BC ⊥平面ACD ;(2)点F 在棱CD 上,且满足AD ∥平面BEF ,求几何体F -BCE 的体积.[解] (1)证明:∵AC = AD 2+CD 2=22,∠BAC =∠ACD =45°,AB =4,∴在△ABC 中,BC 2=AC 2+AB 2-2AC ×AB ×cos 45°=8,∴AB 2=AC 2+BC 2=16,∴AC ⊥BC ,∵平面ACD ⊥平面ABC ,平面ACD ∩平面ABC =AC ,BC ⊂平面ABC ,∴BC ⊥平面ACD .(2)∵AD ∥平面BEF ,AD ⊂平面ACD ,平面ACD ∩平面BEF =EF ,∴AD ∥EF ,∵E 为AC 的中点,∴EF 为△ACD 的中位线,由(1)知,V F BCE =V B CEF =13×S △CEF ×BC , S △CEF =14S △ACD =14×12×2×2=12, ∴V F BCE =13×12×22=23. [解题方略] 平面图形折叠问题的求解方法(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量,一般情况下,线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.(2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形.[多练强化]如图①,在矩形ABCD 中,AB =3,BC =4,E ,F 分别在线段BC ,AD 上,EF ∥AB ,将矩形ABEF 沿EF 折起,记折起后的矩形为MNEF ,且平面MNEF ⊥平面ECDF ,如图②.(1)求证:NC ∥平面MFD ;(2)若EC =3,求证:ND ⊥FC ;(3)求四面体NEFD 体积的最大值.解:(1)证明:∵四边形MNEF 和四边形EFDC 都是矩形,∴MN ∥EF ,EF ∥CD ,MN =EF =CD ,∴MN 綊CD .∴四边形MNCD 是平行四边形,∴NC ∥MD .∵NC ⊄平面MFD ,MD ⊂平面MFD ,∴NC ∥平面MFD .(2)证明:连接ED ,∵平面MNEF ⊥平面ECDF ,且NE ⊥EF ,平面MNEF ∩平面ECDF =EF ,NE ⊂平面MNEF ,∴NE ⊥平面ECDF .∵FC ⊂平面ECDF ,∴FC ⊥NE .∵EC =CD ,∴四边形ECDF 为正方形,∴FC ⊥ED .又∵ED ∩NE =E ,ED ,NE ⊂平面NED ,∴FC ⊥平面NED .∵ND ⊂平面NED ,∴ND ⊥FC .(3)设NE =x ,则FD =EC =4-x ,其中0<x <4,由(2)得NE ⊥平面FEC ,∴四面体NEFD 的体积为V NEFD =13S △EFD ·NE =13×12×3×(4-x )x =12x (4-x ). ∴V 四面体NEFD ≤12⎣⎢⎡⎦⎥⎤x +(4-x )22=2,当且仅当x=4-x,即x=2时,四面体NEFD的体积最大,最大值为2.逻辑推理——转化思想在平行、垂直证明中的应用[典例]如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.[证明](1)在平面ABD内,因为AB⊥AD,EF⊥AD,所以EF∥AB,又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC.又因为AC⊂平面ABC,所以AD⊥AC.[素养通路]本题(1)证明线面平行的思路是转化为证明线线平行,即证明EF与平面ABC内的一条直线平行,从而得到EF∥平面ABC;(2)证明线线垂直可转化为证明线面垂直,由平面ABD⊥平面BCD,根据面面垂直的性质定理得BC⊥平面ABD,则可证明AD⊥平面ABC,再根据线面垂直的性质,得到AD⊥AC.考查了逻辑推理这一核心素养.[专题过关检测]A组——“6+3+3”考点落实练一、选择题1.设α为平面,a,b为两条不同的直线,则下列叙述正确的是()A.若a∥α,b∥α,则a∥bB.若a⊥α,a∥b,则b⊥αC.若a⊥α,a⊥b,则b∥αD.若a∥α,a⊥b,则b⊥α解析:选B若a∥α,b∥α,则a与b相交、平行或异面,故A错误;易知B正确;若a⊥α,a⊥b,则b∥α或b⊂α,故C错误;若a∥α,a⊥b,则b∥α或b⊂α或b与α相交,故D错误.故选B.2.设l是直线,α,β是两个不同的平面,则下列说法正确的是()A.若l∥α,l∥β,则α∥βB.若l∥α,l⊥β,则α⊥βC.若α⊥β,l⊥α,则l∥βD.若α⊥β,l∥α,则l⊥β解析:选B对于A,若l∥α,l∥β,则α∥β或α与β相交,故A错误;易知B正确;对于C,若α⊥β,l⊥α,则l∥β或l⊂β,故C错误;对于D,若α⊥β,l∥α,则l与β的位置关系不确定,故D错误.故选B.3.如图,在三棱锥D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的是()A.平面ABC⊥平面ABDB.平面ABD⊥平面BCDC.平面ABC⊥平面BDE,且平面ACD⊥平面BDED.平面ABC⊥平面ACD,且平面ACD⊥平面BDE解析:选C因为AB=CB,且E是AC的中点,所以BE⊥AC,同理,DE⊥AC,由于DE∩BE=E,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE.故选C.4.已知m,n是两条不同的直线,α,β是两个不同的平面,给出四个命题:①若α∩β=m,n⊂α,n⊥m,则α⊥β;②若m⊥α,m⊥β,则α∥β;③若m⊥α,n⊥β,m⊥n,则α⊥β;④若m∥α,n∥β,m∥n,则α∥β.其中正确的命题是()A.①②B.②③C .①④D .②④解析:选B 两个平面斜交时也会出现一个平面内的直线垂直于两个平面的交线的情况,①不正确;垂直于同一条直线的两个平面平行,②正确;当两个平面与两条互相垂直的直线分别垂直时,它们所成的二面角为直二面角,故③正确;当两个平面相交时,分别与两个平面平行的直线也平行,故④不正确.故选B.5.在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22解析:选C 如图,连接BD 1,交DB 1于O ,取AB 的中点M ,连接DM ,OM ,易知O 为BD 1的中点,所以AD 1∥OM ,则∠MOD 为异面直线AD 1与DB 1所成角.因为在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,AD 1=AD 2+DD 21=2,DM =AD 2+⎝⎛⎭⎫12AB 2=52,DB 1=AB 2+AD 2+DD 21=5,所以OM =12AD 1=1,OD =12DB 1=52,于是在△DMO 中,由余弦定理,得cos ∠MOD =12+⎝⎛⎭⎫522-⎝⎛⎭⎫5222×1×52=55,即异面直线AD 1与DB 1所成角的余弦值为55.故选C. 6.如图,在矩形ABCD 中,AB =3,BC =1,将△ACD 沿AC 折起,使得D 折起后的位置为D 1,且D 1在平面ABC 上的射影恰好落在AB 上,在四面体D 1ABC 的四个面中,有n 对平面相互垂直,则n 等于( )A .2B .3C .4D .5解析:选B 如图,设D 1在平面ABC 上的射影为E ,连接D 1E ,则D 1E ⊥平面ABC ,因为D 1E ⊂平面ABD 1,所以平面ABD 1⊥平面ABC .因为D 1E ⊥平面ABC ,BC ⊂平面ABC , 所以D 1E ⊥BC ,又AB ⊥BC ,D 1E ∩AB =E , 所以BC ⊥平面ABD 1, 又BC ⊂平面BCD 1,所以平面BCD 1⊥平面ABD 1,因为BC ⊥平面ABD 1,AD 1⊂平面ABD 1, 所以BC ⊥AD 1,又CD 1⊥AD 1,BC ∩CD 1=C , 所以AD 1⊥平面BCD 1,又AD 1⊂平面ACD 1, 所以平面ACD 1⊥平面BCD 1. 所以共有3对平面互相垂直.故选B. 二、填空题7.正方体ABCD -A 1B 1C 1D 1的棱长为2,点M 为CC 1的中点,点N 为线段DD 1上靠近D 1的三等分点,平面BMN 交AA 1于点Q ,则线段AQ 的长为________.解析:如图所示,在线段DD 1上靠近点D 处取一点T ,使得DT =13,因为N 是线段DD 1上靠近D 1的三等分点,故D 1N =23,故NT =2-13-23=1,因为M 为CC 1的中点,故CM =1,连接TC ,由NT ∥CM ,且CM =NT =1,知四边形CMNT 为平行四边形,故CT ∥MN ,同理在AA 1上靠近A 处取一点Q ′,使得AQ ′=13,连接BQ ′,TQ ′,则有BQ ′∥CT ∥MN ,故BQ ′与MN 共面,即Q ′与Q 重合,故AQ =13.答案:138.如图,∠ACB =90°,DA ⊥平面ABC ,AE ⊥DB 交DB 于点E ,AF ⊥DC 交DC 于点F ,且AD =AB =2,则三棱锥D -AEF 体积的最大值为________.解析:因为DA ⊥平面ABC ,所以DA ⊥BC ,又BC ⊥AC ,DA ∩AC=A ,所以BC ⊥平面ADC ,所以BC ⊥AF .又AF ⊥CD ,BC ∩CD =C ,所以AF ⊥平面DCB ,所以AF ⊥EF ,AF ⊥DB .又DB ⊥AE ,AE ∩AF =A ,所以DB ⊥平面AEF ,所以DE 为三棱锥D -AEF 的高.因为AE 为等腰直角三角形ABD 斜边上的高,所以AE =2,设AF =a ,FE =b ,则△AEF 的面积S =12ab ≤12·a 2+b 22=12×22=12,所以三棱锥D -AEF 的体积V ≤13×12×2=26(当且仅当a =b =1时等号成立).答案:269.在长方体ABCD -A 1B 1C 1D 1中,AB =AD =4,AA 1=2.过点A 1作平面α与AB ,AD 分别交于M ,N 两点,若AA 1与平面α所成的角为45°,则截面A 1MN 面积的最小值是________.解析:如图,过点A 作AE ⊥MN ,连接A 1E ,因为A 1A ⊥平面ABCD ,所以A 1A ⊥MN ,所以MN ⊥平面A 1AE ,所以A 1E ⊥MN ,平面A 1AE ⊥平面A 1MN ,所以∠AA 1E 为AA 1与平面A 1MN 所成的角,所以∠AA 1E =45°,在Rt △A 1AE 中,因为AA 1=2,所以AE =2,A 1E =22,在Rt △MAN 中,由射影定理得ME ·EN =AE 2=4,由基本不等式得MN =ME +EN ≥2ME ·EN =4,当且仅当ME =EN ,即E 为MN 的中点时等号成立,所以截面A 1MN 面积的最小值为12×4×22=4 2.答案:4 2 三、解答题10.(2019·全国卷Ⅲ)图①是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图②.(1)证明:图②中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图②中的四边形ACGD 的面积.解:(1)证明:由已知得AD ∥BE ,CG ∥BE ,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°,得EM⊥CG,故CG⊥平面DEM.因此DM⊥CG.在Rt△DEM中,DE=1,EM=3,故DM=2.所以四边形ACGD的面积为4.11.如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.求证:(1)AF∥平面BCE;(2)平面BCE⊥平面CDE.证明:(1)如图,取CE的中点G,连接FG,BG.因为F为CD的中点,所以GF∥DE且GF=12DE.因为AB⊥平面ACD,DE⊥平面ACD,所以AB∥DE,所以GF∥AB.又因为AB=12DE,所以GF=AB.所以四边形GFAB为平行四边形,则AF∥BG.因为AF⊄平面BCE,BG⊂平面BCE,所以AF∥平面BCE.(2)因为△ACD为等边三角形,F为CD的中点,所以AF⊥CD.因为DE⊥平面ACD,AF⊂平面ACD,所以DE⊥AF.又CD∩DE=D,所以AF⊥平面CDE.因为BG∥AF,所以BG⊥平面CDE.又因为BG⊂平面BCE,所以平面BCE⊥平面CDE.12.如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.(1)求证:AB⊥平面ADC;(2)若AD=1,AC与其在平面ABD内的正投影所成角的正切值为6,求点B到平面ADE的距离.解:(1)证明:因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,又DC⊥BD,DC⊂平面BCD,所以DC⊥平面ABD.因为AB⊂平面ABD,所以DC⊥AB.又因为折叠前后均有AD⊥AB,且DC∩AD=D,所以AB⊥平面ADC.(2)由(1)知DC⊥平面ABD,所以AC在平面ABD内的正投影为AD,即∠CAD为AC与其在平面ABD内的正投影所成的角.=6,依题意知tan∠CAD=DCAD因为AD=1,所以DC= 6.设AB =x (x >0),则BD = x 2+1, 易知△ABD ∽△DCB ,所以AB AD =DC BD, 即x 1=6x 2+1,解得x =2,故AB =2,BD =3,BC =3. 由于AB ⊥平面ADC ,所以AB ⊥AC ,又E 为BC 的中点,所以由平面几何知识得AE =BC 2=32,同理DE =BC 2=32,∴S △ADE =12×1×⎝⎛⎭⎫322-⎝⎛⎭⎫122=22,∵DC ⊥平面ABD∴V A BCD =13CD ·S △ABD =33,设点B 到平面ADE 的距离为d ,则13d ·S △ADE =V B ADE =V A BDE =12V A BCD =36, ∴d =62,即点B 到平面ADE 的距离为62. B 组——大题专攻强化练1.如图,三棱柱ABC -A 1B 1C 1中,底面ABC 是等边三角形,侧面BCC 1B 1是矩形,AB =A 1B ,N 是B 1C 的中点,M 是棱AA 1上的点,且AA 1⊥CM .(1)证明:MN ∥平面ABC ;(2)若AB ⊥A 1B ,求二面角A -CM -N 的余弦值.解:(1)证明:如图1,在三棱柱ABC -A 1B 1C 1中,连接BM .因为BCC 1B 1是矩形,所以BC ⊥BB 1.因为AA 1∥BB 1,所以AA 1⊥BC . 又AA 1⊥MC ,BC ∩MC =C ,所以AA 1⊥平面BCM , 所以AA 1⊥MB ,又AB =A 1B ,所以M 是AA 1的中点.取BC 的中点P ,连接NP ,AP ,因为N 是B 1C 的中点,所以NP ∥BB 1,且NP =12BB 1,所以NP ∥MA ,且NP =MA ,所以四边形AMNP 是平行四边形,所以MN ∥AP . 又MN ⊄平面ABC ,AP ⊂平面ABC ,所以MN ∥平面ABC .(2)因为AB ⊥A 1B ,所以△ABA 1是等腰直角三角形,设AB =2a , 则AA 1=2a ,BM =AM =a .又在Rt △ACM 中,AC =2a ,所以MC =a . 在△BCM 中,CM 2+BM 2=2a 2=BC 2,所以MC ⊥BM ,所以MA 1,MB ,MC 两两垂直,如图2,以M 为坐标原点, MA 1―→,MB ―→,MC ―→的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则M (0,0,0),C (0,0,a ),B 1(2a ,a ,0),所以MC ―→=(0,0,a ),N ⎝⎛⎭⎫a ,a 2,a 2,则MN ―→=⎝⎛⎭⎫a ,a 2,a 2. 设平面CMN 的法向量为n 1=(x ,y ,z ),则⎩⎪⎨⎪⎧n 1·MC ―→=0,n 1·MN ―→=0,即⎩⎪⎨⎪⎧az =0,ax +a 2y +a 2z =0,得z =0, 取x =1得y =-2.故平面CMN 的一个法向量为n 1=(1,-2,0). 因为平面ACM 的一个法向量为n 2=(0,1,0), 所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-255.因为二面角A -CM -N 为钝角, 所以二面角A -CM -N 的余弦值为-255.2.如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,底面ABCD 为菱形,E为CD的中点.(1)求证:BD⊥平面PAC;(2)若∠ABC=60°,求证:平面PAB⊥平面PAE;(3)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.解:(1)证明:因为PA⊥平面ABCD,所以PA⊥BD.因为底面ABCD为菱形,所以BD⊥AC.又PA∩AC=A,所以BD⊥平面PAC.(2)证明:因为PA⊥平面ABCD,AE⊂平面ABCD,所以PA⊥AE.因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.所以AB⊥AE.又AB∩PA=A,所以AE⊥平面PAB.因为AE⊂平面PAE,所以平面PAB⊥平面PAE.(3)棱PB上存在点F,使得CF∥平面PAE.取PB的中点F,PA的中点G,连接CF,FG,EG,则FG∥AB,且FG=12AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.因为CF⊄平面PAE,EG⊂平面PAE,所以CF∥平面PAE.3.如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点,将△ABE 沿BE 折起到图2中△A 1BE 的位置,得到四棱锥A 1BCDE .(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值. 解:(1)证明:在图1中,因为AB =BC =12AD =a ,E 是AD 的中点,∠BAD =π2,所以BE ⊥AC .即在图2中,BE ⊥A 1O ,BE ⊥OC , 从而BE ⊥平面A 1OC , 又CD ∥BE , 所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE , 且平面A 1BE ∩平面BCDE =BE , 又由(1)知,A 1O ⊥BE , 所以A 1O ⊥平面BCDE , 即A 1O 是四棱锥A 1BCDE 的高. 由图1知,A 1O =22AB =22a ,平行四边形BCDE 的面积S =BE ·OC =a 2. 从而四棱锥A 1BCDE 的体积为 V =13×S ×A 1O =13×a 2×22a =26a 3,由26a 3=362,得a =6. 4.(2019·天津高考)如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,△PCD 为等边三角形,平面PAC ⊥平面PCD ,PA⊥CD ,CD =2,AD =3.(1)设G ,H 分别为PB ,AC 的中点,求证:GH ∥平面PAD ;(2)求证:PA ⊥平面PCD ;(3)求直线AD 与平面PAC 所成角的正弦值.解:(1)证明:连接BD ,易知AC ∩BD =H ,BH =DH .又由BG =PG ,故GH ∥PD .又因为GH ⊄平面PAD ,PD ⊂平面PAD ,所以GH ∥平面PAD .(2)证明:取棱PC 的中点N ,连接DN .依题意,得DN ⊥PC .又因为平面PAC ⊥平面PCD ,平面PAC ∩平面PCD =PC ,所以DN ⊥平面PAC .又PA ⊂平面PAC ,所以DN ⊥PA .又已知PA ⊥CD ,CD ∩DN =D ,所以PA ⊥平面PCD .(3)连接AN ,由(2)中DN ⊥平面PAC ,可知∠DAN 为直线AD 与平面PAC 所成的角. 因为△PCD 为等边三角形,CD =2且N 为PC 的中点,所以DN = 3.又DN ⊥AN ,在Rt △AND 中,sin ∠DAN =DN AD =33. 所以,直线AD 与平面PAC 所成角的正弦值为33.。
高考数学立体几何题型大全总结

高考数学立体几何题型大全总结1. 三角锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
2. 三棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
3. 四棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
4. 圆锥的体积公式
体积公式:V=1/3∗π∗r2∗h
其中,r为圆锥的半径,h为圆锥的高。
5. 球的体积公式
体积公式:V=4/3∗π∗r3
其中,r为球的半径。
6. 圆柱的体积公式
体积公式:V=π∗r2∗h
其中,r为圆柱的半径,h为圆柱的高。
7. 圆台的体积公式
体积公式:V=1/3∗π∗h∗(r12+r22+r1r2)
其中,r1,r2为底面半径,h为圆台高。
8. 空间向量的共线与垂直判定公式
共线判定公式:
如果两个向量a,b共线,则有a=kb,其中k为一个实数。
垂直判定公式:
如果两个向量a,b垂直,则有a·b=0,其中“·”表示向量的数量积。
9. 空间向量的平面垂直判定公式
若向量a与平面P垂直,则a在平面P上的投影为零向量。
10. 空间向量的平面共面判定公式
若向量a和向量b在同一平面上,则a和b的向量积c在该平面内。
11. 空间中两直线相交的条件
两直线相交的条件是它们至少有一个公共点,并且既不平行也不重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考《立体几何》判断命题题型
2008年高考
1.(某某文理).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是()
A .,,αγβγαβ⊥⊥若则‖
B .,,m n m n αα⊥⊥若则‖
C .,,m n m n αα若则‖‖‖
D .,,m m αβαβ若则‖‖‖
2.(某某文)已知平面α⊥平面β,l αβ=,点A α∈,A l ∉,直线AB l ∥,直线AC l ⊥,
直线m m αβ∥,∥,则下列四种位置关系中,不一定成立的是()
A .A
B m ∥ B .A
C m ⊥C .AB β∥
D .AC β⊥
3.(某某文)已知直线m,n 和平面βα,满足βα⊥⊥⊥,,a m n m ,则 ( )
.A n β⊥,//.βn B 或β⊂n α⊥n C .,//.αn D 或α⊂n
4(某某理)设有直线m 、n 和平面α、β.下列四个命题中,正确的是( )
A.若m ∥α,n ∥α,则m ∥n
B.若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β
C.若α⊥β,m ⊂α,则m ⊥β
D.若α⊥β,m ⊥β,m ⊄α,则m ∥α
5.(某某文).设直线m 与平面α相交但不垂直,则下列说法中正确的是()
A .在平面α内有且只有一条直线与直线m 垂直
B .过直线m 有且只有一个平面与平面α垂直
C .与直线m 垂直的直线不可能与平面α平行
D .与直线m 平行的平面不可能与平面α垂直
6.(某某文理)给定空间中的直线l 及平面α.条件“直线l 与平面α内两条相交直线都垂直”是
“直线l 与平面α垂直”的( )
A.充分非必要条件 B.必要非充分条件 C .充要条件 D.既非充分又非必要条件
7.(某某文理) 设a b ,是两条直线,αβ,是两个平面,则a b ⊥的一个充分条件是()
A .a b αβαβ⊥⊥,∥,
B .a b αβαβ⊥⊥,,∥
C .a b αβαβ⊂⊥,,∥
D .a b αβαβ⊂⊥,∥,
8. (某某9)对两条不相交的空间直线a 和b ,必定存在平面α,使得 ( )
A .,a b αα⊂⊂
B .,//a b αα⊂
C .,a b αα⊥⊥
D .,a b αα⊂⊥
2007年高考
1.()平面α∥平面β的一个充分条件是( )
A .存在一条直线a a ααβ,∥,∥
B .存在一条直线a a a αβ⊂,,∥
C .存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥
D .存在两条异面直线a b a a b αβα⊂,,,∥,∥
2.(某某)设l ,m ,n 均为直线,其中m ,n 在平面α内,“l α⊥”是l m ⊥且“l n ⊥”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
3.(某某)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是()
A .,,//,////m n m n ααββαβ⊂⊂⇒
B .,//m m n n αα⊥⊥⇒
C .//,,//m n m n αβαβ⊂⊂⇒
D .//,m n n m αα⊥⇒⊥
4.(某某)平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是
1m 和1n ,给出下列四个命题:①
1m ⊥1n ⇒m ⊥n ;②m ⊥n ⇒1m ⊥1n ; ③1m 与1n 相交⇒m 与n 相交或重合;④1m 与1n 平行⇒m 与n 平行或重合;
其中不正确的命题个数是()
A.1
B.2
C.3
D.4
5.(某某)已知两条直线,m n ,两个平面,αβ,给出下面四个命题:
①//,m n m n αα⊥⇒⊥②//,,//m n m n αβαβ⊂⊂⇒
③//,////m n m n αα⇒④//,//,m n m n αβαβ⊥⇒⊥
其中正确命题的序号是()
A .①③
B .②④
C .①④
D .②③
6.(某某)若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题是()
A .若m βαβ⊂⊥,,则m α⊥
B .若m αγ=n βγ=,m n ∥,则αβ∥
C .若m β⊥,m α∥,则αβ⊥
D .若αγ⊥,αβ⊥,则βγ⊥
7.(某某)设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是() A.若a b ,与α所成的角相等,则a b ∥B.若a b αβ,∥∥,αβ∥,则a b ∥ C.若a b a b αβ⊂⊂,,∥,则αβ∥D.若a b αβ⊥⊥,,αβ⊥,则a b ⊥
8.(某某)若P 是两条异面直线,l m 外的任意一点,则()
A .过点P 有且仅有一条直线与,l m 都平行
B .过点P 有且仅有一条直线与,l m 都垂直
C .过点P 有且仅有一条直线与,l m 都相交
D .过点P 有且仅有一条直线与,l m 都异面 2006年高考
1.若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 A.充分非必要条件 B.必要非充分条件 C .充要条件 D.既非充分又非必要条件
2.设A 、B 、C 、D 是空间四个不同的点,在下列命题中,不正确的是()
(A )若AC 与BD 共面,则AD 与BC 共面
(B )若AC 与BD 是异面直线,则AD 与BC 是异面直线
(C) 若AB =AC ,DB =DC ,则AD =BC
(D) 若AB =AC ,DB =DC ,则AD ⊥BC
3. 对于任意的直线l 与平同a ,在平面a 内必有直线m ,使m 与l ()
(A)平行 (B )相交 (C)垂直 (D)互为异面直线
4.m 、n 是空间两条不同直线,αβ、是空间两条不同平面,下面有四个命题:
①,;m n m n αβαβ⊥⇒⊥, ②,,;m n m n αβαβ⊥⊥⇒
③,,;m n m n αβαβ⊥⇒⊥ ④,,;m m n n ααββ⊥⇒⊥ 其中真命题的编号是________(写出所有真命题的编号)。
5.若l 为一条直线,αβγ,,为三个互不重合的平面,给出下面三个命题:
①αγβγαβ⊥⊥⇒⊥,;②αγβγαβ⊥⇒⊥,∥;③l l αβαβ⊥⇒⊥,∥.
其中正确的命题有( )
A.0个B.1个C.2个D.3个
6. 关于直线m 、n 与平面α与β,有下列四个命题:
①若//,//m n αβ且//αβ,则//m n ;②若,m n αβ⊥⊥且αβ⊥,则m n ⊥; ③若,//m n αβ⊥且//αβ,则m n ⊥;④若//,m n αβ⊥且αβ⊥,则//m n ; 其中真命题的序号是
A .①②
B .③④
C .①④
D .②③ 7. 对于平面α和共面的直线m 、,n 下列命题中真命题是
A .若,,m m n α⊥⊥则n α∥
B .若m αα∥,n ∥,则m ∥n
C .若,m n αα⊂∥,则m ∥n
D .若m 、n 与α所成的角相等,则m ∥n
8. 给出下列四个命题:
①垂直于同一直线的两条直线互相平行; ②垂直于同一平面的两个平面互相平行.
③若直线
12,l l 与同一平面所成的角相等,则12,l l 互相平行. ④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线.
其中假命题的个数是: (A)1 (B)2 (C)3 (D)4
9.已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是( )
A.平面ABC 必平行于α
B.平面ABC 必与α相交
C.平面ABC 必不垂直于α
D.存在△ABC 的一条中位线平行于α或在α内
10. 给出以下四个命题:
○1如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
○2如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
○3如果两条直线都平行于一个平面,那么这两条直线互相平行。
○4如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
其中真命题的个数是( )
A.4
B.3
C.2
D.1。
