冀教版八年级上第17章《特殊三角形》单元测试(含答案解析)
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )A.3B.5C.3或5D.3或62、在平面直角坐标系中,已知点P(﹣2,﹣1)、A(﹣1,﹣3),点A关于点P的对称点为B,在坐标轴上找一点C,使得△ABC为直角三角形,这样的点C共有()个.A.5B.6C.7D.83、已知等腰三角形的周长为13,一条边长为5,则底边长为().A.3B.5C.5或3D.4或54、下列各组数中,能成为直角三角形的三条边长的是( )A.3,5,7B.5,7,8C.1,,2D.4,6,75、已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A.25海里B.30海里C.35海里D.40海里6、把一副三角板按如图放置,其中,,,斜边,若将三角板DEB绕点B逆时针旋转得到,则点A在的().A.内部B.外部C.边上D.以上都有可能7、如图,在△ABC中,AB=AC,∠B=40°,D为BC上一点,且AB=BD,则∠DAC的度数为()A.20°B.30°C.40°D.50°8、如图,在△ABC中,AB=AC,点E在BC边上,在线段AC的延长线上取点D,使得CD=CE,连接DE,CF是△CDE的中线,若∠FCE=52°,则∠A的度数为( )A.38°B.34°C.32°D.28°9、如图所示,BD平分∠ABC,DE∥BC,且∠D=30°,则∠AED的度数为()A.50°B.60°C.70°D.80°10、如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为()A.50B.50C.50 -50D.50 +5011、在半径为2R的圆中,垂直平分半径的弦长等于().A. B. C. D. R12、如图,矩形ABCD中,AB=14,AD=8,点E是CD的中点,DG平分∠ADC交AB于点G,过点A作AF⊥DG于点F,连接EF,则EF的长为()A.3B.4C.5D.613、小明从一根长6m的钢条上截取一段后,截取的钢条恰好与两根长分别为3m、5m的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为()A.4mB. mC.4m或mD.6m14、若一条长为31cm细线能围成一边长等于7cm的等腰三角形,该等腰三角形的腰长为()A.7cmB.9cmC.12cmD.7cm或12cm15、我国汉代数学家赵爽为了证明勾股定理,创制了一幅弦图,后人称其为赵爽弦图(如图1).,图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中,以点 B 为圆心,AB 为半径作 AC,再以CD 为直径作半圆交 AC 于点E,若边长AB=10,则△CDE 的面积为()A.20B.C.24D.二、填空题(共10题,共计30分)16、如图,在中,,为的角平分线,且于D,若,则的长为________.17、在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________ cm2.18、在△ABC中,∠A:∠B:∠C=1:2:3,AB=6cm,则AC=________cm19、如图所示,在△ABC中,∠B=90°,AB=3,AC=5,线段AC的垂直平分线DE交AC于D 交BC于E,则△ABE的周长为________.20、如图,点E在正方形ABCD的边CD上.若△ABE的面积为8,CE=3,则线段BE的长为________21、等腰三角形的腰长为17,底长为16,则其底边上的高为________.22、已知△ABC中,∠ACB=90°,,,为△ABC的重心,那么________.23、在Rt△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,a∶b=2∶3,c= ,则a=________.24、如图,OA=OB,点C在数轴上表示的数为2,且有BC垂直于数轴,若BC=1,则数轴上点A表示的数是________。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、△ABC的三条边分别为a,b,c,下列条件不能判断△ABC是直角三角形的是()A.a 2+b 2=c 2B.a=5,b=12,c=13C.∠A=∠B+∠CD.∠A:∠B:∠C=3:4:52、如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有 )A.0个B.1个C.2个D.3个3、在中,∠ACB=90°,斜边的中垂线分别交BC,AB于点D,E.已知BD=5,CD=3,则AC的长为( )A.8B.4C.D.24、如图,将一个等腰直角三角形按图中方式依次翻折,若DE=a,DC=b,则下列说法:①DC′平分∠BDE;②BC的长为2a+b;③△BC′D是等腰三角形;④△CED的周长等于BC的长.其中正确的是()A.①②③B.②④C.②③④D.③④5、如果三角形的某一边的中点到其他两边的距离相等,则这个三角形一定是()A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形6、在下列命题中正确的命题有()①面积相等的三角形全等;②有两边及第三边上的高线对应相等的两个三角形全等;③等腰三角形两腰上的中线相等;④直角三角形三边为,则A. B. C. D.7、如图,在△ABC 中 AB=AC,D、E 两点分别在 AC、BC 上,BD 是∠ABC 的平分线,DE∥AB,若 BE=5cm,CE=3cm,则△CDE 的周长是()A.13cmB.11cmC.9cmD.8cm8、若一个等腰三角形的腰长为5,底边长为6,则底边上的高为()A.4B.3C.5D.69、如图,斜面AC的坡比CD:AD=1:2.AC=3 m,坡有一旗杆BC.旗杆顶端B点与A点有一条绝缘钢端相连,若AB=10m.则旗杆BC的高度()A.5mB.6mC.8mD.(3+ )m10、如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )A.AB=ADB.CA平分∠BCDC.AB=BDD.△BEC≌△DEC2、如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD 上的一个动点,则PM+PN的最小值是()A. B.3 C. D.53、⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O 的位置关系是( )A.点P在⊙O内;B.点P的⊙O上C.点P在⊙O外;D.点P 在⊙O上或⊙O外4、等腰三角形的两边长分别为4和8,则这个等腰三角形的周长为()A.16B.20C.16或20D.185、若等腰三角形的周长为30cm,一边长为16cm,则腰长为()A.16cmB.7cmC.16cm或7cmD.以上都不对6、如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D 处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为()A. B. C. D.7、一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?()A.4米B.4.5米C.5米D.6米8、等腰三角形的一个角是50°,它的底角的度数是()A.65°B.50°C.65°或50°D.不能确定9、如图,将曲线c1:y=(x>0)绕原点O逆时针旋转60°得到曲线c2, A为直线y =x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6 ,直线y=x交曲线c1于点B,则OB的长()A.2B.5C.3D.10、如图,在中,其周长为20,⊙I是的内切圆,其半径为,则的外接圆半径为()A.7B.C.D.11、如图,在△ABC中,AB=AC,BD=BC,AD=DE=EB,则∠A是( )A.30°B.45°C.60°D.20°12、如图,在△ABC中,∠C=90°,∠B=30°,CD=1,AD平分∠CAB,交CB于点D,DE垂直平分AB,垂足为E,则AE的长是( )A.1B.C.2D.13、若等腰三角形的两边长分别是4和9,则它的周长是()A.17B.22C.17或22D.1314、如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、等腰三角形的底角为40º,则这个等腰三角形的顶角为()A.40 ºB.80 ºC.100 ºD.100 º或40 º2、已知在中,弦AB的长为8,圆心O到AB的距离为3,则的面积是()A. B. C. D.3、如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为()A.20B.12C.14D.134、“勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在中,,分别以的三条边为边向外作正方形,连结,,,分别与,相交于点P,Q.若,则的值为()A. B. C. D.5、已知等腰三角形的两边长分别是3和5,则该三角形的周长是()A.8B.9C.10或12D.11或136、木工师傅想利用木条制作一个直角三角形的工具,那么下列各组数据不符合直角三角形的三边长的是().A.3,4,5B.6,8,10C.5,12,13D.13,16,187、如图,在中,已知,点D,E分别在AC,AB上,且,,那么的度数是A. B. C. D.8、若△ABC的三边长分别为a、b、c,且满足(a-b)(a2+b2-c2)=0,则△ABC是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形9、如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有()A.①②③B.①②③④C.①②D.①10、把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为()A.7+3B.7+4C.8+3D.8+411、如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为()A.1.5B.2C. +D.12、如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,使得点P在坐标轴上.则这样的P点有()A.4个B.5个C.6个D.7个13、如图,在平面直角坐标系中,∠α的一边与轴正半轴重合,顶点为坐标原点,另一边过点,那么sinα的值为()A. B. C. D.14、如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F 两点,若AB=2EF,则k的值是()A.﹣1B.1C.D.15、以下四组数中,不是勾股数的是()A.8,5,7B.5,12,13C.20,21,29D.3n,4n,5n(n为正整数)二、填空题(共10题,共计30分)16、如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=________.17、如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=________度.18、等腰三角形的底角是15°,腰长为10,则其腰上的高为 ________ .19、如图,在△ABC中,∠B=30°,∠C=∠B,AB=2 cm,点P从点B开始以1cm/s的速度向点C移动,当△ABP要以AB为腰的等腰三角形时,则运动的时间为 ________.20、如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8,点E是AB的中点,以AE为边作等边△ADE(点D与点C分别在AB异侧),连接CD,则△ACD的面积是________.21、如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形中,,,则的长为________22、如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为________.23、如图,在△ABC中,∠C=90°,AC=BC=2 ,D是AB的中点,点E、F分别在AC、BC 边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF的周长不变;③点C到线段EF的最大距离为1.其中正确的结论有________.(填写所有正确结论的序号)24、如图,AB为⊙O的直径,CD为⊙O的弦,CD与AB交于点E,且EC=ED=8,AB=20,则AE=________.25、已知菱形的周长为,两条对角线的和为6,则菱形的面积为________三、解答题(共5题,共计25分)26、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.求AB的长.27、如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD2+CD2=2AD2 .28、用24cm长的绳子围成一边长为10cm的等腰三角形,求底边长.29、如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?30、如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.(1)求证:EF=AC.(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.参考答案一、单选题(共15题,共计45分)1、C2、C3、C4、D5、D6、D7、B8、D9、A10、D11、A12、D13、A15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、如图,在三角形纸片ABC中,,,折叠三角形纸片,使点A在BC边上的点E处,则AD是A.3B.4C.D.2、如图是用直尺和一个等腰直角三角尺画平行线的示意图,图中∠a的度数为()A.45°B.60°C.90°D.135°3、如图,在中,,点、在上,连接、,如果只添加一个条件使,则添加的条件不能为()A. B. C. D.4、将一副三角板按图1所示的方式放置,则∠AOB=()图1A.30°B.45°C.75°D.80°5、如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是()A.1个B.2个C.3个D.4个6、如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论:①DG=DF;②四边形EFDG是菱形;③EG2=GF×AF;④当AG=6,EG=2 时,BE的长为,其中正确的编号组合是()A.①②③B.①②④C.①③④D.①②③④7、如图,△ABC是半径为1的⊙O的内接正三角形,则圆的内接矩形BCDE的面积为()A.3B.C.D.8、如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是()A.①②③B.①②④C.②③④D.①③④9、如图,在中,已知,,平分交边于点E,则边的长等于()A.4cmB.6cmC.8cmD.12cm10、如图,在行距、列距都是1的4×4的方格网中,将任意连接两个格点的线段称作“格点线”,则“格点线”的长度不可能等于()A. B. C. D.11、如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当D PMN周长取最小值时,则∠MPN的度数为()A.140°B.100°C.50°D.40°12、下列说法中不正确的是()A.有两个角相等的三角形为等腰三角形B.等腰三角形两底角相等C.钝角三角形不可能是等腰三角形D.有一高线一中线重合的三角形是等腰三角形13、若菱形的周长为8,高为1,则菱形两邻角的度数比为()A.3:1B.4:1C.5:1D.6:114、如图,在中,,垂直平分,若,则的度数等于()A. B. C. D.15、如图,在中,平分.边的垂直平分线分别交于点.以下说法错误的是()A. B. C. D.二、填空题(共10题,共计30分)16、求图中直角三角形中未知的长度:b=________,c=________.17、如图,在矩形ABCD中,AB= ,E是BC的中点,AE⊥BD于点F,则CF的长是________.18、如图,已知的半径为4,弦垂直平分半径,与围成阴影部分,则S=________.阴影19、如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为________.20、如图,已知OA=OB,那么数轴上点A所表示的数是________.21、“健康荆州,你我同行”,市民小张积极响应“全民健身动起来”号召,坚持在某环形步道上跑步,已知此步道外形近似于如图所示的,其中,AB与BC 间另有步道DE相连,D地在AB的正中位置,E地与C地相距1km,若,小张某天沿路线跑一圈,则他跑了________km.22、如图,OP=1,过P作PP1⊥OP,得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;……依此法继续作下去,得OP2016=________.23、如图,已知点是的直径上的一点,过点作弦,使.若的度数为40°,则的度数是________.24、如图,中,,,小明要将该三角形分割成两个直角三角形和两个等腰三角形,他想出了如下方案:在上取点,过点画交于点,连结,在上取合适的点,连结可得到4个符合条件的三角形,则满足条件的长是________.25、如图,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E.若BC=15 cm,则△DEB的周长为________三、解答题(共5题,共计25分)26、已知:如图,四边形ABCD是⊙O的内接矩形,AB=4,BC=3,点E是劣弧上的一点,连接AE,DE.过点C作⊙O的切线交线段AE的延长线于点F,若∠CDE=30°,求CF的长.27、如图,一木杆原来垂直于地面,在离地某处断裂,木杆顶部落在离木杆底部5米处,已知木杆原长25米,求木杆断裂处离地面多少米?28、如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.29、如图所示,在一棵树的米高的处有两只猴子,一只猴子爬下树走到离树米的处.另一只猴子爬到树顶处后顺绳子滑到处,如果两只猴子所经过的距离相等,求这棵树的高.30、如图,在△ABC 中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,AD=AE,且 BE=.试说明:AB 平分∠EAD.参考答案一、单选题(共15题,共计45分)1、C2、A3、C4、C5、C6、D8、A9、A10、C11、B12、C13、C14、C15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、下列命题:①关于某条直线成轴对称的两个图形是全等图形;②有一个外角为60°的等腰三角形是等边三角形;③关于某直线对称的两条线段平行;④正五边形有五条对称轴;⑤在直角三角形中,30°角所对的边等于斜边的一半.其中正确的有()个.A.1个B.2个C.3个D.4个2、在菱形ABCD中,∠ABC=60°,AB=1,E为边BC的中点.则对角线BD上的动点P到E、C两点的距离之和的最小值为()A. B. C. D.3、如图,▱ABCD的对角线AC与BD相交于点O,AC⊥BC,且AB=10,AD=6,则OB的长度为()A.2B.4C.8D.44、如图,在△ABC 中,AB=20cm,AC=12cm,点 P 从点 B 出发以每秒 3cm 的速度向点 A 运动,点 Q 从点 A 同时出发以每秒 2cm 的速度向点 C 运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ 是以 PQ 为底的等腰三角形时,运动的时间是( )A.2.5 秒B.3 秒C.3.5 秒D.4 秒5、如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD 的长为( )A.1B.1.5C.2D.46、已知等腰三角形的一边长为4cm,另一边长为9cm,则它的周长为()A.13cmB.17cmC.22cmD.17cm或22cm7、若等腰三角形中有两边长分别为2和5,则这个三角形的周长为()A.9B.12C.7或9D.9或128、如图,在中,,为斜边的中点,在内绕点转动,分别交边,于点,(点不与点,重合),下列说法正确的是()①;②;③A.①②B.①③C.②③D.①②③9、直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为()A.90B.120C.121D.不能确定10、如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是()A.5B.6C.7D.811、如图所示,在矩形中,,点在边上,平分,,垂足为,则等于()A. B.1 C. D.212、有下列说法:①有一个角为60°的等腰三角形是等边三角形;②两条平行线之间的距离处处相等;③三边长为,,9的三角形为直角三角形;④长方体、直六棱柱、圆锥都是多面体。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)
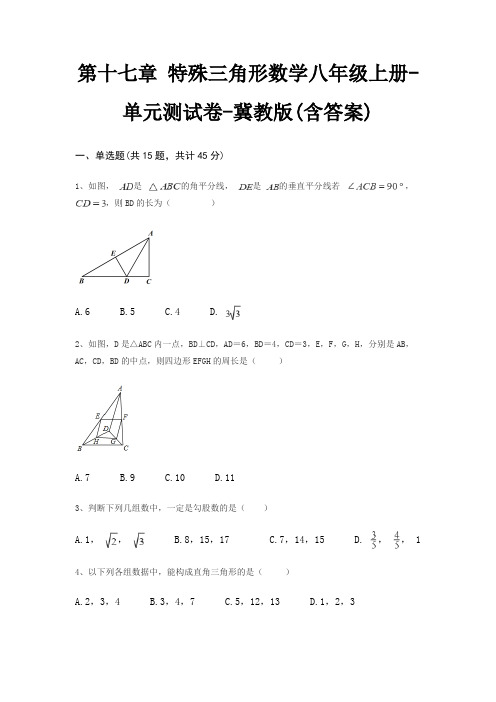
第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、如图,是的角平分线,是的垂直平分线若,,则BD的长为()A.6B.5C.4D.2、如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H,分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是()A.7B.9C.10D.113、判断下列几组数中,一定是勾股数的是()A.1,,B.8,15,17C.7,14,15D. ,, 14、以下列各组数据中,能构成直角三角形的是()A.2,3,4B.3,4,7C.5,12,13D.1,2,35、如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE 的长为()A.1B.2C.D.1+6、若等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是()A.15cmB.20cmC.25cmD.20cm或25cm7、如图,矩形ABCD的对角线AC与BD相交于点O,∠ADB=30°,AB=2018,则AD=( )A.1009B.2018C.1009D.20188、一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O 到水面的距离OC是()A.4B.5C.6D.89、如图,△ABC 中,AB=AC,AD 是∠BAC 的平分线,已知 AB=5,AD=3,则 BC的长为()10、菱形的周长为20cm,两个相邻的内角的度数之比为1:2,则较长的对角线的长度是()A.20 cmB.5 cmC. cmD.5 cm11、如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=,则下列结论:①∠DGA=∠CGF;②△DAG∽△CGF;③AB=2;④BE= CF.正确的个数是()A.2个B.3个C.4个D.5个12、如图,∠B=30°,线段BC=2,点E、F分别是线段BC和射线BA上的动点,设,则的最小值是()A.1B.2C.3D.413、一个长方形抽屉长12厘米,宽9厘米,贴抽屉底面放一根木棒,那么这根木棒最长(不计木棒粗细)可以是()A.15厘米B.13厘米C.9厘米D.8厘米14、下列命题:有一边相等的两个等腰三角形全等;面积相等的两个三角形全等;钝角三角形的三条高线所在直线的交点在三角形内;等腰三角形两底角的平分线相等其中真命题的个数有(15、等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为()A.50°B.130°C.50°或130°D.55°或130°二、填空题(共10题,共计30分)16、如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是________cm.17、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,若AC=6,tanB=,则CE =________.18、如图所示,在△ABC中,AB=AC,点D,E,F在边BC上,且∠BAD=∠CAD,BE=CF,AD⊥BC,则图中共有________组全等三角形.19、如图,矩形ABCD的两条对角线相交于点O,若,,则AC的长为________.20、如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是________ .21、如图,菱形ABCD的两条对角线AC,四交于点O,若,,则菱形ABCD 的周长为________。
第十七章 特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)

第十七章特殊三角形数学八年级上册-单元测试卷-冀教版(含答案)一、单选题(共15题,共计45分)1、判断以下各组线段为边作三角形,可以构成直角三角形的是()A.1,1,2B.3,4,5C.2,3,4D.4,5,62、已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有()A.②B.①②C.①③D.②③3、如图,有两棵树分别用线段AB和CD表示,树高AB=15米,CD=7米,两树间的距离BD=6米,一只鸟从一棵树的树梢(点A)飞到另一棵树的树梢(点C),则这只鸟飞行的最短距离AC=()A.6米B.8米C.10米D.12米4、直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图那样折叠,使点A与点B 重合,折痕为DE,则DE的长为()A. B.5 C. D.5、如图,已知正方形的边长为4,点是正方形的边上的一点,把△ABE沿BE翻折到△FBE,若,则DF的长为()A.2B.C.D.6、如图,A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则点P的坐标不可能是( )A.(2,0)B.(4,0)C.(-2 ,0)D.(3,0)7、已知△ABC中,∠C=90°,tanA= ,D是AC上一点,∠CBD=∠A,则sin∠ABD=()A. B. C. D.8、如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为()A. B. C. D.9、如图,正方形ABCD中,点E,F分别在AD,DC上,且△BEF为等边三角形,下列结论:①DE=DF;②∠AEB=75°;③BE= DE;④AE+FC=EF.其中正确的结论个数有()A.1个B.2个C.3个D.4个10、如图,在第一个△ABA1中∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则以点A4为顶点的等腰三角形的底角的度数为()A.175°B.170°C.10°D.5°11、如图,在四边形ABCD中,∠A=90°,AB=3 ,AD= ,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值为()A. B.3.5 C.5 D.2.512、如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是()A.4个B.5个C.8个D.9个13、等腰三角形的一个内角是50°,则另外两个角的度数分别是()A.65°,65°B.50°,80°C.65°,65°或50°,80° D.50°,50°14、在正方形网格中,∠BAC如图放置,点A,B,C都在格点上,则sin∠BAC的值为( )A. B. C. D.15、如图是用直尺和一个等腰直角三角尺画平行线的示意图,图中∠a的度数为()A.45°B.60°C.90°D.135°二、填空题(共10题,共计30分)16、如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若AD=4,CD=2,则AB的长是________.17、等腰△ABC中,AB=AC=10cm,BC=12cm,则BC边上的高是________cm.18、小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm),请你帮小华算出圆盘的半径是________cm.19、如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为________.20、等腰△ABC中,AB=AC,AC边上中线BD将△ABC的周长分成15和6两部分,则等腰△ABC的腰AB的长为________.21、如图,是⊙O的直径,C是⊙O上一点,的平分线交⊙O于D,且,则的长为________.22、将面积为2π的半圆与两个正方形拼接成如图所示的图形,则这两个正方形面积的和为________.23、等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为________24、如图,四边形是菱形,点分别在边上,其中是对角线上的动点,若的最小值为,则该菱形的面积为________25、已知等腰三角形两边的长分别是和,则它的周长是________ .三、解答题(共5题,共计25分)26、已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.27、如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P 是射线GC上一点,连接FP,EP,求证:FP=EP.28、如图,在△ABD中,D=90°, C是BD上一点,已知BC=9,AB=17,AC=10,求AD的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17章特殊三角形单元测试一、单选题(共10题;共30分)1.在下列几组数中不能作为直角三角形的三边长的是()A、7,24,25B、7,12,15C、5,12,13D、3,4,52.Rt△ABC中,已知∠C=90°, ∠A=30°,BD是∠B的平分线,AC=18,则BD的值为()A、4.9B、9C、12D、153.已知等腰△ABC中,AD⊥BC于点D,且AD=12BC,则△ABC底角的度数为()A.45°B.75°C.45°或15°或75°D.60°4.用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”应先假设:在一个三角形中()A.至多有一个内角大于或等于60°B.至多有一个内角大于60°C.每一个内角小于或等于60°D.每一个内角大于60°5.用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为()A.a,b都能被3整除B.a不能被3整除C.a,b不都能被3整除D.a,b都不能被3整除6.用反证法证明“a<b”时应假设()A.a>bB.a≤bC.a=bD.a≥b7.如图所示的正方形网格中,网格线的交点称为格点、已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是()A.6B.7C.8D.98.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为()A、30°B、36°C、40°D、45°9.等腰三角形底边上的高为8,周长为32,则三角形的面积为()A、56B、48C、40D、3210.如图,在Rt△ABC中,∠ACB=90°,AB= ,BC=2,则这个直角三角形的面积为()A、3B、6C、D、二、填空题(共8题;共24分)11.如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DE∥AC交AB于点E,若AB=8,则DE= ________12.如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长 ________13.按下列数据的规律填写:3,4,5,12,13,84,85,3612,________ ,…、14.反证法证明“三角形中至少有一个角不少于60°”先应假设这个三角形中________、15.等腰三角形的一个外角是100°,则这个等腰三角形的底角为________、16.如图,一架5米长的梯子AB,斜靠在一堵竖直的墙AO上,这时梯顶A距地面4米,若梯子沿墙下滑1米,则梯足B外滑________米、17.如图,已知一根长8m的竹竿在离地3m处断裂,竹竿顶部抵着地面,此时,顶部距底部有________ m、18.如下图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了________cm;三、解答题(共6题;共46分)19.如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E、求证:DE=DF、20.如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,求证:△DBE是等腰三角形、21.求证:任意三角形的三个外角中至多有一个直角、22.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a=S△ACD+S△ABC= 12 b2+ 12 a b、∵S四边形ADCB又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)∴a2+b2=c2请参照上述证法,利用图2完成下面的证明、将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°、求证:a2+b2=c2、23.已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积、24.如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长、答案解析一、单选题1、【答案】B【考点】勾股定理的逆定理【解析】【分析】分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形、【解答】A、∵72+242=49+576=625,252=625,∴72+242=252,则7,24,25能构成直角三角形;B、∵72+122=49+144=293,152=225,∴72+122≠152,则7,12,15不能构成直角三角形;C、∵52+122=25+144=169,132=169,∴52+122=132,则5,12,13能构成直角三角形;D、∵32+42=9+16=25,52=25,∴32+42=52,则5,4,3能构成直角三角形、故选B、【点评】主要考查了利用勾股定理的逆定理判定直角三角形的方法、在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断、2、【答案】C【考点】含30度角的直角三角形【解析】【分析】由题目可知,Rt△ABC中,∠C=90°, ∠A=30°,所以∠ABC=60°,又BD是∠B的平分线,所以∠ABD=30°,所以AD=BD。
因为在Rt△BCD中,∠C=90°,∠CBD=30°,∠BDC=60°,所以CD:BD=1:2,即CD:AD=1:2,又AC=18,所以BD=AD=12,故选C.【点评】通过直角三角形其中一个角为30°,得出此角所对应直角边为斜边的一半,根据此定理来解答此类题目。
3、【答案】C【考点】含30度角的直角三角形【解析】【解答】解:①如图1,点A是顶点时,∵AB=AC,AD⊥BC,∴BD=CD,∵AD=12BC,∴AD=BD=CD,在Rt△ABD中,∠B=∠BAD=12(180°﹣90°)=45°;②如图2,点A是底角顶点,且AD在△ABC外部时,∵AD=12BC,AC=BC,∴AD=12AC,∴∠ACD=30°,∴∠BAC=∠ABC=12×30°=15°;②如图2,点A是底角顶点,且AD在△ABC内部时,∵AD=12BC,AC=BC,∴AD=12AC,∴∠C=30°,∴∠BAC=∠ABC=12(180°﹣30°)=75°;综上所述,△ABC底角的度数为45°或15°或75°、故选C、【分析】作出图形,分①点A是顶点时,根据等腰三角形三线合一的性质可得BD=CD,从而得到AD=BD=CD,再利用等边对等角的性质可得∠B=∠BAD,然后利用直角三角形两锐角互余求解即可;②点A是底角顶点时,根据直角三角形30°角所对的直角边等于斜边的一半求出∠C=30°,然后再根据等腰三角形两底角相等求解即可、4、【答案】D【考点】反证法【解析】【解答】解:用反证法证明:在一个三角形中,至少有一个内角小于或等于60°,可以假设在一个三角形中,每个内角都大于60°、故选:D、【分析】根据反证法的证明方法,先假设命题的结论不成立,即假设在一个三角形中,每个内角都大于60°、5、【答案】D【考点】反证法【解析】【解答】解:反证法证明命题时,应假设命题的反面成立、“a,b中至少有一个能被3整除”的反面是:“a,b都不能被3整除”,故应假设a,b都不能被3整除、故选D、【分析】“a,b中至少有一个能被3整除”的对立面是:“a,b都不能被3整除”,得到假设、6、【答案】D【考点】反证法【解析】【解答】解:a,b的大小关系有a>b,a<b,a=b三种情况,因而a<b的反面是a≥b、因此用反证法证明“a<b”时,应先假设a≥b、故选D、【分析】反证法的步骤中,第一步是假设结论不成立,反面成立,可据此进行判断;需注意的是a<b的反面有多种情况,应一一否定、7、【答案】C【考点】等腰三角形的判定【解析】【解答】解:如上图:分情况讨论、①AB为等腰△ABC底边时,符合条件的C点有4个;②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个、故选:C、【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰△ABC底边;②AB为等腰△ABC其中的一条腰、8、【答案】B【考点】等腰三角形的性质【解析】【解答】解:∵AB=AC,∴∠B=∠C,∵AB=BD,∴∠BAD=∠BDA,∵CD=AD,∴∠C=∠CAD,∵∠BAD+∠CAD+∠B+∠C=180°,∴5∠B=180°,∴∠B=36°故选:B、【分析】求出∠BAD=2∠CAD=2∠B=2∠C的关系,利用三角形的内角和是180°,求∠B,9、【答案】B【考点】等腰三角形的性质,勾股定理【解析】【解答】解:过点A做AD⊥BC于点D,∵等腰三角形底边上的高为8,周长为32,∴AD=8,设DC=BD=x,则AB= (32﹣2x)=16﹣x,∴AC2=AD2+DC2,即(16﹣x)2=82+x2,解得:x=6,故BC=12,则△ABC的面积为:×AD×BC= ×8×12=48、故选:B、【分析】根据题意画出图形,进而利用勾股定理得出DC的长,进而求出BC的长,即可得出答案、10、【答案】A【考点】勾股定理【解析】【解答】解:∵在Rt△ABC中,∠ACB=90°,AB= ,BC=2,∴AC= =3,∴这个直角三角形的面积= AC•BC=3,故选A、【分析】利用勾股定理易求AC的长,进而可求出这个直角三角形的面积、二、填空题11、【答案】4【考点】等腰三角形的判定【解析】【解答】解:∵AD是∠BAC的平分线,∴∠CAD=∠BAD,∵DE∥AC,∴∠CAD=∠ADE,∴∠ADE=∠BAD,∴AE=DE,∵BD⊥AD,∴∠ADE+∠BDE=∠BAD+∠ABD=90°,∴∠ABD=∠BDE,∴DE=BE,∴DE=12AB,∵AB=8,∴DE=12×8=4、故答案为:4、【分析】根据角平分线的定义可得∠CAD=∠BAD,再根据两直线平行,内错角相等可得∠CAD=∠ADE,然后求出∠ADE=∠BAD,根据等角对等边可得AE=DE,然后根据等角的余角相等求出∠ABD=∠BDE,根据等角对等边可得DE=BE,从而得到DE=12A B、12、【答案】27d【考点】勾股定理【解析】【解答】证明:∵OD=OC,∴O在CD的垂直平分线线上,∠ODC=∠OCD,∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠ADC=∠BCD=90°,∴∠ADC﹣∠ODC=∠BCD﹣∠OCD,即∠ADO=∠BCO,在△ADO和△BCO中,∴△ADO≌△BCO(SAS),∴OA=OB,∴O在AB的垂直平分线上,过O作MN⊥AB与N交CD于M,如图所示:则AN=BN,NM⊥CD,OM=3d,ON=d,∴BC=MN=3d+d=4d,BN=∴AB=AN+BN=23d,∴AC=故答案为:27d、【分析】由等腰三角形的性质求出∠OBC=∠OCB,由矩形的性质求出AD=BC,∠ABC=∠DCB=90°,求出∠ABO=∠DCO,根据SAS推出△ABO≌△DCO,得出OA=OB,过O作MN⊥AB与N交CD于M,则AN=BN,NM⊥CD,OM=3d,ON=d,由勾股定理求出BN,得出AB,再由勾股定理求出AC即可、13、【答案】3613【考点】勾股数【解析】【解答】解:第一组勾股数为:3、4、5,第二组勾股数为:5、12、13,第三组勾股数为:13、84、85,由第二组与第三组可以看出后两个数相差1,所以第四组为:85、3612、3613、故答案为:3613、【分析】根据勾股数排列的规律可以看出:第二组勾股数为:5、12、13,第三组为:13、84、85,后两个数相差1,所以第四组为:85、3612、3613、14、【答案】每个内角都小于60°【考点】反证法【解析】【解答】解:∵用反证法证明三角形中至少有一个角不小于60°,∴第一步应假设结论不成立,即三角形的三个内角都小于60°、故答案为:每个内角都小于60°、【分析】熟记反证法的步骤,从命题的反面出发假设出结论,直接填空即可、15、【答案】50°或80°【考点】等腰三角形的性质【解析】【解答】解:①若100°的外角是此等腰三角形的顶角的邻角,则此顶角为:180°﹣100°=80°,则其底角为:180∘−80∘2 =50°;②若100°的外角是此等腰三角形的底角的邻角,则此底角为:180°﹣100°=80°;故这个等腰三角形的底角为:50°或80°、故答案为:50°或80°、【分析】由等腰三角形的一个外角是100°,可分别从①若100°的外角是此等腰三角形的顶角的邻角与②若100°的外角是此等腰三角形的底角的邻角去分析求解,即可求得答案、16、【答案】1【考点】勾股定理的应用【解析】【解答】解:在Rt△ABO中,根据勾股定理知,BO= AB2−AO2 =3(m),在Rt△COD中,根据勾股定理知,DO= CD2−CO2 =4(m),所以BD=DO﹣BO=1(米)、故答案为:1、【分析】梯子的长是不变的,只要利用勾股定理解出梯子滑动前和滑动后的所构成的两直角三角形即可、17、【答案】4【考点】勾股定理的应用【解析】【解答】解:由图形及题意可知,AB2+BC2=AC2设旗杆顶部距离底部有x米,有32+x2=52,得x=4,故答案为4、【分析】利用勾股定理,用一边表示另一边,代入数据即可得出结果、18、【答案】2【考点】勾股定理【解析】【解答】解:Rt△ACD中,AC= AB=4cm,CD=3cm;根据勾股定理,得:AD=BD= =5cm;∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;故橡皮筋被拉长了2cm、【分析】根据勾股定理,可求出A D、BD的长,则AD+BD﹣AB即为橡皮筋拉长的距离、三、解答题19、【答案】证明:∵AB=AC,∴∠B=∠C,∵DE⊥AB,DF⊥AC,∴∠BFD=∠CED=90°,∵BD=DC,∴△BDF≌△CDE,∴DE=DF、【考点】等腰三角形的性质【解析】【分析】要证DE =DF ,只需证△BDF ≌△CDE ,已知AB =AC ,可得∠B =∠C ,又已知BD =DC ,∠BFD =∠CED =90°,则两三角形全等可证、 20、【答案】证明:在△ABC 中,BA =BC , ∵BA =BC , ∴∠A =∠C , ∵DF ⊥AC , ∴∠C +∠FEC =90°, ∠A +∠D =90°, ∴∠FEC =∠D , ∵∠FEC =∠BED , ∴∠BED =∠D , ∴BD =BE ,即△DBE 是等腰三角形、 【考点】等腰三角形的判定【解析】【分析】首先根据等腰三角形的两个底角相等得到∠A =∠C ,再根据等角的余角相等得∠FEC =∠D ,同时结合对顶角相等即可证明△DBE 是等腰三角形、 21、【答案】证明:假设任意三角形的三个外角中有2个直角, 因为两个外角为直角,则相邻两个内角也为90°, 再加上一个角一定大于180°, 与三角形内角和为180°矛盾,所以任意三角形的三个外角中至多有一个直角、 【考点】反证法【解析】【分析】用反证法进行证明;先设任意三角形的三个外角中有2个直角,然后得出假设与三角形内角和定理相矛盾,从而证得原结论成立、22、【答案】证明:连结BD ,过点B 作DE 边上的高BF ,则BF =b ﹣a ,∵S 五边形ACBED =S △ACB +S △ABE +S △ADE = ab + b 2+ ab ,又∵S 五边形ACBED =S △ACB +S △ABD +S △BDE = ab +c 2+a (b ﹣a ),∴ab +b 2+ab =ab +c 2+ a (b ﹣a ),∴a 2+b 2=c 2 、【考点】勾股定理的证明【解析】【分析】首先连结BD,过点B作DE边上的高BF,则BF=b﹣a,表示出S五边形ACBED,两者相等,整理即可得证、23、【答案】解:连接A C、∵∠ABC=90°,AB=1,BC=2,∴AC= = ,在△ACD中,AC2+CD2=5+4=9=AD2,∴△ACD是直角三角形,= AB•BC+ AC•CD,∴S四边形ABCD= ×1×2+ ××2,=1+ 、故四边形ABCD的面积为1+ 、【考点】勾股定理,勾股定理的逆定理【解析】【分析】先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可、24、【答案】解:在Rt△ABC中,∠ACB=90°,AC=8m,BC=6m,由勾股定理有:AB=10m,应分以下三种情况:①如图1,当AB=AD=10m时,∵AC⊥BD,∴CD=CB=6m,∴△ABD的周长=10+10+2×6=32(m)、②如图2,当AB=BD=10m时,∵BC=6m,∴CD=10﹣6=4m,∴AD= = =4 (m),∴△ABD的周长=10+10+4 =(20+4 )m、③如图3,当AB为底时,设AD=BD=x,则CD=x﹣6,∵由勾股定理得:AD2=AC2+CD2=82+(x﹣6)2=x2,解得x= 、∴△ABD的周长为:AD+BD+AB= + +10= (m)、综上所述,扩充后的等腰三角形绿地的周长为:32m或(20+4 )m或m、【考点】等腰三角形的判定,勾股定理的应用【解析】【分析】根据题意画出图形,构造出等腰三角形,根据等腰三角形及直角三角形的性质利用勾股定理解答、。
