有限元课程实训结课上机参考例题
有限元法基础及应用实验上机报告实例

一,实验描述:1、本作业属于哪类问题在本作业中,根据板的结构特点和受力情况,确定该问题属于平面对称应力问题,定义分析类型为静力学分析。
2、本文采用如何的单位制本题中,长度单位为m,故为方便起见,采用力的单位为N,压强的单位为pa,时间的单位为s,质量的单位为kg。
3、单元类型:对单元描述;材料;实常数单元类型为选取shell Elastic 4node63单元材料:弹性模量为2.1e11pa,泊松比为0.33。
由题意确定时常数,即厚度为0.1m4、划分网格。
网格划分设置。
单元数,节点数。
网格化分设置:设置单元边长值为0.1m,指定单元形状为Areas。
5、加载描述(1)对整体模型,首先对四周固定端加载位移约束,设定其位移值为0;然后,对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
(2)对四分之一模型,首先对两边固定端加载位移约束,设定其位移值为0;然后,对两坐标轴所在的边施加对称载荷,最后对面施加面载荷,设置面载荷为20000N;接着将施加在实物体上的载荷转换到有限元模型上,并显示施加在有限元模型上的载荷。
加载完后,对该有限元模型进行求解。
6、后处理:最大MISIS应力和最大位移的位置和大小。
绘制结构的应力和变形图。
二,实验步骤(一)绘制整体实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,结果如下:边界条件施加载荷20000N/m求解以后4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图从图中可以看出其中实体边界中点位置的应力最大为0.583e+07pa,最大变形在中间圆弧的位置,0.144e-3m(二)绘制四分之一的实体模型1,在ANSYS中构造实体模型,如下图所示2,根据结构特点及所受载荷地情况,选取shell Elastic 4node63单元,设置材料常数:弹性模量E=2.1e11,u=0.33,单元边值为0.1m对其进行网格剖分,网格划分图如下:3,正确施加载荷和边界条件,注意此处有一个对称载荷的加载,结果如下:4,绘制平板的应力和变形图,并给出最大应力和变形的位置及大小:应力图应变图三,实验小结这次ANSYS上机实验课是使用shell中的Elastic 4node63单元,这使我对ANSYS软件中的单元有了更深的认识,同时对平面问题的静力分析的基本思路和操作步骤更加熟悉。
有限元上机报告

有限元上机报告模板一、实验目的题目:图示折板上端固定,右侧受力F=1000N,该力均匀分布在边缘各节点上;板厚t=2mm,材料选用低碳钢,弹性模量E=210GPa,u=0.33。
此题属于平面应力问题,采用的单元类型为:Solid Quad-8node单位制:力(N)、弹性模量(MPa)、长度(mm)。
二、实体建模的方法1.定义矩形:Main Menu>Preprocessor>Modeling>Create>Areas>Rectangle>By Dimensions。
输入:X1=0,X2=30,Y1=0,Y2=60。
点击对话框上的Apply按钮创建第一个矩形。
输入X1=30,X2=60,Y1=0,Y2=30。
点击对话框上的OK按钮创建第二个矩形。
2. 面图元的加运算:Main Menu>Preprocessor>Modeling>Operate>Booleans>Add>Areas。
点击对话框上的Pick All按钮,所有的面被加在一起。
点击SAVE_DB保存数据。
三、单元类型1. 此题属于平面应力问题,采用Solid单元的Plane82。
2. 材料属性:弹性模量为21e4MPa,泊松比为0.33。
3. 实常数:板厚2mm。
四、划分网格以边长为2mm的正方形划分单元,总共有675个单元,736个节点。
具体操作如下:1. Main Menu >Preprocessor>Meshing>Mesh Tool.2. 在Mesh Tool面板上点击Size Controls模块内的Global Set 按钮,在弹出的对话框中输入Element edge length为2,按ok完成。
3. 在Mesh下拉框中选Areas。
4. 点击Mesh按钮网格划分,点击Pick All按钮,点击Close关闭Mesh Tool 面板。
有限元ansys上机考试题

如图所示的外伸梁,均布载荷的极度为q = 3kN/m,集中力偶之矩M = 3KNm,梁的截面如图所示,试求梁的内力和变形情况,画出梁的变形图(挠曲线),剪力图和弯矩图。
图示平面梁架,截面为0.1×0.1m2的矩形,弹性模量为2.1×1011Pa,泊松比为0.3。
施加在梁上的集中力F = 10000N。
试求梁架的内力,画出弯矩图与剪力图。
析当在左右臂两侧的突起面上作用以p = 1100Pa的压强时,整个结构的应力分布。
给出最大应力的值。
提示:因该结构几何、载荷均对称,可考虑取一半进行分析并注意对称面上施加合理的约束。
p p料的密度为7830kg/m3,试提取该结构的前10阶固有频率。
如图所示的带孔平板,已知q = 1000Pa,板厚为0.1m,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析平板受力后的变形及应力分布。
提示:单元类型选取带厚度的平面应力单元。
q6m如图所示的涵洞,作用均布载荷7500N/m2,试分析其受力情况。
材料的弹性模量为210GPa,泊松比0.3。
提示:单元类型选择平面应变,可考虑取一半涵洞建立模型。
如图所示的带孔钢制圆盘,已知p = 20MPa,弹性模量为2.1×1011Pa,泊松比为0.3。
若在孔内塞入一个高0.1m,直径为0.1m的铝制圆柱(取铝材的弹性模量为1.2×1011Pa,泊松比为0.3),试分析变形及应力。
p = 20MPa如图所示的带孔平板,已知板厚为1cm,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析平板受力后的变形及应力分布。
提示:单元类型选取带厚度的平面应力单元。
桥梁有关参数如图所示,弹性模量为2.1×1011Pa,泊松比为0.3。
试分析桥面作用向下均布力q=50kN/m时的整个结构变形及应力分布。
提示:单元类型斜拉索用Link单元,其他用梁单元。
或全部采用梁单元,可利用对称性取一半进行分析。
2013有限元上机作业题
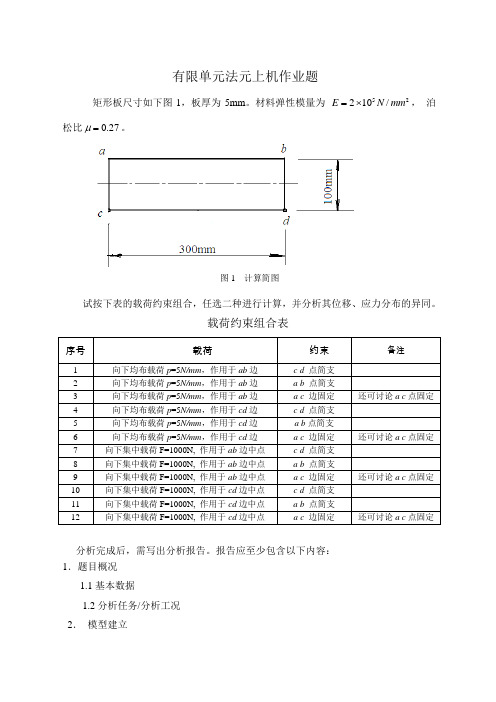
有限单元法元上机作业题
矩形板尺寸如下图1,板厚为5mm 。
材料弹性模量为 25/102mm N E ⨯=, 泊松比27.0=μ。
图1 计算简图
试按下表的载荷约束组合,任选二种进行计算,并分析其位移、应力分布的异同。
载荷约束组合表
分析完成后,需写出分析报告。
报告应至少包含以下内容:
1.题目概况
1.1基本数据
1.2 分析任务/分析工况 2. 模型建立
2.1 单元选择及其分析
2.2 模型建立及网格划分
2.3 载荷处理
3.计算分析
3.1 位移分布及其分析
3.2 应力分布及其分析
4.关于计算分析的体会,意见等
(注:封面上注明题目及其编号、姓名、班级、学号。
)
2013 年16月。
上海大学《有限元》2020年上机考题试题及答案

上海大学2020 ~2021 学年春季学期试卷 A 上机操作题课程名:有限元分析课程号:09A36012 学分: 3应试人声明:我保证遵守《上海大学学生手册》中的《上海大学考场规则》,如有考试违纪、作弊行为,愿意接受《上海大学学生考试违纪、作弊行为界定及处分规定》的纪律处分。
应试人应试人学号应试人所在院系六上机操作题(30分)目标:使用接触预测球(Ball)和窝(Socket)间的球形界面的压力形貌。
模型描述:●球窝连接2D轴对称模型和球窝连接3D四分之一模型●材料:钢对钢●接触:球形界面摩擦区域,摩擦系数=0.25●载荷和边界条件:窝固定在顶部,球的下部在-Y方向施加1000N力上机实验报告要求:1、简要写出主要的分析过程;针对2D轴对称模型和3D四分之一模型,哪些方面需要加以注意(6分);2、针对球窝连接2D轴对称模型,用总体单元尺寸分别为1.0和0.5mm划分网格,给出划分网格后的有限元模型图(4分);3、针对球窝连接2D轴对称模型,分别给出两种网格划分方式下结构的von-Mises应力云图及位移云图,并在云图上标示出最大值所发生的位置;用contact tool给出两种网格划分方式下接触面的接触压力云图。
(12分)。
4、针对球窝连接3D四分之一模型,用总体单元尺寸为0.75mm划分网格,并施加和2D 轴对称模型相同的载荷和边界条件,进行计算,给出划分网格后的有限元模型图,以及von-Mises应力云图及位移云图,并在云图上标示出最大值所发生的位置。
(6分)5、简单描述自己的心得体会。
(2分)上机实验报告:1.2D轴对称模型分析过程:打开workbench15.0,在左侧选择static structurl,材料为钢,在unite菜单中选择单位,然后鼠标右键点击geometry,选择properties,在analysis type中选择2D(在导入前设置为对称界面)如图:在geometry中导入ball-socket2D模型,并打开model,启动Mechanical,将作业单位制改为Metric(mm,Kg,s,mV,mA)改变部件特性为轴对称,选中Geometre,在Details of Geometry中把2D Behavior改为Axisymmetric修改接触行为,在contact of region里面选择Behavior为frictional,将fiction Coefficient修改为0.25执行网格划分,总体单元尺寸分别为1.0和0.5mm划分网格,在element size 填写0.5和1mm,得到以下网格划分:1mm 0.5mm选择static structural,右键选择球窝上边界,插入fixed support,选择球下边界插入load/force,在define by选择component,在y方向输入-1000选中solution,插入deformation total还有stress-equivalent(von mise),再插入contact tool,右键contact tool插入pressure。
有限元例题

q Fx 2 2 F2 Fy 2 0
K 11 K K 21 K 31 K 41
K 12 K 22 K 32 K 42
K 13 K 23 K 33 K 43
K 14 K 24 K 34 K 44
(3)零位移约束的处理,零位移处划行划列
K
K 22 K 32
K 22
K 32
K 23 K 33
线性方程组为:
K 23 2 F2 K 33 3 F3
1 2 1 1 2
(4)计算单元刚度矩阵 单元面积: A1 A2 (5)弹性矩阵:
D
E 1 2
1 0
1 0
0 3 1 0 3E 0 1 3 0 8 1 0 0 1 2
(6)几何矩阵:
B Bi
Bj
Bm
0 ci bi
b i 1 Bi 0 2A ci
2 u 2 q / 2 7 4 4 4 13 2 12 v 0 3Eh 2 7 0 u 3 q / 2 32 4 2 13 v3 0 2 12 0 u 2 1.98 v 2 q 0.36 u 3 Eh 1.79 v3 0.024
计算系数: 对于单元 1:
x1 0, y1 0,
a2 x3 y1 x1 y3 0, a3 x1 y 2 x2 y1 0, E K 332h 74
有限元习题及答案

有限元习题及答案有限元习题及答案有限元方法是一种常用的数值计算方法,用于求解各种工程和科学问题。
在学习有限元方法的过程中,练习习题是非常重要的,可以帮助学生巩固所学的知识,并提高解决实际问题的能力。
本文将介绍一些有限元习题及其答案,希望对学习有限元方法的同学有所帮助。
习题一:一维热传导问题考虑一个长度为L的一维杆,其两端固定,杆上的温度满足以下热传导方程:∂²T/∂x² = 0,其中T为温度,x为位置。
已知杆的两端温度分别为T1和T2,求解杆上的温度分布。
解答一:根据热传导方程,可以得到温度分布的一般解为T(x) = Ax + B,其中A和B为常数。
根据边界条件,可以得到方程组:T(0) = B = T1T(L) = AL + B = T2解方程组可得A = (T2 - T1) / L,B = T1。
因此,温度分布为T(x) = ((T2 - T1) / L) * x + T1。
习题二:二维弹性问题考虑一个矩形薄板,其长为L,宽为W,材料的弹性模量为E,泊松比为ν。
已知薄板的边界上施加了一定的边界条件,求解薄板上的位移场。
解答二:对于二维弹性问题,可以使用平面应力假设,即假设薄板内部的应力只有两个分量σx和σy,并且与z轴无关。
根据平面应力假设和胡克定律,可以得到位移场的偏微分方程:∂²u/∂x² + ν * (∂²u/∂y²) + (1 - ν) * (∂²v/∂x∂y) = 0∂²v/∂y² + ν * (∂²v/∂x²) + (1 - ν) * (∂²u/∂x∂y) = 0其中u和v分别为位移场在x和y方向上的分量。
边界条件根据具体情况给定。
通过数值方法,如有限元方法,可以求解位移场的近似解。
习题三:三维流体力学问题考虑一个三维流体力学问题,流体在一个封闭容器内流动,容器的形状为一个长方体,已知流体的速度场和压力场的初始条件,求解流体的运动状态。
有限元课程实训结课上机参考例题

有限元课程实训结课上机参考例题题 1:图1所示薄板左边固定,右边受均布压力P=100Kn/m 作用,板厚度为0.3cm ;试采用如下方案,对其进行有限元分析,并对结果进行比较。
(1)三节点三角形单元;(2个和200个单元)(2)四节点矩形单元; (1个和50个单元)(3)八节点等参单元。
(1个和20个单元)图 1 题 2:图2所示为一带圆孔的单位厚度(1M )的正方形平板,在x 方向作用均布压力0.25Mpa ,试用三节点常应变单元和六节点三角形单元对平板进行有限元分析,并对以下几种计算方案的计算结果进行比较:(1) 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;注:在y 轴上,孔边应力的精确解为:MPa x 75.0-=σ,在x 轴上,孔边应力的精确解为:MPa y 25.0=σ图 2题 3:图3所示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)图 3题 4:图4所示为一隧道断面,其内受均布水压力q,外受土壤均布压力p;试采用不同单元计算断面内的位移及应力,并分别分析q=0或p=0时的位移和应力分布情况。
(材料为钢,隧道几何尺寸和压力大小自行确定)图 4题 5:图5所示一简化直齿轮轮齿截面,高h=60mm,齿根宽b=60mm,齿顶宽c=25mm,齿顶作用力P=10Kn;试采用不同单元分析轮齿上位移及应力分布,并只指出最大应力位置。
图 5题 6:图6所示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元课程实训结课上机参考例题
题 1:图1所示薄板左边固定,右边受均布压力P=100Kn/m 作用,板厚度为0.3cm ;试采用如下方案,对其进行有限元分析,并对结果进行比较。
(1)三节点三角形单元;(2个和200个单元)
(2)四节点矩形单元; (1个和50个单元)
(3)八节点等参单元。
(1个和20个单元)
图 1 题 2:图2所示为一带圆孔的单位厚度(1M )的正方形平板,在x 方向作用均布压力0.25Mpa ,试用三节点常应变单元和六节点三角形单元对平板进行有限元分析,并对以下几种计算方案的计算结果进行比较:
(1) 分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;
(2)分别采用不同数量的三节点常应变单元计算;
注:在y 轴上,孔边应力的精确解为:MPa x 75.0-=σ,在x 轴上,孔边应力的精确解为:MPa y 25.0=σ
图 2
题 3:图3所示为带方孔(边长为80mm)的悬臂梁,其上受部分均布载荷(p=10Kn/m)作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为1mm,材料为钢)
图 3
题 4:图4所示为一隧道断面,其内受均布水压力q,外受土壤均布压力p;试采用不同单元计算断面内的位移及应力,并分别分析q=0或p=0时的位移和应力分布情况。
(材料为钢,隧道几何尺寸和压力大小自行确定)
图 4
题 5:图5所示一简化直齿轮轮齿截面,高h=60mm,齿根宽b=60mm,齿顶宽c=25mm,齿顶作用力P=10Kn;试采用不同单元分析轮齿上位移及应力分布,并只指出最大应力位置。
图 5
题 6:图6所示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:
(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;
(2)分别采用不同数量的三节点常应变单元计算;
(3)当选常应变三角单元时,分别采用不同划分方案计算。
图 6。
