矩阵范数理论及其应用
矩阵范数详解

向量和矩阵的范数的若干难点导引矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵m nA C ⨯∈可以视为一个mn 维的向量(采用所谓“拉直”的变换),所以,直观上可用mnC上的向量范数来作为m nA C⨯∈的矩阵范数。
比如在1l -范数意义下,111||||||m niji j A a===∑∑()12tr()HA A =; (1.1)在2l -范数意义下,12211||||||m n F ij i j A a ==⎛⎫= ⎪⎝⎭∑∑, (1.2)注意这里为了避免与以后的记号混淆,下标用“F ”,这样一个矩阵范数,称为Frobenius范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了?因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB 的“大小”相对于A B 与的“大小”关系。
定义1 设m nA C ⨯∈,对每一个A ,如果对应着一个实函数()N A ,记为||||A ,它满足以下条件:(1)非负性:||||0A ≥;(1a )正定性:||||0m nA O A ⨯=⇔=(2)齐次性:||||||||||,A A C ααα=∈;(3)三角不等式:||A ||||||||||||,m n A B A B B C ⨯+≤+∀∈则称()||||N A A =为A 的广义矩阵范数。
进一步,若对,,m n n l m lC C C ⨯⨯⨯上的同类广义矩阵范数||||∙,有(4)(矩阵相乘的)相容性:||A ||||||||||||AB A B ≤, n lB C ⨯∈, 则称()||||N A A =为A 的矩阵范数。
我们现在来验证前面(1.1)和(1.2)定义的矩阵范数是否合法?我们这里只考虑(1.2),把较容易的(1.1)的验证留给同学们,三角不等式的验证。
带虚数的矩阵范数

带虚数的矩阵范数带虚数的矩阵范数是一种常见的数学概念,它在矩阵理论和线性代数中有着广泛的应用。
虚数在数学中是一种特殊的数,它可以表示为实数与虚数单位i的乘积。
而矩阵范数则是用来衡量矩阵的大小或者变化程度的一种方式。
带虚数的矩阵范数结合了虚数与矩阵的概念,具有一定的特殊性和重要性。
我们来了解一下什么是矩阵范数。
矩阵范数是一种将矩阵映射到实数或复数的函数,它可以用来衡量矩阵的大小或者变化程度。
常见的矩阵范数有Frobenius范数、谱范数和算子范数等。
不同的矩阵范数在不同的应用场景下有着不同的意义和计算方法。
而带虚数的矩阵范数则是在矩阵范数的基础上,考虑了矩阵中可能存在的复数元素。
在实际问题中,很多矩阵的元素都是复数,而带虚数的矩阵范数可以更准确地描述这些矩阵的性质和特点。
例如,在量子力学中,矩阵经常用来表示物理系统的态矢量和算符,而这些矩阵往往具有复数元素,带虚数的矩阵范数可以用来度量这些矩阵的变化程度和大小。
带虚数的矩阵范数的计算方法与普通矩阵范数类似,只是在对矩阵进行求范数时,需要将复数元素的模加入到范数的计算中。
例如,对于一个复数矩阵A,其矩阵范数可以表示为:||A|| = max |λ|,其中λ是矩阵A的特征值。
而带虚数的矩阵范数可以表示为:||A|| = max |λ| + max |μ|,其中λ和μ分别是矩阵A的特征值的实部和虚部。
带虚数的矩阵范数可以更全面地衡量矩阵的大小和变化程度。
带虚数的矩阵范数在实际应用中具有重要的意义。
例如,在信号处理中,矩阵常用来表示信号的相关性和相似性。
而带虚数的矩阵范数可以用来度量信号之间的差异和变化程度,从而为信号处理提供了有效的工具和指标。
带虚数的矩阵范数还可以用于矩阵的优化和近似计算。
在机器学习和数据挖掘中,矩阵的优化和近似计算是非常重要的问题。
而带虚数的矩阵范数可以用来度量矩阵的优化程度和近似误差,从而帮助我们选择合适的优化算法和近似方法。
带虚数的矩阵范数是一种重要的数学概念,在矩阵理论和线性代数中具有广泛的应用。
矩阵范数详解.docx

《周国标师生交流讲席010》向量和矩阵的范数的若干难点导引(二)一.矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵A C m n可以视为一个mn维的向量(采用所谓“拉直”的变换),所以,直观上可用C mn上的向量范数来作为A C m n的矩阵范数。
比如m n 1在∣1 -范数意义下,IIAl1 ;二Ia ijI= tr(A H A) 2; (1.1 )1Zl mn A2在I2-范数意义下,∣∣A∣∣F=∑∑同|2,(1.2)Iy j A J注意这里为了避免与以后的记号混淆,下标用“F”,这样一个矩阵范数,称为Frobenius范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了?因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB的“大小”相对于A与B的“大小”关系。
定义1设A C mn,对每一个A ,如果对应着一个实函数N(A),记为IlAll ,它满足以下条件:(1)非负性:|| A||_0 ;(1 a)正定性:A=O mn= IIAII= 0(2)齐次性:||〉A||=| |||A||, • C ;(3)三角不等式:||A||A B||—||A|| ||B||, -B C m n则称N(A)=|| A||为A的广义矩阵范数。
进一步,若对C m n,C n 1C m l上的同类广义矩阵范数|| || ,有(4)(矩阵相乘的)相容性:|| A || AB ||_|| A|||| B ||, B C n I , 则称N(A) =||A||为A的矩阵范数。
我们现在来验证前面(1.1 )和(1.2 )定义的矩阵范数是否合法?我们这里只考虑(1.2 ),把较容易的(1.1 )的验证留给同学们,三角不等式的验证。
矩阵范数详解

《周国标师生交流讲席010》向量和矩阵的范数的若干难点导引(二)一. 矩阵范数的定义引入矩阵范数的原因与向量范数的理由是相似的,在许多场合需要“测量”矩阵的“大小”,比如矩阵序列的收敛,解线性方程组时的误差分析等,具体的情况在这里不再复述。
最容易想到的矩阵范数,是把矩阵m nA C ⨯∈可以视为一个mn 维的向量(采用所谓“拉直”的变换),所以,直观上可用mn C上的向量范数来作为m nA C⨯∈的矩阵范数。
比如在1l -范数意义下,111||||||mniji j A a===∑∑()12tr()HA A =; (1.1)在2l -范数意义下,12211||||||mnF ij i j A a ==⎛⎫= ⎪⎝⎭∑∑,(1.2)注意这里为了避免与以后的记号混淆,下标用“F ”,这样一个矩阵范数,称为Fro be nius 范数,或F-范数。
可以验证它们都满足向量范数的3个条件。
那么是否矩阵范数就这样解决了?因为数学上的任一定义都要与其对象的运算联系起来,矩阵之间有乘法运算,它在定义范数时应予以体现,也即估计AB 的“大小”相对于A B 与的“大小”关系。
定义1 设m nA C ⨯∈,对每一个A ,如果对应着一个实函数()N A ,记为||||A ,它满足以下条件:(1)非负性:||||0A ≥;(1a )正定性:||||0m nA O A ⨯=⇔=(2)齐次性:||||||||||,A A C ααα=∈;(3)三角不等式:||A ||||||||||||,m n A B A B B C ⨯+≤+∀∈则称()||||N A A =为A 的广义矩阵范数。
进一步,若对,,m nn l m l CC C ⨯⨯⨯上的同类广义矩阵范数||||•,有(4)(矩阵相乘的)相容性:||A ||||||||||||AB A B ≤, n lB C ⨯∈,则称()||||N A A =为A 的矩阵范数。
我们现在来验证前面(1.1)和(1.2)定义的矩阵范数是否合法?我们这里只考虑(1.2),把较容易的(1.1)的验证留给同学们,三角不等式的验证。
矩阵论范数知识点总结

矩阵论范数知识点总结一、概述矩阵论是线性代数的一个分支,它研究矩阵及其性质。
矩阵的范数是矩阵的一种性质的度量,它在矩阵分析、数值线性代数、优化理论等领域中有着广泛的应用。
本文将对矩阵范数的定义、性质、应用以及相关的其他知识点进行总结和介绍。
二、矩阵的定义在数学中,矩阵是一个按照矩形排列的复数或实数集合。
也可以看成是一个数域上的矩形阵列。
矩阵的元素可以是实数、复数或者是其他的数学对象。
一个n×n矩阵A是一个由n×n个元素(a_ij)组成的矩形数组。
三、范数的定义在数学中,范数是定义在向量空间中的一种函数,它通常被用来衡量向量的大小或长度。
对于矩阵来说,范数是一种度量矩阵大小的方法。
对于一个矩阵A,它的范数通常记作||A||。
矩阵的范数满足以下性质:1. 非负性:||A|| ≥ 0,并且当且仅当A = 0时,||A|| = 02. 齐次性:对于任意标量c,||cA|| = |c| * ||A||3. 三角不等式:||A+B|| ≤ ||A|| + ||B||四、矩阵范数的种类矩阵范数一般有几种不同的类型。
1. Frobenius范数:矩阵A的Frobenius范数定义为||A||_F = sqrt(Σ_(i=1)^m Σ_(j=1)^n|a_ij|^2)2. 1-范数:矩阵A的1-范数定义为||A||_1 = max(Σ_(i=1)^n |a_ij|)3. 2-范数:矩阵A的2-范数定义为||A||_2 = max(Σ_(i=1)^m Σ_(j=1)^n |a_ij|^2)^(1/2)4. ∞-范数:矩阵A的∞-范数定义为||A||_∞ = max(Σ_(j=1)^n |a_ij|)五、矩阵范数的性质矩阵范数具有一些重要的性质,下面将介绍其中一些主要性质。
1. 非负性:||A|| ≥ 0,并且当且仅当A = 0时,||A|| = 02. 齐次性:对于任意标量c,||cA|| = |c| * ||A||3. 三角不等式:||A+B|| ≤ ||A|| + ||B||4. 乘法范数:||AB|| ≤ ||A|| * ||B||5. 谱半径:对于任意矩阵A,它的谱半径定义为rho(A) = max|λ_i(A)|6. 对称矩阵:对于对称矩阵A,其2-范数定义为rho(A),即||A||_2 = rho(A),其中rho(A)是A的最大特征值六、矩阵范数的应用矩阵范数在数学和工程领域有着广泛的应用,下面将介绍一些主要的应用。
矩阵的欧几里得范数

矩阵的欧几里得范数1.引言1.1 概述矩阵的欧几里得范数是在线性代数中常用的一种范数,用来衡量矩阵的大小和变化幅度。
它是基于矩阵的元素进行计算的,并且具有一些重要的性质和应用。
在本文中,我们将首先给出矩阵的欧几里得范数的定义,然后介绍一些与之相关的性质。
通过深入探讨这些内容,我们将更好地理解欧几里得范数在矩阵计算中的意义和作用。
接下来,我们将总结欧几里得范数的应用,并讨论矩阵的欧几里得范数在实际问题中的重要性。
通过具体的例子和应用场景,我们将展示欧几里得范数在数据处理、优化算法等领域的广泛应用,以及它对矩阵的重要性和影响。
在本文的最后,我们将得出结论,总结矩阵的欧几里得范数的定义、性质和应用,并探讨其在实际问题中的重要性。
我们希望通过这篇文章能够为读者提供关于矩阵的欧几里得范数的全面了解,并激发读者对于矩阵范数和线性代数的兴趣。
1.2 文章结构文章结构部分的内容可以描述本文主体的组成和各个部分的内容安排,以帮助读者理解文章的结构和流程。
以下是一个可能的描述:在本文中,我们将对矩阵的欧几里得范数进行详细讨论。
文章分为三个主要部分:引言、正文和结论。
引言部分首先给出了本文的概述,简要介绍了矩阵的欧几里得范数的定义和性质,并说明了本文的目的。
正文部分是本文的核心内容,其中2.1小节给出了矩阵的欧几里得范数的定义。
我们将详细解释欧几里得范数的含义和计算方法,并讨论其在矩阵分析和应用中的重要性。
2.2小节将介绍欧几里得范数的一些基本性质,包括正定性、三角不等式、与矩阵转置的关系等。
我们将通过数学推导和实例说明这些性质的重要意义,并展示其在实际问题中的应用。
结论部分是对本文主要内容进行总结和延伸。
3.1小节总结了欧几里得范数的应用,强调了其在数据分析、优化问题等领域中的重要性。
3.2小节将进一步讨论矩阵的欧几里得范数在实际问题中的重要性,包括其在图像处理、机器学习等领域的应用,并提出了一些未来的研究方向。
通过以上文章结构的划分,读者可以清晰地了解到本文的篇章组织和各个部分的内容安排,更好地阅读和理解文章的主题。
矩阵范数
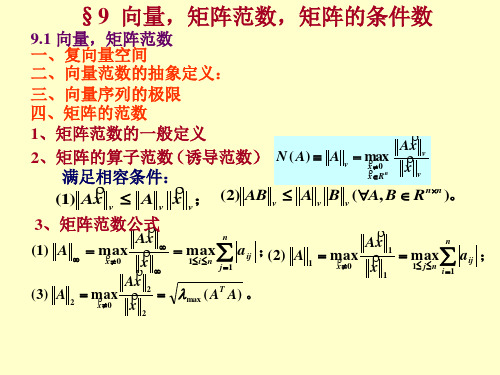
r r 1) 常向量 b 的扰动 δ b 引起解的误差 δ x r r r r r r r r r −1 + 设 A x = b , A ∃ , x是精确解。 A y = b r δ b 的解记为 y = x + δ x 。 r 是精确解。 r r r r r r 即 A( xr+ δ x ) = b + δ b ⇒ Ax + Aδ x = b + δ b, r r r r r −1 ) 由Ax = b ,得 A(δ xr = δ b,即δ x = A (δ b ), r ( 9 .2 ) ⇒ || δ x ||≤ || A−1 || || δ b ||, r 1 || A || r r 即 r ≤ r , ( 9 .3 ) 又 || b ||=|| Ax ||≤|| A || || x || , r || x || r || b || || δb || x 由(9.2)式及(9.3)式得 || δv || ≤|| A −1 || || A || r )式及( ) || b || || x || 结论: 扰动对解的影响 扰动对解的影响。 结论:b扰动对解的影响。 r r n× n 为精确解, 定理27 (1) A ∈ R 为非奇异矩阵,x为精确解, x = b ≠ 0。 定理 r 为非奇异矩阵, 为精确解 A r r r ( 2)设 A( x + δ x ) = br+ δ b ,则b微小误差 扰动、摄动 引起解 的相 微小误差(扰动 引起解x的相 微小误差 扰动、摄动)引起解 r || δx || || δb || ≤|| A −1 || || A || r . v 对误差有估计式 对误差有估计式: || x || || b || 上式说明,常数项b微小误差引起解的相对误差可能是 说明: 上式说明,常数项 微小误差引起解的相对误差可能是 r 说明: || δb || r 的 || A−1 || || A || 倍。 即上式的不等号中的等号可以成立。 即上式的不等号中的等号可以成立。 || b ||
向量和矩阵范数及其应用

2011级计算机实验班
矩阵分析-D.YE
有限维向量空间中的范数(更一般的长度度量)
满足以下性质的函数|| x ||称为x 的范数:
1. 非负性 x 0,当且仅当x 时取等号 2. 齐次性 x x ; 3. 三角不等式 x y x y .
特征方程为
det( I AT A)
可得AT A的特征值为
2
0 1
0 9 1
2
0
1 9.1428, 2 2.9211, 3 0.9361
max ( AT A) 9.1428
矩阵分析-D.YE
A1 5
T A 2 max ( A A)
A 4
2
max ( AT A)
称A的2 范数
其中max ( AT A )为AT A的特征值的绝对值的最 大值
矩阵分析-D.YE
n n 2 A F aij i 1 j Ax 2 A 2 x
2
1
2
A 2 max ( AT A) A F
2
AF x
2 ( || x || 2 || y || 2 )
i.e., || x y || 2 || x || 2 || y || 2
矩阵分析-D.YE
1-范数:
x 1 | xi |
i 1
n
x y 1 | xi yi |
i 1
n
(| xi | | yi |)
矩阵分析-D.YE
矩阵的算子(诱导)范数:
N ( A) A v max
x0 xR n
Ax x
v
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 矩阵范数理论及其应用知识要点:1、向量范数及其性质(范数与赋范空间,n 维向量的1-范数1x 、2-范数2x 、p -范数px 和∞范数x∞,pp lim xx ∞→∞=,aP a xPx =,2H H PxPx x P Px ==,有限维赋范空间的范数是等价的)2、矩阵范数及其相容性(Frobenius 范数,FEn =,相容性:AB A B ≤,1E ≥)3、算子范数(定义,列范数,行范数,谱范数)4、矩阵范数的应用(矩阵序列及幂级数的收敛性,矩阵条件数,摄动理论、矩阵的谱半径)§4.1 向量范数及其性质一、范数与赋范线性空间定义1:如果线性空间V 中的任一向量x ,都对应—个实值函数()f x (记为x ),并满足以下三个条件(称为范数公理):(1)非负性:0x ≠时, x >0;0x =时, x =0。
(2)齐次性:ax =a x ,a K ∈,x V ∈。
(3)三角不等式:x y +≤x +y ,,x y V ∈。
则称x 为V 上向量x 的范数(norm ),V 称为赋范线性空间(normed linear space )。
易证x y -满足距离公理,称之为x 与y 的范数诱导的距离。
若0n x x -→,则称nx 收敛于x ,记为n x x →。
例1:对于连续函数空间[,]C a b 中的向量()f x ,可如下定义范数为:1()()baf t f t dt =⎰,()max ()a t bf t f t ∞≤≤=,1()()bpppa f t f t dt ⎡⎤=⎢⎥⎣⎦⎰,1p ≤<∞。
分别称之为1-范数,∞-范数,p -范数。
注:需要用到数学专业的一些函数不等式,才能证明上述范数的正确性。
性质1:对于赋范线性空间V 上任意的x ,定义实函数()f x x =,则()f x 为V 上的连续函数,即0x x →时,0()()f x f x →,其中0x V ∈。
证明:由000()()f x f x x x x x -=-≤-可知,0x x →时,0()()f x f x →。
因此,()f x 为V 上的连续函数。
性质2:设P 为n 阶可逆矩阵,对于n 维向量n x C ∈,1x 为n C 中的一个范数,令21x Px =,则2x 也为n C 中x 的范数。
证明:(1)非负性:0x ≠时,0Px ≠,210x Px =>;0x =时, 2100x ==。
(2)齐次性:2112()axa Px a Px a x ===,a K ∈,x V ∈。
(3)三角不等式:211122x yPx Py Px Py x y +=+≤+=+,,x y V ∈。
因此,2x 为nC 中x 的范数。
注:内积空间是赋范线性空间,但赋范线性空间不一定构成内积空间。
二、n 维向量的p -范数(1)p ≤≤∞定义2:对于n 维向量12(,,,)T n n x C ξξξ=∈,11ni i x ξ==∑,称为x 的1-范数,记为1x ,由此诱导出的距离称为街区距离。
12221()ni i x ξ==∑,称为x 的2-范数,记为2x ,由此诱导出的距离称为欧氏距离。
1i i nxmax ξ∞≤≤=,称为x 的∞-范数,记为x ∞,由此诱导出的距离称为棋盘距离(也称契比雪夫距离)。
11()npp i pi xξ==∑,称为x 的p -范数,记为p x 。
2H H PxPx x P Px ==,称之为加权范数或椭圆范数,其中P 为可逆矩阵。
定理1:对于n 维向量nx C ∈,pp lim xx ∞→∞=。
注:几何意义上,向量PQ 的2-范数、 ∞-范数和1-范数分别是斜边PQ 长度、直角边PR 长度以及两直角边PR 和RQ 的长度之和。
三、范数的等价性定义3:对任意x V ∈,满足不等式12C xxC x βαβ≤≤的两种范数称为是等价的。
定理2:对于n 维向量nx C ∈,总成立着212xx n x ≤≤,2x x n x ∞∞≤≤,1xx n x ∞∞≤≤,ppxxn x ∞∞≤≤。
定理3:设12,,,n ααα是n 维赋范线性空间E 的一组基,则存在正数,A B ,使得对一切1nk k k x E ξα==∈∑,成立着1221nk k A x B x ξ=⎛⎫≤≤ ⎪⎝⎭∑。
证明:10nk k k x ξα==≠∑时,令21nkk xy ξ==∑,12(,,,)n f y ξξξ=,则12(,,,)n f ξξξ是有界闭集超球面211nk k ξ==∑上连续函数,从而必能取到最小值m 和最大值M ,且显然0m >。
取11,A B M m==,即可证得定理的结论。
结论1:有限维赋范空间的范数是等价的,即对于n 维赋范线性空间E 中的范数a b x x ,,存在正数,A B ,使得对一切x E ∈,成立着ab a A xx B x ≤≤。
推论:范数a b x x ,等价时,0n an lim x →∞=等价于0nbn lim x →∞=。
注:在nC 中,各种p -范数均是等价的,从而对于不同的问题可灵活选用适当的范数。
结论2:n 维赋范线性空间必与n 维向量空间nP 同构并且同胚。
设12,,,n ααα是n 维赋范线性空间E 的一组基,对任何1nk k k x E ξα==∈∑,令()12,,,n Tx ξξξ=,则T 为E 到n P 上的同构映射,并且由A x Tx B x ≤≤可知,T 与1T -均为连续映射,从而E 与n P 是同胚的。
结论3:n 维向量序列{}12(,,,)k kk T n k n x C ξξξ=∈收敛于向量12(,,,)T n n x C ξξξ=∈的充分必要条件为,1,2,,ki i k lim i n ξξ→∞==,即按坐标收敛。
§4.2 矩阵范数及其相容性一、常见的矩阵范数定义1:设n nA C ⨯∈,称11222,1[()]()nHij i j tr A A a ==∑为A 的Frobenius 范数或F -范数,记为FA。
性质1:FA 满足范数公理构成n nC ⨯中范数,并且1FEn =≥。
定理(F -范数的酉不变性):设n nA C ⨯∈中范数,且,n nP Q C⨯∈都是酉矩阵,则FFF PAAQA ==,即给A 左乘或右乘以酉矩阵后其F值不变(在n nA R ⨯∈时P 和Q 都是正交矩阵)。
证明:1122[()][()]H HHFF PAtr A P PA tr A A A ===。
由11222,1()[()]nH Hij FFi j A a tr AA A ====∑及H Q 也为酉矩阵可得,()HH HHFF FF FAQAQ Q A A A ====。
推论:酉(或正交)相似变换下矩阵的F -范数保持不变。
定义2:设n nA C ⨯∈,称1,1nijM i j Aa==∑为1M -范数,1,ij M i j n An max a ∞≤≤=为M ∞-范数。
性质2:1,M M AA∞满足范数公理构成n n C ⨯中范数,并且11M E n =≥,1M En ∞=≥。
二、矩阵范数的相容性定义3:满足条件AB A B ≤的矩阵范数称为具有相容性。
注:工程应用中的矩阵范数常要求满足非负性、齐次性、三角不等式和相容性,因此下文中矩阵范数总假定具有相容性。
性质3:满足相容性的矩阵范数必有1E ≥。
性质4:若A 可逆,则11A A -≥。
例1:Frobenius 范数FA 具有相容性。
例2:1M -范数1M A和M ∞-范数M A ∞具有相容性,但范数1,ij i j nA max a ≤≤=不具有相容性。
三、矩阵范数与向量范数的相容性定义4:若VMV Ax Ax ≤,则称矩阵范数M A 与向量范数V x 具有相容性。
注1:0Vx→时,0V Ax →,即V Ax 是x 的连续函数或Ax 是V 上线性连续算子。
注2:当0x ≠时,()V MVVVAx xA Ax x =≤,从而0V Mx VAx maxAx ≠≤。
例3:22FAxAx ≤。
注:视矩阵为线性变换时,通常要求线性变换是连续即有界的,因此自然有了相容性(包括范数的相容性)要求。
§4.3 矩阵的算子范数一、算子范数的概念定义:0V T x VAx A maxx ≠=。
注:一般算子范数的求解步骤:1、VV AxK x ≤;2、0=1Vx ,0=VAx K 。
二、算子范数的性质性质1:VT V Ax A x ≤。
性质2:TT T ABA B ≤。
性质3:1V T VM x A max Ax A ==≤(假设M A 与V x 具有相容性)。
性质4:1TE=。
三、常见的算子范数1、列范数:11nii x a==∑,111nijj ni A maxa≤≤==∑。
设()n nij A a C⨯=∈,12(,,,)T n n x C ξξξ=∈,令12(,,,)T n Ax y ηηη==,其中1ni i j j j a ηξ==∑,1,2,,i n =。
1111111()n n n n ni ij j ij j i i j i j Ax y a a ηξξ========≤∑∑∑∑∑1111111()()n n nnnij j jijij j nj i j i i a ax max a ξξ≤≤=======≤∑∑∑∑∑。
令11nijj ni M maxa≤≤==∑,则11Ax M x ≤,从而1A M ≤。
不妨设01nij i M a==∑,01j n ≤≤。
取00(0,,0,1,0,,0)j T x =,则011x =,并且0011nij i Ax a M ===∑,因而1A M ≥。
由此可得,111nij j ni A max a ≤≤==∑。
2、行范数:{}1i i nxmax a ∞≤≤=,11nij i nj A max a ∞≤≤==∑。
设()n nij A a C⨯=∈,12(,,,)T n n x C ξξξ=∈,令12(,,,)T n Ax y ηηη==,其中1ni i j j j a ηξ==∑,1,2,,i n =。
1111111()n n ni ij j ij j ij i ni ni ni nj j j Axymax max a max a x max a ηξξ∞∞∞≤≤≤≤≤≤≤≤======≤≤∑∑∑。
令11niji nj M maxa≤≤==∑,则AxM x ∞∞≤,从而AM ∞≤。
不妨设010ni jj M a==>∑,01i n ≤≤。
取000012(,,,)Ti i i n x signa signa signa =,则1x ∞=,并且0000111nnij i j i ji j i nj j Ax max a signa asigna M ∞≤≤===≥=∑∑,因而AM ∞≥。
