九年级数学--《角平分线》教案(1)
最新版初中数学教案《三角形的高、中线与角平分线》精品教案(2022年创作)

三角形的高、中线与角平分线【知识与技能】1.掌握三角形的高、中线与角平分线定义.2.会画三角形的高、中线与角平分线.3.掌握三角形的三条高线、三条中线与三条角平分线的有关性质.【过程与方法】对学生进行操作训练,边训练边讲解,然后学以致用.【情感态度】训练同学们动手操作的能力,提高学习兴趣.【教学重点】画三角形的高线、中线与角平分线.【教学难点】画钝角三角形的高线.一、情境导入,初步认识问题1 如图,△ABC,画它的三条高.问题2 如图,△ABC,画它的三条中线.问题3如图,△ABC,画它的三条角平分线.【教学说明】对问题1,对于钝角三角形的作高要给予集体指导、分类指导,甚至要进行个别指导,以便让绝大局部同学过关.教师讲课前,先让学生完成“自主预习〞.二、思考探究,获取新知思考 1.锐角三角形的三条高、直角三角形的三条高、钝角三角形的三条高的位置有何不同之处?2.三角形的三条高、三条中线、三条角平分线各自有怎样的位置关系?3.三角形的角平分线与角的平分线有什么区别和联系?【归纳结论】1.定义:三角形的高:从三角形的一个顶点向对边所在的直线作垂线,所得的垂线段叫做三角形的一条高.三角形的中线:连接三角形的一个顶点和它对边中点的线段叫做三角形的一条中线.三角形的角平分线:三角形一个角的平分线与对边相交;以这个顶点和交点为端点的线段叫做三角形的角平分线.2.三角形的三条高所在的直线交于一点,这一点有时在形内,有时在直角顶点上,有时在形外;三角形的三条中线交于一点;三角形的三条角平分线交于一点.3.三角形的角平分线与角的平分线的区别是:三角形的角平分线是线段,而角的平分线是一条射线;它们的联系是都是平分角.三、运用新知,深化理解1.如图,AD 是△ABC 的中线;BE 是△ABC 的角平分线,CF 是△ABC 的高,填空:〔1〕BD= =21 ; 〔2〕∠ABE=∠ =21∠ ; 〔3〕∠ =∠ =90°.2.如图,△ABC 中,∠A 是钝角.〔1〕画出AC 、AB 上的高BD 、CE ;〔2〕画出∠ABC 的平分线BF ;〔3〕画出边AB 上的中线CG.3.,如图,AB ⊥BD 于B ,AC ⊥CD 于C ,且AC 与BD 交于点E.那么〔1〕△ADE的边DE 上的高为,边AE 上的高为 ;〔2〕假设AE=5,DE=2,CD=59,那么AB= .4.如下列图,等腰△ABC 中,AB=AC ,一腰上的中线BD 将这个等腰三角形的周长分成15和6两局部,求这个三角形的腰长及底边长.“三角形的高、中线与角平分线〞后,我们知道“三角形的一条中线将原三角形分成两种相等的两局部〞.课后余老师给同学们布置了这样一道思考题:有一块三角形的厚薄均匀的蛋糕,要平均分给6个小朋友,要求只切3刀,请你在图中把你的方案画出来,并说明理由.【教学说明】题1、2、3可让学生自主完成,题4、5教师可给予相应的指导当三角形两条高求其他边长或一高与其他边长求另一高时,常用面积作为中间量.涉及等腰三角形边的问题时,常要分情况讨论,然后看它们是否满足三边关系,不满足的要舍去.【答案】1.〔1〕DCBC〔2〕CBE ABC〔3〕CFA CFB2.图略. DC 29 解析:△△ADE=21DE ·AB=21AE ·DC ,即21×2×AB=21×5×95,AB=29. 4.解:设AB=AC=2x,那么AD=CD=x.(1)当AB+AD=15,BC+CD=6时,有2x+x=15,所以x=5,2x=10,BC=6-5=1.(2)当BC+CD=15,AB+AD=6时,有2x+x=6.所以x=2,2x=4,所以BC=13. 因为4+4<13,故不能组成三角形.所以三角形的腰长为10,底边长为1.5.略.四、师生互动,课堂小结三角形的高、中线与角平分线的定义与性质.请假设干名学生口述小结,老师再利用电子课件将小结放映在屏幕上.1.布置作业:从教材“习题”中选取.2.完成练习册中本课时的练习.本课时教学以“自主探究——合作交流〞为主体形式,先给学生独立思考的时间,提供学生创新的空间与可能,再给不同层次的学生提供一个交流合作的时机,培养学生独立探究,合作学习的能力。
2022人教版数学《角平分线的判定》配套教案(精选)

第2课时 角平分线的判定1.掌握角平分线的判定定理.(重点)2.会用角平分线的判定定理解决简单的实际问题.(难点)一、情境导入中新网和田2015年2月25日电,新疆考古团队近日在斯皮尔古城及周边发现迄今为止最早的园林之城.如图,某考古队为进行研究,寻找一座古城遗址.根据资料记载,该城在森林附近,到两条河岸的距离相等,到古塔的距离是3000m.根据这些资料,考古队很快找到了这座古城的遗址.你能运用学过的知识在图中合理地标出古城遗址的位置吗?请你试一试.(比例尺为1∶100000)二、合作探究探究点一:角平分线的判定定理 【类型一】 角平分线的判定如图,BE =CF ,DE ⊥AB 的延长线于点E ,DF ⊥AC 于点F ,且DB =DC ,求证:AD 是∠BAC 的平分线.解析:先判定Rt △BDE 和Rt △CDF 全等,得出DE =DF ,再由角平分线的判定可知AD 是∠BAC 的平分线.证明:∵DE ⊥AB 的延长线于点E ,DF ⊥AC 于点F ,∴∠BED =∠CFD ,∴△BDE 与△CDF是直角三角形.在Rt △BDE 和Rt △CDF 中,∵⎩⎪⎨⎪⎧BE =CF ,BD =CD ,∴Rt △BDE ≌Rt △CDF ,∴DE =DF ,∴AD 是∠BAC 的平分线.方法总结:证明一条射线是角平分线的方法有两种:一是利用三角形全等证明两角相等;二是角的内部到角两边距离相等的点在角平分线上.【类型二】 角平分线性质和判定的综合如图所示,△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,下面给出四个结论,①AD平分∠EDF;②AE=AF;③AD上的点到B、C两点的距离相等;④到AE、AF距离相等的点,到DE、DF的距离也相等.其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个解析:由AD平分∠BAC,DE⊥AB,DF⊥AC可得DE=DF,由此易得△ADE≌△ADF,故∠ADE =∠ADF,即①AD平分∠EDF正确;②AE=AF正确;角平分线上的点到角的两边的距离相等,故③正确;∴④到AE、AF距离相等的点,到DE、DF的距离也相等正确;①②③④都正确.故选D.方法总结:运用角平分线的性质或判定时,可以省去证明三角形全等的过程,可以直接得到线段或角相等.【类型三】添加辅助线解决角平分线的问题如图,已知:△ABC的∠ABC和∠ACB的外角平分线交于点D.求证:AD是∠BAC的平分线.解析:分别过点D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,然后利用角平分线上的点到角两边的距离相等可知DE=DG,再利用到角两边距离相等的点在角平分线上证明.证明:分别过D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,∵BD平分∠CBE,DE⊥BE,DF⊥BC,∴DE=DF.同理DG=DF,∴DE=DG,∴点D在∠EAG的平分线上,∴AD是∠BAC的平分线.方法总结:在遇到角平分线的问题时,往往过角平分线上的一点作角两边的垂线段,利用角平分线的判定或性质解决问题.探究点二:三角形的内角平分线【类型一】利用角平分线的判定求角的度数在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )A.110°B.120°C.130°D.140°解析:由已知,O 到三角形三边的距离相等,所以O 是内心,即三条角平分线的交点,AO ,BO ,CO 都是角平分线,所以有∠CBO =∠ABO =12∠ABC ,∠BCO =∠ACO =12∠ACB ,∠ABC +∠ACB=180°-40°=140°,∠OBC +∠OCB =70°,∠BOC =180°-70°=110°,故选A.方法总结:由已知,O 到三角形三边的距离相等,得O 是内心,再利用三角形内角和定理即可求出∠BOC 的度数.【类型二】 三角形内角平分线的应用已知:如图,直线l 1,l 2,l 3表示三条相互交叉的公路,现要建一个塔台,若要求它到三条公路的距离都相等,试问:(1)可选择的地点有几处? (2)你能画出塔台的位置吗?解析:(1)根据角平分线的性质得出符合条件的点有4处.(2)作出相交组成的角的平分线,平分线的交点就是所求的点.解:(1)可选择的地点有4处,如图:P 1、P 2、P 3、P 4,共4处.(2)能,如图,根据角平分线的性质的作三条直线相交的角的平分线,平分线的交点就是所求的点.方法总结:三角形内角平分线的交点到三角形三边的距离相等,反过来,到三角形三边距离相等的点,即为三角形内角平分线的交点,这一结论在以后的学习中经常遇到.三、板书设计1.角平分线的判定定理.2.三角形三条内角平分线相交于一点,这点到三角形三边的距离相等.本节课借助于直观的模型引导学生进行观察、猜想和验证,从而引导学生在自主探究的基础上,通过与他人的合作交流探究出角平分线的性质定理和逆定理,这样有效地提高了课堂的教学效果,促进了学生对新知识的理解和掌握.不足之处是少数学生在应用角平分线的性质定理和逆定理解题时,容易忽视“角平分线上的点到角两边的距离相等”这一条件,需要在今后的教学和作业中加强巩固和训练.角的平分线的性质(一)教学目标(一)教学知识点角平分线的画法、角平分线的性质1. (二)能力训练要求1.掌握角平分线的性质1 2.会用尺规作一个已知角的平分线. (三)情感与价值观要求在利用尺规作图的过程中,培养学生动手操作能力与探索精神. 教学重点利用尺规作已知角的平分线.角平分线的性质1.教学难点角的平分线的性质1 教学方法引导发现、讲练结合法. 教具准备多媒体课件 教学过程一.提出问题,创设情境问题:图中哪条线段的长可以表示点P 到直线l 的距离 ? 导入新课,明确学习目标如果老师手里只有直尺和圆规,你能帮忙设计一个作角的平分线的操作方案吗?二.合作交流 探究新知 探究1想一想:下图是一个平分角的仪器,其中AB=AD ,BC=DC .将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE ,AE 就是角平分线.你能说明它的道理吗? 教师活动:播放多媒体课件,演示角平分仪器的操作过程,使学生直观了解得到射线AC 的方法. 学生活动:观看多媒体课件,讨论操作原理.[生1]要说明AC 是∠DAC 的平分线,其实就是证明∠CAD=∠CAB .[生2]∠CAD 和∠CAB 分别在△CAD 和△CAB 中,那么证明这两个三角形全等就可以了.[生3]我们看看条件够不够.AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩所以△ABC ≌△ADC (SSS ). 所以∠CAD=∠CAB .即射线AC 就是∠DAB 的平分线.[生4]原来用三角形全等,就可以解决角相等.线段相等的一些问题.看来温故是可以知新的.试一试:老师再提出问题:通过上述探究,能否总结出尺规作已知角的平分线的一般方法.自己动手做做看.然后与同伴交流操作心得.(分小组完成这项活动,教师可参与到学生活动中,及时发现问题,给予启发和指导,使讲评更具有针对性)讨论结果展示:作已知角的平分线的方法:已知:∠AOB.求作:∠AOB的平分线.作法:(1)以O为圆心,适当长为半径作弧,分别交OA、OB于M、N.(2)分别以M、N为圆心,大于12MN的长为半径作弧.两弧在∠AOB内部交于点C.(3)作射线OC,射线OC即为所求.(教师根据学生的叙述,作多媒体课件演示,使学生能更直观地理解画法,提高学习数学的兴趣).点拨:1.在上面作法的第二步中,去掉“大于12MN的长”这个条件行吗?2.第二步中所作的两弧交点一定在∠AOB的内部吗?(设计这两个问题的目的在于加深对角的平分线的作法的理解,培养数学严密性的良好学习习惯)学生讨论结果总结:1.去掉“大于12MN的长”这个条件,所作的两弧可能没有交点,所以就找不到角的平分线.2.若分别以M、N为圆心,大于12MN的长为半径画两弧,两弧的交点可能在∠AOB•的内部,也可能在∠AOB的外部,而我们要找的是∠AOB内部的交点,•否则两弧交点与顶点连线得到的射线就不是∠AOB的平分线了.3.角的平分线是一条射线.它不是线段,也不是直线,•所以第二步中的两个限制缺一不可.4.这种作法的可行性可以通过全等三角形来证明.探究2:做一做1[师]请同学们拿出准备好的折纸与剪刀,自己动手,剪一个角,把剪好的角对折,使角的两边叠合在一起,再把纸片展开,你看到了什么?把对折的纸片再任意折一次,然后把纸片展开,又看到了什么?[生]我发现第一次对折后的折痕是这个角的平分线;再折一次,又会出现两条折痕,而且这两条折痕是等长的.这种方法可以做无数次,所以这种等长的折痕可以折出无数对. [师]你的叙述太精彩了.这说明角的平分线除了有平分角的性质,还有其他性质,今天我们就来研究这个问题.做一做2角平分线的性质即已知角的平分线,能推出什么样的结论.操作:1.折出如图所示的折痕PD、PE.2.你与同伴用三角板检测你们所折的折痕是否符合图示要求.画一画:按照折纸的顺序画出一个角的三条折痕,并度量所画PD、PE是否等长?拿出两名同学的画图,请大家评一评,以达明确概念的目的.[生]同学乙的画法是正确的.同学甲画的是过角平分线上一点画角平分线的垂线,而不是过角平分线上一点画两边的垂线段,所以同学甲的画法不符合要求.[生甲]噢,对,我知道了.[师]同学甲,你再做一遍加深一下印象.教师提出问题:你能叙述所画图形的性质吗?生回答后,教师进一步引导:观察操作得到的结论有时并不可靠,你能否用推理的方法验证你的结论呢?证一证:引导学生证明角平分线的性质 1,分清题设、结论,将文字变成符号并加以证明(一生板演)说一说: 引导学生结合图形从文字和符号的角度分别叙述问题1:你能用文字语言叙述所画图形的性质吗?[生]角平分线上的点到角的两边的距离相等.问题2:(出示)能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.学生通过讨论作出下列概括:∵ OC平分∠AOB,PD⊥OA,PE⊥OB,∴PD=PE.于是我们得角的平分线的性质:在角的平分线上的点到角的两边的距离相等.三、用一用:1、如图,△ABC的角平分线BM、CN相交于点P.此例放到第二课时讲求证:点P到三边AB、BC、CA的距离相等.[师生共析]点P到AB、BC、CA的垂线段PD、PE、PF的长就是P点到三边的距离,•也就是说要证:PD=PE=PF.而BM、CN分别是∠B、∠C的平分线,•根据角平分线性质和等式的传递性可以解决这个问题.证明:过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足为D、E、F.因为BM是△ABC的角平分线,点P在BM上.所以PD=PE.同理PE=PF.所以PD=PE=PF.即点P到三边AB、BC、CA的距离相等.巩固所学及时点拨四.丰收乐园学生充分交流、各抒己见教后反思:本节知识的应用主要存在以下问题:1、对距离把握不到位,点到直线的垂线段长才叫距离2、不会直接使用角平分线的性质,而是使用全等将性质再证一3、采用角平分线性质解题强调三个条件。
北师大版数学九年级上册1.4《角平分线》教学设计1

北师大版数学九年级上册1.4《角平分线》教学设计1一. 教材分析《角平分线》是北师大版数学九年级上册第1章“几何图形变换”中的一个知识点。
本节课主要介绍了角平分线的概念、性质及运用。
教材通过引入角平分线来让学生进一步理解角的性质,培养学生的几何思维能力。
二. 学情分析学生在学习本节课之前,已经掌握了直线、射线、线段等基本几何概念,并了解了垂线的性质。
在此基础上,学生需要进一步理解角平分线的概念,并能够运用角平分线解决实际问题。
三. 教学目标1.知识与技能目标:让学生掌握角平分线的概念、性质和运用。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生的几何思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作精神。
四. 教学重难点1.重点:角平分线的概念、性质和运用。
2.难点:角平分线的证明和运用。
五. 教学方法1.引导发现法:教师引导学生观察、操作、思考,发现角平分线的性质。
2.合作学习法:学生分组讨论,共同解决问题。
3.实践操作法:学生动手操作,加深对角平分线性质的理解。
六. 教学准备1.教具:三角板、直尺、圆规等。
2.学具:学生每人一份三角板、直尺、圆规等。
七. 教学过程1.导入(5分钟)教师通过提问方式引导学生回顾直线、射线、线段的性质,为新课的学习做好铺垫。
2.呈现(10分钟)教师通过展示三角板,引导学生观察角平分线的定义,并用几何画板软件动态展示角平分线的性质。
3.操练(10分钟)学生分组讨论,利用三角板、直尺、圆规等工具,自行探索角平分线的性质。
教师巡回指导,解答学生疑问。
4.巩固(10分钟)教师选取几组学生得出的结论,让学生进行分析、判断、验证。
学生通过互相交流,巩固对角平分线性质的理解。
5.拓展(10分钟)教师提出一些实际问题,让学生运用角平分线的性质进行解决。
例如:在平面直角坐标系中,如何找到一点,使得该点到两点的距离相等?6.小结(5分钟)教师引导学生总结本节课所学内容,巩固角平分线的性质及运用。
角平分线(1)

九年级数学组 8月31日
学习目标:
通过学习角平分线定理及逆 定理的过程,掌握该定理及逆定 理,并运用之进行证明、计算、 作图,以及掌握该定理在三角形 中的应用
自学指导
1.任意作一个角,利用尺规作出它的角平 分线。
2.在角平分线上任取一点,过这一点作角 两边的垂线,这两条垂线段有什么关系?
间有两家工厂A、B,现在要修一个货物
中转站,使它到两条公路的距离相等,
以及到两个工厂距离相等,你能帮助确
定中转站的地址吗?请试试。
中考真题:
如图,梯形ABCD,ABCD,AD=DC=CB, AD、BC的延长线相交于G,CE⊥AG于E, CF⊥AB于F,
(1)请写出图中4组相等的线段Байду номын сангаас已知的相等线 段除外)
求证:OC是∠AOB的角平分线 A
D
C
O
P
E B
定理:在一个角的内部,且到角的两边距离相等的点, 在这个角的平分线上。
6.线段垂直平分线与角平分线的区别 与联系:
(1)都有“平分、距离相等”的特点.
(2)线段的垂直平分线是一条直线;角平 分线是一条射线.
(3)三角形三边的垂直平分线的交点到 三角形三个顶点的距离相等,三角形角 平分线的交点到三边的距离相等.
自学检测
1、在△ABC中∠C=90°,∠A的平分线交BC于D,BC=CM, BD:DC:=4:3,则点D到AB的距离为__。
2、在RT△ABC中,∠C=90°,BD平分∠ABC交AC于D, DE是斜边AB的垂直平分线,且DE=1CM,则AC=______.
3、∠AOB的平分线上一点M,M到OA的距离为2CM,则M 到OB的距离为____________。
九年级数学画角平分线(教学课件201908)

O
B
D
; AG:/
;
而跄鸾斯应者也 非忠则正 并有名 王公设险以守其国 以叙其欢心 故刘氏之伐 黄尘为之四合兮 古人所慎 恐死亡之不暇 万姓赖之 明主察焉 至于丹楹刻桷 而损益不同 然则动者 丑名彰闻 贼未至三十步 共相匡矫 愚也 及入而抵 虽幽贱负俗 燕喜 又留不遣 陆浑 曲盖 得其人不可臣而 畜 赵胤领其父馀兵属左甄 玄纁之贽 凉州遂平 圣恩广厚 峻平 其心必异 此非仆所能也 今日受诛 而置郡县更多 如在州郡 皙曰 果破贼 祖蕤 振乃徙太子于小坊中 南单于复来降附 使起兵讨赵王伦 赵郡太守 自非主臣尚德兼爱 段灼 朝野称允 玘三定江南 人皆感化 中书监 责辅之无所 举荐 又服寒食药 韵清绕梁 蜀小吴大 宗族称孝 聆鸣蜩之号节兮 }转佐著作郎 而天下之谷可以无乏矣 无忧不平也 朝廷不从 欲醇醇而任德 阎缵向雄 祖略 同种土崩 不忘退而已 帝寻悟而恨焉 惟追昔以怀今兮 相下无餍 陛下不以臣不才 岂若托身权戚 机曰 历光禄勋 永言启沃 故其 诗曰 可堪扶舆 闻者皆嗟味之 纳谟士之算 为涿令 协之乱政 太夫人在堂 外无微介 好谋善断 令匈奴远迹 夫人之性陵上 必有颠仆 去年十二月 凡厥庶事 尼以为王者膺受命之期 陆公喻之长蛇 使君臣释然 有与共亡 王尊等付廷尉 祸福舛错 访少沈毅 为公府掾 阴阳否泰 侍臣多得罪 闻 之者叹息 想众人见明也 乃使于官舍设灵坐 不得不保小以固存 早终 宫臣毕从 哀二亲早亡陨 任得其正 帝从之 养志不仕 犹树艺之有丰壤 苟非周材 自分败没 段颎临冲 骖飞黄 故专施中丞 孰不失望 然城狐社鼠也 酒驾方轩 岂非事势使之然欤 初 琅邪王戎 夫称君子者 乃延台保 若人 有所患苦者 为所驱驰 共推吴兴太守顾秘都督扬州九郡军事 载性闲雅 疏斥正士 诸有疾病满百日不差 故据上品者 计日听其败耳 吾亦怪子较论而不折中也 劲利之器易用也 昔
角的平分线数学教案

角的平分线数学教案
标题:《探索角的平分线》
一、教学目标
1. 知识与技能目标:理解并掌握角的平分线的概念,能够熟练地运用尺规作图法作出任意角的平分线。
2. 过程与方法目标:通过观察、思考、实践,提高学生的空间观念和逻辑思维能力。
3. 情感态度价值观目标:培养学生对几何学习的兴趣,增强他们解决问题的信心。
二、教学重点和难点
重点:理解和掌握角的平分线的概念,掌握尺规作图法作出任意角的平分线的方法。
难点:理解和应用角的平分线的性质。
三、教学过程
1. 导入新课:通过实例引入角的平分线的概念,引发学生的好奇心和求知欲。
2. 新课讲授:
(1) 角的平分线的概念:讲解角的平分线的定义,并让学生自己画出一些角的平分线,加深理解。
(2) 尺规作图法:详细解释如何使用尺规作图法作出任意角的平分线,包括步骤和注意事项。
(3) 角的平分线的性质:引导学生通过实验、讨论等方式发现角的平分线的一些性质,如等腰三角形的判定定理等。
3. 巩固练习:设计一些习题,让学生在实践中巩固所学知识。
4. 总结反思:回顾本节课的主要内容,鼓励学生分享他们的学习体验和收获。
四、作业布置
设计一些题目,要求学生在家中完成,以检验他们对角的平分线的理解和掌握程度。
五、教学评价
根据学生在课堂上的表现和作业完成情况,对学生的学习效果进行评估。
六、教学反思
教师应反思自己的教学方法是否有效,是否有需要改进的地方,以便更好地满足学生的学习需求。
河南省郑州市侯寨二中九年级数学上册《角平分线1》课件 人教新课标版

例1: 实际问题
数学化 C
P
┒
O
数学问题源于生活实践,反过来数学又为生活实践服务
例2: 已知:如图,E是∠BAC平分 线上的一点,EB⊥AB,EC⊥AC,B, C分别是垂足。你能得到哪些结论
例3: 已知:如图所示:PA,PC分别
是⊿ABC外角∠MAC与∠NCA平分线,
它们交于P,PD⊥BM于M,
PF⊥BN于F。 求证: 点P在
M D
∠MBN的平分线上. A
P
E
B
C FN
活动与探究:已知:如图, 方法总结:(1) ∠1=∠2,P为BN上一点,且 有角的平分线(或 PD⊥BC于D,AB+BC=2BD 证明是角的平分线)
求证:∠BAP+∠BCP=180° 时,过角平分线上 的点向两边作垂线
定理2 到一个角的两边的距 逆定理 和一条线段两个端点距
离相等的点,在这个角的平分 离相等的点,在这条线段的垂
线上。
直平分线上。
角的平分线是到角的两边 线段的垂直平分线可以看作是和
距离相等的所有点的集合 线段两上端点距离相等的所有点
的集合
点的集合是一条射线
点的集合是一条直线
作业(必做题):课本:习题,配套练习
A
.. D C
B
问题探讨:
3、已知:如图所示,∆ABC 中,∠C=2∠B,∠1=∠2,求 证:AB=AC+CD。
B
4、如图所示,在∆ABC中,
A
∠BAC=90º,AB=AC,BE平
分∠ABC,CE⊥BE,
1
求证:CE= 2 BD。
B
A
12
D
C
E D
角平分线(一)
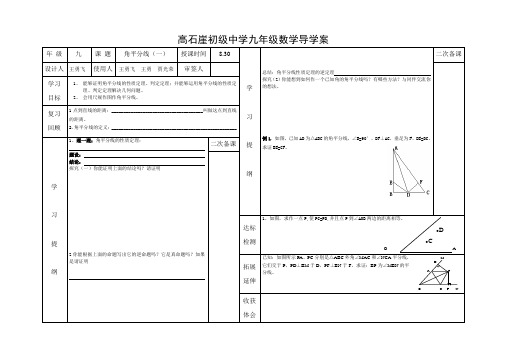
年 级 九 课 题 角平分线(一) 授课时间 审签人 学 8.30
总结:角平分线性质定理的逆定理 探究 (2) 你能想到如何作一个已知角的角平分线吗?有哪些方法?与同伴交流你 的想法。
二次备课
设计人 王勇飞 学习 目标 复习 回顾
使用人 王勇飞 王勇 贾光荣
1、 能够证明角平分线的性质定理、判定定理;并能够运用角平分线的性质定 理、判定定理解决几何问题。 2、 会用尺规作图作角平分线。 1 点到直线的距离:______________________________________叫做这点到直线 的距离。 2.角平分线的定义: ____________________________________________________ 1、理一理:角平分线的性质定理: 题设: 结论: 探究(一)你能证明上面的结论吗?请证明
日期 等级
8.30 8
习
例 1.如图,已知 AD 为△ABC 的角平分线,∠B=90°,DF⊥AC,垂足为 F,DE=DC,
二次备课
提
求证 BE=CF。
纲
学
习 达标 提
2.你能根据上面的命题写出它的逆命题吗?它是真命题吗?如果 是请证明
1、如图,求作一点 P,使 PC=PD,并且点 P 到∠AOB 两边的距离相等。
检测
O 已知:如图所示 PA、PC 分别是△ABC 外角∠MAC 和∠NCA 平分线, 它们交于 P,PD⊥BM 于 D,PF⊥BN 于 F,求证:BP 为∠MBN 的平 分线。
2.已知:如图,∠B=∠C=90 ,DM 平分∠ADC, AM 平分∠DAB 。求证: M B=MC
0
2.如右图,已知 BE⊥AC 于 E,CF⊥AB 于 F,BE、CF 相交于点 D,若 BD=CD. 求证:AD 平分∠BAC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章第四节角平分线教案(2)
教学目标:1、知识目标:(1)掌握角平分线的性质定理和逆定理;
(2)能够运用性质定理和逆定理证明两个角相等或两条线段相等;
(3)能够判定两个命题是否为互逆命题,并能写出一个命题的逆命题.
2、能力目标:(1)通过“判断题”的练习,提高学生的辨析能力;
(2)通过公理的初步应用,培养学生的逻辑推理能力及创新的能力.
3、情感目标:(1)通过自主学习的发展体验获取数学知识的感受;
(2)通过知识的纵横迁移感受数学的辩证特征。
教学重点:角平分线的性质定理,逆定理及它们的应用。
教学难点:a、角平分线定理和逆定理的应用;b、这两个定理的区别;c、写命题的逆命题。
教学用具:直尺,圆规
教学方法:谈话法
教学过程:1、新课引入
分组:分别画直角、锐角、钝角三角形,并画三个角的角平分线。
三条角平分线有几个交点?度量这点到三边的距离,并比较大小
2、定理的获得: 让学生用文字语言叙述出定理的内容
角平分线的性质定理:在角平分线上的点到这个角两边距离相等。
强调说明:(1)、定理的条件及结论的符号表示;
(2)、定理的作用:直接证明两线段相等。
使用的前提是有角的平分线,关键是图中是否有“垂直”。
3、运用逆向思维,导出定理的逆定理
探究活动
如图,公路南有一学校在铁路的东侧,到公路的距离与到铁路的距离相等,并且与两路交叉
处O的距离为400米,在图上标出学校的位置,并说明理由(比例尺1:10000)。
提示:解决这类问题的方法是把实际应用问题转化为数学问题,然后用数学知识解决。
解:把公路、铁路看作两条相交直线,画出它们交角的平分线,在角的平分线上,从顶
点量出表示实际400米长的线段便可确定学校的位置。
表示实际400米长的线段为:0.04
米=4cm
1、判断题
(1)角的平分线上的点到角的两边的距离相等;
(2)三角形两个内角的平分线交点到三边距离相等;
(3)三角形两个内角的平分线的交点到三个顶点的距离相等;
(4)点E、F分别在∠AOB的两边上,P点到E、F两点距离相等,所以P点在∠AOB
的平分线上
(5)若OC是∠AOB的平分线,过OC上的点P作OC的垂线,交OB于D,交OA 于E,则线段PD、PE的长分别是P点到角两边的距离。
3、写出下列定理的逆命题,并判断真假?(1)同位角相等,两直线平行;
(2)如果X=3,那么X2=9;
(3)如果△ABC是直角三角形,那么当△ABC的三个外角中有两个钝角;
逆命题是:如果△ABC的三个外角中只有两个是钝角,那么△ABC是直角三角形;
(4)全等的两个三角形的面积相等。
5、已知:如图,BD是∠ABC的平分线,DE⊥AB于E,
三角形ABC的面积=36平方厘米,AB=18cm,BC=12cm,求DE的长
6、已知:如图3,在△ABC中,∠B=600,△ABC的角平分线
AD、CE线相交于点O。
求证:AE+CD=AC(提示:在AC上截取AF=AE,由条件不难证得CF=CD。
)作业:书P37EX1.9。
