难点突破：立体图形的外接球与内切球问题讲课教案

合集下载

高中数学外接球、内切球教学设计详案

立体几何外接球、内切球问题一、教学分析：纵观近几年高考对于组合体的考查，与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显，要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答•从实际教学来看，这部分知识学生掌握较为薄弱、认识较为模糊，看到就头疼的题目•分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理.从近几年全国高考命题来看，这部分内容以选择题、填空题为主，大题很少见•此部分是重点也是一个难点，建议分两个课时，第一个课时以基础的方法为主，第二个课时在第一课时的基础上进行总结整理并拓展。

二、学情分析：学生在高一必修二教材系统的学习了立体几何，这部分内容本身对知识掌握的要求就比较高，又是难点，再加上疫情原因，很多同学不能系统了解和掌握，而一部分学生也只能解决长方体的外接球问题，稍复杂一点就不会。

三、教学目标：知识与技能：学生学会用构造法解决空间几何体的外接球、内切球问题。

过程与方法：学生建立空间感，体会转化数学思想方法。

情感、态度、价值观：完善学生知识体系，增进学生对数学的信心和兴趣。

四、教学重点：学会转化、数形结合的思想方法。

五、教学难点：构造法的要点。

六、教学过程分析问：如果是正方体，它的体对角线长和棱长什么关系2.复习圆柱的外接球问题问：一个球满足什么条件，我们把它叫做这个圆柱的外接球问：球心的位置在哪问：如果给出圆柱的底面半径和母线长，怎么求它外接球的半径问：一个球满足什么条件，我们把它叫做这个圆锥的外接球问：球心的位置在哪问：如果给出圆锥的底面半径和母线长，怎么求它外接球的半径方程：先算出H其实我们一直是在求它们截面的外接圆的半径，长方体对角面矩形的顶点都在球面上，长方体对角面长方形外接圆的直径也就是这个长方体外接球的直径，圆柱和圆锥我们解是它们轴截面图形外接圆的半径, 把求一个空间几何体外接球半径问题转化为求一个截面图形外接圆半.复习圆锥的外接球问题O径问题的过程这就是我们所说的立体问题平面化三角形的外接圆半径除了刚才同学想到在直角三角形中用勾股定理列方程的方法，还有什么方法回想一下解三角形那一章正弦定理：比较正弦定理，不用确定外接圆的圆心知道么）活动二:问题三棱锥的三条棱PA, PB, PC 两两垂直，PA 1, PB 2, PC 3,则其外接球的半径为问：三棱锥的的顶点和长方体的顶点之间什么关系它们的外接球是不是相同的问：球心在哪，半径怎么求（求长方体体对角线长需要长方体的长宽高，这几个量我们现在解决一个几何体的外接球可能有多种办法，让学生发挥想象，提出各种方法，通过比较生成对结合体外接球问题的认识。

空间几何体的外接球和内切球问题(提高)(最新人教版优质教案)( 含解析 )

进门测1正方体中，若外接圆半径为，则该正方体外接球的表面积为（）A．B．C．D．答案C解答如图所示，为等边三角形，设的外接圆半径为，由正弦定理可得：，，设正方体边长为，则，，设外接球半径为，则，，面积，故选．2已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，，则此球的表面积等于．答案．解答设此球半径为，三棱柱高为，则底面积，，解得，又，，，为直角三角形，的外接圆半径,，球的表面积3在三棱锥中，，，，则三棱锥的外接球的表面积为（）A．B．C．D．答案A解答在中，由余弦定理得，，，，，≌，，，，为等边三角形，，取中点为点，连接、，如图所示，外接球球心必在过点（外接圆圆心），垂直平面的直线上，其中，，，，，，又，，平面，，设外接球半径为，，，，，，，外接球的表面积为，故选．4三棱锥中，平面且，是边长为的等边三角形，则该三棱锥外接球的表面积为（）A．B．C．D．答案C解答第面是边长为的等边三角形，设底面所截外接球的截面圆的半径为，空间几何体的外接球和内切球问题知识点梳理：，，如图所示，，，设外接球半径为，，外接球，故选．5已知三棱锥的体积为，是等腰直角三角形，其斜边，且三棱锥的外接球的球心恰好是的中点，则球的体积为.答案解答设球的半径为，球心到平面的距离为，则由是的中点得，点到平面的距离等于，所以＝＝＝，解得＝，记的中点为，则平面.在中，＝＋，即＝＋＝，所以球的体积＝＝＝.一、外接球常见模型1. 【墙角模型】三条线两个垂直，不找球心的位置即可求出球半径方法：找三条两两垂直的线段，利用公式，即，求出．2. 【对棱相等模型】三棱锥中，已知，，，则可补形为长方体，再求外接球半径．第一步：画出一个长方体，标出互为异面直线的三组面对角线；第二步：设出长方体的长宽高分别为，，列方程组：；第三步：根据墙角模型，，即．3. 【切瓜模型】两个大小圆面互相垂直且交于小圆直径，利用正弦定理解大圆三角形是通法．如图，平面平面，且(即为小圆的直径)，则球心在大圆面上，利用正弦定理即可求出外接球半径．4. 【垂面模型】三棱锥中，当一条棱垂直于某个面时，球心离底面距离为这条棱长的一半．如图平面，求外接球半径的步骤：第一步：将画在小圆面上，为小圆直径的一个端点，作小圆直径，连接，则必过球心；第二步：为的外心，所以平面，算出小圆的半径(可利用正弦定理计算)，又；第三步：利用勾股定理求三棱锥的外接球半径：①；或②．如图，的射影是的外心三棱锥的三条侧棱相等三棱锥的底面在圆锥的底上，顶点也是圆锥的顶点．求解步骤：第一步：确定球心的位置，取的外心，则三点共线；第二步：先算出小圆的半径，再算出棱锥的高(也是圆锥的高)；第三步：勾股定理：，解出．方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径．5. 【汉堡模型】直棱柱的外接球、圆柱的外接球如图，直三棱柱内接于球(同时直棱柱也内接与圆柱，棱柱上下底面可以是任意三角形)．第一步：确定球心的位置，是的外心，则面；第二步：算出小圆半径，(也是圆柱的高)；第三步：勾股定理：，即．6. 【折叠模型】两个全等三角形或等腰三角形拼在一起，或菱形折叠第一步：先画出如图所示的图形，将画在小圆上，找出和的外心和；第二步：过和分别作平面和平面的垂线，两垂线的交点即为球心，连接，；第三步：解，算出，在中，勾股定理：．7. 【直角双拼模型】两直角三角形拼接在一起(斜边相同)题设：，求三棱锥外接球半径（分析：取公共的斜边的中点，连接，，则，为三棱锥外接球球心，然后在中求出半径）．二、内切球1. 正方体的中心与内切球的球心重合，若正方体的棱长为，内切球的半径为，，如下图所示：2. 正四面体的中心与内切球的球心重合，正四面体的棱长为，体高为，内切球半径为，，如下图所示：证明：正四面体的棱长为，体高为，内切球半径为．正四面体的内切球半径为，正四面体的体积，得①，在中，，即，化简得②，由①②可得．3. 空间多面体的每个面的面积为，多面体的体积为，则该多面体的内切球半径为．例如，利用等体积法求四面体的内切球半径．例题精讲：6设长方体的长、宽、高分别为，，，其顶点都在一个球面上，则该球的表面积为（）A ．B ．C ．D ．答案B解答由题意可知，该球为长方体的外接球，则该球的半径，则该球的表面积为，故选．7已知三棱锥的顶点都在球的表面上，若，，两两互相垂直，且，则球的体积为（）A．B ．C ．D ．答案C解答且，，，，取的中心连接，设球心为，球半径为，则，延长交于，则，，，在中，，，在中，，即，解得，，故选．8四面体中，，，点是的中点，点在平面的射影恰好为的中点，则该四面体外接球的表面积为（）A．B．C．D．答案A解答，为等边三角形，又，，为等腰直角三角形，又为中点，为中点，，，点为外接圆圆心，设球心为，则面，在中，，，在中，，，设球半径为，则，又，，即，解得，，外接圆表面积，故选．9三棱锥中，平面，，，，则该三棱锥外接球的表面积为（）A．B．C．D．答案A解答将其放在长方体中如下图所示：则有，，在中，，在中，，则球的半径，表面积，故选．10已知三棱柱的个顶点都在球的球面上，若，，，，则球的半径为（）A．B．C．D．答案C解答由于三棱柱的个顶点都在球上，所以三棱柱是直三棱柱，如图，取中点，中点，连结，，则垂直底面，又，，、分别是两底面三角形外接圆的圆心，故球心在上且是的中点，四边形是平行四边形，，，又，，，，，，，，，，，，故选．11已知三棱锥中，，，则三棱锥的外接球的表面积为．答案．解答由题意知，是对棱相等的三棱锥，则三棱锥的六条棱可以是长方体的面对角线，如下图所示：则的外接球与长方体外接球相同，，．外12在三棱柱中，已知底面为正三角形，平面，，，则该三棱柱外接球的表面积为（）A．B．C．D．答案A解答取中点为点，连接，设的外心为，三棱柱外接球球心为，连接，，为正三角形，点为的重心，又，，，，则，又平面，平面，为直角三角形，，，则外接球表面积，故选．13矩形中，，，沿将矩形折起，使面面，则四面体的外接球的体积为（）A．B．C．D．答案C解答如图所示，取中点，则中，，在中，，，即为外接球球心，半径，又，，体积，故选．14已知矩形，，，为的中点现分别沿，将，翻折，使点，重合，记为点，则几何体的外接球表面积为．答案．解答由，，为中点，可得，，，，为长方体一角，其外接球直径为其体对角线长，，，外接球表面积为．15如图，边长为的正方形中，点，分别是边，的中点，、、分别沿、、折起，使，，三点重合于点，若四面体的四个顶点在同一个球面上，则该球的半径为（）A．B．C．D．答案B解答由题意知为等腰直角三角形，即，且，，，巩固练习：平面，四面体的外接球与以四面体扩展的长方体外接球是同一个，，故选．16如果一个球的外切圆锥的高是这个球的半径的倍，则圆锥的侧面面积和球的表面积之比为（）A ．B ．C ．D ．答案C解答如图所示，由于球的外切圆锥的高为球半径的倍，图中为球心，，，为圆锥的高，则设，，，与相似，又，，，，圆锥侧面积为侧，球的表面积为球，圆锥的侧面面积和球的表面积之比为：侧球,故选．17已知三棱锥的所有顶点都在球的球面上，是边长为的正三角形，为球的直径，且，则此棱锥的体积为（）A ．B ．C ．D ．答案A 解答如图，取中点，则为外接球球心，过点作底面，由于底面三角形是正三角形，所以是底面三角形的中心，连结并延长交于点，过点作交于点，则是三棱锥的高，正三角形边长为，，，又，，，，又，三棱锥，故正确．18设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为（）A．B．C．D．答案B解答由题意可知，该球的球心在两底面中心的连线的中点处，则球的半径，该球的表面积为：，故选．19已知圆锥的高为，底面圆的半径为，它的顶点和底面的圆周都在同一个球的球面上，则该球的表面积为（）A．B．C．D．答案B解答如图所示，设为球心，为底面圆心，则，，，在中，，即，解得，表面积，故选．20底面边长为的正三棱锥的内切球半径为，则其外接球的表面积为（）A．B．C．D．答案A解答由题可知：设该正三棱锥为，底面所对应的正三角形的高为，则，，，，，即，解得，，设外接球的半径为，则可建立勾股定理得，，解得，由球的的表面积得，　，故选．21在长方体中，，是的中点，则三棱锥外接球的表面积为（）A．B．C．D．答案B解答如图，取中点，中点，连接，则平面，点为的外心，三棱锥外接球圆心在上，连接，则，平面平面，，又，，，设，则，，即，解得，点与点重合，，，表故选．22已知正四棱锥的各顶点都在同一球面上，底面正方形的边长为，若该正四棱锥的体积为，则此球的体积为（）A．B．C．D．答案C解答设正四棱锥的高为，外接球半径为，，，该棱锥底面外接圆半径，该外接球球心所在圆截面如图所示，，，，该外接球体积为，故选．23已知三棱锥中，底面，，，，，则该三棱锥的内切球的体积为．答案．解答设内切球的半径为，以球心为顶点，三棱锥的三个面作为底面把大三棱锥分为四个小三棱锥，则可由等体积法得：大的三棱锥体积等于四个小三棱锥体积之和，又底面，，，，，，，，又，，由等体积得，，，由球的体积得，　．24将棱长为的正方体木块削成一个体积最大的球，则该球的体积为（）A．B．C．D．答案A解答将正方体木块削成一个体积最大的球，即求该正方体内切球的体积，则该球的半径为，，球故选．25点，，，在同一个球面上，，，若球的表面积为，则四面体体积最大值为（）A．B．C．D．答案C解答设球的半径为，则，，又，，，为等腰直角三角形，设为斜边上的中点，则为外接圆圆心，设为球心，则面，在中，，又为定值，最大，即为到面的距离最大，延长交球于，此时最大，有，，故选．26在正四面体中，是棱的中点，是棱上一动点，的最小值为，则该正四面体的外接球面积是．答案．解答由题可得，将正四面体展开成菱形，连接，交于，如图所示，则长即为最小值，即，，为中点，，设，，由余弦定理得，，，，正四面体棱长为，将正四面体可补形为正方体，棱长为正方体面对角线，补形得正方体棱长为，其外接球半径为，其外接球表面积为．27已知在直角梯形中，，，，将直角梯形沿折叠成三棱锥，当三棱锥的体积取最大值时，其外接球的体积为．答案．解答由题意，直角梯形中，，，，如图所示，取的中点，连接，连接、交于点，，直角梯形中，，四边形是正方形，，，将其沿折叠成三棱锥如下图所示：，为点到平面的距离，当平面平面时，最大，即有最大值，连接，平面平面，，平面，平面，，在中，，，，外接球的球心在点上，半径，．外接球28三棱锥中，平面，，的面积为，则三棱锥的外接球体积的最小值为（）A．B．C．D．答案D解答如图，平面，平面，，，设，则，在中，，令的外接圆半径为，则，三棱锥外接球直径为，，当且仅当，即时，等号成立，，即三棱锥的外接球体积最小值为，故选．29三棱锥内接于半径为的球，过球心，当三棱锥体积取得最大值时，三棱锥的表面积为（）A．B．C．D．答案D解答三棱锥内接于半径为的球，过球心，如下图所示，当在点的正上方，时，三棱锥体积最大，此时，，，，与是正三角形，，，表故选．30如图，在三棱锥中，平面平面，，，现将一小球放入三棱锥内，往三棱锥内注水，当注水的体积是三棱锥的体积的时，小球恰与该三棱锥各侧面及水面相切（小球完全浮在水面上方），则小球的表面积等于．答案．解答如下图，分别取、、、中点、、、，连接，，，，，，设则，，，，，，，相似比都是，，，公共，≌，，，面，面，又，面面，，为中点，，平面平面，平面平面，，面，已证面面，面，，，，同理可得，，，，，，，，，，即，，，即面是水面，≌，，，，面，面，，，，，，，，，同理可得，，表表，球．31已知三棱柱的侧棱垂直于底面，该棱柱的体积为，，，，若在该三棱柱内部有一个球，则此球表面积的最大值为（）A．B．C．D．答案C解答，，，可知为直角三角形，，，设内切圆半径为，可知，，，内切圆半径为，又柱体的体积为，且侧棱垂直于底面，，，，可知在该三棱柱内部有一个球的最大半径为，由球的表面积得：　，故选．32正三棱锥的高为，底面边长为，内有一个球与它的四个面都相切．(1)棱锥的表面积；(2)内切球的表面积与体积．(1)答案．解答正三棱锥的高为，底面边长为，可知底面正三角形的高为，可得侧面等腰三角形的高为，，可知表底侧．(2)答案表面积，体积．解答设球的半径为，以球心为顶点，棱锥的四个面为底面，把正三棱锥分为三个小三棱锥，则根据等体积得：，，由球的表面积公式得：，由球的体积公式得：．33边长为的等边的三个顶点，，都在以为球心的球面上，若球的表面积为，则三棱锥的体积为．答案．解答设球的半径为，，，连接外接圆圆心与球心，，如图所示，平面，，在等边三角形中，，，，又，．34已知球面上有四个点，，，，球心为点，在上，若三棱锥的体积的最大值为，则该球的表面积为．答案．解答由题可得，为三棱锥外接球直径，当为等腰直角三角形，底面面积最大，面面，且等腰时，过点到平面的高最大，此时，高就是．此时，，三棱锥体积为，，球的表面积为．35在三棱锥中，平面，，，，，则该三棱锥的外接球表面积为．答案．解答在中，由余弦定理得，，，由正弦定理可得，外接圆直径为，平面，，三棱锥外接球半径为，，该外接球的表面积为．36已知三棱锥的所有顶点都在球的球面上，是球的直径．若平面平面，，，三棱锥的体积为，则球的表面积为．答案解答设球的半径为，是球的直径，，，三角形与三角形都是等腰直角三角形，有，且、．平面平面，，是等腰直角三角形，且面．三棱锥的体积为，，解得．球的表面积为：．37一个几何体的三视图如图所示，其中正视图是一个正三角形，俯视图是一个等腰直角三角形，则该几何体的外接球的表面积为．答案．解答由三视图可知该几何体为三棱锥，作出原图如下：其中面平面，，平面，其外接球的球心在上，设球心为，，则，解得，外接球的半径，外接球的表面积为．38如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，若该几何体的顶点都在球的球画上，则球的表面积是（）A．B．C．D．答案A解答由三视图可知：该几何体为三棱锥，如图所示，则有面，，且，，，故其外接球半径，其表面积，故选．39在三棱锥中，，，，的中点为，的余弦值是，若，，，都在同一球面上，则该球的表面积是（）A．B．C．D．答案C解答根据题意作出下图，，，，又为中点，，为等边三角形，则，根据余弦定理：，，，，，，，，，，，面，面，面，，又，，面，又，三棱锥可看成长方体一角，外接圆半径，，，，球，，故选．40在三棱锥中，，，，，，且三棱锥的外接球的表面积为，则（）A．B．C．D．答案B解答，，，，为，，又，，、均在面内，面，又，外接圆半径①，又外接球表面积为，，②，联立①②可得，（舍去），故选．41已知，，，是球的球面上四个不同的点，若，且平面平面，则球的表面积为（）A．B．C．D．答案A解答分别取和的外心，，分别过，作平面和平面的垂线相交于点，即为球心，取中点，连接，，则，，如图所示：，出门测（15分钟）可知，又、为三角形的外心，，四边形为正方形，且边长为，，，球的半径为，球的表面积，故选．42已知三棱锥的所有顶点都在球的球面上，是球的直径，是等腰直角三角形，，若，三棱锥的体积是，则球的表面积为．答案．解答可将三棱锥在长方体中还原，如图所示，，，，，，三棱锥的外接球与长方体的外接球相同，，球的表面积为．43直三棱柱中，已知，，，，若三棱柱的所有顶点都在同一球面上，则该球的表面积为．答案．解答在直棱柱中，，故可将其变形为长方体，其中，、、为长方体的棱，该三棱柱外接球半径为：，该外接球表面积为．44已知圆锥的侧面展开图是一个半径为的半圆，若该圆锥的顶点及底面圆周在球的表面上，则球的体积为（）A．B．C．D．答案A解答设圆锥的高为，底面圆的半径为，，，，，球即该圆锥的外接球，设球的半径为，，，，球的体积为：，故选．45如图，虚线小方格是边长为的正方形，粗实（虚）线为某几何体的三视图，则该几何体外接球的表面积为（）A．B．C．D．答案D解答由题可得，该几何体的直观图如图所示，其中，，即为该几何体外接球直径，由三视图可得，，，该外接球的表面积为，故选．46如图，网格纸上小正方形的边长为，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的表面积为（）A．B．C．D．答案B解答由题意可知该几何体是三菱锥，把该三棱锥放入长宽高分别为，，的长方体中，则该三棱锥的外接球，即为长方形的外接球，如图所示：且外接球的直径为，所以该外接球表面记为，故选．47如图，在四面体中，平面，是边长为的等边三角形．若，则四面体外接球的表面积为．答案．解答由正弦定理可得，正的外接圆直径为，设四面体的外接球半径为，平面，，，，四面体外接球的表面积为．48某三棱锥的三视图如图所示，其侧（左）视图为直角三角形，则该三棱锥外接球的表面积为（）A．B．C．D．答案A解答该几何体的直观图如图所示：由三视图及图象可知：、、两两垂直，则三棱锥可补为以、为邻边的长方形为底面，为侧棱的长方体，其外接球半径为，外接球表面积．49中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．如图为一个阳马与一个鳖臑的组合体，已知三棱锥为鳖臑，且平面，，，该鳖臑的外接球的表面积为，则阳马的外接球的体积为（）A．B．C．D．答案D解答由题可得，在三棱锥中，，平面，，，即、、两两垂直，三棱锥的外接球直径，设，，三棱锥的外接球表面积为，，，，在阳马四棱锥中，、、两两垂直，其外接球直径为，，，其外接球的体积为，故选．41。

内切球和外接球问题课件

• 结论1：正方体或长方体的外接球的球心其体对角线的中点。
• 结论2：正棱柱的外接球的球心是上下底面中心的连线的中点。
• 结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
• 结论4：正棱锥的外接球的球心在其高上，具体位置可通过计算找到。
• 结论5：若棱锥的顶点可构成共斜边的直角三角形，则公共斜边的中点就是其外接球的球心。
正方体的内切球
例1
将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为 4
直棱柱的外接球
例2
已已知知直直三三棱棱柱柱AABBCCA1AB11BC11C的1的六六个个顶顶点点都在都在球球OO的的球球面面上上,,若若AABBBCBC 1,1,ABACBC12012,0, AAAA11 22 33，，则则球球OO的的表表面面积积为为
几何体外接：一个几何体所有顶点都在另一个几何体表面上。
正方体的内切球、棱切球、外接球
• 三、几何体的外接球与内切球问题：
• 1、外接球的问题： • 几何体外接球问题是立体几何中的难点和重要的
考点，此类问题实质是解决球的半径或确定球心0 的位置问题，其中球心的确定是关键。 • (1)由球的定义确定球心 • 在空间，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心。 • 由上述性质，可以得到确定简单多面体外接球的球心的如下结论。
• 途径3：若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体．
• 途径4：若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．
(3)由性质确定球心利用球心与截面圆圆心的连线垂直于截面圆及球心与弦中点的连线垂直于弦的性质，确定球心．内切球的问题对内切球有以下几点认识： 1、内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等。 2、正多面体的内切球和外接球的球心重合。 3、正棱锥的内切球和外接球球心都在高线上，但不重合。 4、基本方法：构造三角形利用相似比和勾股定理。 5、体积分割是求内切球半径的通用做法。

难点突破：立体图形的外接球与内切球问题

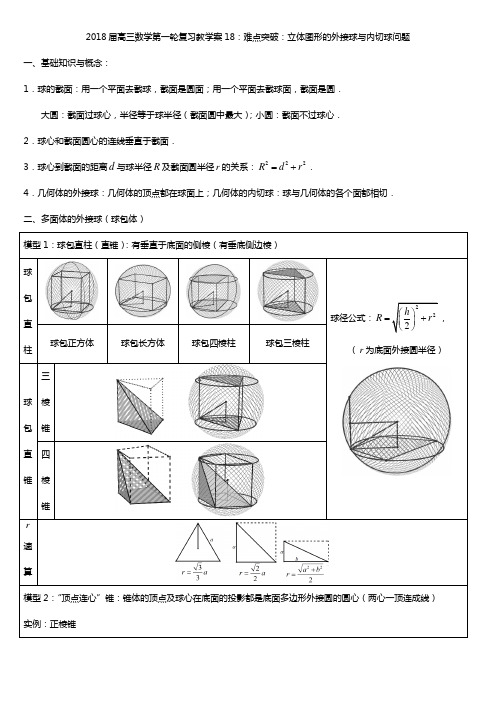
2018届高三数学第一轮复习教学案18：难点突破：立体图形的外接球与内切球问题一、基础知识与概念：1．球的截面：用一个平面去截球，截面是圆面；用一个平面去截球面，截面是圆．大圆：截面过球心，半径等于球半径（截面圆中最大）；小圆：截面不过球心．2．球心和截面圆心的连线垂直于截面．3．球心到截面的距离d与球半径R及截面圆半径r的关系：222R d r=+．4．几何体的外接球：几何体的顶点都在球面上；几何体的内切球：球与几何体的各个面都相切．二、多面体的外接球（球包体）模型1：球包直柱（直锥）：有垂直于底面的侧棱（有垂底侧边棱）球包直柱球径公式：222hR r⎛⎫=+⎪⎝⎭，（r为底面外接圆半径）球包正方体球包长方体球包四棱柱球包三棱柱球包直锥三棱锥四棱锥r速算模型2：“顶点连心”锥：锥体的顶点及球心在底面的投影都是底面多边形外接圆的圆心（两心一顶连成线）实例：正棱锥球径计算方程：()222h R r R -+=2222202h r h hR r R h+⇒-+=⇒=，（h 为棱锥的高，r 为底面外接圆半径）特别地，（1）边长为a 正四面体的外接球半径：R =______________．（2）底面边长为a ，高为h 的正三棱锥的外接球半径：R =__________．（3）底面边长为a ，高为h 的正四棱锥的外接球半径：R =__________．例：1．（2017年全国卷III 第8题）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．34πC ．2π D ．4π 【解析】模式辨识：“球包体”中的“垂底侧边棱（母线）”类型，1h =，1R =，底面半径为r ，则由222h R r⎛⎫=+ ⎪⎝⎭得：222213124r r ⎛⎫=+⇒= ⎪⎝⎭，234V r h ππ==．2．（2010年全国新课标卷第10题）设三棱柱的侧棱垂直于底面，所有棱的长都为a ，顶点都在一个球面上，则该球的表面积为A ．2a πB ．273a πC ．2113a πD ．25a π【解析】“球包体”中的“垂底侧边棱”类型，h a =，3r =，222222724312h a a a R r ⎛⎫=+=+= ⎪⎝⎭，所以该球的表面积2227744123a a S R ππ==⨯=．答案B ． 3．（2014年全国大纲卷第8题）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为A ．814πB ．16πC ．9πD ．274π【解析】模式辨识：“球包体”中的“顶点连心锥”，4h =，222r ==221629284h r R h ++===，所以2818144164S R πππ==⨯=，答案：A ． 4．（2013年全国卷I 第6题）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为A ．35003cm πB ．38663cm πC ．313723cm πD ．320483cm π【解析】设水面与球的接触点（切点）为P ，球心为O ，则PO 垂直于正方体的上表面，依题意P 到正方体上表面的距离为2h =，球与正方体上表面相交圆的半径4r =，有：()2222R r R -+=，2454r R +⇒==，所以球的体积3450033V R ππ==．三、定心大法：球心在过截面圆的圆心且垂直于截面圆所在平面的直线上．两圆定心法：如下图，过两个截面圆的圆心分别作相应截面圆的垂线，由两垂线的交点确定圆心．例2：1．已知边长为23的棱形ABCD 中，60∠=︒，现沿对角线BD 折起，使得二面角A BD C --为120︒，此时点A ，B ，C ，D 在同一个球面上，则该球的表面积为（）A ．20πB ．24πC ．28πD ．32π2．在矩形ABCD 中，4AB =，3BC =，沿AC 将矩形折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为___________．3．在边长为1的菱形ABCD 中，60BAD ∠=︒，沿对角线将菱形折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为_____________．四、正多面体的内切球（体中球）锥体的内切球：R =____________．圆锥的内切球：R =边长为a 的正方体： 2aR =等边圆柱（母线a ）：R =2a ．边长a 的正八面体：R =五、正多面体的“切边球”（与所有的棱都相切的球）正四面体边长为a ，球半径R =正方体边长为a ，球半径R =正四面体边长为a ，球半径R =例3：1．一个球的外切正方体的全面积为6，则球的体积为_________．2．某圆锥的截面为边长为2的正三角形，则该圆锥的内切球的表面积为_______．3．（2016年全国卷III 第10题）在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是A ．4πB ．92πC ．6πD ．323π【解析】考查直三棱柱中截面的内切圆为球的大圆的情景，有()13681068222AA R R ++=⨯⇒=>=，故当球半径为32时球的体积最大为344273382V R πππ9==⨯=．答案B ．练习：1．（2015年全国卷II 第9题）已知A ，B 是球O 的球面上两点，90AOB ∠=︒，C 为该球面上的动点，若三棱锥O ABC -体积的最大值为36，则球O 的表面积为A ．36πB ．64πC ．144πD ．256π2．（2016年福建漳州市5月质检）三棱锥S ABC -中，SB ⊥平面ABC ，5SB =ABC ∆3的正三角形，则三棱锥S ABC -的外接球的表面积为（）A ．3πB ．5πC ．9πD ．12π3．（2014年湖南卷）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（）A ．1B ．2C ．3D ．44．（2013年辽宁卷理10）已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上，若3AB =，4AC =，AB AC ⊥，112AA =，则球O 的半径为（）A 317B ．10C ．132D ．3105．（2012年全国新课标卷第11题）已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为A ．26B ．36C ．23D ．226．在正三棱锥P ABC -中，3PA PB PC ===，侧棱PA 与底面ABC 所成的角为60︒，则该三棱锥外接球的体积为（）A ．πB ．3πC ．4πD ．43π 7．已知底面边长为12的正四棱柱的各顶点均在同一个球面上，则该球的体积为（）A ．323πB ．4πC ．2πD ．43π 8．（2017年福建省质检）．空间四边形ABCD 的四个顶点都在同一球面上，E 、F 分别是AB 、CD 的中点，且,EF AB EF CD ⊥⊥，若8,4AB CD EF ===，则该球的半径等于A ．65216B ．28C ．652D 659．若三棱锥P ABC -的最长的棱2PA =，且各面均为直角三角形，则此三棱锥的外接球的体积是__________． 10．（2008年高考浙江卷理14）已知球O 的面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB BC ⊥，3DA AB BC ===，则球O 的体积为____________．11．（2016年东北三省三校联考）三棱柱111ABC A B C -各顶点都在一个球面上，侧棱与底面垂直，120ACB ∠=︒，23CA CB ==14AA =，则这个球的表面积为____________．12．在三棱柱111ABC A B C -中，侧棱1AA 垂直底面，90ACB ∠=︒，30BAC ∠=︒，1BC =，且三棱柱111ABC A B C -的体积为3，则三棱柱111ABC A B C -的外接球表面积为_________．13．在正三棱锥S ABC -中，M ，N 分别是棱SC 、BC 的中点，且AM MN ⊥，若侧棱23SA =，则正三棱锥S ABC -外接球的表面积是____________．14．在三棱锥A BCD -中，2AB CD ==，5AD BC ==7AC BD ==，则三棱锥A BCD -外接球的表面积为__________．15．（2017年天津卷）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为______．16．（2017年江苏卷）如图，在圆柱12O O 内有一个球，该球与圆柱的上、下底面及母线均相切，记圆柱12O O 的体积为1V ，球O 的体积为2V ，则12V V 的值是_____________．。

《空间几何体的外接球》教学设计方案

《空间几何体的外接球》教学设计方案《《空间几何体的外接球》教学设计方案》这是优秀的教学设计文章，希望可以对您的学习工作中带来帮助！学习主题介绍学习主题名称：《空间几何体的外接球》主题内容简介：通过例题发现与探究空间几何体的外接球问题，并归纳长方体、直三棱柱、可以补形为直三棱柱的三棱锥、正棱锥的外接球的求解方法。

学习目标分析知识目标：理解空间几何体外接球的特征与性质，掌握几种常见几何体的外接球的求解方法。

能力目标：培养学生观察、分析、归纳、推理的能力；在掌握求解长方体和直三棱柱的外接球的前提下，通过方法迁移与问题化归来研究可以补形为直三棱柱的三棱锥的外接球的方法，培养学生的知识、方法迁移能力；培养学生自主探究、合作探究的能力；提高分析问题和解决问题的能力。

情感目标：培养学生善于观察，勇于探究的创新精神，提高直观想象的核心素养。

学情分析前需知识掌握情况：本节课之前，学生已经在高二时学过了立体几何，对空间几何体的结构特征、体积和面积的相关公式已经比较熟悉了。

在高三高考第一轮复习时，学生对知识的掌握有点回生，并且之前也没有全面地对各种几何体的外接球求解方法进行系统的归纳与总结。

学生直观想象以及作图能力有所欠缺，在解立体几何问题过程中经常出现方法不懂、运算出错的问题。

对微课的认识：现在的网络教学比较普遍，高三学生或多或少已经有接触过，而微课相对于网络课更简洁、更有针对性，学生对微课更有新鲜感和期待。

微课可重复播放，能帮助学困生避免似懂非懂，而又无法重构课堂老师讲解的场面，学生通过多次学习微课可以熟练掌握知识与方法，进而解决问题。

微课也有利于学生分层教学，提高教学的针对性和效率。

学生特征分析学习态度：利用微课进行辅助教学或自主学习，能给学生提供直观的画面，学生会更加感兴趣，学习也更加的专注。

学习风格：微课的画面感和动画感比较强，并且课件制作精良。

老师所制作的微课也是通过多次的演练而成，授课的过程语言简洁，分析问题精准到位，往往能激发学生的学习热情。

2022年高中数学新北师大版精品教案《球的内切与外接的解技巧》

【高考地位】球作为立体几何中重要的旋转体之一，成为考查的重点，根本属于必考题目．而且球相关的特殊距离，即球面距离是一个备考的重点，要熟练掌握根本的解题技巧．还有球的截面的性质的运用，特别是其它几何体的内切球与外接球类组合体问题，更应特别加以关注的．题目一般属于中档难度，往往单独成题，或者在解答题中以小问的形式出现．【方法点评】类型一球的内切问题使用情景：有关球的内切问题解题模板：第一步首先画出球及它的内切圆柱、圆锥等几何体，它们公共的轴截面；第二步然后寻找几何体与几何体之间元素的关系第三步得出结论例1．如图1所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切．〔1〕求两球半径之和；〔2〕球的半径为多少时，两球体积之和最小．【答案】〔1〕；〔2〕当时，体积之和有最小值．【点评】此题的关键在于作截面，一个球在正方体内，学生一般知道作对角面，而两个球的球心连线也应在正方体的体对角线上，故仍需作正方体的对角面，得如图2的截面图，在图2中，观察与和棱长间的关系即可．【变式演练1】一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？【答案】球取出后，圆锥内水平面高为．【解析】又，那么，解得．答：球取出后，圆锥内水平面高为．【点评】先作出轴截面，弄清楚圆锥和球相切时的位置特征，利用铁球取出后，锥内下降局部圆台的体积等于球的体积，列式求解．考点：空间几何体的体积；【变式演练2】正三棱锥的高为1，底面边长为，正三棱锥内有一个球与其四个面相切．求球的外表积与体积．【答案】，．∴得：，∴．∴．【点评】球心是决定球的位置关键点，此题利用球心到正三棱锥四个面的距离相等且为球半径来求出，以球心的位置特点来抓球的根本量，这是解决球有关问题常用的方法．比方：四个半径为的球两两外切，其中三个放在桌面上，第四个球放在这三个球之上，那么第四个球离开桌面的高度为多少？这里，四个球的球心这间的距离都是，四个球心构成一个棱长为的正四面体，可以计算正四面体的高为，从而上面球离开桌面的高度为．考点：空间几何体的球体积和外表积【变式演练3】把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．【答案】．考点：空间几何体的球体积和外表积【变式演练4】三棱锥，满足两两垂直，且，是三棱锥外接球上一动点，那么点到平面的距离的最大值为【答案】【解析】试题分析：由，可将三棱锥放入正方体中，其长宽高分别为，那么到面距离最大的点应该在过球心且和面垂直的直径上，因为正方体的外接球直径和正方体的体对角线长相等，那么那么到面距离的最大值为考点：三棱锥的外接球【思想点睛】空间几何体与球接、切问题的求解方法1求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．2假设球面上四点II，文15】长方体的长、宽、高分别为，其顶点都在球的球面上，那么球的外表积为【答案】【解析】球的直径是长方体的体对角线，所以【考点】球的外表积【名师点睛】涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体中的特殊点一般为接、切点或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径直径与该几何体量的关系，列方程组求解【反应练习】１．一个圆锥内接于球〔圆锥的底面圆周及顶点均在球面上〕，假设球的半径，圆锥的高是底面半径的2倍，那么圆锥的体积为___________．【答案】考点：圆锥与球．２．设三棱柱的侧棱与底面垂直，，，假设该棱柱的所有顶点都在体积为的球面上，那么直线与直线所成角的余弦值为〔〕A． B． C．D．【答案】B【解析】试题分析：由，假设棱柱的所有顶点都在球面上，那么同高的长方体个顶点也在球面上，且外接球的直径为长方体的体对角线，由球体体积可得直径为，由于长方体底面为边长为的正方形，故侧面的对角线为，由余弦定理可知，直线与直线所成角的余弦值为考点：三棱柱外接球、异面直线所成角．【方法点睛】构造长方体或正方体确定球心：⑴正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥⑵同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥⑶假设棱锥含有线面垂直关系，那么可将棱锥补成长方体或正方体⑷假设三棱锥的三个侧面两两垂直，那么可将三棱锥补成长方体或正方体３．【2021河省衡水第一中学模拟】某棱锥的三视图如下图，那么该棱锥的外接球的外表积为〔〕A B C D【答案】A，利用正弦定理可以求出的外接圆半径，，，平面，那么，那么球的半径，外接球的外表积为，选A4 【2021湖南湘东五校联考】正三棱锥N∥，∥,所以就是和所成角，而是等边三角形，所以故填11【2021湖南衡阳第八中学模拟】三棱锥，在底面中，，，面，，那么此三棱锥的外接球的外表积为______【答案】。

高考数学一轮复习第六章专题六几何体的外接球与内切球问题课件

)
A.4 3π
B.8π
C.12π
D.20π
解析：在底面△ABC 中，由正弦定理得底面△ABC 外接圆的
半径为
r＝2sin B∠CBAC＝2sin2
3π＝ 4
2.
直三棱柱 ABC-A1B1C1 的外接球的半径 R＝ ( 2)2＋12＝ 3，
r2＋A2A12＝
则直三棱柱 ABC-A1B1C1 的外接球的体积为43πR3＝4 3π.
当
λ＝12时，cos〈E→B，E→G〉＝2
3
2 .
∴cos〈E→B，E→G〉的最大值为2
3
2 .
∵A→C＝(－1，1，0)，A→F＝(0，1，1)， ∴E→B·A→C＝E→B·A→F＝0. ∴EB⊥AC，EB⊥AF. ∵AC∩AF＝A，∴EB⊥平面 AFC. ∵E→B·E→G>0，∴cos〈E→B，E→G〉即为 EG 与平面 AFC 所成角
如图 6-7 所示，把四面体 S-ABC 补全为长方体 ABCD-SPMN，其中 SA，AB，BC 为长方体中首尾相连且两两相互垂直的三条棱，点 H 为 PM 中点.
图 6-7
∵GH∥AP，∴G，H 两点到平面 AEF 的距离相等.
设点 H 到平面 AEF 的距离为 d.
∵△APF 是边长为 2 2的等边三角形，
[例 1]已知一个圆锥底面半径为 1，母线长为 3，则该圆锥内
切球的表面积为( )
A.π
B.32π
C.2π
D.3π
解析：依题意，作出圆锥与球的轴截面，如图
6-1 所示.设球的半径为 r，易知轴截面三角形边 AB
上的高为 2 2，因为△SOD∽△SBE，所以SSOB＝OBED，
即2 32－r＝1r，解得 r＝ 22.所以圆锥内切球的表面

外接球与内切球讲义

A. 4π
B. 12π
C. 16π
D.
32 3
π
·8· 惊叹数学的波澜壮阔之势赏析数学的对称和谐之美！
领悟数学的高瞻远瞩之能铸就数学的茅塞顿开之境！
学习数学领悟数学满分数学
7. (2021• 咸阳模拟 ) 在直三棱柱 ABC
- A1B1C1 中，AB = BC = 2，∠ABC =
π 2
，若该直三棱柱的外接球表面积
棱锥体积的最大值为
3
3 4
，则其外接球的半径为
(
)
A. 1
B. 2
C. 3
D.
2 3
3 ，AC = 3，若该三
考点四含二面角的外接球终极公式
双距离单交线公式：R2 =
m2 + n2 − 2mncosα sin2α
+
l2 4
如下图，若空间四边形 ABCD 中，二面角 C − AB − D 的平面角大小为 α，ABD 的外接球球心为 O1，ABC 的外
为 16π，则此直三棱柱的高为（）
A. 4
B. 3
C. 4 2
D. 2 2
图1
图2
8. (2021• 呼和浩特一模 ) 四面体 ABCD 的四个顶点都在球 O 上，且 AB = AC = BC = BD = CD = 4，AD =
2 6 ，则球 O 的表面积为（）
A.
70π 3
B.
80π 3
C. 30π
接球球心为 O2，E 为公共弦 AB 中点，则 ∠O1EO2 = α，O1E = m，O2E = n，AE =
l 2
，OA = R，由于 O、O1、E、O2
四点共球，且 OE = 2R =

空间几何体的外接球和内切球问题讲课教案

空间几何体的外接球和内切球问题空间几何体的外接球和内切球问题类型1 外接球的问题1.必备知识：(1)简单多面体外接球的球心的结论.结论1：正方体或长方体的外接球的球心是其体对角线的中点.结论2：正棱柱的外接球的球心是上下底面中心的连线的中点.结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.(2)构造正方体或长方体确定球心.(3)利用球心O 与截面圆圆心O 1的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质，确定球心.2.方法技巧：（1）几何体补成正方体或长方体.（2）轴截面法（3）空间向量法1AB DC AD BC BD AC ======例1-1、正四面体的棱长都为，求此四面体外接球和内切球的半径例1-2、四面体中，，求此四面体外接球的表面积例1-3．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（）A.3B.6C.36D.9训练1（创新110页）某几何体的三视图如图所示，则该几何体的外接球的表面积为( )A.25πB.26πC.32πD.36π训练2（创新110页）已知边长为2的等边三角形ABC ，D 为BC 的中点，沿AD 进行折叠，使折叠后的∠BDC ＝π2，则过A ，B ，C ，D 四点的球的表面积为( ) A.3π B.4π C.5π D.6π例2-1（创新110页）体积为3的三棱锥P －ABC 的顶点都在球O 的球面上，P A ⊥平面ABC ，P A ＝2，∠ABC ＝120°，则球O 的体积的最小值为( ) A.773π B.2873π C.19193π D.76193π 例2-1（创新109页）三棱锥P －ABC 中，平面P AC ⊥平面ABC ，AB ⊥AC ，P A ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为( )A.23πB.234πC.64πD.643π 类型2 内切球问题1.必备知识：(1)内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.(2)正多面体的内切球和外接球的球心重合. (3)正棱锥的内切球和外接球球心都在高线上，但不一定重合.2.方法技巧：体积分割是求内切球半径的通用做法.【例3】体积为4π3的球与正三棱柱的所有面均相切，则该棱柱的体积为________. 空间几何体的外接球和内切球问题近几年高考题1、（2019全国1卷第12题）已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，△ABC 是边长为2的正三角形，E ，F 分别是PA ，PB 的中点，90CEF ∠=︒，则球O 的体积为（）A ．B ．C ． D2、（2018全国3卷第10题）．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为（）A ．B ．C ．D ．3．（2017全国1卷第16题）如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为______．4、（2017新课标全国Ⅲ理科）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A.πB.3π4 C.π2 D.π4 5、（2016年全国1卷第6题）．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是 ( )（A ）17π （B ）18π （C ）20π （D ）28π6、（2016年全国3卷第10题）在封闭的直三棱柱ABC −A 1B 1C 1内有一个体积为V 的球，若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是( ) (A)4π (B)9π2 (C)6π (D)32π37、（2015年全国1卷第11题）．圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π，则r=（）（A ） 1 （B）2 （C ）4 （D ）88、（2015年全国2卷第9题）．已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为（） A ．36πB ．64πC ．144πD ．256π 7.(2014·大纲全国，8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4B.16πC.9πD.27π49、（2013年课标1卷第6题）、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 310、（2012课标卷第11题）已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（）()A 26 ()B 36 ()C 23 ()D 2211、（2011课标卷第15题）已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为。

球的内切和外接问题课件ppt课件

ppt课件
10
2、构造长方体已知A点B A、6,BA、C=C2、1D3在,A同D一=8个，球则面B上、，CA两B点间平的面A 球BC面D距离B是C 34DC.
O
B C
D 图 5
ppt课件
11
三、确定球心位置法
在矩形ABCD中，AB=4，BC=3，AC沿将矩形
ABCD折成一个直二面角B-AC-D，则四面体 ABCD的外接球的体积为( Ｃ )
2
2
在RtAOO1中，由勾股定理得，R2
2 3

R

3 3

，解得R

6, 4
V球

4 R3 3

4 3

6 4
3

6 . 8
ppt课件
14
六、寻求轴截面圆半径法
正四棱锥S-ABCD的底面边长和各侧棱长
都为 2，点S,A,B,C,D都在同一球面上，
ppt课件
1
一、直接法
A
C
O
A1
C1
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一
球面上，则该球的表面积为 27 .
变式题：一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体
积为 4 3 .
ppt课件
2
2、求长方体的外接球的有关问题
例2、一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3 ，则此球的表面积为 .
A.125
12
B.125
9
C.125
6
D.125
3
D
AO

内切球和外接球常见解法讲课稿

内切与外接1 球与柱体1.1 球与正方体例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（）A ．22B ．1C ．212+D 21.2 球与长方体长方体各顶点可在一个球面上，故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时，截面图为长方体的对角面和其外接圆，和正方体的外接球的道理是一样的，故球的半径2222l a b c R ++== 例 2 在长、宽、高分别为2，2，4的长方体内有一个半径为1的球，任意摆动此长方体，则球经过的空间部分的体积为( )A.10π3B.4πC.8π3D.7π31.3 球与正棱柱例3 正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最值，为 .2 球与锥体规则的锥体，如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合，以外接和内切两种形态进行结合，通过球的半径和棱锥的棱和高产生联系，然后考查几何体的体积或者表面积等相关问题.2.1 球与正四面体2222233a R r a R r CE +=-=，=，解得：66,.R r ==例4 将半径都为１的四个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为 ( ) A.3263+ B. 2+263 C. 4+263 D. 43263+2.2 球与三条侧棱互相垂直的三棱锥例5 在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱 23SA =,则正三棱锥S-ABC 外接球的表面积是______2.3 球与正棱锥球与正棱锥的组合，常见的有两类，一是球为三棱锥的外接球，此时三棱锥的各个顶点在球面上，根据截面图的特点，可以构造直角三角形进行求解.二是球为正棱锥的内切球，例如正三棱锥的内切球，球与正三棱锥四个面相切，球心到四个面的距离相等，都为球半径R ．这样求球的半径可转化为球球心到三棱锥面的距离，故可采用等体积法解决，即四个小三棱锥的体积和为正三棱锥的体积.例6 在三棱锥P －ABC 中，PA ＝3侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（）A ．π B.3π C. 4π D.43π 接球的球心,则2SC R =. 例7 矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )A.π12125B.π9125C.π6125D.π3125 3 球与球对多个小球结合在一起，组合成复杂的几何体问题，要求有丰富的空间想象能力，解决本类问题需掌握恰当的处理手段，如准确确定各个小球的球心的位置关系，或者巧借截面图等方法，将空间问题转化平面问题求解.例7 在半径为R 的球内放入大小相等的4个小球，则小球半径r 的最大值为（）4 球与几何体的各条棱相切球与几何体的各条棱相切问题，关键要抓住棱与球相切的几何性质，达到明确球心的位置为目的，然后通过构造直角三角形进行转换和求解.例：与正四面体各棱都相切的球的半径为棱的一半：.例8 把一个皮球放入如图10所示的由8根长均为20 cm 的铁丝接成的四篇一：程序员实习总结范文以前在校很少自己做程序,对软件工程更是一无所知.来到公司,开始接触大规模(其实现在看来实习的项目其实还是很小的)软件开发,一时真的有些迷茫.比起VSS,MVC,QA,CMMI,我对JAVA,JSP,XML的一窍不通根本不值一提.大家都不想输在起点,所以都默契地在加班,这样一直持续了实习的两个月.刚来的时候始业教育显得慢吞吞,我们还经常盘算去哪哪玩之类的.我和FLYSKY(20个新生里唯一一个南区的兄弟,软件学院的)还经常出去吃各种小吃,每到一处都尝尝本地的风味,这是他的习惯.之后开始的培训还不是很难过,JAVA,C++,ORACLE,老师们讲的很好,可以说是非常好,好得我们没有几个人能听懂.大家开始发愁,我也是每天晚上都基本看书到10点.我心说得亏哥们我还练过,来之前的2月份我就自己买了一本THINKING IN JAVA,看懂看不懂怎么说也算是准备了一下JAVA.C++虽说没去上过课,但凭我的直觉我就一下看中这东西很有用,自己也看过一阵.至于ORACLE,虽然不了解,但毕竟因为佩服云飞扬的性格和敬业精神,咱SQL选修也不是白混的.专业倒还有点基础,再加上咱这自学能力也不是吹的,基本维持.可等到后来的日语课就全迷糊了:本就没有语言天赋,再加上记忆严重欠缺,总是特别害怕去上日语课.不过特别喜欢那个老师说话的感觉,加上她一直对我都很好,所以还是很用心的学着.随着培训的收尾,我们开始正式进入项目.从需求分析,概要设计到详细设计,我们一步一步的开始接触软件开发的每个细节.最受不了的就是每天都要记周报,填写自己的劳动成果.因为这个我还被QA通报了好几次呢,真的很郁闷.其实现在我很感谢这种制度化的东西,某些情况下好习惯的养成是要靠强制来确保的.详细设计之后就是企盼已久的编码,我心想终于可以做点正事了.现在回头一看才知道,其实编码只占软件开发的整个过程劳动量的1/4左右,而且其他的环节也不是想象中的那么无足轻重.编码我其实做的很不好,主要是因为需求分析阶段就没有认真仔细的理解需求和规格说明,加上编码时一个关键时段我回校和老同学叙旧.那阵项目经理(PM)就经常和我们说,有问题自己想办法,不要经常问我.PM其实是在叫我们自己酝酿,遇到难题只有憋一憋才能有真的收获.而我不在的那三天正好是大家技术/思路上的一个跃迁,很多难题的解决方法都基本成熟,大家的编码也接近50%了,所以回来时我感觉已经掉队很多.再一个就是编码中期时机器出问题,环境搭不上了,这使我更加紧张和急躁,大大影响了我的士气.后来利用五一其间的加班我终于赶完了自己的模块,达到了第一个里程碑.其实从发现落后到加班赶完这段经历,对我来说也具有里程碑的意义.不仅考验了我自己的能力和心理素质,也证明了我对集体的责任感和合作意识.我可以叫别人来帮我做赶上进度,但那样我会错过自己学习的机会,以后再遇到难题我还是不行;我也可以硬着头皮导致项目延期,那样我以后的日子保证不好过,而且这么做也不符合我的性格.事实证明我顶住压力独立完成任务不管是对集体还是对我个人都是一件大好事.紧张的编码之后是单体测试,很多人都在继续编码,原来大家的编码都是没有完全做完.本是自己给自己挑毛病的过程,我们却都用来完成之前没有完成的任务,说来不禁可笑.。

空间几何体的外接球与内切球优秀教学设计1

八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）.四、与台体相关的，此略.五、八大模型第一讲柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32解： 162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ；（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 π9 解：933342=++=R ，ππ942==R S ；（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理）AC(3)题-2（解答图）AC（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D 解：在ABC ∆中，7120cos 2222=⋅⋅-+=BC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BACBCr ，∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是解：由已知得三条侧棱两两垂直，设三条侧棱长分别为c b a ,,（+∈R c b a ,,），则⎪⎩⎪⎨⎧===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ，（6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为解：3)2(2222=++=c b a R ，432=R ，23=R πππ2383334343=⋅==R V 球，类型二、对棱相等模型（补形为长方体）题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=，补充：图2-1中，abc abc abc V BCD A 31461=⨯-=-. (6)题图（6）题直观图P图2-1第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .思考：如何求棱长为a 的正四面体体积，如何求其外接球体积？例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解：对棱相等，补形为长方体，如图2-1，设长宽高分别为c b a ,,，110493625)(2222=++=++c b a ，55222=++c b a ，5542=R ，π55=S(1)题图B（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 .π229 解：如图2-1，设补形为长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ， 229222=++c b a ，22942=R ，π229=S （3）正四面体的各条棱长都为2，则该正面体外接球的体积为（3）解答题解：正四面体对棱相等的模式，放入正方体中，32=R ，23=R ，ππ2383334=⋅=V （4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解：如解答图，将正四面体放入正方体中，截面为1PCO ∆，面积是2.类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ；第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）；第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为解：设正六边形边长为a ，正六棱柱的高为h ，底面外接圆的半径为r ，则21=a ，正六棱柱的底面积为833)21(4362=⋅⋅=S ，89833===h Sh V 柱，∴3=h ，4)3(14222=+=R也可1)21()23(222=+=R ），1=R ，球的体积为34π=球V ；（2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 .解：32=BC ，4120sin 322==r ，2=r ，5=R ，π20=S ；（3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .π16解：折叠型，法一：EAB ∆的外接圆半径为31=r ，11=OO ，231=+=R ；法二：231=M O ，21322==D O r ，4413432=+=R ，2=R ，π16=表S ；法三：补形为直三棱柱，可改变直三棱柱的放置方式为立式，算法可同上，略.换一种方式，通过算圆柱的轴截面的对角线长来求球的直径：162)32()2(222=+=R ，π16=表S ；（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解：法一：282164236162=⋅⋅⋅-+=BC ，72=BC ，37423722==r ，372=r ， 3404328)2(2122=+=+=AA r R ，π3160=表S ；法二：求圆柱的轴截面的对角线长得球直径，此略.第二讲锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-3图4-41．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；（3）题第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R ；事实上，ACP ∆的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=；第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 . 解：法一：由正弦定理（用大圆求外接球直径）；法二：找球心联合勾股定理，72=R ，ππ4942==R S ；（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为解：方法一：找球心的位置，易知1=r ，1=h ，r h =，故球心在正方形的中心ABCD 处，1=R ，34π=V 方法二：大圆是轴截面所的外接圆，即大圆是SAC ∆的外接圆，此处特殊，SAC Rt ∆的斜边是球半径，22=R ，1=R ，34π=V . （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（） A ．433 B ．33 C ．43 D ．123解：高1==R h ，底面外接圆的半径为1=R ，直径为22=R ，设底面边长为a ，则260sin 2==a R ，3=a ，433432==a S ，三棱锥的体积为4331==Sh V ；（4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60，则该三棱锥外接球的体积为（） A ．π B.3π C. 4π D.43π 解：选D ，由线面角的知识，得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上，在圆锥中求解，1=R ；（5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（）AA．6 B．6 C．3 D．2解：36)33(12221=-=-=r R OO ，362=h ，62362433131=⋅⋅==Sh V 球类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=.2．题设：如图5-1至5-8这七个图形，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )C A ．π3 B ．π2 C ．316πD ．以上都不对解：选C ，法一：（勾股定理）利用球心的位置求球半径，球心在圆锥的高线上，221)3(R R =+-,32=R ,ππ31642==R S ；法二：（大圆法求外接球直径）如图，球心在圆锥的高线上，故圆锥的轴截面三角形PMN 的外接圆是大圆，于是3460sin 22==R ，下略；第三讲二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步：先画出如图6所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ；第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,；第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 . 解：如图，3460sin 22221===r r ，3221==r r ，312=H O ， 35343121222=+=+=r H O R ，315=R ；法二：312=H O ，311=H O ，1=AH ， 352121222=++==O O H O AH AO R ，315=R ；（2）在直角梯形ABCD 中，CD AB //， 90=∠A ，45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解：如图，易知球心在BC 的中点处，π4=表S ；（1）题（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为 π6 解：如图，法一：33)2cos(cos 211-=+∠=∠πO OO B SO ， 33sin 21=∠O OO ，36cos 21=∠O OO ， 22cos 21211=∠=O OO O O OO ，232112=+=R ，ππ642==R S ；法二：延长1BO 到D 使111r BO DO ==，由余弦定理得6=SB ，2=SD ，大圆直径为62==SB R ；（4）在边长为32的菱形ABCD 中，60=∠BAD ，沿对角线BD 折成二面角C BD A --为120的四面体ABCD ，则此四面体的外接球表面积为 π28解：如图，取BD 的中点M ，ABD ∆和CBD ∆的外接圆半径为221==r r ，ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离（弦心距）为121==d d ，法一：四边形21MO OO 的外接圆直径2=OM ，7=R ，π28=S ；法二：31=OO ，7=R ；法三：作出CBD ∆的外接圆直径CE ,则3==CM AM ， 4=CE ，1=ME ，7=AE ，33=AC ，72147227167cos -=⋅⋅-+=∠AEC ，7233sin =∠AEC ，72723333sin 2==∠=AEC AC R ，7=R ；(5)在四棱锥ABCD 中， 120=∠BDA ，150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --(4)题图的平面角的大小为120，则此四面体的外接球的体积为解：如图，过两小圆圆心作相应小圆所在平面的垂线确定球心，→抽象化(5)题解答图-2(5)题解答图-11B32=AB ，22=r ，弦心距32=M O ，13=BC ，131=r ，弦心距321=M O ，∴2121=O O ，72120sin 21==O O OM ，法一：∴292222=+==OM MD OD R ，29=R ，∴329116π=球V ；法二：2522222=-=M O OM OO ，∴29222222=+==OO r OD R ，29=R ，∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（）A ．π12125 B ．π9125 C ．π6125 D ．π3125解：（1）52==AC R ，25=R ，6125812534343πππ=⋅==R V ，选C（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCDA -的外接球的表面积为．解：BD 的中点是球心O ，132==BD R ，ππ1342==R S .第四讲多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高；第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高；第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是62a π，解：设正四面体内切球的半径为r ，将正四面体放入棱长为2a的正方体中（即补形为正方体），如图，则 2622313133aa V V ABC P =⋅==-正方体，又 r a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-， ∴263332a r a =，62a r =，∴内切球的表面积为(1)题D图8-1A图8-26422a r S ππ==表（注：还有别的方法，此略）（2）正四棱锥ABCD S -的底面边长为2，侧棱长为37解：如图，正四棱锥ABCD S -的高7=h ，正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ，正四棱锥ABCD S -的表面积为284+=表S ，正四棱锥ABCD S -的体积为r r S V ABCD S ⋅+==-328431表，∴3743284=⋅+r ， 771427)122(7221728474-=-=+=+=r （3）三棱锥ABC P -中，底面ABC ∆是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则32解：如图，3=∆ABC S ，2==∆∆ACP ABP S S ，7=∆BCP S ，743++=表S ，三棱锥ABC P -的体积为332=-ABC P V ，另一表达体积的方式是r r S V ABC P ⋅++==-347331表，∴3323473=⋅++r ，∴47332++=r习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（） A.3 B.6 C.36 D.9 解：【A 】616164)2(2=++=R ，3=R【三棱锥有一侧棱垂直于底面，且底面是直角三角形】【共两种】2．三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 .332π(2)题(3)题B解：260sin 32==r ，16124)2(2=+=R ，42=R ，2=R ，外接球体积332834ππ=⋅ 【外心法（加中垂线）找球心；正弦定理求球小圆半径】3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解：ABC ∆外接圆的半径为，三棱锥ABC S -的直径为3460sin 22== R ，外接球半径32=R ，或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ=⋅==R V ， 4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：PAC ∆的外接圆是大圆，3460sin 22==R ，32=R ， 5．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ，81216)97(1sin 22⋅=-=∠P ，924sin =∠P ，42922992422===R ，829=R 6．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .解：AC 是公共的斜边，AC 的中点是球心O ，球半径为1=R。

玩转外接球、内切球、棱切球(最新人教版优质教案)( 含解析 )

玩转外接球、内切球、棱切球【考点预测】知识点一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．2.长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．(2)若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA 2，如图3所示． (4)若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示图1 图2 图3 图4知识点二:正四面体外接球如图，设正四面体ABCD 的的棱长为a ，将其放入正方体中，则正方体的棱长为22a ，显然正四面体和正方体有相同的外接球．正方体外接球半径为R =22a ⋅32=64a ，即正四面体外接球半径为R =64a ．知识点三:对棱相等的三棱锥外接球四面体ABCD 中，AB =CD =m ，AC =BD =n ，AD =BC =t ，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题．如图，设长方体的长、宽、高分别为a ,b ,c ，则b 2+c 2=m 2a 2+c 2=n 2a 2+b 2=t 2，三式相加可得a 2+b 2+c 2=m 2+n 2+t 22,而显然四面体和长方体有相同的外接球，设外接球半径为R ，则a 2+b 2+c 2=4R 2，所以R =m 2+n 2+t 28．知识点四:直棱柱外接球如图1，图2，图3，直三棱柱内接于球(同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形)图1图2图3第一步：确定球心O的位置，O1是ΔABC的外心，则OO1⊥平面ABC；第二步：算出小圆O1的半径AO1=r，OO1=12AA1=12h(AA1=h也是圆柱的高)；第三步：勾股定理：OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2，解出R知识点五:直棱锥外接球如图，PA⊥平面ABC，求外接球半径．解题步骤：第一步：将ΔABC画在小圆面上，A为小圆直径的一个端点，作小圆的直径AD，连接PD，则PD必过球心O；第二步：O1为ΔABC的外心，所以OO1⊥平面ABC，算出小圆O1的半径O1D=r(三角形的外接圆直径算法：利用正弦定理，得asin A=bsin B=csin C=2r)，OO1=12PA；第三步：利用勾股定理求三棱锥的外接球半径：①(2R)2=PA2+(2r)2⇔2R=PA2+(2r)2；②R2=r2+OO12⇔R=r2+OO12．知识点六:正棱锥与侧棱相等模型1.正棱锥外接球半径：R =r 2+h 22h．2.侧棱相等模型：如图，P 的射影是ΔABC 的外心⇔三棱锥P -ABC 的三条侧棱相等⇔三棱锥P -ABC 的底面ΔABC 在圆锥的底上，顶点P 点也是圆锥的顶点．解题步骤：第一步：确定球心O 的位置，取ΔABC 的外心O 1，则P ,O ,O 1三点共线；第二步：先算出小圆O 1的半径AO 1=r ，再算出棱锥的高PO 1=h (也是圆锥的高)；第三步：勾股定理：OA 2=O 1A 2+O 1O 2⇒R 2=(h -R )2+r 2，解出R =r 2+h 22h．知识点三:侧棱为外接球直径模型方法：找球心，然后作底面的垂线，构造直角三角形．知识点四:共斜边拼接模型如图，在四面体ABCD 中，AB ⊥AD ，CB ⊥CD ，此四面体可以看成是由两个共斜边的直角三角形拼接而形成的，BD 为公共的斜边，故以“共斜边拼接模型”命名之．设点O 为公共斜边BD 的中点，根据直角三角形斜边中线等于斜边的一半的结论可知，OA =OC =OB =OD ，即点O 到A ，B ，C ，D 四点的距离相等，故点O 就是四面体ABCD 外接球的球心，公共的斜边BD 就是外接球的一条直径．知识点五:垂面模型如图1所示为四面体P-ABC，已知平面PAB⊥平面ABC，其外接球问题的步骤如下：(1)找出△PAB和△ABC的外接圆圆心，分别记为O1和O2．(2)分别过O1和O2作平面PAB和平面ABC的垂线，其交点为球心，记为O．(3)过O1作AB的垂线，垂足记为D，连接O2D，则O2D⊥AB．(4)在四棱锥A-DO1OO2中，AD垂直于平面DO1OO2，如图2所示，底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径．图1图2知识点六:最值模型这类问题是综合性问题，方法较多，常见方法有：导数法，基本不等式法，观察法等知识点七:二面角模型如图1所示为四面体P-ABC，已知二面角P-AB-C大小为α，其外接球问题的步骤如下：(1)找出△PAB和△ABC的外接圆圆心，分别记为O1和O2．(2)分别过O1和O2作平面PAB和平面ABC的垂线，其交点为球心，记为O．(3)过O1作AB的垂线，垂足记为D，连接O2D，则O2D⊥AB．(4)在四棱锥A-DO1OO2中，AD垂直于平面DO1OO2，如图2所示，底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径．知识点八:坐标法对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为O(x,y,z)，利用球心到各顶点的距离相等建立方程组，解出球心坐标，从而得到球的半径长．坐标的引入，使外接球问题的求解从繁琐的定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度．知识点九:圆锥圆柱圆台模型1.球内接圆锥如图1，设圆锥的高为h，底面圆半径为r，球的半径为R．通常在△OCB中，由勾股定理建立方程来计算R．如图2，当PC>CB时，球心在圆锥内部；如图3，当PC<CB时，球心在圆锥外部．和本专题前面的内接正四棱锥问题情形相同，图2和图3两种情况建立的方程是一样的，故无需提前判断．由图2、图3可知，OC=h-R或R-h，故(h-R)2+r2=R2，所以R=h2+r2 2h．2.球内接圆柱如图，圆柱的底面圆半径为r，高为h，其外接球的半径为R，三者之间满足h2+r2=R2．3.球内接圆台R2=r22+r22-r21-h22h2，其中r1,r2,h分别为圆台的上底面、下底面、高．知识点四:锥体内切球方法：等体积法，即R=3V体积S表面积知识点五:棱切球方法：找切点，找球心，构造直角三角形【题型归纳目录】题型一：正方体、长方体模型题型二：正四面体模型题型三：对棱相等模型题型四：直棱柱模型题型五：直棱锥模型题型六：正棱锥与侧棱相等模型题型七：侧棱为外接球直径模型题型八：共斜边拼接模型题型九：垂面模型题型十：最值模型题型十一：二面角模型题型十二：坐标法模型题型十三：圆锥圆柱圆台模型题型十四：锥体内切球题型十五：棱切球【典例例题】题型一:题型一：正方体、长方体模型例1.(2022·陕西安康·高二期末(理))长方体的长，宽，高分别为3，2，1，其顶点都在球O的球面上，则球O的体积为( )A.43πB.12πC.48πD.323π【答案】A【解析】球O的半径为32+22+122=3，∴体积V=4π⋅333=43π．故选：A例2.(2022·全国·高一阶段练习)已知三棱锥P-BCD中，BC⊥CD，PB⊥底面BCD，BC=1，PB= CD=2，则该三棱锥的外接球的体积为( )A.74πB.92πC.278πD.259π【答案】B【解析】解：如图所示，将三棱锥P-BCD放在长、宽、高分别为2，1，2的长方体中，则三棱锥P-BCD的外接球即为该长方本的外接球，所以外接球的直径PD=BC2+CD2+PB2=12+22+22=3，∴该球的体积为43π×32 3=92π．故选：B例3.(2022·北京市第三十五中学高一阶段练习)已知正方体外接球的体积是323π，那么正方体的体对角线等于( )A.233B.4C.423D.433．【答案】B【解析】解：正方体外接球的直径即为正方体的体对角线，设外接球的半径为R，则V=43πR3=323π，解得R=2，所以正方体的体对角线等于2R=4；故选：B例4.(2022·黑龙江·勃利县高级中学高一期中)据《九章算术》记载，“鳖臑”为四个面都是直角三角形的三棱锥．如图所示，现有一个“鳖臑”，PA⊥底面ABC，AB⊥BC，且PA=AB=BC=2，三棱锥外接球表面积为( )A.10πB.12πC.14πD.16π【答案】B【解析】如图，将三棱锥补形为正方体，则外接球半径R =PC 2=AP 2+AB 2+BC 22=4+4+42=3．所以三棱锥外接球表面积S =4πR 2=4π×3=12π．故选：B ．例5.(2022·河北·高一期中)《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”．现有一“阳马”P -ABCD ，PA ⊥平面ABCD ，AB =4，△PAD 的面积为4，则该“阳马”外接球的表面积的最小值为( )A.24πB.28πC.32πD.36π【答案】C【解析】如图，将四棱锥P -ABCD 补成长方体，则该四棱锥的外接球与长方体的外接球相同．因为长方体外接球的半径r =42+AD 2+PA 22，所以该“阳马”外接球的表面积为：4π×r 2=AD 2+PA 2+16 π≥(2AD ⋅PA +16)π=4×12AD ⋅PA +16 =4×4+16 π=32π．故选：C ．例6.(2022·河南·模拟预测(文))在三棱锥A -BCD 中，已知AC ⊥平面BCD ，BC ⊥BD ，且AC =3，BC =2，BD =5，则该三棱锥外接球的表面积为( )A.12πB.7πC.9πD.8π【答案】A【解析】由AC ⊥平面BCD ，BC ⊥BD ，知三棱锥A -BCD 可补形为以BD ,BC ，AC 为长宽高的长方体，三棱锥的外接球即长方体的外接球，设外接球的半径为R ，则2R 2=3+4+5=12，所以S 球=4πR 2=12π．故选：A 题型二:正四面体模型例7.(2022·全国·高三专题练习(理))棱长为a 的正方体内有一个棱长为x 的正四面体，且该正四面体可以在正方体内任意转动，则x 的最大值为( )A.12aB.32aC.36aD.63a 【答案】D【解析】棱长为a 的正方体的内切球的半径为a 2，正四面体可以在正方体内任意转动，只需该正四面体为球的内接正四面体，换言之，棱长为x 的正四面体的外接球的半径为a 2，设正四面体为P -ABC ，过P 作PO ⊥平面ABC ，垂足为O ，O 为底面正ΔABC 的中心，则AO =23×32x =33x ，体高为x 2-33x 2=63x ，由于外接球半径为a 2 ，利用勾股定理得：63x -a 2 2+33x2=a 2 2 ，解得x =63a ，选D ．例8.(2022·河南·西平县高级中学模拟预测(理))一个正四面体的棱长为2，则这个正四面体的外接球的体积为( )A.6πB.2πC.3πD.22π【答案】A 【解析】如图，四面体BDMN 是正四面体，棱长BD =2，将其补形成正方体GB CD -MENF ，则正方体GB CD -MENF 的棱长GB =22BD =2，此正方体的体对角线长为6，正四面体BDMN 与正方体GB CD -MENF 有相同的外接球，则正四面体BDMN的外接球半径R =62，所以正四面体BDMN 的外接球体积为V =43πR 3=43π⋅623=6π．故选：A例9.(2022·贵州师大附中高二开学考试(理))已知正四面体的棱长为2，则其外接球的表面积为( )A.4πB.6πC.8πD.10π【答案】B【解析】因为正四面体的棱长为2，所以底面三角形的高3，棱锥的高为h =22-233 2=263，设外接球半径为R ，则R 2=263-R 2+233 2，解得R =62．所以外接球的表面积为S =4πR 2=4π622=6π．故选：B ．例10.(2022·河北·石家庄二中一模(理))如图所示，正四面体ABCD 中，E 是棱AD 的中点，P 是棱AC上一动点，BP +PE 的最小值为14，则该正四面体的外接球表面积是( )A.12πB.32πC.8πD.24π【答案】A【解析】将侧面△ABC 和△ACD 沿AC 边展开成平面图形，如图所示，菱形ABCD ，在菱形ABCD 中，连接BE ，交AC 于点P ，则BE 的长即为BP +PE 的最小值，即BE =14，因为正四面体ABCD ，所以AC =AB ，所以∠BCD =120°，因为E 是棱AD 的中点，所以∠DCE =30°，所以∠BCE =∠BCD -∠DCE =90°，设DE =x ，则AB =BC =CD =AD =2x ，所以CE =3x ，则BE =BC 2+CE 2=7x =14，所以x =2，则正四面体ABCD 的棱长为22，所以正四面体的外接球半径为64×22=3，所以该正四面体外接球的表面积为S =4π3 2=12π，故选：A例11.(2022·贵州·凯里一中高二期末(理))我们将四个面均为正三角形的四面体称为“正四面体”，在正四面体ABCD 中，E ,F 分别为棱AB ,CD 的中点，当EF =2时，四面体ABCD 的外接球的表面积为()A.12πB.4πC.3πD.6π【答案】D【解析】设正四面体的棱长为2a ，则：AF =BF =3a ，在等腰三角形ABF 中，AF =3a ,AE =a ,∴EF =3a 2-a 2=2a ，据此可得：2a =2,a =1，正四面体的棱长为：2a =2，外接球半径为：R =64×2a =62，其表面积为：4πR 2=6π．本题选择D 选项．例12.(2022·全国·高三专题练习)金刚石是碳原子的一种结构晶体，属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元)，即碳原子处在立方体的8个顶点，6个面的中心，此外在立方体的对角线的14处也有4个碳原子，如图所示(绿色球)，碳原子都以共价键结合，原子排列的基本规律是每一个碳原子的周围都有4个按照正四面体分布的碳原子．设金刚石晶胞的棱长为a ，则正四面体SPQR 的棱长为__________；正四面体SPQR 的外接球的体积是__________．【答案】 22a 316πa 3【解析】依题意可知，O 为正四面体SPQR 的中心，如图：连接SO ，延长交平面PQR 于点M ，则M 为△PQR 的中心，所以设SR =x ，MR =23×32x =33x ，因为OR =SO =14ST =14×3a =34a ，所以SM =SR 2-MR 2=x 2-33x 2=63x ，由OM 2+MR 2=OR 2，得(SM -SO )2+MR 2=OR 2，得63x -34a 2+33x 2=34a 2，解得x =22a ，所以正四面体SPQR 的棱长为22a ．依题意可知，正四面体SPQR 的外接球的圆心为O ，半径为34a ，所以正四面体SPQR 的外接球的体积是43π×34a 3=316πa 3．故答案为：22a ；316πa 3．题型三:对棱相等模型例13.(2022•让胡路区校级模拟)在四面体ABCD 中，若AB =CD =3，AC =BD =2，AD =BC =5，则四面体ABCD 的外接球的表面积为( )A.2πB.4πC.6πD.8π【解析】解：如下图所示，将四面体ABCD 放在长方体AEBF -GCHD 内，设该长方体的长、宽、高分别为x 、y 、z ，则长方体的体对角线长即为长方体的外接球直径，设该长方体的外接球半径为R ，由勾股定理得AB2=x2+y2=3 AC2=x2+z2=4 AD2=y2+z2=5 ，上述三个等式全加得2(x2+y2+z2)=12，所以，该四面体的外接球直径为2R=x2+y2+z2=6，因此，四面体ABCD的外接球的表面积为4πR2=π×(2R)2=6π，故选：C．例14.已知四面体ABCD中，AB=CD=5，BC=AD=10，AC=BD=13，若该四面体的各个顶点都在同一球面上，则此球的表面积为( )A.42πB.43πC.14πD.16π【解析】解：由题意，四面体扩充为长方体，且面上的对角线分别为5，10，13，∴长方体的对角线长为5+10+132=14，∴球的半径为142，∴此球的表面积为4π∙144=14π．故选：C．例15.如图，在三棱锥P-ABC中，PA=BC=3，PB=AC=2，PC=AB=5，则三棱锥P-ABC 外接球的体积为( )A.2πB.3πC.6πD.6π【解析】解：由题意，PA=BC=3，PB=AC=2，PC=AB=5，将三棱锥P-ABC放到长方体中，可得长方体的三条对角线分别为3，2，5，即a2+b2=3，a2+c2=2，c2+b2=5，解得：a=1，b=2，c=3．外接球的半径R=12×a2+b2+c2=62．∴三棱锥P-ABC外接球的体积V=43πR3=6π．故选：C．例16.(2022•永安市校级期中)在三棱锥P-ABC中，PA=BC=4，PB=AC=5，PC=AB=11，则三棱锥P-ABC的外接球的表面积为( )A.26πB.12πC.8πD.24π【解析】解：∵三棱锥P -ABC 中，PA =BC =4，PB =AC =5，PC =AB =11，∴构造长方体，使得面上的对角线长分别为4，5，11，则长方体的对角线长等于三棱锥P -ABC 外接球的直径．设长方体的棱长分别为x ，y ，z ，则x 2+y 2=16，y 2+z 2=25，x 2+z 2=11，∴x 2+y 2+z 2=26，∴三棱锥P -ABC 外接球的直径为26，∴三棱锥P -ABC 外接球的表面积为4π2622=26π．故选：A ．例17.(2022•罗湖区月考)已知在四面体ABCD 中，AB =CD =22,AD =AC =BC =BD =5，则四面体ABCD 的外接球表面积为．【解析】解：如下图所示，将四面体ABCD 放在长方体AEBF -GCHD 内，在四面体ABCD 中，AB =CD =22,AD =AC =BC =BD =5，设该长方体的长、宽、高分别为2、2、1，则长方体的体对角线长即为长方体的外接球直径，设该长方体的外接球半径为R ，所以，该四面体的外接球直径为2R =22+22+12=3，因此，四面体ABCD 的外接球的表面积为4πR 2=π×(2R )2=9π，故答案为：9π．例18.(2022•三模拟)在四面体ABCD 中，AC =BD =2，AD =BC =5，AB =CD =7，则其外接球的表面积为．【解析】解：如下图所示，将四面体ABCD 放在长方体AEBF -GCHD 内，设该长方体的长、宽、高分别为x、y 、z ，则长方体的体对角线长即为长方体的外接球直径，设该长方体的外接球半径为R ，由勾股定理得x 2+y 2=4y 2+z 2=5z 2+x 2=7，上述三个等式全加得2(x 2+y 2+z 2)=16，所以，该四面体的外接球直径为2R =x 2+y 2+z 2=22，因此，四面体ABCD 的外接球的表面积为4πR 2=π×(2R )2=8π，故答案为：8π．题型四:直棱柱模型例19.(2022·山西·太原五中高一阶段练习)在直三棱柱ABC -A 1B 1C 1中，若AB ⊥BC ,AB =6,BC =8,AA 1=6，则该直三棱柱外接球的表面积为( )A.72πB.114πC.136πD.144π【答案】C【解析】由题意可得三棱柱的上下底面为直角三角形，取直角三角形斜边的中点O 1,O 2，直三棱柱ABC -A 1B 1C 1的外接球的球心O 为上下底面的外接圆圆心的连线O 1O 2的中点，连接AO ，AB ⊥BC ,AB =6,BC =8,AC =10，设外接球的半径为R ，下底面外接圆的半径为r ，r =AO 2=5，则R 2=25+9=34，该直三棱柱外接球的表面积为4πR 2=136π，故选：C 例20.(2022·安徽·合肥市第六中学高一期中)设直三棱柱ABC -A 1B 1C 1的所有顶点都在一个球面上，AB =AC =AA 1，∠BAC =120°，且底面△ABC 的面积为23，则此直三棱柱外接球的表面积是( )A.16πB.4010π3C.40πD.64π【答案】C 【解析】设AB =AC =AA 1=m ，因为∠BAC =120°，所以12×m ×m ×sin120°=23，m =22，而∠ACB =30°，所以22sin30°=2r (r 于是是△ABC 外接圆的半径)，r =22，即AM =22，如图，设M ,N 分别是△ABC 和△A 1B 1C 1的外接圆圆心，由直棱柱的性质知MN 的中点O 是三棱柱ABC -A 1B 1C 1的外接球球心，OM =12MN =12AA 1=2，所以外接球为R =OA =AM 2+OM 2=22 2+2 2=10．于是球的表面积为S =4πR 2=4π10 2=40π．故选：C ．例21.(2022·河南·高三阶段练习(文))已知正六棱柱ABCDEF-A1B1C1D1E1F1的每个顶点都在球O的球面上，且AB=3，AA1=4，则球O的表面积为( )A.42πB.48πC.50πD.52π【答案】D【解析】因为AB=3，所以正六边形ABCDEF外接圆的半径r=3，所以球O的半径R=r2+AA122=13，故球O的表面积为4πR2=52π．故选：D例22.(2022·全国·高二课时练习)表面积为81π的球，其内接正四棱柱(底面是正方形的直棱柱)的高是7，则这个正四棱柱的底面边长为______．【答案】4【解析】由题意知：正四棱柱的体对角线即为球的直径，设球的半径为R，则4πR2=81π，解得R=9 2，设正四棱柱的底面边长为a，则a2+a2+72=2R，解得a=4．故答案为：4．例23.(2022·河南·高三阶段练习(理))已知正三棱柱ABC-A1B1C1的外接球表面积为40π，则正三棱柱ABC-A1B1C1的所有棱长之和的最大值为______．【答案】1210【解析】由已知可得正三棱柱的外接球的球心为上下底面中心连线的中点，由外接球的表面积求出外接球半径，由底面边长求出底面外接圆半径，求出球心到底面的距离，进而求出正三棱柱的高，即可求出结论，【详解】设正三棱柱上下底面中心分别为H,H1，连HH1，取HH1中点O为正三棱柱外接球的球心，连OA为外接球的半径，如图，∴4π×OA2=40π，∴OA=10设正三棱柱ABC-A1B1C1的底面边长为x，∴AH=23×32x=33x，在RtΔAOH中，OH=OA2-AH2=10-13x2，∴HH1=210-13x2三棱柱ABC-A1B1C1的所有棱长之和为l=6x+610-13x2(0<x<30)．l =61-x 310-13x 2 ,(0<x <30)，令l =0，解得x =3102，当0<x <3102时，l >0，当3102<x <30时，l <0，所以x =3102是函数在定义域内有唯一极大值点，故当x =3102时，l =6x +610-13x 2(0<x <30)有最大值1210．故答案为： 1210．例24.(2022·浙江·高二期中)在直三棱柱ABC -A 1B 1C 1中，∠BAC =90°且BB 1=4，已知该三棱柱的体积为2，则此三棱柱外接球表面积的最小值为______．【答案】18π【解析】设BC 的中点为D ，B 1C 1的中点为D 1，AB =x ,AC =y ，由题，得三棱柱外接球的球心在线段DD 1的中点O 处，由三棱柱的体积为2，得12xy ×4=2，即xy =1，由题，得R 2=OB 2=OD 2+BD 2=4+14x 2+y 2 ，所以，外接球表面积S =4πR 2=4π⋅4+14x 2+y 2 =16π+x 2+y 2 π≥16π+2xy π=18π．故答案为：18π题型五:直棱锥模型例25.(2022·青海·海东市第一中学模拟预测(理))已知四棱锥P -ABCD 中，PA ⊥平面ABCD ，底面ABCD 是矩形，AD =3AB =3PA ，若四棱锥P -ABCD 外接球的表面积为11π，则四棱锥P -ABCD 的体积为( )A.3B.2C.2D.1【答案】D【解析】设四棱锥P -ABCD 外接球的半径为R ，则4πR 2=11π，即4R 2=11．由题意，易知PC 2=4R 2，得PC =11，设AB =x ，得x 2+9x 2+x 2=11，解得x =1，所以四棱锥P -ABCD 的体积为13×1×3×1=1．故选：D 例26.(2022·全国·高三专题练习)《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥M -ABC 为鳖臑，MA ⊥平面ABC ，AB ⊥BC ，AB =BC =2，MA =4，三棱锥M -ABC 的四个顶点都在球O 的球面上，则球O 的表面积为( )A.9πB.16πC.20πD.24π【答案】D【解析】如图所示，作AC 边上的中点D ，MC 边上的中点O ，连接ODMA ⊥平面ABC ，可得：MA ⊥AC ，OD ⊥AC可得：O 为球O 的球心，OC 为球的半径在直角三角形△ABC 中，可得：AC =22在直角三角形△ODC 中，可得：OC =6故球的表面积为：4π6 2=24π故选：D 例27.(2022·广西·宾阳中学高一阶段练习)已知三棱锥S -ABC 中，SA ⊥平面ABC ，AB =BC =CA=33，三棱锥S -ABC 外接球O 的表面积为100π，则球O 的体积为_______，异面直线SA ，OB 所成角的余弦值为________．【答案】 5003π；45【解析】由外接球表面积可知S =4πR 2=100π，解得R =5，所以球的体积V =43πR 3=5003π，如图，设球心为O ，H 为SA 中点，G 为△ABC 中心，连接OB ，OG ，因为G 为△ABC 中心，球心为O ，所以OG ⊥平面ABC ，又SA ⊥平面ABC ，所以OG ⎳SA ，由OG ⎳SA 可知，异面直线SA ，OB 所成角为∠BOG ，在Rt △ABC 中，cos ∠BOG =OG OB=R 2-BG 2R=25-23×32×33 25=45，故答案为：5003π；45．例28.(2022·河南·新乡市第一中学高一期末)已知三棱锥S -ABC 中，SA ⊥平面ABC ，SA =4，BC =23，∠BAC =60∘，则三棱锥S -ABC 外接球的表面积为______．【答案】32π【解析】如下图所示：圆柱O 1O 2的底面圆直径为2r ，母线长为h ，则O 1O 2的中点O 到圆柱底面圆上每点的距离都相等，则O 为圆柱O1O 2的外接球球心，球O 的半径为R =r 2+h 2 2，可将三棱锥S -ABC 置于圆柱O 1O 2内，使得圆O 2为△ABC 的外接圆，如下图所示：由正弦定理可知圆O 2的直径为2r =BC sin60∘=4，所以，三棱锥S -ABC 外接球的半径R =SA 2 2+r 2=22，因此，三棱锥S -ABC 外接球的表面积为4πR 2=32π．故答案为：32π．例29.(2022·青海·海东市第一中学模拟预测(文))已知在三棱锥P -ABC 中，PA =4，BC =26，PB =PC =3，PA ⊥平面PBC ，则三棱锥P -ABC 的外接球的表面积是( )A.43πB.42πC.48πD.46π【答案】A【解析】在△PBC 中，由余弦定理得：cos ∠BPC =PB 2+PC 2-BC 22PB ⋅PC =-618=-13，∴sin ∠BPC =1-cos 2∠BPC =223，∴△BPC 外接圆半径r =12×BC sin ∠BPC =12×26223=332，又PA ⊥平面PBC ，∴三棱锥P -ABC 的外接球半径R =r 2+12PA 2=274+4=432，则三棱锥P -ABC 的外接球的表面积S =4πR 2=43π．故选：A ．例30.(2022·全国·高一阶段练习)已知三棱锥P -BCD 中，BC ⊥CD ，PB ⊥底面BCD ，BC =1，PB =CD =2，则该三棱锥的外接球的体积为( )A.74π B.92πC.278π D.259π【答案】B【解析】解：如图所示，将三棱锥P -BCD 放在长、宽、高分别为2，1，2的长方体中，则三棱锥P -BCD 的外接球即为该长方本的外接球，所以外接球的直径PD =BC 2+CD 2+PB 2=12+22+22=3，∴该球的体积为43π×32 3=92π．故选：B 例31.(2022·河北沧州·高一期末)已知在三棱锥A -BCD 中，AB ⊥平面BCD ，AB =23,AC =AD =4,CD =2，则三棱锥A -BCD 外接球的表面积为( )A.40π3B.15πC.52π3D.20π【答案】C【解析】因AB ⊥平面BCD ，BC ,BD ⊂平面BCD ，则AB ⊥BC ,AB ⊥BD ，而AB=23,AC =AD =4，则BC =BD =2=CD ，三棱锥A -BCD 的外接球O 截平面BCD 所得小圆圆心O 1是正△BCD 的中心，O 1B =233，连OO 1，则OO 1⊥平面BCD ，取线段AB 的中点E ，则球O 的球心O 在过E 垂直于直线AB 的垂面上，连OE ，如图，则四边形BEOO 1是矩形，OO 1=BE =12AB =3，因此，球O 的半径BO 有：BO 2=BO 21+OO 21=133，所以三棱锥A -BCD 外接球的表面积S =4π⋅BO 2=52π3．故选：C题型六:正棱锥与侧棱相等模型例32.(2022·江西·高三阶段练习(文))在正三棱锥P -ABC 中，PA ⊥PB ，P 到平面ABC 的距离为2，则该三棱锥外接球的表面积为( )A.36πB.16πC.16π3D.4π【答案】A【解析】因为PA ⊥PB ，由正三棱锥的性质知，PA ，PB ，PC 两两垂直且相等．设PA =PB =PC =a ，则AB =BC =CA =2a ．根据V P -ABC =V A -PBC ，得13×12×a 2×a =13×12×2a 2sin60°×2，解得a =23．设三棱锥P -ABC 外接球的半径为R ，则2R =PA 2+PB 2+PC 2=36=6，所以R =3．故所求外接球的表面积为36π．故选：A ．例33.(2022·江苏·高一课时练习)如图在正三棱锥S -ABC 中，M ,N 分别是棱SC ,BC 的中点，Q 为棱AC 上的一点，且AQ =12QC ，MN ⊥MQ ，若AB =22，则此正三棱锥S -ABC 的外接球的体积为( )A.12πB.433πC.83πD.43π【答案】D 【解析】因为在△SBC 中，M ,N 分别是棱SC ,BC 的中点，所以MN ⎳SB ，因为MN ⊥MQ ，所以SB ⊥MQ ，因为三棱锥S -ABC 为正三棱锥，所以SB ⊥AC (对棱垂直)，又因为MQ ,AC ⊂面SAC ，MQ ∩AC =Q ，所以SB ⊥面SAC ，因为SA ,SC ⊂面SAC ，所以SB ⊥SA ,SB ⊥SC ，在Rt △SAB 中，SA 2+SB 2=AB 2，因为三棱锥S -ABC 为正三棱锥，所以△SBC 是等腰三角形，△ABC 是等边三角形，所以SB =SC ，AB =AC ，所以SA 2+SC 2=AC 2，即SA ⊥SC ，所以SA ,SB ,SC 两两垂直，将此三棱锥放入正方体中，此正方体的面对角线长等于AB 长，为22，则该正方体棱长为2，外接球半径R =22 2+222 2=3，正方体外接球体积V =43πR 3=43π×3 3=43π，此正三棱锥S -ABC 的外接球体积和正方体外接球体积相同，为43π．故选：D例34.(2022·重庆市实验中学高一阶段练习)三棱锥P -ABC 体积为36，且PA =PB =PC ,AB =AC =1,BC =3，则三棱锥外接球的表面积为____________．【答案】254π【解析】三棱锥P -ABC 中，取BC 中点D ，连PD ，连AD 并延长至O 1，使DO 1=AD ，连接BO 1，CO 1，PO 1，如图：于是得四边形ABO 1C 为平行四边形，而AB =AC =1，▱ABO 1C 是菱形，在△ABC 中，BC =3，由余弦定理有cos ∠BAC =AB 2+AC 2-BC 22AB ⋅AC =-12，即∠BAC =120∘，则∠ABO 1=60∘，△ABO 1是正三角形，O 1A =O 1B =O 1C =1，于是得O 1是△ABC 外接圆圆心，因PA =PB =PC ，D 为BC 中点，则PD ⊥BC ，又AO 1⊥BC ，PD ∩AO 1=D ，PD ,AO 1⊂平面PAO 1，从而有BC ⊥平面PAO 1，PO 1⊥BC ，同理PO 1⊥AC ，而AC ∩BC =C ，从而得PO 1⊥平面ABC ，由球的截面小圆性质知，三棱锥P -ABC 外接球球心O 在直线PO 1上，又S △ABC =12AB ⋅AC sin120∘=34，则V P -ABC =13PO 1⋅S △ABC =36，解得PO 1=2，设球O 的半径为R ，则OB =OP =R ，OO 1=|R -2|，Rt △OO 1B 中，O 1B 2+O 1O 2=OB 2，即1+(R -2)2=R 2，解得R =54，则球O 的表面积为S =4πR 2=25π4，所以三棱锥外接球的表面积为254π．故答案为：254π例35.(2022·重庆·高二期末)如图，在三棱锥A -BCD 中，AB =AC =BC =BD =CD ，二面角A -BC-D 的余弦值为-13，若三棱锥A -BCD 的体积为13，则三棱锥A -BCD 外接球的表面积为______．【答案】4π【解析】取BC 的中点E ，连接AE ，DE ，过点A 作AH ⊥DE ，交DE 的延长线于点H ，所以∠AED 为二面角A -BC -D 的平面角，设AB =2a ，则AE =DE =3a ，cos ∠AED =-13，所以sin ∠AEH =sin ∠AED =223，所以AH =263a ，EH =13AE =33a ，因为三棱锥A -BCD 的体积为13，所以13×34×(2a )2×263a =13，解得：a =22，EH =66，设△BCD 外接圆的圆心为O '，三棱锥A -BCD 外接球的球心为O ，连接OO ，OC ，O C ，过点O 作OF ⊥AH 于点F ，则O 'C =O 'D =23DE =63，O E =13DE =66，O H =OF ，OA =OC ，设OO =FH =h ，则AF =AH -FH =233-h ，OF =O H =O E +EH =63，由勾股定理得：h 2+632=233-h 2+63 2，解得：h =33，所以三棱锥A -BCD 外接球的半径R 满足R 2=O 'O 2+O 'C 2=1，则三棱锥A -BCD 的外接球的表面积为4πR 2=4π．故答案为：4π．例36.(2022·全国·高一期末)在正三棱锥P -ABC 中，AB =23，正三棱锥P -ABC 的体积是43，则正三棱锥P -ABC 外接球的表面积是( )A.5πB.15πC.25πD.35π【答案】C【解析】如图所示，设点G 为△ABC 的外心，则PG ⊥平面ABC ，由V P -ABC =13S △ABC ⋅PG =13×12×23×23×32⋅PG =43，∴PG =4，则三棱锥P -ABC 的外接球的球心O 在直线PG 上．设其外接球的半径为R ，由正弦定理得AG =AB2sin π3=2，在Rt △OAG 中，OG =|PG -R |=|4-R |，由勾股定理得OA 2=OG 2+AG 2，即R 2=22+|4-R |2，解得R =52．正三棱锥P -ABC 外接球的表面积是S =4πR 2=4π×52 2=25π，故选：C ．例37.(2022·天津市咸水沽第一中学模拟预测)已知正三棱锥S -ABC 的三条侧棱两两垂直，且侧棱长为1，则此三棱锥的外接球的表面积为( )A.πB.3πC.6πD.9π【答案】B【解析】由题意，正三棱锥S -ABC 的三条侧棱两两垂直，且侧棱长为1，此三棱锥S -ABC 可补形为一个棱长为1的正方体，三棱锥S -ABC 的外接球与补成的棱长为1的正方体的外接球为同一个球，设正方体的外接球的半径为R ，可得2R =3，即R =32，所以此三棱锥的外接球的表面积为S =4πR 2=4π×322=3π．故选：B ．例38.(2022·河南安阳·高二阶段练习(理))如图，在三棱锥A -BCD 中，AB =BC =AC =CD =2，∠BCD =120°，二面角A -BC -D 的大小为120°，则三棱锥A -BCD 的外接球的表面积为( )A.82π3B.80π3C.27πD.244π9【答案】D【解析】如图1，过D 作DM ⊥BC 垂足为M ，取BC 的中点E ，连接AE ,CM AE =DM =3,CM =1,BD =23过M 作MN ∥AE ，且MN =AE ，连接AN ，则AN =2∵△ABC 为等边三角形，则AE ⊥BC∴MN ⊥BC ，DM ⊥BC ，根据题意可得∠DMN =2π3∵DN 2=MN 2+DM 2-2MN ⋅DM ⋅cos ∠DMN =9，则DN =3由题意可得AN ⊥DN ，则AD 2=AN 2+DN 2=13，则AD =13如图2，∵AC =BC =CD ，则顶点C 在平面ABD 的投影为△ABD 的外接圆圆心O 1，则三棱锥A -BCD 的外接球的球心O 在直线CO 1上，连接O 1A ,O 1C ,OA cos ∠ABD =AB 2+BD 2-AD 22AB ⋅BD =38，则sin ∠ABD =618∴△ABD 的外接圆半径AO 1=12AD sin ∠ABD =41361，则CO 1=CA 2-AO 12=661设棱锥A -BCD 的外接球的半径为R ，则OA 2=AO 12+OO 12即R 2=413612+661-R 2，解得R =613三棱锥A -BCD 的外接球的表面积为S =4πR 2=244π9故选：D ．例39.(2022·江苏南通·高三期末)已知正四棱锥P -ABCD 的底面边长为22，侧棱PA 与底面ABCD所成的角为45°，顶点P ，A ，B ，C ，D 在球O 的球面上，则球O 的体积是( )A.16πB.323π C.8π D.823π【答案】B【解析】在正四棱锥P -ABCD 中，连接AC ，BD ，AC ∩BD =O ，连PO ，如图，则有PO ⊥平面ABCD ，∠PAO 为侧棱PA 与底面ABCD 所成的角，即∠PAO =45∘，于是得O P =O A =O B =O C =O D =22AB =2，因此，顶点P ，A ，B ，C ，D 在以O 为球心，2为半径的球面上，即点O 与O 重合，所以球O 的体积是V =43π×23=323π．故选：B例40.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3≤l ≤33，则该正四棱锥体积的取值范围是( )A.18,814B.274,814C.274,643D.[18,27]【答案】C【解析】∵ 球的体积为36π，所以球的半径R =3，设正四棱锥的底面边长为2a ，高为h ，则l 2=2a 2+h 2，32=2a 2+(3-h )2，所以6h =l 2，2a 2=l 2-h 2所以正四棱锥的体积V =13Sh =13×4a 2×h =23×l 2-l 436 ×l 26=19l 4-l 636 ，所以V=194l 3-l 56 =19l 324-l 26，当3≤l ≤26时，V >0，当26<l ≤33时，V <0，所以当l =26时，正四棱锥的体积V 取最大值，最大值为643，又l =3时，V =274，l =33时，V =814，所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是274，643．故选：C ．题型七:侧棱为外接球直径模型例41.(2022•五华区校级期末)已知三棱锥P -ABC 的所有顶点都在球O 的球面上，AB =5，AC =3，BC =4，PB 为球O 的直径，PB =10，则这个三棱锥的体积为( )A.303B.153C.103D.53【解析】解：如图所示，由条件ΔABC 为直角三角形，则斜边AB 的中点O 1为ΔABC的外接圆的圆心，连接OO 1得OO 1⊥平面ABC ，OO 1=BO 2-BO 12=523，∵OO 1⎳PA ，PA =2OO 1=53，∴PA ⊥平面ABC ，∴三棱锥的体积为13×12×3×4×53=103．故选：C ．例42.(2022•红花岗区校级月考)已知三棱锥A -BCD 的所有顶点都在同一个球面上，ΔBCD 是边长为。

外接球、内切球模型总结专题课件-高三数学二轮复习备考课件

∴正三棱锥 − 的三条侧棱两两互相垂直
把三棱锥补形为正方体，则正方体外接球即为三棱锥的外接球
其直径为 =

=
1
2 + 2 + 2 + 2 + 2 + 2
2
=
1
2 + 2 + 2 =
2

1

2 + 2 + 2
半径为
6
2
4
球 = ×

找三条两两垂直的线段，直接用公式 2
即2 = 2 + 2 + 2 ，求出

2

= 2 + 2 + 2 ，

例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的
表面积是( C )
B. 20
A.16
C. 24
D. 32
= 2 ℎ = 16
则该四面体的外接球的表面积为( D )
A. 11
B. 7

1

C.
10

3
D.
40

3
在
��
2 = 2 + 2 − 2 ⋅ ⋅ cos120∘

=7
= 7
中
的外接球直径为
7 2 7

=
2 =
=
sin∠
3
3
2
∵ ⊥平面 ∴ ⊥ ∴ ∆是直角三角形
是这个球的外切多面体，这个球是这个多面体的内切球.

几何体的内切球和外接球-三视图-教师版讲义

专题：几何体的内切球和外接球三视图[学习目标]1.掌握几何体的内切球和外接球问题；2.掌握几何体的三视图.※自主研读学习单※1.如果一个球与几何体的各个面都相切,球为几何体的内切球；2.如果一个几何体的所有顶点都在球面上,球为几何体的外接球；3.棱长为a 的正四面体的高为________;它的外接球半径R 为________;内切球半径为________;球心为高的_____等分点.解：如图所示,设点O 是内切球的球心,正四面体棱长为a ．由图形的对称性知,点O 也是外接球的球心．设内切球半径为r ,外接球半径为R ．正四面体的表面积223434a a S =⨯=表．正四面体的体积22221234331BE AB a AE a V BCD A -=⨯⨯=- BCD A V r S -=⋅表31 ,a aa S V r BCD A 12631223323=⨯==∴-表在BEO Rt ∆中,222EO BE BO +=,即22233r a R +⎪⎪⎭⎫ ⎝⎛=,得a R 46=,得r R 3= 变式：一个正四面体内切球的表面积为π3,求正四面体的棱长.〔答案为：32〕4.正方体的内切球2a R =： 5.与正方体各棱相切的球：球与正方体的各棱相切,切点为各棱的中点,a R 22=6.正方体的外接球：正方体的八个顶点都在球面上,a O A R 231==. 变式：一棱长为a 2的框架型正方体,内放一能充气吹胀的气球,求当球与正方体棱适好接触但又不至于变形时的球的体积.〔答案为()33482233V a a ππ==〕 7.正棱柱的外接球,其球心定在上下底面中心连线的中点处,由球心、底面中心与底面一顶点构成的直角三角形便可得球半径.※合作探究学习单※题型一几何体的内切球和外接球例1.正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切．求球的表面积与体积．解：如图,球O 是正三棱锥ABC P -的内切球,O 到正三棱锥四个面的距离都是球的半径R ． PH 是正三棱锥的高,即1=PH ．E 是BC 边中点,H 在AE 上,ABC ∆的边长为62,∴26263=⨯=HE ．∴3=PE 可以得到2321=⋅===∆∆∆PE BC S S S PBC PAC PAB ．36)62(432==∆ABC S 由等体积法,ABC O PBC O PAC O PAB O ABC P V V V V V -----+++=∴R R ⨯⨯+⨯⨯⨯=⨯⨯36313233113631得：2633232-=+=R , ∴πππ)625(8)26(4422-=-==R S 球．∴33)26(3434-==ππR V 球．例2.求球与它的外切圆柱、外切等边圆锥的体积之比．分析：首先画出球与它的外切圆柱、等边圆锥,它们公共的轴截面,然后寻找几何体与几何体之间元素的关系．解：如图,等边SAB ∆为圆锥的轴截面,此截面截圆柱得正方形11CDD C ,截球面得球的大圆圆1O ．设球的半径R OO =1,则它的外切圆柱的高为R 2,底面半径为R ；R O O OB 330cot 1=︒⋅=,R R OB SO 33360tan =⋅=︒⋅=,∴334R V π=球,3222R R R V ππ=⋅=柱,3233)3(31R R R V ππ=⋅⋅=锥, ∴964∶∶∶∶锥柱球=V V V ．例3.已知正三棱柱111C B A ABC -的六个顶点在球1O 上,又知球2O 与此正三棱柱的5个面都相切,求球1O 与球2O 的体积之比与表面积之比.分析：先画出过球心的截面图,再来探求半径之间的关系.解：如图,由题意得两球心1O 、2O 是重合的,过正三棱柱的一条侧棱1AA 和它们的球心作截面,设正三棱柱底面边长为a ,则a R 632=, 正三棱柱的高为a R h 3322==,由O D A Rt 11∆中,得 22222221125633333a a a R a R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛=,a R 1251=∴ 1:5::222121==∴R R S S ,1:55:21=V V例4.设棱锥ABCD M -的底面是正方形,且MD MA =,AB MA ⊥,如果AMD ∆的面积为1,试求能够放入这个棱锥的最大球的半径.解：⊥∴⊥⊥AB MA AB AD AB ,, 平面MAD ,由此,面⊥MAD 面AC .记E 是AD 的中点,从而AD ME ⊥.⊥∴ME 平面AC ,EF ME ⊥设球O 是与平面MAD 、平面AC 、平面MBC 都相切的球.如图2,得截面图MEF ∆与内切圆O不妨设∈O 平面MEF ,于是O 是MEF ∆的内心.设球O 的半径为r ,则MFEM EF S r MEF ++=∆2,设a EF AD ==,1=∆AMD S . 222,2⎪⎭⎫ ⎝⎛+==∴a a MF a EM ,12222222222-=+≤⎪⎭⎫ ⎝⎛+++=a a a a r当且仅当aa 2=,即2=a 时,等号成立. ∴当2==ME AD 时,满足条件的球最大半径为12-.例5.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解设矩形对角线的交点为O ,则由矩形对角线互相平分,可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,∴外接球的半径52R OA ==.故3412536V R ππ==球.选C. 题型二几何体的三视图三视图常考查：①三视图的识别与还原问题；②以三视图为载体考查空间几何体的表面积、体积等问题．主要考查学生的空间想象能力与运算能力,是近几年高考的热点．例1.已知某个几何体的三视图如图,根据图中标出的尺寸<单位：cm>,可得这个几何体的体积是<>．A.错误! cm 3B.错误! cm 3C ．2 000 cm 3D ．4 000 cm 3[审题视点] 画出直观图后求解．[此几何体的图为SABCD ,且平面SCD ⊥平面ABCD ,ABCD 为正方形,边长为20 c m ,S 在底面的射影为CD 的中点E ,SE ＝20 c m ,V SABCD ＝错误!S ▱ABCD ·SE ＝错误! c m 3.故选B.]解答此类题目时：<1>可以从熟知的某一视图出发,想象出直观图,再验证其他视图是否正确；<2>视图中标注的长度在直观图中代表什么,要分辨清楚；<3>视图之间的数量关系：正俯长对正,正侧高平齐,侧俯宽相等．例2.如图是某三棱柱被削去一个底面后的直观图与侧<左>视图、俯视图．已知CF ＝2AD ,侧<左>视图是边长为2的等边三角形；俯视图是直角梯形,有关数据如图所示．求该几何体的体积．解如图,取CF 的中点P ,过P 作PQ ∥CB 交BE 于Q ,连接PD ,QD ,AD ∥CP ,且AD ＝CP .四边形ACPD 为平行四边形,∴AC ∥PD .∴平面PDQ ∥平面ABC ,该几何体可分割成三棱柱PDQCAB 和四棱锥DPQEF ,∴V ＝V 三棱柱PDQCAB ＋V DPQEF ＝错误!×22si n 60°×2＋错误!×错误!×错误!＝3错误!.例3.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .62B .42C .6D .4答案：B[课堂小结]几何体的内切球和外接球三视图※巩固提升学习单※1．若一个正三棱柱存在外接球与内切球,则它的外接球与内切球表面积之比为〔〕A. 3 ：1 B . 4 ：1 C . 5 ：1 D. 6 ：1[答案]C[解析]设内切球的半径为r,外接球的半径为R,底边边长为a,则222233315,()()6336a r R r a r a a ==+=+=,所以225S R S r==外接球内切球 2．在正四棱锥S -ABCD 中,侧面与底面所成的角为3π,则它的外接球半径R 与内切球半径r 之比为〔〕 A ．5B ．32C ．10D ．52[答案]D3．已知四面体ABCD 中,AB ＝AD ＝6,AC ＝4,CD ＝13⊥平面ACD,则四面体 ABCD 外接球的表面积为〔〕A ．36πB ．88πC ．92πD ．128π[答案]B[解析]试题分析：在ACD ∆中,由64213AD AC CD ＝，＝，＝,可得222AD AC CD +=,则AC AD ⊥,又AB ACD ⊥平面,故222246688222R =++==,则24(22)88V ππ==.4．一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积．．．为_________.[解析]由三视图可得,该几何体为一条侧棱垂直于底面的四棱锥,如下图中1C ABCD -,其中底面ABCD 为边长为1的正方形,11C C =由图可知,该四棱锥的外接球球心即该四棱锥所在的正方体的中心,由此可得球半径32R =,所以其表面积为243S R ππ== 5．在正三棱锥S -ABC 中,M 、N 分别是SC 、BC 的中点,且,若侧棱SA=,则正三棱锥 S -ABC 外接球的表面积为______________.[解析]如图,因为,M N 分别是,SC BC 中点,所以//MN SB .而S ABC -是正三棱锥,所以SB AC ⊥,所以MN AC ⊥.因为MN AM ⊥,所以MN ⊥面SAC ,从而可得SB ⊥面SAC ,故90BSA BSC ASB ∠=∠=∠=.将此正三棱锥补成正方体,则它们有相同的外接球.因为侧棱23SA =,所以补成的正方体的边长为23,则它们的外接球半径32332R =⋅=,所以外接球表面积为2436S R ππ==6．已知四面体ABC P -的外接球的球心O 在AB 上,且⊥PO 平面ABC ,AB AC 32=,若四面体AM MN ⊥32正视图侧视图俯视图ABC P -的体积为23,则该球的体积为___________； [答案]π34[解析] 试题分析：设球的半径为R ,因为球心O 在AB 上,所以O 为AB 的中点,且ABC ∆为直角三角形,因为AB AC 32=,所以2AC AB ==,BC R =,所以31113,3322P ABC ABC V S OP R R R -∆=⨯⨯=⨯⨯⨯=∴=所以该球的体积为34.3R π= 考点：本小题主要考查四面体的内接球的体积计算.点评：解决此小题的关键是分析出ABC ∆是直角三角形,考查学生的空间想象能力和运算求解能力.7．在平行四边ABCD 中,90ABD ∠=︒,2224AB BD +=,若将其沿BD 折成直二面角 A -BD -C,则三棱锥A—BCD 的外接球的体积为_______.[答案]43π [解析]试题分析：因为球心到各定点的距离相等,所以易知该外接球的球心在AC 的中点,又在平行四边ABCD 中,90ABD ∠=︒,所以2222244AB BD AD AB +=⇒+=,而折成直二面角后,222224,2AC AD CD AD AB AC =+=+=∴=,所以该外接球的球半径为1,所以体积为4.3π 考点：本小题主要考查空间几何体的外接球的体积.点评：对于这种折叠问题,要搞清楚折叠前后的量有哪些发生了变化,哪些没有发生变化.8．如图是一个空间几何体的三视图,则该几何体的外接球的表面积为.[答案]8π[解析]试题分析：由三视图可知空间几何体为三棱锥,底面为直角三角形,侧棱垂直于底面,设底面为,90ABC B ∠=,侧棱,SA AB SA AC ⊥⊥所以其外接球球心在SC 中点处,球的半径r =所以表面积248S r ππ==考点：三视图与球的表面积计算点评：先由三视图还原直观图在求其外接球的表面积9．圆台的轴截面面积是Q,母线与下底面成60°角,则圆台的内切球的表面积是〔〕.〔A 〕2Q 〔B 〕23Q 〔C 〕2πQ 〔D 〕23πQ [答案]D10．已知球是棱长为的正方体的内切球,则平面截球的截面面积为.[答案]6π 11．如图,多面体ABCD EFG 的底面ABCD 为正方形,FC ＝GD ＝2EA ,其俯视图如下,则其正视图和侧视图正O 11111ABCD A B C D -1ACD O确的是<>．解析注意BE,BG在平面CDGF上的投影为实线,且由已知长度关系确定投影位置,排除A,C选项,观察B,D 选项,侧视图是指光线,从几何体的左面向右面正投影,则BG,BF的投影为虚线,故选D.答案D12．如图,在矩形ABCD中,AB＝2,BC＝3,沿BD将矩形ABCD折叠,连接AC,所得三棱锥ABCD正视图和俯视图如图,则三棱锥ABCD侧视图的面积为<>．A.错误!B.错误!C.错误!D.错误!解析由正视图与俯视图可得,在三棱锥ABCD中,平面ABD⊥平面BCD,该几何体的侧视图是腰长为错误!＝错误!的等腰直角三角形,其面积为错误!×错误!错误!＝错误!.答案B13．某几何体的三视图如图所示,则该几何体的体积为<>．A.错误!B.错误!C．200 D．240解析由三视图还原的几何体为两底面为等腰梯形的直棱柱,梯形的面积为错误!<2＋8>×4＝20,所以棱柱的体积为20×10＝200.答案C14．某四棱台的三视图如图所示,则该四棱台的体积是<>．A．4 B.错误!C.错误!D．6解析由四棱台的三视图可知该四棱台的上底面是边长为1的正方形,下底面是边长为2的正方形,高为2.由棱台的体积公式可知该四棱台的体积V＝错误!<12＋错误!＋22>×2＝错误!,故选B.。

立体几何中的与球有关的内切外接问题分解课件

公式
设多边形的边数为$n$，则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$，其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时，圆柱体的底面圆周和顶面圆周都与球面相切，且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$，顶面圆心为$O_2$，球心为$O$。由于球内切于圆柱体，所以$OO_1 = OO_2 = r$，其中$r$为球的半径。同时，圆柱体的底面圆周和顶面圆周都与球面相切，所以底面圆心到球心的距离等于底面圆的半径，顶面圆心到球心的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$，顶面半径为$R_2$，高为$h$，则球的半径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时，圆锥体的底面圆周和侧面都与球面相切，且圆锥的轴线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$，球心为$O$。由于球内切于圆锥体，所以$OO_1 = r$，其中$r$为球的半径。同时，圆锥体的底面圆周和侧面都与球面相切，所以底面圆心到球心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中，经常涉及到球与多面体的内切和外接问题，需要利用球心到多面体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用，通过这些定理可以推导出球与其他几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切

专题讲解立体几何中的外接球与内切球问题（学生版）

专题讲解立体几何中的外接球与内切球问题如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球．有关多面体外接球的问题，是立体几何的一个重点与难点，也是高考考查的一个热点。

考查学生的空间想象能力以及化归能力。

研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，解决这类问题的关键是抓住内接的特点，即球心到多面体的顶点的距离等于球的半径．并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用。

球的内切问题主要是指球外切多面体与旋转体，解答时首先要找准切点，通过作截面来解决．如果外切的是多面体，则作截面时主要抓住多面体过球心的对角面来作。

当球与多面体的各个面相切时，注意球心到各面的距离相等即球的半径，求球的半径时，可用球心与多面体的各顶点连接，球的半径为分成的小棱锥的高，用体积法来求球的半径。

球与多面体的关系是高考考查的重点，但同学们又因为缺乏较强的空间想象能力，较难找到解题的切入点和突破口。

解决这类题目是要认真分析图形，明确切点和接点的位置及球心的位置是关键。

常见题型有求对应外接球或内切球半径、表面积、体积或球内接几何体最值等问题。

本章节将对常见的关于内切球和外接球的模型作一总结，并附有针对性训练题，供教师和学生参考使用。

一.常见模型归纳1. 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型，用构造法(构造长方体)解决。

外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝a 2＋b2＋c2。

)，秒杀公式：R2＝a2＋b2＋c24．可求出球的半径从而解决问题．有以下四种类型：【例1】已知二面角α－l－β的大小为π3，点P∈α，点P在β内的正投影为点A，过点A作AB⊥l，垂足为点B，点C∈l，BC＝22，P A＝23，点D∈β，且四边形ABCD满足∠BCD＋∠DAB＝π．若四面体P ACD的四个顶点都在同一球面上，则该球的体积为________．A BCDA1B1C1D1类型ⅠA BCDA1B1C1D1类型ⅡA BCDA1B1C1D1类型ⅢA BCDA1B1C1D1例外型【例2】已知三棱锥P －ABC 的四个顶点在球O 的球面上，P A ＝PB ＝PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为( )．A ．68πB ．64πC ．62πD ．6π【变式练习1】在空间直角坐标系Oxyz 中，四面体ABCD 各顶点的坐标分别为A (2，2，1)，B (2，2，－1)，C (0，2， 1)，D (0，0，1)，则该四面体外接球的表面积是( )A ．16πB ．12πC ．43πD ．6π【变式练习2】在长方体ABCD －A 1B 1C 1D 1中，底面ABCD 是边长为32的正方形，AA 1＝3，E 是线段A 1B 1上一点，若二面角A －BD －E 的正切值为3，则三棱锥A －A 1D 1E 外接球的表面积为________．2. 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造法(构造长方体)解决。

难点突破立体图形的外接球与内切球问题

2019届高三数学第一轮复习教学案18：难点突破：立体图形的外接球与内切球问题一、基础知识与概念：1．球的截面：用一个平面去截球，截面是圆面；用一个平面去截球面，截面是圆．大圆：截面过球心，半径等于球半径（截面圆中最大）；小圆：截面不过球心． 2．球心和截面圆心的连线垂直于截面．3．球心到截面的距离d 与球半径R 及截面圆半径r 的关系：222R d r =+．4．几何体的外接球：几何体的顶点都在球面上；几何体的内切球：球与几何体的各个面都相切．球包正方体球包长方体球包四棱柱球包三棱柱三棱锥四棱锥例：1．（2017年全国卷III 第8题）已知圆柱的高为，它的两个底面的圆周在直径为的同一个球的球面上，则该圆柱的体积为A ．B ．C ．D ．π34π2π4π【解析】模式辨识：“球包体”中的“垂底侧边棱（母线）”类型，1h =，1R =，底面半径为r ，则由R =得：222213124r r ⎛⎫=+⇒= ⎪⎝⎭，234V r h ππ==．2．（2010年全国新课标卷第10题）设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为A ．B ．C ．D ．【解析】“球包体”中的“垂底侧边棱”类型，h a =，r =，222222724312h a a a R r ⎛⎫=+=+= ⎪⎝⎭，所以该球的表面积2227744123a a S R ππ==⨯=．答案B ． 3．（2014年全国大纲卷第8题）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为A ．B ．C ．D ．【解析】模式辨识：“球包体”中的“顶点连心锥”，4h =，2r ==221629284h r R h ++===，所以2818144164S R πππ==⨯=，答案：A ． 4．（2013年全国卷I 第6题）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为A ．35003cm πB ．38663cm πC ．313723cm πD ．320483cm π【解析】设水面与球的接触点（切点）为P ，球心为O ，则PO 垂直于正方体的上表面，依题意P 到正方体上表面的距离为2h =，球与正方体上表面相交圆的半径4r =，有：()2222R r R -+=，2454r R +⇒==，所以球的体积3450033V R ππ==．三、定心大法：球心在过截面圆的圆心且垂直于截面圆所在平面的直线上．两圆定心法：如下图，过两个截面圆的圆心分别作相应截面圆的垂线，由两垂线的交点确定圆心．例2：1．已知边长为ABCD 中，60∠=︒，现沿对角线BD 折起，使得二面角A BD C --为120︒，此时点A ，B ，C ，D 在同一个球面上，则该球的表面积为（） A ．20π B ．24π C ．28πD ．32πa 2a π273a π2113a π25a π814π16π9π274π2．在矩形ABCD 中，4AB =，3BC =，沿AC 将矩形折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为___________．3．在边长为1的菱形ABCD 中，60BAD ∠=︒，沿对角线将菱形折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为_____________．四、正多面体的内切球（体中球）例3：1．一个球的外切正方体的全面积为，则球的体积为_________．2．某圆锥的截面为边长为2的正三角形，则该圆锥的内切球的表面积为_______．3．（2016年全国卷III 第10题）在封闭的直三棱柱内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是A ．B ．C ．D ．【解析】考查直三棱柱中截面的内切圆为球的大圆的情景，有()13681068222AA R R ++=⨯⇒=>=，故当球半径为32时球的体积最大为344273382V R πππ9==⨯=．答案B ．练习：1．（2015年全国卷II 第9题）已知，是球的球面上两点，，为该球面上的动点，若三棱锥体积的最大值为36，则球的表面积为 A ． B ． C ． D ．2．（2016年福建漳州市5月质检）三棱锥S ABC -中，SB ⊥平面ABC ，SB =ABC ∆形，则三棱锥S ABC -的外接球的表面积为（） A ．3π B ．5π C ．9π D ．12π 3．（2014年湖南卷）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（） A ．1 B ．2 C ．3 D ．4 4．（2013年辽宁卷理10）已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上，若3AB =，111ABC A B C -4π92π6π323πA B O 90AOB ∠=︒C O ABC -O 36π64π144π256π4AC =，AB AC ⊥，112AA =，则球O 的半径为（）A．2B．C ．132D．5．（2012年全国新课标卷第11题）已知三棱锥的所有顶点都在球的球面上，是边长为的正三角形，为球的直径，且，则此棱锥的体积为A ．BC．D．6．在正三棱锥P ABC -中，PA PB PC ===，侧棱PA 与底面ABC 所成的角为60︒，则该三棱锥外接球的体积为（）A ．πB ．3πC ．4πD ．43π 7．已知底面边长为1的正四棱柱的各顶点均在同一个球面上，则该球的体积为（）A ．323πB ．4πC ．2πD ．43π 8．（2017年福建省质检）．空间四边形ABCD 的四个顶点都在同一球面上，E 、F 分别是AB 、CD 的中点，且,EF AB EF CD ⊥⊥，若8,4AB CD EF ===，则该球的半径等于A B CD 9．若三棱锥P ABC -的最长的棱2PA =，且各面均为直角三角形，则此三棱锥的外接球的体积是__________． 10．（2008年高考浙江卷理14）已知球O 的面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB BC ⊥，DA AB BC ===，则球O 的体积为____________．11．（2016年东北三省三校联考）三棱柱111ABC A B C -各顶点都在一个球面上，侧棱与底面垂直，120ACB ∠=︒，CA CB ==14AA =，则这个球的表面积为____________．12．在三棱柱111ABC A B C -中，侧棱1AA 垂直底面，90ACB ∠=︒，30BAC ∠=︒，1BC =，且三棱柱111ABC A B C -的体积为3，则三棱柱111ABC A B C -的外接球表面积为_________．13．在正三棱锥S ABC -中，M ，N 分别是棱SC 、BC 的中点，且AM MN ⊥，若侧棱SA =，则正三棱锥S ABC -外接球的表面积是____________．14．在三棱锥A BCD -中，2AB CD ==，AD BC ==AC BD ==，则三棱锥A BCD -外接球的表面积为__________． 15．（2017年天津卷）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为______．16．（2017年江苏卷）如图，在圆柱12O O 内有一个球，该球与圆柱的上、下底面及母线均相切，记S ABC -O ABC ∆1SC O 2SC =632圆柱12O O 的体积为1V ，球O 的体积为2V ，则12V V 的值是_____________．。