空间图形基本关系的认识
合集下载
1.4.1-2《空间图形基本关系的认识与空间图形的公理(1、2、3)》课件(北师大版必修2)
3.平面α ∩平面β =l,点A∈α ,B∈α ,C∈β ,且Cl,AB∩l=R,
过A、B、C三点确定平面γ ,则β ∩γ =(
(A)直线AC (C)直线CR (B)直线BC (D)以上∈AB,R∈l,又α∩β=l, ∴lβ,∴R∈β,R∈γ. 又C∈β,C∈γ,∴β∩γ=CR.
示平面， l表示直线，A、B、C表示点）
（1）若A∈l,A∈α ,B∈l,B∈α ，则l α ; （2）A∈α ,A∈β ,B∈α ,B∈β ,则α ∩β =AB； （3）若l α ,A∈l,则Aα ; （4）若A、B、C∈α ,A、B、C∈β ,且A、B、C不共线，则α
与β 重合.
则上述说法中正确的个数是__________.
将它还原为正方体，那么AB、CD、EF、GH这
四条线段所在直线是异面直线的有哪几对？ 【解析】还原为正方体如图所示，可判断AB 与CD异面，AB与GH异面，EF与GH异面.
4.（2010·湛江高一检测）正方体ABCD-A1B1C1D1中，P、Q分别
是棱AA1与CC1的中点,则经过P、B、Q三点的截面是(
(A)邻边不相等的平行四边形 (B)菱形但不是正方形 (C)矩形 (D)正方形
)
【解题提示】画截面的关键在于画面与面的交线，交线只 要有两个公共点就能画出.画出截面后可计算边长判断其形状.
一、选择题（每题4分，共16分） 1.（2010·深圳高一检测）下列说法正确的是( (A)三点确定一个面 (B)四边形一定是平面图形 )
(C)梯形一定是平面图形
(D)两个平面有不在同一条直线上的三个交点 【解析】选C.由公理2知A错，B错.
3
8.如图所示，在正方体
ABCD—A1B1C1D1中，E、F分别是
4.1空间图形基本关系的认识
c
b
B
记作： P
β
3. 空间两条直线的位置关系有三种：A
①平行直线—— 在同一个平面内，没有公 共点的两条直线。 ②相交直线—— 在同一个平面内，有且只有 一个公共点的两条直线。
α α
a
c
b
B
b 记作：a//b
a
β
a O b
记作： b O a
③异面直线— 不在任何一个平面内，没有公共点的两条直线。 —
b
α
b
a
a β b
α
γ
a
A （1）直线在平面内— 直线与平面有无数个 — 公共点。 （2）直线与平面相交— 直线与平面只 α 有一个公共点。 —
4. 空间直线与平面的位置关系有三种：
b
a
β
F
E
（3）直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种：
（1）平行平面—— 没有公共点的两个平面。 （2）相交平面—— 两个平面不重合， 并且有公共点。 α
E
β
F
练习
1.思考题：
（1）没有公共点的两条直线叫做平行直线，对吗？ （2）空间两条没有公共点的直线叫做异面直线，对吗？
（3）分别在两个平面内的两条直线一定是异面直线吗？
（4）平面内一直线与这个平面外的一条直线一定是异面直线吗？
2.说出正方体中各对线段、线段与平面的位置关系： （1）AB和CC1； D1 （2）A1 C和BD1 ； B1 A1 （3）A1 A和CB1； （4）AC和A1 C1； （5）BC与平面A1 C1； （6）B1 C与平面AC； D （7）AB与平面AC。 A B
§4
实例分析
空间几何中的垂直关系
空间几何中的垂直关系空间几何是数学中的一个重要分支，研究了在三维空间中的图形、形态和位置关系。
其中垂直关系是几何中的基本概念之一，它在建筑、工程、设计等领域都有广泛的应用。
本文将介绍空间几何中的垂直关系及其相关概念和性质。
1. 垂直关系的定义在空间几何中，两条直线、两个平面或者两个曲面相互垂直，意味着它们的方向互相垂直，不在同一平面上，并且它们的夹角是90度。
具体来说，垂直关系可以分为以下几种情况：1.1 直线的垂直关系空间中的两条直线相互垂直的判定条件有多种，最常用的方法是利用两条直线的方向向量之间的垂直性。
设直线L1的方向向量为a，直线L2的方向向量为b，若a·b=0，则直线L1与直线L2垂直。
1.2 平面的垂直关系两个平面相互垂直的判定方法一般都涉及到它们的法向量。
设平面P1的法向量为n1，平面P2的法向量为n2，若n1·n2=0，则平面P1与平面P2垂直。
1.3 直线与平面的垂直关系直线与平面相互垂直的条件也涉及到它们的方向向量和法向量。
设直线L的方向向量为a，平面P的法向量为n，若a·n=0，则直线L与平面P垂直。
2. 垂直关系的性质垂直关系有一些重要的性质，下面将介绍几个常见的性质。
2.1 垂直平面的夹角如果两个平面相互垂直，则它们的夹角是90度。
这一性质在空间几何中非常重要，可以用来判断两个平面是否相互垂直。
2.2 垂直直线与平面的关系如果一条直线垂直于一个平面，那么它一定位于该平面上的某条直径上。
这一性质可以应用到建筑设计、物理力学等领域。
2.3 垂直向量与平面的关系设一个向量与平面上的任意一条向量都垂直，那么这个向量一定垂直于该平面。
这一性质常用于计算向量与平面的垂直关系。
3. 应用实例垂直关系在实际应用中有很多场景，下面举几个例子进行说明。
3.1 平面墙与地板的垂直关系在建筑设计中，我们常常需要确保墙面与地板垂直，以保证建筑的稳定性和美观性。
3.2 直线与曲面的垂直关系在机械制造中，我们需要确保某些直线与曲面垂直，来实现零件的配合与连接。
空间点线面的位置关系(优质课)
α
a
b 记作：a//b
β
a Ob
记作：abO
③异面直线——不在任何一个平面内，没有公共点的两条直线。
b
a γ
可编辑ppt
7
小结 点、线、面之间的位置关系及语言表达
文字语言表达 图形语言表达 符号语言表达
点A在直线a上 点A不在直线a上
A
a
A
a
A∈a A∈a
点A在平面α上 点A不在平面α上 直线a在平面α内
那么这两条直线互相平行.在空间这一规律是否还成立呢?
D'
C'
观察：在右图的长方体中，
BB'// AA',DD'// AA'，那么 A '
B'
BB'与DD'平行吗？
D
C
A
B
观察 : 将一张纸如图进行折叠 , 则各折痕及边 a, b, c, d, e, …
之间有何关系？
abcde
a∥b ∥c ∥d ∥e ∥ …
空间中的点、直线、平面之间有什么位置关系，是我们接下来要讨论的问题.
D1
C1
A1
B1
D C
A
B
可编辑ppt
2
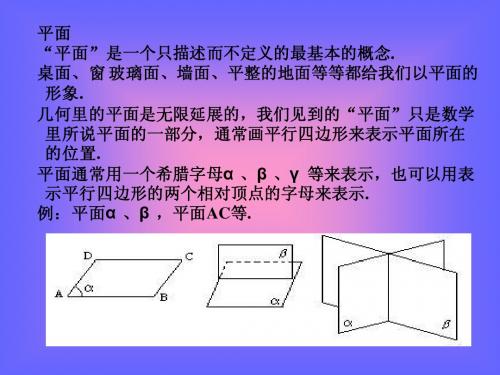
平面的概念与画法
几何里的平面是无限延展的.
常常把水平的平面画成锐角为450， 横边长等于其邻边长2倍的平行四边形.
表示①平面α、平面β、平面γ；
②用表示平行四边形的四个顶点
或两个相对顶点的字母来表示，
(1)平面α与平面β相交,它们只有有限个公共点. ×
(2)经过一条直线和这条直线外的一点,有且只有一个
平面. √
(3)经过两条相交直线,有且只有一个平面. √
空间图形的认识与绘制
特点：没有厚度，只有长度和宽度
立体图形
特点：具有明显的三维特性，可以通过组合、旋转等方式形成各种复杂的空间结构
定义：三维空间中占有一定空间的图形，具有长、宽、高三个维度
分类：长方体、正方体、圆柱体、圆锥体、球体等
应用：在建筑、机械、航天等领域中广泛应用
组合体
添加标题
添加标题
添加标题
添加标题
分类：根据组合方式的不同，可以分为叠加型、挖切型和综合型等。
大小：空间图形的大小可以通过其尺寸来衡量，如半径、直径、边长等
方向：空间图形中的方向可以通过旋转或翻转来改变
位置：空间图形中的位置可以通过坐标系来确定，如三维空间中的x、y、z轴
空间图形的位置关系
平行：空间图形中的线段或平面在无限延伸后不相交
垂直：空间图形中的线段或平面在无限延伸后相交于一点
相交：空间图形中的线段或平面在有限长度内相交
性质：具有位置，没有方向和长度
直线
定义：直线是两点之间所有点的集合
性质：无限延伸，不可度量
表示方法：用直尺或直线命令绘制
在空间图形中的应用：构成平面、形成角度和交点
平面
定义：平面是空间中无限延展、没有厚度的几何元素
表示方法：通常用平行四边形表示平面，并加上方向箭头
空间图形的基本元素：点、直线和平面
05
空间图形的应用
建筑设计中的应用
添加标题
添加标题
添加标题
添加标题
通过运用空间图形，建筑师可以更好地实现建筑设计的功能需求，提高建筑的使用舒适度和空间效率。
空间图形在建筑设计中的应用，可以创造出独特的视觉效果，增强建筑的艺术性和表现力。
空间图形可以帮助建筑师解决建筑设计中的复杂问题，如结构、采光、通风等，提高建筑的技术性和可行性。
立体图形
特点：具有明显的三维特性，可以通过组合、旋转等方式形成各种复杂的空间结构
定义：三维空间中占有一定空间的图形，具有长、宽、高三个维度
分类：长方体、正方体、圆柱体、圆锥体、球体等
应用：在建筑、机械、航天等领域中广泛应用
组合体
添加标题
添加标题
添加标题
添加标题
分类：根据组合方式的不同，可以分为叠加型、挖切型和综合型等。
大小：空间图形的大小可以通过其尺寸来衡量，如半径、直径、边长等
方向：空间图形中的方向可以通过旋转或翻转来改变
位置：空间图形中的位置可以通过坐标系来确定，如三维空间中的x、y、z轴
空间图形的位置关系
平行：空间图形中的线段或平面在无限延伸后不相交
垂直：空间图形中的线段或平面在无限延伸后相交于一点
相交：空间图形中的线段或平面在有限长度内相交
性质：具有位置，没有方向和长度
直线
定义：直线是两点之间所有点的集合
性质：无限延伸，不可度量
表示方法：用直尺或直线命令绘制
在空间图形中的应用：构成平面、形成角度和交点
平面
定义：平面是空间中无限延展、没有厚度的几何元素
表示方法：通常用平行四边形表示平面，并加上方向箭头
空间图形的基本元素：点、直线和平面
05
空间图形的应用
建筑设计中的应用
添加标题
添加标题
添加标题
添加标题
通过运用空间图形，建筑师可以更好地实现建筑设计的功能需求，提高建筑的使用舒适度和空间效率。
空间图形在建筑设计中的应用，可以创造出独特的视觉效果，增强建筑的艺术性和表现力。
空间图形可以帮助建筑师解决建筑设计中的复杂问题，如结构、采光、通风等，提高建筑的技术性和可行性。
【数学】1.4.1 空间图形基本关系的认识 课件 (北师大版必修2)
第一章 立体几何初步
4.1 空间图形基本关系的认识
构成空间图形的基本元素
• 点是构成空间图形的最基本的元素
• 线可看作是具有某一特点的点的集合， 也是构成空间图形的元素 • 面也可视为无数点的集合，同时也是构 成空间图形的元素 • 它们之间有什么关系呢？
阅读课本实验分析
• • • • • 试思考以下问题 1、点和直线有什么关系？ 2、点和平面有什么关系？ 3、直线与直线有哪些关系？ 4、平面与平面有什么关系？
异面直线：不在任何一个平面内的两条直线， 作图时为了表示异面直线不共面的特点通 常用一个或两个平面来衬托
例 如图是一个正方体的展开图，如果将它还 原为正方体，那么AB、CD、EF、GH这四条 线段所在的直线是异面直线的有 __________对，分别是______________？
解：3对，分别是AB、GH；AB、CD；GH、EF。
空间直线与平面的位置关 系
空间平面与平面的位置关 系
• 空间平面与平面的位置关系：平行；相 交
ห้องสมุดไป่ตู้
空间点与线的关系
• 空间点与直线的位置关系有两种：
点 P 在直线 上：
点 P 在直线 外： ；
空间点与平面的关系
• 空间点与平面的位置关系有两种：
空间直线与直线的位置关 系
平行直线：在同一平面内但没有公共点的两条直线， 记作：a∥b 相交直线：在同一平面内有且只有一个公共点的两 条直线，记作a∩b=P
4.1 空间图形基本关系的认识
构成空间图形的基本元素
• 点是构成空间图形的最基本的元素
• 线可看作是具有某一特点的点的集合， 也是构成空间图形的元素 • 面也可视为无数点的集合，同时也是构 成空间图形的元素 • 它们之间有什么关系呢？
阅读课本实验分析
• • • • • 试思考以下问题 1、点和直线有什么关系？ 2、点和平面有什么关系？ 3、直线与直线有哪些关系？ 4、平面与平面有什么关系？
异面直线：不在任何一个平面内的两条直线， 作图时为了表示异面直线不共面的特点通 常用一个或两个平面来衬托
例 如图是一个正方体的展开图，如果将它还 原为正方体，那么AB、CD、EF、GH这四条 线段所在的直线是异面直线的有 __________对，分别是______________？
解：3对，分别是AB、GH；AB、CD；GH、EF。
空间直线与平面的位置关 系
空间平面与平面的位置关 系
• 空间平面与平面的位置关系：平行；相 交
ห้องสมุดไป่ตู้
空间点与线的关系
• 空间点与直线的位置关系有两种：
点 P 在直线 上：
点 P 在直线 外： ；
空间点与平面的关系
• 空间点与平面的位置关系有两种：
空间直线与直线的位置关 系
平行直线：在同一平面内但没有公共点的两条直线， 记作：a∥b 相交直线：在同一平面内有且只有一个公共点的两 条直线，记作a∩b=P
高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理
第十二页，共42页。
[小组合作型]
空间点、线、面的位置(wèi zhi)关系
(1)如果 a α，b α，l∩a＝A，l∩b＝B，l β，那么 α 与 β 的位置关系是________．
(2)如图 1-4-1，在正方体 ABCD-A′B′C′D′中， 哪几条棱所在的直线与直线 BC′是异面直线？
图 1-4-1
第十页，共42页。
两个平面若有三个公共点，则这两个平面( )
A．相交
B．重合
C．相交或重合
D．以上都不对
【解析】 若三个点在同一条直线上，则两平面可能相交；若这三个点不 在同一直线上，则这两个平面重合．
【答案】 C
第十一页，共42页。
[质疑·手记] 预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问 1： _____________________________________________________ 解惑： _______________________________________________________ 疑问 2： _____________________________________________________ 解惑： _______________________________________________________ 疑问 3： ______________________________________________________ 解惑： _______________________________________________________
平面与平面 的位置关系
面面平行 面面相交
α∥β α∩β＝a
第五页，共42页。
[小组合作型]
空间点、线、面的位置(wèi zhi)关系
(1)如果 a α，b α，l∩a＝A，l∩b＝B，l β，那么 α 与 β 的位置关系是________．
(2)如图 1-4-1，在正方体 ABCD-A′B′C′D′中， 哪几条棱所在的直线与直线 BC′是异面直线？
图 1-4-1
第十页，共42页。
两个平面若有三个公共点，则这两个平面( )
A．相交
B．重合
C．相交或重合
D．以上都不对
【解析】 若三个点在同一条直线上，则两平面可能相交；若这三个点不 在同一直线上，则这两个平面重合．
【答案】 C
第十一页，共42页。
[质疑·手记] 预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问 1： _____________________________________________________ 解惑： _______________________________________________________ 疑问 2： _____________________________________________________ 解惑： _______________________________________________________ 疑问 3： ______________________________________________________ 解惑： _______________________________________________________
平面与平面 的位置关系
面面平行 面面相交
α∥β α∩β＝a
第五页，共42页。
空间图形的基本关系与公理(1)
分析 可先转换成符号语言，再作图．
解 (1)A∈α，B∈α，A∈l，B∈l
(2)l α，P∈l，P∈α.
(3)α∩β＝l，m α，m∥l.
变式训练
将下面用符号语言表示的关系改用文
字语言予以叙述，并且用图形语言予以表示．
解 文字语言叙述为： 点 A 在平面 α 与平面 β 的交线 l 上，AB、AC 分 别在 α、β 内． 图形语言表示为如图所示．
B α
A
（2）点在平面外
记作：
B
空间两条直线的位置关系有三种：
①平行直线——
在同一个平面内，没有公共点的两条直线.
②相交直线—— 在同一个平面内，有且只有一个公共点的两
条直线.
记作：a//b a b α
b
记作： β
ab O
a O b b
③异面直线——不同在任何一个平面内
α a
a
β b
④若直线 a∥直线 b，b α，那么直线 a 平行于平面α内的
变式训练
下面命题中正确的个数是
( C )
①如果 a、b 是两条直线，a∥b，那么 a 平行于经过 b 的任何一个平面； ②如果直线 a 满足 a∥α，那么 a 与平面α内的任何 一条直线平行； ③如果直线 a、b 满足 a∥α，b∥α，则 a∥b； ④如果直线 a、 和平面α满足 a∥b， α， α， b a∥ b 那么 b∥α； ⑤如果 a 与平面α上的无数条直线平行，那么直线 a 必平行于平面α. A．0 B．2 C．1 D．3
解析
A、B 都不能保证 α、β 无公共点，如图 1
所示；C 中当 a∥α，a∥β 时 α 与 β 可能相交，如 图 2 所示；只有 D 说明 α、β 一定无公共点．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平面 “平面”是一个只描述而不定义的最基本的概念. 桌面、窗 玻璃面、墙面、平整的地面等等都给我们以平面的 形象. 几何里的平面是无限延展的，我们见到的“平面”只是数学 里所说平面的一部分，通常画平行四边形来表示平面所在 的位置. 平面通常用一个希腊字母α、β、γ等来表示，也可以用表 示平行四边形的两个相对顶点的字母来表示. 例：平面α、β，平面AC等.
（3）分别在两个平面内的两条直线一定是异面直线吗？
（4）平面内一直线与这个平面外的一条直线一定是异面直线吗？
2.说出正方体中各对线段、线段与平面的位置关系：
（1）AB和CC1； （2）A1 C和BD1 ； （3）A1 A和CB1； （4）AC和A1 C1； （5）BC与平面A1 C1； （6）B1 C与平面AC；
（7）AB与平面AC。
D1 A1
C1 B1
D
C
A B
①点在直线上
A
aA
a
记作：A a
②点在直线外 b
记作：B b
B
α
c
b
B
2.空间点与平面的位置关系有两种：
P
①点在平面内 记作：O
②点在平面外
记作： P
O β
3.
空间两条直线的位置关系有三种：
A
①平行直线—— 在同一个平面内，没有公
共点的两条直线。
②相交直线—— 在同一个平面内，有且只有 α
一个公共点的两条直线。
α
aБайду номын сангаас
b 记作：a//b
β
a Ob
a
c
b
B
记作：a b O
③异面直线— —
b
a α
不在任何一个平面内，没有公共点的两条直线。
α
b
a
β
b
a
γ
4. 空间直线与平面的位置关系有三种：
A
b
a
（1）直线在平面内— 直线与平面有无数个
—
公共点。
（2）直线与平面相交— —
直线与平面只 有一个公共点。
空间图形是丰富的，它由一些基本的点、线、面所组 成。研究清楚它们的位置关系，对于我们认识空间图 形是很重要的。
§4 空间图形的基本关系与公理
4.1 空间图形基本关系的认识
实例分析
观察下列长方体，回答问题。
A
a
α
c
b
B
问题
(1)长方体有几个顶点？
（2）长方体有几条棱？
（3）长方体有几个表面？
1.空间点与直线的位置关系有两种：
α
β
E
F
（3）直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种：
（1）平行平面—— 没有公共点的两个平面。
（2）相交平面—— 两个平面不重合，
α
β
并且有公共点。
E
F
练习
1.思考：
（1）没有公共点的两条直线叫做平行直线,对吗
（2）空间两条没有公共点的直线叫做异面直线,对吗
（3）分别在两个平面内的两条直线一定是异面直线吗？
（4）平面内一直线与这个平面外的一条直线一定是异面直线吗？
2.说出正方体中各对线段、线段与平面的位置关系：
（1）AB和CC1； （2）A1 C和BD1 ； （3）A1 A和CB1； （4）AC和A1 C1； （5）BC与平面A1 C1； （6）B1 C与平面AC；
（7）AB与平面AC。
D1 A1
C1 B1
D
C
A B
①点在直线上
A
aA
a
记作：A a
②点在直线外 b
记作：B b
B
α
c
b
B
2.空间点与平面的位置关系有两种：
P
①点在平面内 记作：O
②点在平面外
记作： P
O β
3.
空间两条直线的位置关系有三种：
A
①平行直线—— 在同一个平面内，没有公
共点的两条直线。
②相交直线—— 在同一个平面内，有且只有 α
一个公共点的两条直线。
α
aБайду номын сангаас
b 记作：a//b
β
a Ob
a
c
b
B
记作：a b O
③异面直线— —
b
a α
不在任何一个平面内，没有公共点的两条直线。
α
b
a
β
b
a
γ
4. 空间直线与平面的位置关系有三种：
A
b
a
（1）直线在平面内— 直线与平面有无数个
—
公共点。
（2）直线与平面相交— —
直线与平面只 有一个公共点。
空间图形是丰富的，它由一些基本的点、线、面所组 成。研究清楚它们的位置关系，对于我们认识空间图 形是很重要的。
§4 空间图形的基本关系与公理
4.1 空间图形基本关系的认识
实例分析
观察下列长方体，回答问题。
A
a
α
c
b
B
问题
(1)长方体有几个顶点？
（2）长方体有几条棱？
（3）长方体有几个表面？
1.空间点与直线的位置关系有两种：
α
β
E
F
（3）直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种：
（1）平行平面—— 没有公共点的两个平面。
（2）相交平面—— 两个平面不重合，
α
β
并且有公共点。
E
F
练习
1.思考：
（1）没有公共点的两条直线叫做平行直线,对吗
（2）空间两条没有公共点的直线叫做异面直线,对吗