3.电测法测定材料弹性模量和泊松比实验报告
材料弹性常数Eμ的测定——电测法测定弹性模量E和泊松比μ

材料弹性常数Eμ的测定——电测法测定弹性模量E和泊松比μ材料的弹性常数是描述材料在受力作用下的变形性能的指标,常用的弹性常数有弹性模量E和泊松比μ。
弹性模量E是材料受力后单位应力引起的单位变形量,而泊松比μ是指材料沿一个方向的单位变形引起的另一个方向单位变形的比值。
在实际工程中,需要准确测定材料的弹性常数,以便设计和计算工程结构的变形和应力分布。
其中,弹性模量E的测定是相对简单和常用的,主要有拉伸试验、压缩试验和弯曲试验等方法。
而泊松比μ则需要通过更复杂的测试方法进行测定。
本文主要介绍电测法测定材料的弹性模量E和泊松比μ的原理和应用。
一、电测法测定弹性模量E电测法是通过测量材料受力后的电阻变化来间接计算材料的弹性模量。
根据导体的电阻与其长度、横截面积和电阻率之间的关系,当材料受到力作用后,其长度和横截面积都会发生变化,从而导致电阻发生变化。
由此可以利用电阻与长度和横截面积的关系,计算出材料的弹性模量。
电测法测定弹性模量E的步骤如下:1.制备测量样品:首先制备出符合测量要求的样品,通常为长条形状,并且长度和横截面积要容易测量。
2.安装测量装置:将样品安装在测量装置上,一般采用四点法或截面法进行测量。
在四点法中,两对电极分别用来传输电流和测量电压。
在截面法中,材料上有两组电极,用来传输电流和测量电压。
3.施加载荷:施加拉力或压力载荷到样品上,使其发生变形。
4.记录电阻变化:通过测量电阻的变化,可以得到材料受力后的长度变化。
5.计算弹性模量E:利用导线的电阻与线长、横截面积和电阻率的关系,结合样品的长度变化,可以计算出材料的弹性模量。
电测法测定弹性模量E的优点是测量简便、快速,对试样的要求相对较低,可以测量各种类型的材料。
但是该方法的准确性受到试样的尺寸和形状的限制,并且测量结果受到试样固定约束的影响。
二、电测法测定泊松比μ泊松比μ描述了材料在沿一个方向的拉伸或压缩应力下,垂直于该方向的单位变形的比值。
材料弹性常数E、μ测定——电测法测定弹性模量E及泊松比μ

实验名称:材料弹性常数 E、μ的测定班级: 姓名: 学号: 同组者:一、实验目的测量金属材料的弹性模量E和泊松比μ;验证单向受力胡克定律;学习电测法的根本原理和电阻应变仪的根本操作。
二、实验仪器和设备1.微机控制电子万能试验机;2.电阻应变仪;3.游标卡尺。
三、试件中碳钢矩形截面试件,名义尺寸为bt=(166)mm;2材料的屈服极限s 360MPa。
四、实验原理和方法1、实验原理:材料在比例极限内服从虎克定律,在单向受力状态下,应力与应变成正比:E〔1〕上式中的比例系数E称为材料的弹性模量。
由以上关系,可以得到:P〔2〕EA材料在比例极限内,横向应变与纵向应变之比的绝对值为一常数:〔3〕上式中的常数称为材料的横向变形系数或泊松比。
本实验采用增量法,即逐级加载,分别测量在各相同载荷增量P作用下,产生的应变增量i 于是式〔2〕和式〔3〕分别写为:P〔4〕EiA0ii〔5〕ii根据每级载荷得到的 E i和i,求平均值:n EiE i1〔6〕nnii1〔7〕n以上即为实验所得材料的弹性模量和泊松比。
上式中n为加载级数。
2、实验方法〔1〕、电测法电测法根本原理:电测法是以电阻应变片为传感器, 通过测量应变片电阻的改变量来确定构件应变,并进一步利用胡克定律或广义胡克定律确定相应的应力的实验方法。
试验时,将应变片粘贴在构件外表需测应变的部位, 并使应变片的纵向沿需测应变的方向。
当构件该处沿应变片纵向发生正应变时,应变片也产生同样的变形。
这时,敏感栅的电阻由初始值R变为R+ R。
在一定范围内,敏感栅的电阻变化率R/R与正应变ε成正比,即:RR k上式中,比例常数k为应变片的灵敏系数。
故只要测出敏感栅的电阻变化率,即可确定相应的应变。
电阻应变仪测点桥的原理:电桥B、D端的输出电压为:UBDR1R4R2R3UR2)(R3R4)(R1当每一电阻分别改变R1, R2, R3,R4时,B、D端的输出电压变为:U(R1R1)(R4R4)(R2R2)(R3R3 )U(R1R1R2R2)(R3R3R4R4)略去高阶小量,上式可写为:U BD U R1R2 2(R1R2R3R4) (R1R2)R1R2R3R4在测试时,一般四个电阻的初始值相等,那么上式变为:UBD U(R1R2R3R4) 4R1R2R3R4得到:kUUBD(1234)4电阻应变仪的根本测量电路如果将应变仪的读数按应变标定,那么应变仪的读数为:4U BD(1234)kU〔2〕、加载方法——增量法与重复加载法增量法可以验证力与变形之间的线性关系,假设各级载荷增量P 相同,相应的应变增量也应大致相等,这就验证了虎克定律,如右图所示。
弹性参数测定实验报告(3篇)

第1篇一、实验目的1. 熟悉弹性参数测定的基本原理和方法;2. 掌握测定材料的弹性模量、泊松比等弹性参数的实验步骤;3. 培养实验操作技能和数据分析能力。
二、实验原理弹性参数是描述材料在受力后发生形变与应力之间关系的物理量。
本实验采用拉伸试验方法测定材料的弹性模量和泊松比。
1. 弹性模量(E):在弹性范围内,应力(σ)与应变成正比,比值称为材料的弹性模量。
其计算公式为:E = σ / ε其中,σ为应力,ε为应变成分。
2. 泊松比(μ):在弹性范围内,横向应变(εt)与纵向应变(εl)之比称为泊松比。
其计算公式为:μ = εt / εl三、实验仪器与材料1. 仪器:材料试验机、游标卡尺、引伸计、应变仪、万能试验机、数据采集器等;2. 材料:低碳钢拉伸试件、标准试样、引伸计、应变仪等。
四、实验步骤1. 准备工作:将试样安装到材料试验机上,调整好试验机夹具,检查实验设备是否正常;2. 预拉伸:对试样进行预拉伸,以消除试样在安装过程中产生的残余应力;3. 拉伸试验:按照规定的拉伸速率对试样进行拉伸,记录拉伸过程中的应力、应变等数据;4. 数据处理:根据实验数据,计算弹性模量和泊松比;5. 结果分析:对比实验结果与理论值,分析误差产生的原因。
五、实验结果与分析1. 弹性模量(E)的计算结果:E1 = 2.05×105 MPaE2 = 2.00×105 MPaE3 = 2.03×105 MPa平均弹性模量E = (E1 + E2 + E3) / 3 = 2.01×105 MPa2. 泊松比(μ)的计算结果:μ1 = 0.296μ2 = 0.293μ3 = 0.295平均泊松比μ = (μ1 +μ2 + μ3) / 3 = 0.2943. 结果分析:实验结果与理论值较为接近,说明本实验方法能够有效测定材料的弹性参数。
实验过程中,由于试样安装、试验机夹具等因素的影响,导致实验结果存在一定的误差。
材料弹性常数E、μ的测定——电测法测定弹性模量E和泊松比μ
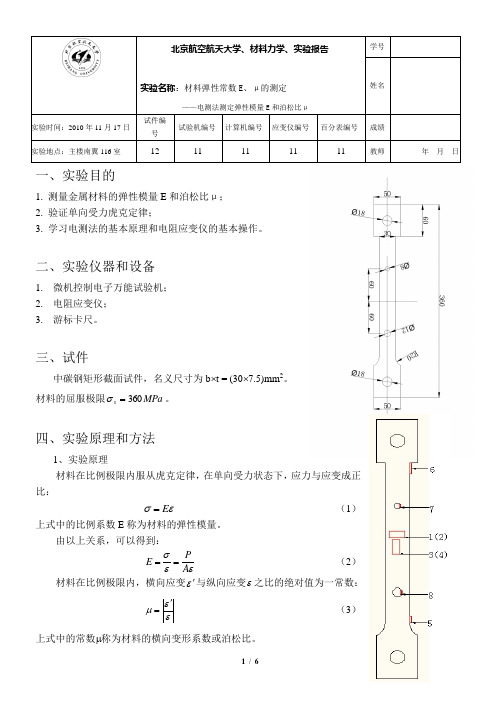
北京航空航天大学、材料力学、实验报告实验名称:材料弹性常数E 、μ的测定——电测法测定弹性模量E 和泊松比μ学号姓名实验时间:2010年11月17日 试件编号试验机编号 计算机编号 应变仪编号百分表编号成绩实验地点:主楼南翼116室12 11 11 11 11教师年 月 日一、实验目的1. 测量金属材料的弹性模量E 和泊松比μ;2. 验证单向受力虎克定律;3. 学习电测法的基本原理和电阻应变仪的基本操作。
二、实验仪器和设备1. 微机控制电子万能试验机;2. 电阻应变仪;3. 游标卡尺。
三、试件中碳钢矩形截面试件,名义尺寸为b ⨯t = (30⨯7.5)mm 2。
材料的屈服极限MPa s 360=σ。
四、实验原理和方法1、实验原理材料在比例极限内服从虎克定律,在单向受力状态下,应力与应变成正比:εσE = (1)上式中的比例系数E 称为材料的弹性模量。
由以上关系,可以得到:PE A σεε== (2)材料在比例极限内,横向应变ε'与纵向应变ε之比的绝对值为一常数:εεμ'=(3) 上式中的常数μ称为材料的横向变形系数或泊松比。
本实验采用增量法,即逐级加载,分别测量在各相同载荷增量∆P 作用下,产生的应变增量∆εi 。
于是式(2)和式(3)分别写为:ii A PE ε∆∆=0 (4) ii i εεμ∆'∆= (5)根据每级载荷得到的E i 和μi ,求平均值:n E E ni i∑==1(6)nni i∑==1μμ (7)以上即为实验所得材料的弹性模量和泊松比。
上式中n 为加载级数。
2、实验方法2.1电测法电测法基本原理:电测法是以电阻应变片为传感器,通过测量应变片电阻的改变量来确定构件应变,并进一步利用胡克定律或广义胡克定律确定相应的应力的实验方法。
试验时,将应变片粘贴在构件表面需测应变的部位,并使应变片的纵向沿需测应变的方向。
当构件该处沿应变片纵向发生正应变时,应变片也产生同样的变形。
试验一 弹性模量和泊松比的测定实验

试验一弹性模量和泊松比的测定实验弹性模量和泊松比的测定实验大纲1. 通过材料弹性模量和泊松比的测定实验,使学生掌握测定材料变形的基本方法,学会拟定实验加载方案,验证虎克定律。
2. 电测材料的弹性模量和泊松比,使学生学会用电阻应变计和电阻应变仪测量材料的变形。
主要设备:材料试验机或多功能电测实验装置;主要耗材:低碳钢拉伸弹性模量试样,每次实验1根。
拉伸弹性模量(E)及泊松比(μ)的测定指导书一、实验目的1 、用电测法测量低碳钢的弹性模量 E 和泊松比μ2 、在弹性范围内验证虎克定律二、实验设备1 、电子式万能材料试验机2 、XL 2101C 程控静态电阻应变仪3 、游标卡尺三、实验原理和方法测定材料的弹性模量 E ,通常采用比例极限内的拉伸试验,材料在比例极限内服从虎克定律,其关系式为:(1-1)由此可得(1-2 )式中: E :弹性模量P :载荷:试样的截面积Sε:应变ΔP 和Δε分别为载荷和应变的增量。
由公式(1-2)即可算出弹性模量 E 。
实验方法如图1-1所示,采用矩形截面的拉伸试件,在试件上沿轴向和垂直于轴向的两面各贴两片电阻应变计,可以用半桥或全桥方式进行实验。
1、半桥接法:把试件两面各粘贴的沿轴向(或垂直于轴向)的两片电阻应变计(简称工作片)的两端分别接在应变仪的A、B 接线端上,温度补偿片接到应变仪的B、C 接线端上,然后给试件缓慢加载,通过电阻应变仪即可测出对应载荷下的轴向应变轴r ε值(或横向应变值横r ε)。
再将实际测得的值代入(1-2)式中,即可求得弹性模量 E 之值。
2、全桥接法:把两片轴向(或两片垂直于轴向)的工作片和两片温度补偿片按图1-1中(a)( 或(b)) 的接法接入应变仪的 A 、 B 、 C 、 D 接线柱中,然后给试件缓慢加载,通过电 阻应变仪即可测出对应载荷下的轴向应变值轴r ε(或垂直于轴向横r ε),将所测得的ε值代入(1-2)式中,即可求得弹性模量 E 之值。
实验三 矩形截面悬臂梁弯曲测弹性模量和泊松比

中国矿业大学力学实验报告姓名白永刚 班级 土木11-9班 同组姓名 方雷、蔡卫、蔡尧 实验日期2012-10-26材料弹性模量E 和泊松比μ的测试一、实验目的1. 测定常用金属材料的弹性模量E 和泊松比μ。
2. 验证胡克定律。
3. 学习掌握电测法的基本原理和电阻应变仪的操作。
4. 熟悉测量电桥的应用。
掌握应变片在测量电桥中的各种接线方法。
5.学习用最小二乘法处理实验数据。
二、实验设备1. 电子万能试验机或组合实验台;2. 静态电阻应变测力仪;3. 游标卡尺;4. 矩形截面梁。
三、实验原理和方法材料在线弹性范围内服从胡克定律,应力和应变成正比关系。
单向拉伸时,其形式为E σε= (1) 式中E 为弹性模量。
在εσ-曲线上,E 由弹性阶段直线的斜率确定,它表征材料抵抗弹性应变的能力。
E 愈大,产生一定弹性变形所需的应力愈大。
E 是弹性元件选材的重要依据,是力学计算中的一个重要参量。
00F =l E A lσε=∆ (2)试件弯曲时,产生纵向伸长和横向收缩,或者产生纵向收缩和纵向伸长。
实验表明在弹性范围内,横向应变ε'与轴向应变ε,二者之比为一常数,其绝对值称为泊松比,用μ来表示,即εεμ'=(3)本实验采用电测法来测量E 、μ。
试件采用矩形截面试件,布片方式如图(a)。
在试件中央某截面,沿前后两面轴向分别对称地分布有两对轴向应变片R 1,R 1’以测量轴向应变ε。
一对横向应变片R 2,R 2’以测轴向应变ε'。
1. 测弹性模量E由于实验装置和安装初始状态的不稳定性,拉伸曲线的初始阶段往往是非线性的。
为了尽可能减少测量误差,实验已从初载()000F F ≠开始。
与0F 对应的应变仪读数d ε可预调到零。
采用增量法,分级加载,分别测量在各项同载荷增量F ∆作用下,产生的应变增量ε∆,并求ε∆的平均值。
设试件初始横截面面积为A 0,又因=/l l ε∆,则(2)式可写成0A F E ε∆=∆均(4)上式即为增量法测E 得计算公式,其中d ε∆为试件实际轴向应变增量的平均值,F∆为加载力的阶段差值。
弹性模量和泊松比的测定

枚应变计接入应变仪。温度补偿片贴在不受力与试件相同的材料
上。 实验时,对前后2枚轴向片和横向片各进行单片测量,并取 其平均值
b h
l
1 3
2
t
2 4
2
作为测量结果,这样消除了加载时试样偏心弯曲引起的测量误差。
实验项目名称:弹性模量和泊松比的测定
A R内
UBD
UAC
半桥接线示意图
k d ( 1 2) k仪
实验项目名称:弹性模量和泊松比的测定
全桥:测量桥路的四臂均接工作应变计
CH01 CH02 CH08 公共补偿
B R1 A R4
全桥
R2 C R3 D UAC UBD
A B B0 C D
A B B0 C D
A B B0 C D
d k ( 1 t ) t k 1 k仪 k仪
实验项目名称:弹性模量和泊松比的测定
双臂工作半桥:在AB、BC端接工作应变计
CH01 CH02 CH08 公共补偿
B R1 R2 C R内 D
半桥
A B B0 C D
A B B0 C D
A B B0 C D
A D W0 W W1
40
45 50
实验项目名称:弹性模量和泊松比的测定 GB/T22315-2008 金属材料弹性模量和泊松比试验方法
实验项目名称:弹性模量和泊松比的测定
实验原理
单向拉伸时材料在线弹性范围内服从胡克定律,应力和应变成正比关系。
E
比例系数E 称为材料的弹性模量。在σ-曲线上,E 是弹性阶段直线的
6位LED 显示力值
4个测力 功能按键
弹性模量E和泊松比

00EA A P==εσε弹性模量E 和泊松比µ的测定拉伸试验中得到的屈服极限бb 和强度极限бS ,反映了材料对力的作用的承受能力,而延伸率δ 或截面收缩率ψ,反映了材料缩性变行的能力,为了表示材料在弹性范围内抵抗变行的难易程度,在实际工程结构中,材料弹性模量E 的意义通常是以零件的刚度体现出来的,这是因为一旦零件按应力设计定型,在弹性变形范围内的服役过程中,是以其所受负荷而产生的变性量来判断其刚度的。
一般按引起单为应变的负荷为该零件的刚度,例如,在拉压构件中其刚度为:式中 A 0为零件的横截面积。
由上式可见,要想提高零件的刚度E A 0,亦即要减少零件的弹性变形,可选用高弹性模量的材料和适当加大承载的横截面积,刚度的重要性在于它决定了零件服役时稳定性,对细长杆件和薄壁构件尤为重要。
因此,构件的理论分析和设计计算来说,弹性模量E 是经常要用到的一个重要力学性能指标。
在弹性范围内大多数材料服从虎克定律,即变形与受力成正比。
纵向应力与纵向应变的比例常数就是材料的弹性模量E ,也叫杨氏模量。
横向应变与纵向应变之比值称为泊松比µ,也叫横向变性系数,它是反映材料横向变形的弹性常数。
因此金属才料拉伸时弹性模量E 地测定是材料力学最主要最基本的一个实验,下面用电测法测定低碳钢弹性模量E 和泊松比µ。
(一) (一) 试验目的1.1.用电测方法测定低碳钢的弹性模量E 及泊松比µ;2.2.验证虎克定律;3.3.掌握电测方法的组桥原理与应用。
(二) (二) 试验原理1.测定材料弹性模量E 一般采用比例极限内的拉伸试验,材料在比例极限内服从虎克定律,其荷载与变形关系为:0EA PL L ∆=∆ (1)若已知载荷ΔP 及试件尺寸,只要测得试件伸长ΔL 即可得出弹性模量E 。
(2)由于本试验采用电测法测量,其反映变形测试的数据为应变增量,即(3) 所以(2)成为:)(A L PL E ∆∆∆=0)(L L ∆∆=∆ε(4) 式中: ΔP ——载荷增量,kN ;A 0-----试件的横截面面积,cm为了验证力与变形的线性关心,采用增量法逐级加载,分别测量在相同载荷增量 ΔP 作用下试件所产生的应变增量Δε。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
深圳大学实验报告课程名称:
实验项目名称:电测法测定材料的弹性模量及泊松比学院:
专业:
指导教师:
报告人:姓名:学号:班级:
姓名:学号:班级:
姓名:学号:班级:
姓名:学号:班级:
姓名:学号:班级:实验时间:
实验报告提交时间:
教务处制
一、实验目的
二、实验设备
静态电阻应变仪型号:
实验装置名称型号:
量具名称精度㎜
三、实验数据及处理
板试件尺寸:试件截面宽b=㎜,高h=㎜,截面积
A=m m2
o
数据处理方法: (1)平均法:均
均
εσε∆∆=
∆∆=o A F E 均
均εεμ∆'∆=
计算过程:
(2)最小二乘法:∑∑===
n i i
n
i i
i
E 1
21)(εεσ
∑∑=='
=
n
i i
n
i i i
1
2
1)
(ε
εε
μ 计算过程:
四、画出ε
σ-关系图
平均法
最小二乘法
五、思考题
1.试件尺寸和形式对测定弹性模量E有无影响?
2.影响实验结果的因素有那些?为何要用等量增载法进行实验?
注:1、报告内的项目或内容设置,可根据实际情况加以调整和补充。
2、教师批改学生实验报告时间应在学生提交实验报告时间后10日内。
