单一参数正弦交流电路的分析计算小结剖析
合集下载
正弦交流电路的分析计算

2. 相位相同
3. 有效值关系:U IR
4. 相量关系:设 U U 0
则 I U 0 或 R
I U
U I R
(3-43)
电阻电路中的功率
1. 瞬时功率 p:瞬时电压与瞬时电流的乘积
i
u
R
i 2 I sin ( t) u 2U sin ( t)
p u i Ri 2 u 2 / R
则: I2 100 5 j5 10 2 45 A
I1 1090 j10 A I I1 I2 100 A A读数为 10安
R uR 若 i 2Isin t
u L uL 则 u 2IRsin t
C
uC
2I (L) sin(t 90 ) 2I ( 1 ) sin(t 90 )
C
(3-69)
相量模型
I
R U R
U
L U L
C U C
相量方程式:
U U R U L UC
设 I I0(参考相量)
则 U R IR
电感电路中复数形式的 欧姆定律
U I j X L
U U 领先!
其中含有幅度和相位信息
I
u、i 相位不一致 !
u iL ?
(3-51)
关于感抗的讨论
感抗(XL =ωL )是频率的函数, 表示电感电路中电
压、电流有效值之间的关系,且只对正弦波有效。
XL
+R
_e L
UL I XL
ω
ω=0时
XL = 0
P UI cos Q UI sin
S UI
S
Q
P
(有助记忆)
(3-82)
R、L、C 串联电路中的功率关系
单一参数正弦交流电路分析

? 平均功率或有功功率 P=0
iut+-p
,
? 无功功率 QC
iQ
C
用无功功率 QC衡量电容元件与外界交换能量的规模,即
无功功率计算式
QC
?
?UI
?
?I 2 XC
?
?
U2 XC
无功功率单位 乏尔(Var)
交换能量过程分析 p ? ui ? ?U Isin2? t
i
u
ωt
i
i
u
u
i
i
u
u
p 放电 P > 0 放电
教学内容 电阻R、电感 L、电容 C元件的电压电流关系,相 量形式的基尔霍夫定律( KVL、KCL)。
教学要求 1.掌握单一元件的电压电流关系。 2.熟练应用相量形式的 KVL、KCL进行电路分
析。 教学重点和难点
重点: 单一元件的电压电流关系和相量形式的 基尔霍夫定律应用。
难点: 电阻 R、电感 L、电容 C元件电压电流关 系的分析。
【讨论】 指出下列各式中哪些是对的,哪些是错的?
在电阻电路中: 在电感电路中:
在电容电路中:
I?U R
i? U R
i? u R
I? ? U? R
i? u XL
U ? jωL I
I? U ωL
U? I?
?
jX L
U? I?
?
XL u
?
L di dt
i? u ωL
U ? I ?ω C
u ? i ?X C
三、纯电容电路
1.电容元件
定义电容为 C ? q
u
根据电流 i ? dq dt
i ? C duc dt
电工学复习(知识点及练习题)

5.如图,已知Va、Vb ,则支路电路I 应为( C
)。
Va Vb IR US
A
(Va Vb) US I R
( B) I
US (Va Vb) R
C
I
(Va Vb) U S R
6.电位与参考点有关,是相对的( √ ),电压与参考点无关, 是绝对的( √ )。 7.在直流电路中,电感相当于开路,电容相当于短路( × )
13.中线上绝对禁止安装熔断器,但是可以安装开关( × )
△ Y 14.三相负载有________ 和_______ 两种连接方式,若各相负 对称负载 。 载的阻抗相等,则该三相负载称为__________
15. 对称三相电路的特点是:相电压、线电压、相电流 对称 。 和线电流都______
16.电路如图所示,电流表的读数为5A、电压表 读数为220V,功率表读数为550W。 求电路中的R 和XL 解:
E 10
6
V
19.
如图所示电路中,已知电流表A1、A2、A3的读数都是50A,
解:
求电路中电流表A的读数。
I3
I I1
U
∴电流表A的读数是50A
I2
20 如图所示电路中,已知电压表V1、V2、V3的读数都是60V, 求电路中电压表V的读数。 解:
U2
U U1
I
∴电压表V的读数是60V
(3) i 20sin(t 90)A (4) e 10 2 sin(314t )V
6
u 141.4sin(t )V 3
解: (1) I 100 300 A (2) U 141.4 100 V
《电工技术基础与仿真(Multisim 10)》项目4单相正弦交流电路分析

p
ui
Im
sin tU m
sin(t
2
)
U m I m cos t sin t
UI sin 2t
在电感元件的交流电路中,没有任何能量消耗,只 有电源与电感元件之间的能量交换,其能量交换的 规模用无功功率Q来衡量,它的大小等于瞬时功率 的幅值。
QL UI I 2 X L
4.2.3 纯电容电路
将开关K1闭合,K2和K3断开,分别按给定的频 率值调节信号源的频率,每次在信号发生器中设 置好频率后,打开仿真开关,双击万用表符号, 得到测量数据,
任务3 相量法分析正弦交流电路
4.3.1 RLC串联电路 1.RLC串联电路电压电流关系 (1)瞬时关系 由于电路是串联的,所以流过R、L、C三元
件的电流完全相同
1 Z1
1 Z2
(2)复阻抗并联的分流关系
I1
U Z1
I
Z Z1
I
Z2 Z1 Z2
U
I2
I Z1 Z1 Z2
I I1 I2 Z1 Z2
a)
I
U
Z
b)
4.3.3 功率因数的提高
1.提高功率因数的意义 功率因数愈大,所损耗的功率也就愈小,
输电效率也就愈高。 负载的功率因数 愈高,发电机可提供的有
1.电压与电流的关系 线性电容元件在图所示的关联方向的条件下
iC
C duc dt
i +
u
C
_
i C duc dt
C dUm sin t
dt
U mC cost
U
mC
s
in(t
2
)
据此,可得出电容元件电压与电流关系的结论:
3.3单一参数的正弦交流电路

Um Im sin2 ω t (2) 平均2功率 P
UI
sin 2 ω t
P 1
T
p dt
T0
1
T
UI sin (2ω t)dt 0
T0
C是非耗 能元件
瞬时功率 :p i u UI sin2ωt
u,i i u
o
i
+
u
ii
u+
u
-i u
- -++
p
+ p <0 + p <0
i 5 2sin(314t 30)A的电流
求(1)感抗XL;(2)线圈两端的电压u; (3)有功功率和无功功率。
3.3.3 电容元件的交流电路
1.电流与电压的关系
基本关系式: i C du
设:u
dt
2 U sin ω t
i
+
u
C
_
则:i C du 2 UC ω cos ω t 电流与电压
时值表达式不变,电路中的电流的
有效值及无功功率又如何?
解:(1) XL L 3140.1 31.4()
QL UI 2207 1540(var)
I UL 220 7(A) X L 31.4
(2)
i C du dt
U jXC I
相量图
I U
U
I I
U
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (参考方向) 关系
阻抗
电压、电流关系
功率
瞬时值
有效值 相量图 相量式 有功功率 无功功率
i
+
单一参数交流电路的分析计算
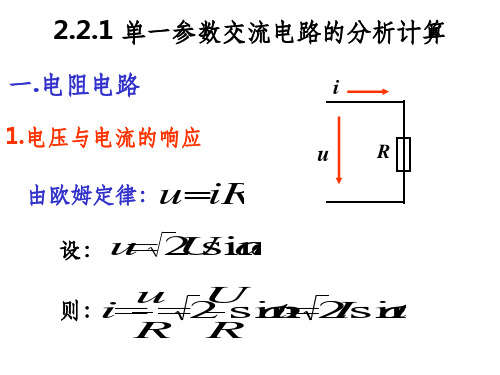
R uR
u L uL
C uC
流过各元件的电流相同。
各部分电压瞬时值服从基尔 霍夫电压定律。
uuRuLuCiR Ld dtiC 1idt
若:i 2Isint
u 2IR si nt 2I(L)sin t(90 0) 则: 2I(1c)sin t(90)
1. 相量方程式
U U RU LU C
设:i 2Isint 或 II0
j (XL-XC) :复数阻抗的虚部, 为电 抗。
注:Z 是一个复数,但不是一个正弦交流 相量( Z上不加 );Z 在方程式中只是 一个运算符号。
U IRjX LjX C ZRjXLXC
复数阻抗
Z R j(X L X C )R 2 (X L X C )2 t 1 g X L R X C Z
U
IL
I
4)相量关系式
设:II00
U U900 IL900
I
U IXLej900 I(jXL)
复数形式的
复感抗
欧姆定律
i
i 2Isint u 2Usi nt(900) u
2.电感电路中的功率
1)瞬时功率(p)
i
piuUsIi2n t
p
u t
电感元件的瞬时功率
随时间以 2变化。
能量转换过程可逆!
P >0 P <0 P >0 P <0
UC1滞后 I900 UC1=I XC1 U=滞1后00I450
I1
I
B UAB
I2
U10 20 10 2 01020
3、求解未知量,并将求得的结果转换成瞬时值 表达式。
串并联交流电路的计算
i
例1 分析:
C1 A u R i2 i1
u L uL
C uC
流过各元件的电流相同。
各部分电压瞬时值服从基尔 霍夫电压定律。
uuRuLuCiR Ld dtiC 1idt
若:i 2Isint
u 2IR si nt 2I(L)sin t(90 0) 则: 2I(1c)sin t(90)
1. 相量方程式
U U RU LU C
设:i 2Isint 或 II0
j (XL-XC) :复数阻抗的虚部, 为电 抗。
注:Z 是一个复数,但不是一个正弦交流 相量( Z上不加 );Z 在方程式中只是 一个运算符号。
U IRjX LjX C ZRjXLXC
复数阻抗
Z R j(X L X C )R 2 (X L X C )2 t 1 g X L R X C Z
U
IL
I
4)相量关系式
设:II00
U U900 IL900
I
U IXLej900 I(jXL)
复数形式的
复感抗
欧姆定律
i
i 2Isint u 2Usi nt(900) u
2.电感电路中的功率
1)瞬时功率(p)
i
piuUsIi2n t
p
u t
电感元件的瞬时功率
随时间以 2变化。
能量转换过程可逆!
P >0 P <0 P >0 P <0
UC1滞后 I900 UC1=I XC1 U=滞1后00I450
I1
I
B UAB
I2
U10 20 10 2 01020
3、求解未知量,并将求得的结果转换成瞬时值 表达式。
串并联交流电路的计算
i
例1 分析:
C1 A u R i2 i1
正弦交流电路的分析—RLC并联电路的分析

分析依据:补偿前后 P、U 不变(已知)。
IC
UC
U
P
cos1
sin 1
U
p
cos
sin
P U
(tan 1
tan )
U
C
P
U
2
(tan 1
tan )
1
I1
I
IC
功率因素的提高
✓ 课堂练习
例:已知一台单相电机接在220V、50Hz的交流电上,吸收1.4kW 的功率,功率因数为0.7,需并联多大的电容,才能将功率因数提高至 0.9?
I
R I2 U I1 jXL jXC
•
I2
••
=0 I U
1
•
•
I1
I2
并联谐振电路
✓ 并联谐振的条件
U IZ
I
R
1
jL
jC
U
R
2
R
L2
j
R2
L
L2
C U
实部
虚部
I
R I2 U I1 jXL jXC
•
I2
••
=0 I U
1
•
•
I1
I2
并联谐振电路
✓ 并联谐振的条件
I
R2
R
解: (已知P=1.4kW,U=220V,cos1=0.7,cos=0.9)
由题意可知: f=50Hz,=2f=100 rad/s
tan1=1,tan=0.5
C
P
U
2
(tan 1
tan )=46 F
功率因素的提高
✓ 小结
功率因数是衡量电气设备效率的参数; 提高功率因数的方法:并联合适电容器。 用并联电容器法提高功率因数时,若原电路的功率因数为cos1 ,补 偿后为cos ,补偿前后负载的P、U不变,则电容C为:
RLC电路

C C
ɺ ɺ ɺ ɺ U = I R + I (j X L ) + I ( − jX C ) 总电压与总电流 的相量关系式 ɺ = I [R + j( X − X )]
L C
ɺ ɺ 根据 U = I [R + j ( X L − X C )]
令 Z = R + j ( X L − XC ) 则 阻抗 复数形式的 欧姆定律
储能元件上 的瞬时功率
在每一瞬间, 在每一瞬间,电源提供的功率一部 分被耗能元件消耗掉, 分被耗能元件消耗掉,一部分与储能 元件进行能量交换。 元件进行能量交换。
(2) 平均功率P (有功功率) 平均功率P 有功功率)
1 T P = ∫ pdt T 0 1 T = ∫ [UI cosϕ − UI cos (2 ω t + ϕ )]d t T 0 单位: 单位 W = UI cosϕ cosϕ 称为功率 cosϕ
而是 (3)相量图 相量图
ɺ ɺ ɺ ɺ U = UR +UL +UC
ɺ ɺ UL +UC
(4) P = UI cosϕ = 220 × 4.4 × cos ( −53°)W
= 580.8W
或 P = U R I = I 2 R = 580.8W
ɺ UC
(4) Q = UI sinϕ = 220 × 4.4 × sin ( −53° )var
i = 4.4 2 sin ( 314 t + 73 °)A
(2)
50 X L − XC 40 - 80 ϕ = arctan = arctan = -53 ° R 30
Z
U R = IR = 4.4 × 30V = 132V
uR = 132 2 sin ( 314t + 73° )V
ɺ ɺ ɺ ɺ U = I R + I (j X L ) + I ( − jX C ) 总电压与总电流 的相量关系式 ɺ = I [R + j( X − X )]
L C
ɺ ɺ 根据 U = I [R + j ( X L − X C )]
令 Z = R + j ( X L − XC ) 则 阻抗 复数形式的 欧姆定律
储能元件上 的瞬时功率
在每一瞬间, 在每一瞬间,电源提供的功率一部 分被耗能元件消耗掉, 分被耗能元件消耗掉,一部分与储能 元件进行能量交换。 元件进行能量交换。
(2) 平均功率P (有功功率) 平均功率P 有功功率)
1 T P = ∫ pdt T 0 1 T = ∫ [UI cosϕ − UI cos (2 ω t + ϕ )]d t T 0 单位: 单位 W = UI cosϕ cosϕ 称为功率 cosϕ
而是 (3)相量图 相量图
ɺ ɺ ɺ ɺ U = UR +UL +UC
ɺ ɺ UL +UC
(4) P = UI cosϕ = 220 × 4.4 × cos ( −53°)W
= 580.8W
或 P = U R I = I 2 R = 580.8W
ɺ UC
(4) Q = UI sinϕ = 220 × 4.4 × sin ( −53° )var
i = 4.4 2 sin ( 314 t + 73 °)A
(2)
50 X L − XC 40 - 80 ϕ = arctan = arctan = -53 ° R 30
Z
U R = IR = 4.4 × 30V = 132V
uR = 132 2 sin ( 314t + 73° )V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Il IP U l 3 U P 30
三相交流电路的小结(4)--三相功率计算 三相总功率: P P 负载对称时:
A
PB PC
和接法 无关
P 3 U p I p cos
P 3 Ul Il cos
三相三线制接法,用二个功率表测功率(二瓦计法) :
A
iA
2
三相交流电路的小结(1)--三相电源
三相四线制 (Y形联接)
eC
eA
eB
A
N B C
三相电源 一般都是 对称的, 称三相对 称电源
三相三线制(Y形联接) A
eC
eA
三相三线制(Δ形联接) A
eC
eB
eA
B C
eB
B C
三相交流电路的小结(2)--三相负载
星形负载
A Z N B C Z A Z B C Z
U
I
u领先 i 90°
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2I sin t
I jX U L
0
UI I2XL
设
i
C
u
du j 1 则 iC C dt 1 i j c
无源单口网络功率 1)瞬时功率:
p(t ) u(t )i(t )
p(t ) 2U cos(t u ) 2I cos(t i )
UI cos(u i ) UI cos(2t u i )
UI cos UI cos(2t u i )
2、根据相量模型列出相量方程式或画相量图 300V ,阻抗Z为多大时取得最大功率, 七、已知 U S 最大功率为多少?(10分)
Z 50 j150
取得最大功率 最大功率的大小为
Pmax
5 2 100 50 0.25W
* W1
*
*
Z A uA
ZB
B
iB
iC
u AC
uBC
三角形负载
Z
Z
三相交流电路的小结(3)--三相电路计算
负载不对称时:各相电压、电流单独计算。 负载对称时:电压对称、电流对称,只需计算一相。
求电表读数时,可只算有效值,不算相位。
三相电路的计算要特别注意相位问题。 负载Y形接法 电源对称时: 负载形接法 对称负载下:
I l 3I P 30 U U l P
功率因数的提高
并联电容值的计算
i
R
P C ( tg tg ) L 2 U
uR
uL
u
C
L
(6)电路本身呈容性不能采用并联电容的 方法提高功率因数。
一般正弦交流电路的解题步骤
1、据原电路图画出相量模型图(电路结构不变)
R R 、 L jX L、 C jX C 、 i I、 e E u U
u 5 2 sin( t 126 9 )
I
阻抗三角形
电压三角形 功率三角形
U
Q S
R
U R
U
L C
U L
U C
Z
X L XC
R
U U L C
U R
P
(二)一般正弦交流电路的解题步骤
1、据原电路图画出相量模型图(电路结构不变)
R R 、 L jX L、 C jX C 、 i I、 e E u U
u 2U sin t
U 2 1
U IX C XC 1
I
UI
I jX U C
C sin(t 90)
C
U
u落后i 90°
0
I 2 XC
符号说明
瞬时值 --- 小写 有效值 --- 大写 最大值 --- 大写+下标
u、i
U、I
Um
复数、相量 --- 大写 + “.”
(恒定分量) (正弦分量:2)
2)平均功率:
1 P T
说明:
p(t )dt UI cos (W )
0
T
1) P = UI cos UI;
2) cos 称作功率因数;
3) —功率因数角 (无源单口网络: = Z):
4) P = P1 + P2 + P3…….;
5) P =I12R1 + I22 R2 + I32R3…….
U
提示
计算相量的相位角时,要注意所在 象限。如:
3 j4 U
u 5 2 sin( t 531 )
3 j4 U
3 j 4 U
3 j 4 U
u 5 2 sin( t 531 )
u 5 2 sin( t 126 9 )
3)无功功率:
Q UI sin (Var)
说明:
1) Q > 0 ( 感性);Q < 0 (容性): 2) Q = Q1 + Q2 + Q3…….:
3) Q = I12X1 + I22 X2 + I32X3…….;
4) 反映网络与电源能量交换最大速率。
4)视在功率: 定义: 计算:
S UI (VA)
2、根据相量模型列出相量方程式或画相量图 3、用复数符号法或相量图求解
4、将结果变换成要求的形式
正弦交流电路的功率问题
• 功率本身是标量,电路总的有功等于各个 元件有功功率之和,而不需去考虑电路中 各个元件的连接形式。 • 总的有功于所有电阻的有功功率之和 • 总的无功等于所有元件无功功率之和
正弦稳态电路功率
注意:S S1 + S2 + S3…….
1) S=UI 2 2 S P Q 2)
求取电路功率因数的问题
cos
对于任何无源二端网络总可通过电路的等效变换变为基本的 RLC串联电路
功率因数角是二端网络端口总电压与总电流的夹角
功率因数角可由电压三角形 阻抗三角形 功率三角形求出
由于功率标量的特性对于混联的电路用功率三角形来求取总的功 率因数往往更简单
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (正方向) 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
I R U
UI
0
i 2I sin t
设
u、 i 同相
