哈尔滨工业大学理论力学第七版第10章 动量定理
理论力学10—动量定理

p 2m1vC m1vC1 m2v A m2v B
B
m2 vB 2m1vC
C
C
C1 m1vC1 O t
m2 v A A
x
v A 2l sin t
vB cos(90 t ) vc cos(90 2t ) B c vB 2l cos t B
10.2
动量定理
F fN C f ( P sin 45 mg cos30 )
从而摩擦力为
0 0 tt 0 tt
动量定理积分形式应用时经常使用投影式:
tt
若作用于质点上的外力主矢恒等于零,则质点的动量守恒, 此即质点的动量守恒定律。 若作用于质点上的外力在某轴上投影的代数和恒等于零,则 质点的动量在该轴上的投影守恒,此即质点对轴的动量守恒 定律。
10.2
动量定理
y
例4 锤的质量m=3000 kg,从高度h=1.5 m 处自由下落到受锻压的工件上,工件发生变 形历时τ=0.01s ;求锤对工件的平均压力。 解:以锤为研究对象,和工件接触后受力如图。 工件反力是变力,在短暂时间迅速变化,用 平均反力N*表示。 锤自由下落时间
d ri vi dt
代入式10—1,注意到质量mi是不变的,则有
d ri d p mi vi mi mi ri dt dt i 1 i 1
令
M mi
n
n
为质点系的总质量
10.1
动量与冲量
m r m r i i i i rC mi M
1 p mvC ml 2
10.1
动量与冲量
vC C
理论力学课件-动量定理

vA
A D
C
p=
p +p
2 x
2 y
ω O
vE
φ E
1 = (5 1 +4m )lω m 2 2
方向余弦为为
vD
x
px c s( p x) = o , , p
co p y) = s( ,
py p
22
解法二: 解法二 整个机构的动量等于曲柄OA、规尺 、 整个机构的动量等于曲柄 、规尺BD、 滑块B 的动量的矢量和, 滑块 和D的动量的矢量和,即 的动量的矢量和
y vB B
vA
A D x
p = pOA + pBD + pB + pD
其中曲柄OA的动量 OA=m1vE ,大小是 其中曲柄 的动量p 的动量 大小是
ω O
vE
φ E
vD
y
pOA = m1vE = m1lω/2
其方向与v 一致,即垂直于OA并顺着 并顺着ω的转 其方向与 E一致,即垂直于 并顺着 的转 向(图 b) 图
31
质点系动量定理
p = ∑ mi vi
d(mvi ) d p i =∑ = d t d t
n
∑ma =∑F
i i i
n n d (mi vi ) = ∑ Fi (e ) + ∑ Fi (i ) ∑ dt i =1 i =1 i =1
∑F =0 i
(i)
dp (e) =∑ i F dt
质点系动量对时间的导数, 质点系动量对时间的导数,等于作用于它 上所有外力的矢量和,称为动量定理 动量定理。 上所有外力的矢量和,称为动量定理。
?
14
9.1 动量与冲量
理论力学第十章质心运动定理动量定理习题

yOyO第十章 质心运动定理 动量定理 习题解[习题10-1] 船A 、B 的重量别离为kN 4.2及kN 3.1,两船原处于静止间距m 6。
设船B 上有一人,重N 500,使劲拉动船A ,使两船靠拢。
若不计水的阻力,求当两船靠拢在一路时,船B 移动的距离。
解:以船A 、B 及人组成的物体系统为质点 系。
因为质点系在水平方向不受力。
即:0=∑ixF,设B 船向左移动了S 米, 则A 船向右移动了6-S 米。
由质点系的动量定理得:t v m m v m B B A A x F 0])([=--人+0])([=-人B B A A v m m v m + B B A A v m m v m )(人+= B B A A v m m v m )(人+=tsm m t s m B A)(6人+=- s m m s m B A )()6(人+=-s s )5.03.1()6(4.2+=-s s )5.03.1()6(4.2+=- s s 3)6(4=- )(43.3724m s ==[习题10-2] 电动机重1P ,放置在滑腻的水平面上,还有一匀质杆,长L 2,重2P ,一端与电动机机轴固结,并与机轴的轴线垂直,另一端则刚连一重3P 的物体,设机轴的角速度为ω(ω为常量),开始时杆处于铅垂位置而且系统静止。
试求电动机的水平运动。
rC 3C v →y解:以电动机、匀质杆和球组成的质点系为研究对象。
其受力与运动分析如图所示。
匀质杆作平面运动。
→→→+=1212C C C C v v v ωl v r C =212cos C x C v t l v -=ωω→→→+=1313C C C C v v v ωl v r C 23=13cos 2C x C v t l v -=ωω因为质点系在水平方向上不受力,所以0==∑ix x F F由动量定理得:t F v t l m v t l m v m x C C C =--+-+-0)]cos 2()cos ([111321ωωωω 00)]cos 2()cos ([111321=--+-+-C C C v t l m v t l m v m ωωωω 111132)cos 2()cos (C C C v m v t l m v t l m =-+-ωωωω 11113322cos 2cos C C C v m v m t l m v m t l m =-+-ωωωω 1)(cos 2cos 32132C v m m m t l m t l m ++=+ωωωωt m m m m m l v C ωωcos )(321321+++=At m m m m m l dtdx C ωωcos )(321321+++=tdt m m m m m l dx C ωωcos )(321321+++=tdt m m m m m l x C ωωcos )(321321⎰+++=)(cos )(321321t td m m m m m l x C ωω⎰+++=t m m m m m l x C ωsin )(321321+++=t P P P P P l x C ωsin )(321321+++=这就是电动机的水平运动方程。
理论力学(第七版)课后题答案哈工大

第1章 静力学公理和物体的受力分析
1-1 画出下列各图中物体 A,ABC 或构件 AB,AC 的受力图。未画重力的各物体的自 重不计,所有接触处均为光滑接触。
FN 1
A
P FN 2
(a)
(a1)
FT A P FN
(b)
A
(b1)
FN1
P
B FN 3
FR = (80i + 140 j ) N
FR = (80 N) 2 + (140 N) 2 = 161 N
2-2 如图 2-2a 所示,固定在墙壁上的圆环受 3 条绳索的拉力作用,力 F1 沿水平方向, 力 F3 沿铅直方向,力 F2 与水平线成 40°角。3 个力的大小分别为 F1=2 000 N,F2=2 500 N, F3=1 500 N。求 3 个力的合力。
C
FN 2
′ FN
B
P2
(a1)
FN1
(a) FN 1
B
C P2 FAy A
FN 2
FN
P1
P1
FAy
A F Ax
FAx
(a2)
(a3)
FN1
A P1 B P2
FN 3
FN 2
(b)
(b1)
′ FN
FN 1
A
B P2
FN 3
P1
FN
FN 2
(b3)
(b2)
3
理论力学(第七版)课后题答案 哈工大.高等教育出版社
F2 = 173 kN
如图 2-5a 所示,刚架的点 B 作用 1 水平力 F,刚架重量不计。求支座 A,D 的约
y F B C x
理论力学十动量定理
?
§10-1 动量和冲量
动量——表征物体机械运动强度的一种度量。 质点的动量 —— 质点的质量与质点速度的乘积, 称为质点的动量。
p m
质点系的动量——各质点动量的矢量和,称为质点
系的动量。
p m1 1 m2 2 mn n mi i
冲量——力在一段时间内的累积效应。
dp y P 2 r sin FN1 FN 2 FN 3 3Q P dt g
F
B D O2
P
φ
Q
FN2
t
1、FN 2和FN 3 为静压力,则 设 FN
D
DO
2
φ
D
1 FN 2 FN 3 3Q P 0 FN
1、约束反力 Fx Fx Fx , Fy Fy Fy 静约束反力 Fx 0, Fy m1 g m2 g 动约束反力 Fx m2e 2cost ;Fy m2e 2sin t 动约束反力的最大值
2 Fx m2e
Fy m2e 2
B D O2 φ
P
F
Q
FN2
§10-3 质心运动定理 设质点系由n个质点组成,其中第i个质点的质 量为 m i ,矢径为 ri ,则质点系的质量中心C的坐 标为 mi ri rC m 将上式对时间求两次导数
d rC m mC mii dt d C m m aC mi ai dt
2、电动机跳起的条件;
Fy m1 g m2 g m2 e 0
2
m1 g m2 g m2 e
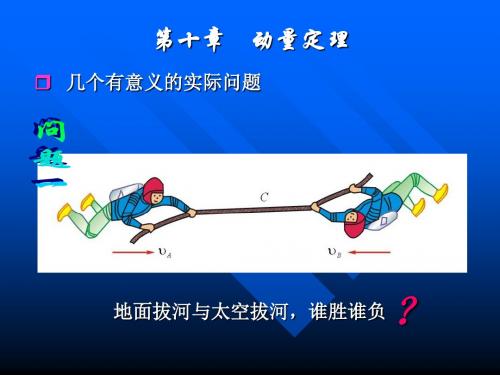
地面拔河与太空拔河,谁胜谁负
?
若以首先越过AB中点为负,那么质量大的宇航员胜。
第十章.动量定理(哈工大 理论力学课件)

§10-2 动量定理
二、冲量定理
p2 p1
t2 Fedt
I
t1
具体计算时,往往写成投影形式,即
p2x p1x
t2 t1
Fx
e
dt
Ix
p2 y p1y
t2 t1
F
y
e
dt
Iy
p2z p1z
1、如果在上式中
Fe
0,则有 p p0
常矢量
结论
其中:p0 为质点系初始瞬时的动量
在运动过程中,如作用于质点系的所有外力的矢量和始终等 于零,则质点系的动量保持不变。这就是质点系的动量守恒 定理
§10-2 动量定理
§10-2 动量定理
§10-2 动量定理
例10-2
例10-2:火炮(包括炮车与炮筒)的质量是 m1,炮弹的 质量是 m2,炮弹相对炮车的发射速度是 vr,炮筒对 水平面的仰角是α(图a)。设火炮放在光滑水平面上, 且炮筒与炮车相固连,试求火炮的后坐速度和炮弹的
§10-2 动量定理
一、动量定理
dp dt
Fe 质点系动量定理的微分形式
二、冲量定理
设在 t1 到 t2 过程中,质点系的动量由 p1 变为 p2,则对上式积
分,可得
p2 p1
t2 Fedt
t1
I
即,质点系的动量在一段时间内的变化量,等于作用于质点系 的外力在同一段时间内的冲量的矢量和,这就是质点系动量定 理的积分形式。常称为质点系的冲量定理。
t1
§10-1 动量与冲量
从起始点开始的冲量为:
t
I 0 Fdt
理论力学第十一章,动量定理

的投影守恒。
y
α
px px0
vr m2g v
vm1
vr
A
FA m1g
x
vm1
α
B
FB
(b)
(a)
α
vm1
m2g x
p mi v i
p x mi vix
A
FA m1g
B
FB
例 题1
v
考虑到初始瞬时系统处于平衡,即有pox=0,于是有 px = m2vcos m1vm1 = 0 另一方面,对于炮弹应用速度合成定理,可得 v = ve + vr 考虑到 ve = vm1,并将上式投影到轴 x 和 y 上,就得到 vcos = vrcos vm1
质点系冲量定理投影形式
e e p2 y p1 y ( Fiy ) dt I iy t2 t1 e p2 z p1 z ( Fize ) dt I iz t2 t1
dp Fie dt
dpx e Fix dt
3,质点系动量守恒定律
Fi e 0 , 1)
y
α
vr vm1
m2g x
A
FA m1g
B
FB
(a)
例 题1
解: 取火炮和炮弹(包括炸药)这个系统作为研究对象。
设火炮的反座速度是 vm1,炮弹的发射速度是 v,对水平面的仰 角是 (图b)。 炸药(其质量略去不计)的爆炸力是内力,作用在系统上的外力 在水平轴 x 的投影都是零,即有Fx = 0;可见,系统的动量在轴 x 上
(m1 m2 ) C Fy m1 g m2 g y
质心 C 的坐标为
理论力学动量定理PPT课件

dpx
dt
i
Fixe ,
dpy dt
i
Fiye ,
dpz dt
i
Fize
若作用在质点系上的外力主矢不恒为零,但在某个坐标轴上的 投影恒为零,由上式可知,质点系的动量在该坐标轴上守恒。例 如
FRex 0 , px C2
式中C2为常量,由运动初始条件决定。
第23页/共50页
第10章 动量定理 质心运动定理
第4页/共50页
几个有意义的实际问题
蹲在磅秤上的人站起来时, 磅秤指示数会 不会发生的变化?
?
第5页/共50页
几个有意义的实际问题
? 台式风扇放置在光滑的台面上的台式风扇工作时,
会发生什么现象?
第6页/共50页
几个有意义的实际问题
隔板
水池
? 抽去隔板后,将会
发生什么现象?
水
光滑台面
第7页/共50页
v
- m1cos m2
m1 m2 m3 m4
vr
第32页/共50页
动量定理应用举例 例 题 1
解:2. 确定四棱柱体的速度和四棱柱体 相对地面的位移。
v
- m1
m1cos m2
m2 m3 m4
vr
又因系统初始静止,故在水平方向上质心守恒。对上式积分, 得到四棱柱体的位移。
x - m1cos m2 s
m1 m2 m3 m4
第33页/共50页
动量定理应用举例 例 题 1
解:3.确定对凸起部分的作用力,可以 采用质心运动定理。
设物块相对四棱柱体的加速度为ar, 由于凸起部分的作用,四棱柱体不动,
ae a4 0 ar a 故,四棱柱体的加速度a极易由牛顿定律 求出。 根据质心运动定理,并注意到
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i
v
n
m
n
i
v
i
M
C
r V
C
r r p = MV
意义?
C
结论: 系统的动量大小 = 系统的质量与质心速度的乘积
∗ 均质圆轮重Q,半径R,求:动量p
A
O
Q
v C
C
B
p
ω
Q =MV c = Rω g
p =?
Q
O
ω
已知杆长L,重Q, A , ϕ;求:动量p v
A
K
p = MV
Q = V g
B
C
v
A
C
(e)
* 投影式:
Ma = M&& = ∑ F x Ma = M&& = ∑ F y
Cx C Cy C Cz C
( e)
x ( e)
y (e )
Ma = M&& = ∑ F z
* 两类问题:
dv M aC = M = ∑Fτ(e) dt 2 vC n M aC = M = ∑Fn(e)
t
ρ
z
Fb(e) = 0 ∑
a
t C
∑Fn = maC
n
∑F = ma
t
t C
= man = 0 Fox c t = P Lα − Foy + P = ma c 6g
六、质心运动守恒
(e)
r r ∑ 1.当: F = MaC ≡ 0
r V = 常矢
C
* 质心作何种运动 ?
∗若:V (0)= 0,
C
* 质心作何种运动 ?
质心坐标守恒!
ω
2
= Q − mat = Q − mRα Foy c
Q ω=0 ∴ a = 0 1 a = OC ⋅ α = 6 Lα
n
t
α 角速 度为0,角加速度为 ,求此时O的约束力 取杆: 受力分析 2L / 3 L/3 运动分析 FOx o C
A
C
均质杆在图示位置无初速地释放时,
P
α
B
C
F
Oy
据质心运动定理
1,已知质心运动,求外力 2,已知外力,求质心运动
—— 微分 —— 积分
∗ 均质圆轮重Q,半径R,求:O处的约束力
A
取轮:受力分析、运动分析
∑Fn = maC
n
F
Ox
O
a
n C
= man
∑F = ma
t
t C
ω
α
F
Oy
+ Q = mat −FOy c
a
t C
得:
= − man = −mR Fox c
运动分析
ϕ
∑F ≡ 0
(e) x
∴ p = 常量
x
动点:小棱柱 动系:大棱柱
a e
r r r V = V +V
r
v
e
F
N
ϕ
M (−v)+mvax =0
M (−v) + m(v cos ϕ − v) = 0 ve
r
F
N
ϕ
得:
( M + m)v = m cos ϕ v
t 0
S
r
( M + m ) ∫ vdt = m cos ϕ ∫ v dt
—— 积分形式
mv
2
* 投影式
d ( mv ) = F x x dt d ( mv ) = F y y dt d ( mv ) = F z z dt
* 思考:
mv2x − mv1x = I x = ∫ Fxdt
mv2 y − mv1y = I y = ∫ Fy dt mv2z − mv1z = I z = ∫ Fz dt
第十章 动量定理
* 普遍定理之一:
动 量 定 理
* 任务: 动量的改变与力之间的关系, 并研究动量定理的另一重要形式 —— 质心运动定理
一、动量 1,质点 矢量
r r p = mv
瞬时量 绝对量
m
r v
⋅ 单位: kg⋅m/s
v
2,质点系
1
r r p = ∑m v r r p = MV
i
C
m
m
1
V
C
C
Q
ϕ
V
B
ω
A
L
B
求:杆AB的动量
G
p = MV
C
v
C
?
ω
* 轮作纯滚动
O
•
vo
求:轮的动量
R
W
p = MV
O
W = Rω g
vA
求:系统的总动量
E
vr E v ω W
O
l
C
C
2W ϕ
B
vB
2W W + VB g VC g
W
W p= V g
+ E
V = V = V = 2V = rω
B C A E
o
ϕ
m
x
均质杆长2 L,初始铅垂静止,无初速倒下, 地面光滑,求:B点的运动轨迹
取杆
Q
y
∑F x = 0
且初始静止
B
∴xC = 常量
x
y
= L cosϕ B
B
= 2Lsin ϕ
2 2 B 2 B 2
C
x+ y L (2L)
=1
A
ϕ
P
O
x
F
A
B 点的轨迹为一椭圆
ϕ
∑F ≡ 0
(e) x
∴ p = 常量 = 0
x
又:初始静止
∴x = 常量
C
v
e
F
N
ϕ
设大棱柱右移 ∆x
y
质心位置线
* 下滑前
M x + mx x = M +m
A C1
B
ϕ
* 下滑后
xC2 =
M (x + ∆x) + m[ xB + ∆x + (a − b)]
A
M +m
x =x
C1
∆x
b
C2
m(a − b) ∆x = − M +m
t 0 r
∫ vdt = S
t 0
a −b ∫ v dt = cosϕ
t 0 r
m(a − b) ∴S = (M + m)
五、质心运动定理
r r(e) dp = ∑F dt
r r p = MV
C
r r ∑ F = M aC
(e)
质心运动定理 * 结论:内力不能改变质心的运动!
r r ∑ F = M aC
2.当: ∑F x = M
(e)
Cx C
a
Cx
≡0
& V = x = 常量
* 质心作何种运动?
∗若:V (0)= 0,
Cx
* 质心作何种运动?
质心坐标在x方向守恒!
3,守恒现象
* 力偶对物体的作用
M
C
物体的运动状态?
* 大棱柱质量M,小棱柱质量m,水平面光滑。 求:小棱柱滑到大棱柱底部时,大棱柱的位移 (设初始静止) 取系统 受力分析
t2 t1
—— 元冲量 —— 冲 量
r r I = ∫ F • dt
三、动量定理 1,质点 r r dv r Qma = m = F dt
v
1
r ∑F
m
mr
r a
v
r r r )=F dt d r ∴ (mv) = F d (m v dt
—— 微分形式
m
mv
v
I
2
1
r r −m r I = mv 2 v1
t1 t1 t2
t2
t1 t2
能否向自然轴系投影?
2,质点系 任取一质点 m i 应用微分形式:
(e) (i) i i
r r )= F dt + r dt d (mi v i F F r ) = ∑ r ( e ) dt + ∑ r (i ) dt ∑ d ( mi v i Fi Fi r
r r mi F
2x 1x 2y 1y 2z 1z
(e) x (e) y
(e) z
四、动量守恒
r dp 1,当: = dt
r ∑F
(e)
≡0
r p
2,当:
2
r = p = 常矢
1
—— 质系动量守恒
d
p
=
x
dt
2x
= ∑Fx ≡ 0
(e)
p
p
1x
= 常量
—— 质系动量在x方向守恒
* 大棱柱质量M,小棱柱质量m,水平面光滑。 求:小棱柱滑到大棱柱底部时,大棱柱的位移 (设初始静止) 取系统 受力分析
(i ) i
(e)
i
r r r dp = ∑F dt = ∑dI
( e)
r ( e) dp = ∑F dt
r r p − p = ∑I
2 1
—— 微分形式
(e)
—— 积分形式
* 投影式:
d d d
P
dt
x
= = =
∑F ∑F ∑F
(e) x
P
dt
y
(e) y (e) z
P
dt
z
P − P = ∑I P − P = ∑I − P = ∑I P
7W p= 2g
rω
求:系统的总动量
