排队论运筹学论文
排队论在超市的运用与分析学士学位论文

排队论在超市的运用与分析摘要近年来,大型超市不断的兴起给人们带来了许多便利。
但是由于种种原因大型超市的排队服务系统并不完善,常常出现了队列过长或者服务台空闲等问题,因此,优化大型超市排队服务系统,减短队列便有具有了重大意义。
本文针对沈阳乐购超市服务排队系统进行优化。
首先对排队论的相关知识进行介绍,对多服务窗等待制M/M/n/∞/∞排队模型进行了重点阐述。
其次对沈阳乐购超市浑南店顾客服务时间,到达时间等数据进行调查,取得原始数据代入排队模型进行实证分析,计算出了相应的目标参量,确定了该超市各个时段应该开放的最佳收银台的数量。
然后运用FLEXSIM对服务系统进行仿真以确定该优化方案是可行的。
在此基础上本文对乐购超市的收银通道,扫描,员工专业度等方面提出问题并对其优化,最后对超市的发展提出意见。
本文的研究成果对大型商场、医院、银行等具有收费服务系统的服务企业具有普遍的借鉴意义。
关键词:大型超市;排队服务系统;建模;仿真;优化AbstractIn recent years, the continuous rise of large supermarkets have brought a lot of convenience to peaple. However, due to various reasons, the large supermarket's queuing system is not perfect, many problems often arised, such as the queue is too long or deskes are idling. Therefore, to optimize the queuing service system of large supermarket to shorten the queue will have a great significance.This thesis aimed at to optimize the service queuing system of Shenyang Tesco Supermarket. At first, the knowledge about queuing theory has beed introduced, and the multi-window waiting for M/M/n/∞/∞queuing model has beed focused on. Secondly, a survey of customer service time, arrival time and other data has beed conducted at Shenyang Tesco supermarket Hunnan store. Then, the original data abtained from the survey has been put into the queuing model to conduct a empirical analysis. And as a result, the corresponding target parameters are calculated, and so to determine the number of cash register at various hours of the supermarket should beed opened. Next, by using the FLEXSIM service system to conduct a simulation, finding out the optimization is feasible. On this basis, this thesis discussed the problem of cashier channel, scanning equipment and staff professionalism of the Tesco supermarket,and optimizing these problem at the same time.Finally, this thesis has give some advices about how to development the supermarket.The results of this paper have universal referenceto for large shopping malls, hospitals, banks and other service enterprises who have the fee-based services systems.Keywords: supermarkets; queuing service system; modeling; simulation; optimization目录摘要 (I)Abstract (II)目录 ........................................................................................................................................ I II 1 绪论 .. (1)1.1 课题研究的背景及意义 (1)1.2 国内外研究现状 (1)1.3论文的主要研究内容及组织结构 (4)1.3.1论文主要研究内容 (4)1.3.2 论文主要组织结构 (4)2 超市排队服务系统相关理论知识 (5)2.1 排队论 (5)2.1.1 排队论的概念与发展 (5)2.1.2 排队论研究的内容 (6)2.2 排队系统 (7)2.2.1 排队系统的组成 (7)2.2.2 排队系统的主要指标 (9)2.2.3排队系统的最优化 (10)2.3 排队系统的建模 (12)2.3.1系统建模的要求 (12)2.3.2系统建模的原则 (12)2.3.3系统建模的方法 (13)2.3.4系统建模的步骤 (13)2.3.5排队系统建模的符号与分类 (14)2.3.6 M/M/n/∞/∞模型 (14)2.4 排队系统的仿真 (15)2.4.1 离散事件系统仿真 (15)2.4.2 FLEXSIM软件的介绍 (16)3 服务系统数据采集与指标计算 (17)3.1 沈阳乐购超市周边环境描述 (17)3.2 数据采集 (17)3.2.1 顾客到达时间服从分布的研究 (20)3.2.2 顾客服务时间服从分布的研究 (23)3.3 系统指标计算及优化 (25)3.3.1 超市收银服务系统应用排队模型 (25)3.3.2 系统指标计算 (26)3.4 大型超市各时段最优服务台数确定 (27)4 顾客排队状况的计算机仿真 (31)4.1 排队服务系统模型假设 (31)4.2 顾客排队状况的计算机仿真 (32)4.3 超市排队服务系统的主要参数技术指标结果分析 (37)5 大型超市服务工作优化设计 (40)5.1 现有超市收银服务工作 (40)5.2 超市收银通道优化 (41)5.3 超市商品扫描结算工作优化 (43)5.4 员工专业度的改进 (45)5.4 对超市发展的建议 (45)结论 (46)致谢 (47)参考文献 (48)附录A (50)附录B (58)1 绪论1.1 课题研究的背景及意义排队服务系统在人们实际生产生活中应用十分广泛,如顾客到超市付款,病人在医院排队看病,此外,计算机网络中数据的存储转发、电话机的占线问题、交通枢纽的车船堵塞和疏导、水库的存储调节等等都是排队现象。
运筹学排队论2

换为 t ,得到
pn
(t)
(t)n
n!
et
,
t
0,
n
0,1,2,.
表示长为t的时间区间内到达n个顾客的概率为 pn (t) ,且服从泊松分布.这称为泊松流或泊松过 程或简单流. 设t时间内到达的顾客数为随机变量N(t),则有
E[N(t)] t, D[N(t)] t.
服务台
2.C个服务台,一个公共队伍
服务台1 服务台2 服务台C
3.C个服务台,C个队伍
服务台1 服务台2 服务台C
二.排队系统的三个组成部分
1.输入过程:指顾客按怎样的规律到达. ⑴顾客的总体数或顾客源:指可能到达服务机
构的顾客总数.顾客总体数可以是有限的,也可 以是无限的; ⑵顾客到达的类型:顾客是单个到达还是成批 到达; ⑶顾客相继到达时间间隔的分布,如按泊松 分布,定长分布还是负指数分布.
排队论的创始人是丹麦哥本哈根市电话局的 工程师爱尔朗(A.K.Erlang),他早期研究电话 理论,特别是电话的占线问题,就是早期排队 论的内容.
§2 排队论的基本概念
一.排队现象的共同特征:为了获得某种服务而 到达的顾客,如不能立即得到服务而又允许排 队等候,则加入等待的队伍,获得服务后离开.我 们把包含这些特征的系统称为排队系统. 排队系统的几种情况: 1.单服务台排队系统
例9.1 某仓库全天都可以进行发料业务,假设 顾客到达的时间间隔服从均值为1的负指数分 布现在有一位顾客正好中午12:00到达领料, 试求:
(1)下一个顾客将在下午1:00前到达的概率; (2)在下午1:00与2:00之间到达的概率: (3)在下午2:00以后到达的概率。
运筹学排队论

降低平均服务时间
降低服务时间旳可变性
增长服务人员
降低平均到达人数
经过顾客预约等方法来降低到达旳可变性
集中使用服务资源
更加好地计划和调度
23
处理排队问题旳措施
2.其他措施
服务场合提供娱乐设施
医生等待室放报纸杂志
自动维修间用收音机或电视
航空企业提供空中电影
等待电梯处放镜子
超级市场把冲动性商品摆放在收款台附
排队论
1
2
•
排队论,又称随机服务系统理论(,是一
门研究拥挤现象(排队、等待)旳科学。详细
地说,它是在研究多种排队系统概率规律性
旳基础上,处理相应排队系统旳最优设计和
最优控制问题。
•排队论是1923年由丹麦工程师爱尔朗
(A.K.Erlang)在研究电活系统时创建旳.
3
案例-1 银行排队系统
4
案例-2 医院排队系统
用更快旳服务人员、机器或采用不同旳设施布局和政
策来影响顾客旳到达时间和服务时间。
9
1 排队论旳基本问题
1.1 排队论旳主要研究内容
• 数量指标
– 研究主要数量指标在瞬时或平稳状态下旳
概率分布及其数字特征,了解系统旳基本
运营特征。
• 统计推断
– 检验系统是否到达平稳状态;检验顾客到
达间隔旳独立性;拟定服务时间分布及参
数。
• 系统优化
– 系统旳最优设计和最优运营问题。
10
1.2排队论旳经济含义
• 排队问题旳关键问题实际上就是对不同
原因做权衡决策。管理者必须衡量为提
供更快捷旳服务(如更多旳车道、额外
旳降落跑道、更多旳收银台)而增长旳
排队论运筹学论文【范本模板】

排队论摘要:医院就医排队是一种经常遇见的非常熟悉的现象.它每天以这样或那样的形式出现在我们面前。
例如,患者到医院就医,患者到药房配药、患者到输液室输液等,往往需要排队等待接受某种服务.这里,护士台、收费窗口、输液护士台及其服务人员都是服务机构或服务设备。
而患者与商店的患者一样,统称为患者.以上排队都是有形的,还有些排队是无形的.由于患者到达的随机性,所以排队现象是不可避免的。
如果医院增添服务人员和设备,就要增加投资或发生空闲浪费;如果减少服务设备,排队等待时间太长,对患者和社会都会带来不良影响。
因此,医院管理人员要考虑如何在这两者之间取得平衡,以便提高服务质量,降低服务费用.所谓排队系统模拟建模,就是利用计算机对一个客观复杂的排队系统的结构和行为进行动态模拟,以获得反映其系统本质特征的数量指标结果,进而预测、分析或评价该系统的行为效果,为决策者提供决策依据。
关键字: 随机性,排队系统,动态模拟正文:排队系统的基本结构由四个部分构成:来到过程(输入)、服务时间、服务窗口和排队规则。
简单的排队系统的服务时间往往服从负指数分布,即每位患者接受服务的时间是独立同分布的,本文用泊松输入,建立模型.泊松输入即满足以下4个条件的输入:(1)、来到过程(输入)是指不同类型的患者按照各种规律来到医院。
(2)、服务时间是指患者接收服务的时间规律.(3)、服务窗口则表明可开放多少服务窗口来接纳患者。
(4)、排队规则确定到达的患者按照某种一定的次序接受服务.患者的总体可以是无限的也可以是有限的;患者到来方式可以是单个的,也可以是成批的;相继到达的间隔时间可以是确定的,也可是随机的;患者的到达可以是相互独立的,也可以是关联;到来的过程可以是平稳的,也可是非平稳的;患者接受服务的时间规律往往也是通过概率分布描述的。
常见的服务时间分布有定长分布、负指数分布和埃尔朗分布.一般来说,简单的排队系统的服务时间往往服从负指数分布,即每位患者接受服务的时间是独立同分布的,其分布函数为B ( t )= 1— e —m t (t ≥0).1其中m>0为一常数,代表单位时间的平均服务率. 而1/m 则是平均服务时间。
运筹学课排队论应用教学观察

运筹学课排队论应用教学观察运筹学是一门应用数学学科,旨在寻求最优解决问题的方法与技巧。
在运筹学中,排队论是其中的一个重要分支,它涉及到排队系统中的效率、等待时间以及资源利用率等方面的问题。
近年来,越来越多的学校引入运筹学课程,并将排队论应用于教学中。
本文将对运筹学课排队论应用于教学的观察进行分析和讨论。
一、排队论的基本概念与模型在介绍运筹学课排队论的应用之前,我们先对排队论的基本概念与模型进行简要介绍。
排队论主要研究排队系统中的各种性能指标,如队长、等待时间、服务效率等。
其中,常见的模型包括单队列模型、多队列模型以及网络模型等。
二、运筹学课排队论应用的教学观察运筹学课排队论的应用教学观察可以从以下几个方面进行观察:1. 培养学生问题分析与解决能力通过运筹学课排队论的应用教学,学生需要掌握排队系统的建模与求解方法。
这要求学生具备较强的问题分析与解决能力,能够将实际问题抽象成数学模型,并运用排队论的知识进行分析和求解。
2. 增强学生的团队合作与协作能力在排队论应用教学中,学生通常需组成小组共同完成课程设计或实践项目。
这要求学生加强团队合作与协作能力,每个小组成员需要分工合作、协调资源,共同解决排队系统中的实际问题。
3. 提高学生的数学建模能力运筹学课排队论的应用教学要求学生具备较强的数学建模能力。
学生需要将实际中的问题转化为数学模型,并通过数学方法进行求解。
这对于学生的数学思维能力、抽象建模能力以及数学工具的熟练程度提出了较高的要求。
4. 增加学生对实际问题的理解与应用能力运筹学课排队论的应用教学将数学理论与实际问题相结合,帮助学生更好地理解与应用数学知识。
通过实际问题的分析与解决,学生能够更好地理解排队论的概念与模型,并将其应用于实际情境中。
5. 培养学生的动手实践能力在运筹学课排队论的应用教学中,学生通常需要进行实践性项目,如实地观察与数据采集、模型构建与求解等。
这有助于培养学生的动手实践能力,提升他们在实际问题中的应用能力。
运筹学 排队论(1)

运筹学排队论1. 简介排队论是运筹学中重要的一个分支,它研究了在人员、物品或信息流动过程中产生的排队现象,并通过建立数学模型和分析这些模型来探讨和优化系统中的排队行为。
排队论在各个领域都有广泛的应用,如交通运输、电信网络、生产制造等。
2. 排队模型排队论中常用的模型包括M/M/1模型、M/M/s模型、M/G/1模型等。
其中,M表示到达过程的分布,而G表示服务时间的分布。
而数字1或s则表示系统中的服务通道数。
2.1 M/M/1模型M/M/1模型是排队论中最简单的一个模型,它假设到达过程和服务时间都服从指数分布。
该模型中只有一个服务通道。
2.2 M/M/s模型M/M/s模型是M/M/1模型的扩展,它假设到达过程和服务时间仍然服从指数分布,但有s个服务通道。
M/M/s模型适用于有多个并行服务通道的排队系统。
2.3 M/G/1模型M/G/1模型假设到达过程服从泊松分布,而服务时间服从一般分布。
该模型在实际应用中更为常见,因为服务时间往往不服从指数分布。
3. 排队论的性能度量排队论的性能度量是对排队模型进行定量分析和评估的重要手段,常见的性能度量指标包括平均等待时间、平均逗留时间、系统繁忙率等。
3.1 平均等待时间平均等待时间是指在排队系统中,每个顾客平均等待的时间长度。
通过对排队模型的分析和计算,可以得到平均等待时间的具体数值。
3.2 平均逗留时间平均逗留时间是指每个顾客在排队系统中逗留的平均时间长度。
它等于平均等待时间加上服务时间。
3.3 系统繁忙率系统繁忙率是指服务通道在单位时间内处于工作状态的比例。
它可以用来评估系统是否能够满足顾客的需求。
4. 排队论的应用4.1 交通运输排队论在交通运输领域的应用非常广泛。
例如,交通信号灯的控制就可以通过排队论进行优化,以减少车辆的等待时间和交通拥堵。
4.2 电信网络在电信网络中,排队论被用于研究数据包的传输和路由机制。
通过对排队论模型的分析,可以提高网络的传输效率和质量。
运筹学 排队论

S个服务台,一个队列的排队系统
排队系统类型:
服务台1
顾客到达 服务完成后离开
服务台2 服务台s
服务完成后离开
服务完成后离开
S个服务台, S个队列的排队系统
排队系统类型:顾客到达来自服务台1服务台s
离开
多服务台串联排队系统
排队系统类型:
聚 (输入)
服务机构
散 (输出)
随机聚散服务系统
随机性——顾客到达情况与顾客 接受服务的时间是随机的。 一般来说,排队论所研究的排队 系统中,顾客相继到达时间间隔 和服务时间这两个量中至少有一 个是随机的,因此,排队论又称 随机服务理论。
列车在系统中的平均停留时间
W=L/= 2/2=1(小时)
系统中等待编组的列车平均数
Lq=L-= 2-2/3=4/3(列) 列车在系统中的平均等待编组时间
Wq = Lq/ =(4/3)/(1/2)=2/3(小时)
记列车平均延误(由于站内2股道均 被占用而不能进站)时间为W0 则W0 = WP{N>2}=W{1-P0-P1-P2}
n:当系统处于状态n 时,整个系统的 平均服务率(单位时间内可以服务完 的平均顾客数);
当n为常数时记为;当每个服 务台的平均服务率为常数时,记每个 服务台的服务率为,则当n s 时, 有n=s。因此,顾客相继到达的平 均时间间隔为1/ ,平均服务时间为 1/ ,令= / s,则为系统的服 务强度。
W=E(T) :顾客在系统中的平均逗
留时间;
Tq:顾客在系统中的排队等待时间; Wq=E(Tq):顾客在系统中的平均
排队等待时间。
排队论研究的基本问题:
通过研究主要数量指标在瞬时或平稳 状态下的概率分布及数字特征,了解 系统运行的基本特征。 统计推断问题:建立适当的排队模型 是排队论研究的第一步,建立模型过 程中,系统是否达到平稳状态的检验; 顾客相继到达时间间隔相互独立性的 检验,服务时间的分布及有关参数的 确定等。
排队论论文【范本模板】
摘要:本文首先对排队论中的基本建模与相关知识点进行了总结,然后对生活中排队论的运用的例子进行了讲解,接下来对无线通信中排队论的运用进行了相关的说明。
最后进行了总结。
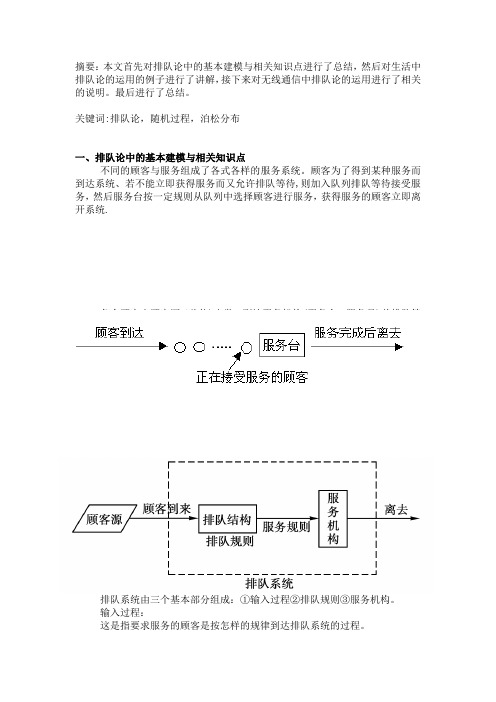
关键词:排队论,随机过程,泊松分布一、排队论中的基本建模与相关知识点不同的顾客与服务组成了各式各样的服务系统。
顾客为了得到某种服务而到达系统、若不能立即获得服务而又允许排队等待,则加入队列排队等待接受服务,然后服务台按一定规则从队列中选择顾客进行服务,获得服务的顾客立即离开系统.各个顾客由顾客源(总体)出发,到达服务机构(服务台、服务员)前排队等候接受服务,服务完成后离开。
排队结构指队列的数目和排列方式,排队规则和服务规则是说明顾客在排队系统中按怎样的规则、次序接受服务的。
排队过程的一般模型实际的排队系统虽然千差万别,但是它们有以下的共同特征:(1)有请求服务的人或物—-顾客;(2)有为顾客服务的人或物,即服务员或服务台;(3)顾客到达系统的时刻是随机的,为每一位顾客提供服务的时间是随机的,因而整个排队系统的状态也是随机的。
排队系统的这种随机性造成某个阶段顾客排队较长,而另外一些时候服务员(台)又空闲无事。
排队系统由三个基本部分组成:①输入过程②排队规则③服务机构。
输入过程:这是指要求服务的顾客是按怎样的规律到达排队系统的过程。
(1)顾客总体数,又称顾客源、输入源。
这是指顾客的来源。
顾客源可以是有限的,也可以是无限的。
(2)顾客到达方式。
这是描述顾客是怎样来到系统的,他们是单个到达,还是成批到达。
(3)顾客流的概率分布,或称相继顾客到达的时间间隔的分布。
顾客流的概率分布一般有定长分布、二项分布、泊松流(最简单流)、爱尔朗分布等若干种。
服务规则:(1)损失制。
这是指如果顾客到达排队系统时,所有服务台都已被先来的顾客占用,那么他们就自动离开系统永不再来。
(2)等待制。
这是指当顾客来到系统时,所有服务台都不空,顾客加入排队行列等待服务。
①先到先服务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排队论摘要:医院就医排队是一种经常遇见的非常熟悉的现象.它每天以这样或那样的形式出现在我们面前. 例如,患者到医院就医,患者到药房配药、患者到输液室输液等,往往需要排队等待接受某种服务.这里,护士台、收费窗口、输液护士台及其服务人员都是服务机构或服务设备.而患者与商店的患者一样, 统称为患者.以上排队都是有形的,还有些排队是无形的.由于患者到达的随机性,所以排队现象是不可避免的.如果医院增添服务人员和设备,就要增加投资或发生空闲浪费;如果减少服务设备,排队等待时间太长,对患者和社会都会带来不良影响. 因此,医院管理人员要考虑如何在这两者之间取得平衡,以便提高服务质量,降低服务费用.所谓排队系统模拟建模,就是利用计算机对一个客观复杂的排队系统的结构和行为进行动态模拟,以获得反映其系统本质特征的数量指标结果,进而预测、分析或评价该系统的行为效果,为决策者提供决策依据.关键字:随机性,排队系统,动态模拟正文:排队系统的基本结构由四个部分构成:来到过程(输入)、服务时间、服务窗口和排队规则.简单的排队系统的服务时间往往服从负指数分布, 即每位患者接受服务的时间是独立同分布的,本文用泊松输入,建立模型。
泊松输入即满足以下4个条件的输入:(1)、来到过程(输入)是指不同类型的患者按照各种规律来到医院.(2)、服务时间是指患者接收服务的时间规律.(3)、服务窗口则表明可开放多少服务窗口来接纳患者.(4)、排队规则确定到达的患者按照某种一定的次序接受服务.患者的总体可以是无限的也可以是有限的;患者到来方式可以是单个的,也可以是成批的;相继到达的间隔时间可以是确定的,也可是随机的;患者的到达可以是相互独立的,也可以是关联;到来的过程可以是平稳的,也可是非平稳的;患者接受服务的时间规律往往也是通过概率分布描述的. 常见的服务时间分布有定长分布、负指数分布和埃尔朗分布.一般来说, 简单的排队系统的服务时间往往服从负指数分布, 即每位患者接受服务的时间是独立同分布的, 其分布函数为B ( t ) = 1- e - m t (t ≥0).其中m>0为一常数, 代表单位时间的平均服务率. 而1/m 则是平均服务时间.服务窗口的主要属性是服务台的个数. 其类型有:单服务台、多服务台.多服务台又分并联、串联和混合型三种. 最基本的类型为多服务台并联.分为三类:损失制、等待制、混合制.损失制:患者到达时,如果所有服务台都没有空闲,该患者不愿等待,就随即从系统消失.等待制:患者到达时,如果所有服务台都没有空闲,他们就排队等待. 等待服务的次序又有各种不同的规则:①先到先服务,如就诊、排队取药等;②后到先服务,如医院处理急症病人;③随机服务, 服务台空闲时,随机挑选等待的患者进行服务;④优先权服务,如照顾号.混合制:既有等待又有损失的情况,如患者等待时考虑排队的队长、等待时间的长短等因素而决定去留.队列的数目可是单列,也可是多列的; 容量可能是有限的,也可能是无限的排队系统模型主要可以由输入过程(患者到达时间间隔分布)、服务时间分布、服务台个数特征来描述.根据这些特征,可用符号进行分类, 用以表示不同的模型. 例如,利用一定的符号规则将上述特征按顺序用符号列出,并用竖线隔开,即输入过程 | 服务分布 | 服务台个数例如, M|M|S 表示输入过程为泊松输入、服务时间服从负指数分布、S 个服务台的排队系统模型; M|G|1则表示泊松输入、一般服务分布、单个服务台的排队系统.评价和优化排队系统,需要通过一定的数量指标来反映.排队系统的主要数量指标 :建立排队系统模型的主要数量指标有三个:等待时间、忙期与队长.⑴ 等待时间 指患者从到达系统时起到开始接受服务时止这一段时间. 显然患者希望等待时间越短越好.用Wq 表示患者在系统中的平均等待时间.若考虑到服务时间,则用Ws 表示患者在系统中的平均逗留时间(包括等待时间和服务时间).该指标反映服务台的工作强度和利用程度.用B 表示忙期的平均长度.与忙期相应的是闲期,闲期是指服务台一直空闲的时间长度.用I 表示闲期的平均长度.⑶ 队长 指系统中的患者数(包括排队等候的和正在接受服务的所有患者).用Ls 表示平均队长.若不考虑接受服务的患者, 则将系统中排队等候的患者数称为队列长.用Lq 表示平均队列长.此外, 用r 表示服务强度,其值为有效的平均到达率l 与平均服务率m 之比, 即r =l/m . M | M | 1 模型M|M|1模型是输入过程为泊松输入,服务时间为负指数分布并具有单服务台的等待制排队系统模型,这是最简单的排队系统模型.假定系统的患者源和容量都是无限的,患者单队排列,排队规则是先到先服务.设在任意时刻t 系统中有n 个患者的概率Pn(t). 当系统达到稳定状态后,Pn(t)趋于平衡Pn 且与t 无关. 此时,称系统处于统计平衡状态,并称Pn 为统计平衡状态下的稳态概率. Pn=(1- r )r n, n = 0, 1, 2, … .其中r =l/m 表示有效的平均到达率l 与平均服务率m 之比(0<r <1).M | M | 1 模型的几个主要指标⑴ 在系统中的平均患者数(平均队长)Ls⑵ 在队列中等待的平均患者数(平均队列长)Lq⑶ 患者在系统中平均逗留时间Ws⑷ 患者在队列中平均等待时间Wq⑸ 闲期的平均长度I⑹ 忙期的平均长度B通过上述分析,各公式如下:s q L L λμ=+,,q s q s L L W W λλ==,2()s L ρλλμλμμλ==--,从其中的计算可知,等待时间,逗留时间,闲期的平均长度,忙期的平均长度等。
不同的服务规则,(先到先服务,后到先服务,随即服务),他们的不同点主要反映在等待时间的分布函数的不同,而一些期望是相同的。
上面讨论的这些指标,因为都是期望值,所以这些指标的计算公式对这三种服务规则都试用。
但对有优先权的规则不适用。
排队论有几个性能指标: 系统中的平均排队长度 Lq ;顾客在系统中的平均等待时间 Wq ; 顾客在系统中的平均逗留时间 WS ; 系统中的平均顾客数 LS 。
几个常用的数量指标 : 平均到达率λ; 平均服务率μ; 系统中并联服务台的数目 S ; 服务台强度 , 即每个服务台单位时间间隔内的平均服务时间ρ; 系统的稳态概率 P0 和繁忙概率 P 。
排队论中的排队模型有四种模型 ,银行营业网点适合于模型一的特征 ,也就是说:排队结构是单通道的 ,服务阶段单一 ,顾客总体是无限的 ,顾客到达的分布符合泊松分布 ,排队的规则符合先来的先服务 ,服务时间分布符合指数分布 ,队列的长度是无限的。
在一般情况下 , 银行要提高服务水平会降低顾客的等待成本 , 但这样通常会增加银行的成本。
我们的目标就是使二者的费用之和最小 ,从而达到最优化服务水平。
一般情形 ,银行服务费用是可以确切计算或估计的。
顾客的等待成本也是可以得到的。
比如 ,前面提到的三类服务系统可以帮助我们统计并解决这个问题 ;服务水平 ,一般用平均服务率来表示。
排队论的经济实质 :服务成本 =等待成本 ,即 Min (服务总成本)2 各种成本费用函数曲线的实质含义就是服务成本等于等待成本时 ,服务的总成本费用最小 ,同时也达到了最佳的服务能力。
运用排队论的相关知识 ,对于排队问题 ,我们有如下一些建议:确定一个可为顾客接受的等待时间 ; 在顾客等待过程中尽量分散其注意力 ;及时告诉顾客其期望了解的情况 ; 、决不能让顾客看到雇员并未工作;对顾客进行识别分类;对服务员进行应对排队问题的培训;鼓励顾客在非高峰期到达;制定消除排队的长期计划。
根据以上的知识和建议 ,下面我们寻找中国各大银行排队问题的根源以及相应的解决措施。
银行排队问题的根源国内金融服务供给总体不足,且呈现结构性矛盾,银行客户排队现象由来已久。
究其原因,一是由于银行网点及自助设备不足,民众办理业务往往只能求助柜台服务;二是银行效率不高,民众使用自助服务系统的习惯亦未养成。
具体表现在以下几个方面:(一) 银行承担大量代收代缴职能近年银行普遍承担了大量各类公共事业费用代收代缴职能,各类代收代缴业务品种及数量暴增,而各公共事业单位的系统接口、数据要求、发票格式等千差万别,造成银行电子渠道系统开发改造困难,业务无法大规模迁移至电子渠道进行,客户柜台拥挤严重。
(二) 居民理财需求迅速增长近年来,银行的个人金融产品和金融衍生产品不断推出,客户量激增。
客户大量增加,而银行网点受营运成本等因素制约,总量上基本保持不变,不同程度上造成了银行网点排长队的现象。
自去年以来股市不断升温,由此产生柜面受理基金开户、银证转账开户成倍增加。
以前办理一笔业务可能只需要2 分钟,但现在仅客户向银行柜员进行新产品咨询和沟通的时间可能就会达到10 分钟。
(三) 网点布局不够合理银行业协会在调研中发现,业务量较大的地区主要集中在经济发展热点地区、繁华商业区、大型居民社区、大型批发市场周边以及新建的、配套设施不完善的地区,这些地区由于银行网点相对偏少,服务半径过大,不能充分满足金融服务需求。
同时,部分银行柜面开工率较低。
比如有的网点共有14 个窗口,但仅开放6 个,开工率仅为42. 86 % 。
(四) 自助渠道利用率不高近年来,各银行不断加大自助设备投入,ATM、电话银行、网上银行的种类和数量日益丰富。
由于客户办理业务传统习惯和银行自身宣传力度不够,客户不了解、不信任或不习惯电子化服务,仍选择传统的柜台服务,致使自助设备、电子银行渠道使用率不高,难以缓解柜面压力。
(五) 业务办理环节增加由于近年银行案件频发,为防范各类风险,银行和监管部门对特殊业务的处理增加了许多风险控制环节,业务处理流程有些繁琐和复杂,致使每笔业务的平均处理时间过长,因此客户的等候时间也必然会更长。
(六) 大堂经理未能充分发挥作用调研中发现部分银行大堂经理配备不足。
如某银行北京分行储蓄所均未配备专职大堂经理,因而在高峰时段根本无法对客户进行分流。
此外,大堂经理职责定位不准。
目前,部分银行推行全员营销策略,大堂经理承担了诸如基金等业务的营销任务,影响了疏导客流功能的发挥。
(七) 客户金融知识有待加强调研发现,大多数储户存款时宁愿多花一些时间去储蓄网点柜台排长队,将现金亲自交到银行柜员手中,也不愿意尝试自助设备。
客户”不放心、怕吃亏”等顾虑成为银行推广自助设备的最大障碍。
根据中国银行业协会调查的结果,排队现象严重的其他原因,还包括风险防范力度加大从而造成业务办理环节增加,老年人对自助系统和电子渠道知识的匮乏,银行工作人员的工作态度以及工作熟练度等其他方面的原因。
参考文献[1] 高等学校试用教材.运筹学(第三版).北京:清华大学出版社,2008[2] 郭耀煌.运筹学原理与方法. 西南交通大学出版社,1994。
